Nell'ultima nostra chiacchierata sulle superfici di rotazione, che potete rileggere QUI, ci eravamo lasciati con l'intesa che nella successiva avremmo fatto la conoscenza di una superficie di rotazione che ricorda tanto una ciambella. Eccoci , dunque, qui a parlare del "toro" o "toroide". Ve lo presento subito nella sua veste grafica:

 

Appare, effettivamente, simile ad una ciambella, di quelle riuscite con il buco  ;-)

Poiché l'argomento del nostro studio è quello delle superfici di rotazione e l'obiettivo è ricavare la loro rappresentazione analitica (equazione) , vediamo di ricavare quella del toro.

Esso è generato dalla rotazione di una circonferenza attorno ad un asse appartenente al piano della circonferenza. Ma perché la ciambella riesca con il buco, è necessario che la distanza R tra l'asse di rotazione e il centro della circonferenza generatrice sia maggiore del raggio r di quest'ultima. Vediamo, infatti, per ora solo graficamente, cosa succede quando tale distanza varia tra zero ed r e quando , invece, è maggiore di r. Ho preparato la seguente animazione che illustra la metamorfosi della superficie di rotazione al variare della distanza del centro della circonferenza generatrice (di colore verde) dall'asse di rotazione (di colore blu). Durante la metamorfosi ho fatto continuare a ruotare la circonferenza generatrice attorno all'asse di rotazione.

 

Per R=0, ossia quando il centro della circonferenza generatrice giace proprio sull'asse di rotazione, il toro degenera nella sfera visibile all'inizio dell'animazione. Man mano che la distanza del centro della circonferenza verde dall'asse blu aumenta, la sfera si trasforma in una superficie di rotazione i cui due poli, superiore e inferiore, si avvicinano tra loro. In questo intervallo, la superficie di rotazione presenta una parte interna contenuta in quella esterna (visibile come leggermente più scura nella suddetta animazione). Per R=r, ossia quando la distanza del centro della circonferenza verde dall'asse blu coincide con il raggio della circonferenza stessa, i due suddetti poli vanno a coincidere tra loro. Per R>r, infine, ecco formarsi il "buco" della nostra ciambella.

 

Equazione cartesiana del toro ricavata con il metodo generale delle superfici di rotazione

Ricaviamo ora l'equazione del toro, seguendo il metodo generale illustrato inizialmente QUI:

a) determiniamo una qualsiasi terna di parametri direttori dell'asse di rotazione. Anche stavolta, trattandosi dell'asse z, la terna di parametri direttori più semplice è (0,0,1);

b) consideriamo un qualsiasi punto appartenente alla curva che ruota intorno all'asse. Nel caso in argomento, la curva che ruota è una circonferenza di raggio r  , giacente, per semplicità nel piano coordinato xz e il cui centro C giace, per semplicità, sull'asse x a distanza R dall'asse z. Il centro di tale circonferenza ha, dunque coordinate (R, 0,0).  Una tale circonferenza sarà individuata dal sistema di equazioni:

La prima equazione questa esprime la condizione che deve essere soddisfatta da tutti i punti della circonferenza, ossia che la loro distanza dal centro è costante e pari al raggio r. La seconda equazione esprime la condizione che la circonferenza giace sul piano xz, quindi tutti i suoi punti hanno la coordinata y nulla.

Considerato che , nel nostro caso,  e , svolgendo i calcoli si ha:

Dalla prima mi ricavo z:

Un qualsiasi punto P di tale circonferenza avrà, dunque, coordinate 

Troviamo ora l'equazione del piano passante per P e perpendicolare all'asse di rotazione (utilizzando i parametri direttori trovati in a):

cioé:

              (1)

c) consideriamo un punto  qualsiasi dell'asse di rotazione e determiniamo l'equazione della sfera avente centro in  e raggio pari a  . Naturalmente, poiché anche stavolta l'asse passa per l'origine degli assi, per rendere semplici i conti, prendiamo come punto  proprio l'origine degli assi O (0,0,0). La sfera cercata, quindi, avrà equazione:

               (2)

cioè, ricordando le coordinate del punto generico P della circonferenza generatrice:

cioè:

                    (3)

Dalla (2), inoltre, messa a sistema con la (1), si ha:

da cui

     (4)

(ho preso solo il risultato positivo poiché il centro della circonferenza giace sul semiasse positivo della x ed r si considera <=R, quindi tutta la circonferenza generatrice giace nel semipiano positivo xz)

Sostituendo ora la (4) nella (3) , si ottiene:

            (5)

Questa è, dunque, l'equazione del toro oggetto di studio. Notiamo che quando R attinge il valore 0,  la (5) si trasforma nella:

che è proprio l'equazione della sfera con centro nell'origine e raggio r, in accordo con l'animazione grafica vista all'inizio dell'articolo.

 

Alcune sezioni particolari del toro

Ora divertiamoci a sezionare il toro in diversi modi. Consideriamo come piano secante il piano coordinato xy, di equazione z=0. Per determinare l'equazione cartesiana dell'intersezione tra toro e piano xy basta mettere a sistema le due equazioni (5) e z=0, ottenendo:

         (6)

Introduco una variabile ausiliaria

              (7)

Pertanto, la (6) diventa:

che è una normalissima equazione di secondo grado di cui sappiamo ricavare le soluzioni. A conti fatti, avremo:

quindi, per la (7):

cioè:

e queste sono le equazioni delle due circonferenze con centro nell'origine degli assi, giacenti sul piano coordinato xy e aventi raggio, rispettivamente R+r  e R-r , visibili in blu nella seguente figura.

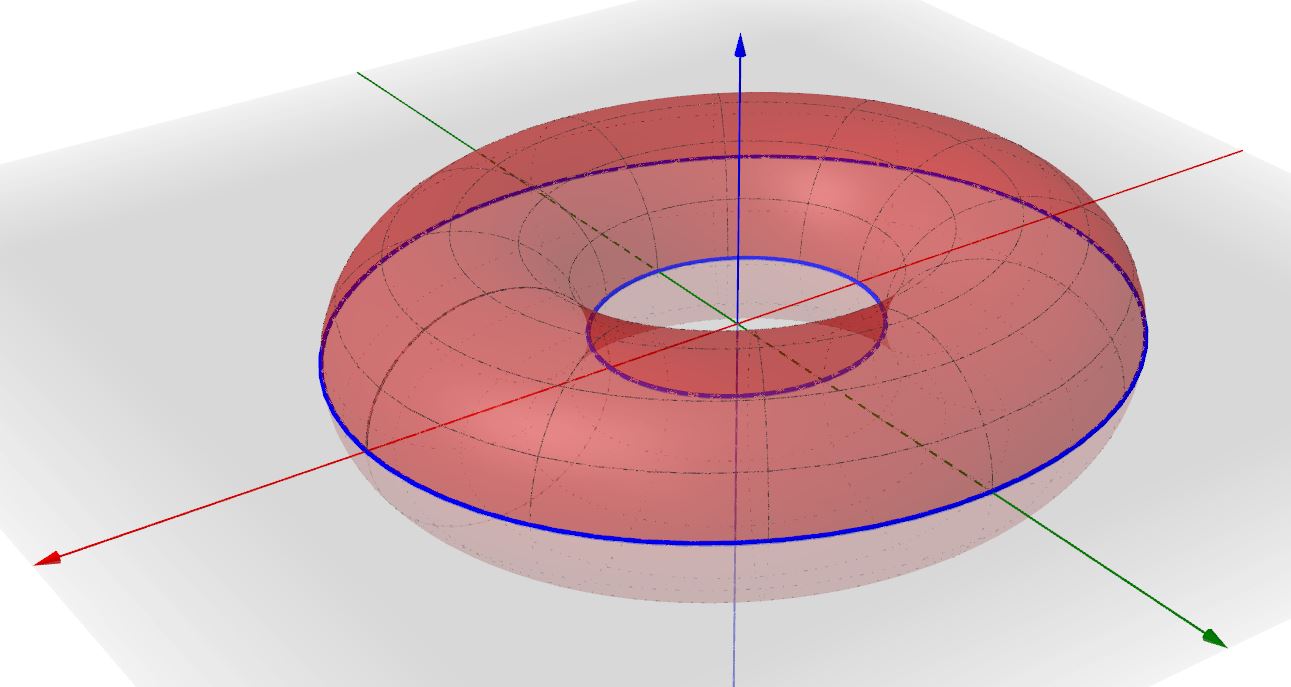
E se sezioniamo il toro con il piano coordinato yz , di equazione x=0 ? Semplice, basta metere a sistema l'equazione del toro (5)  con l'equazione del piano secante x=0. La (5) , stavolta, si trasforma così:

che posso scrivere come:

cioè:

e queste sono le equazione delle due circonferenze giacenti sul piano coordinato yz, di raggio r e aventi il centro distanziato di R e -R rispettivamente,  dall'origine, circonferenze visibili in verde nella seguente figura.

 

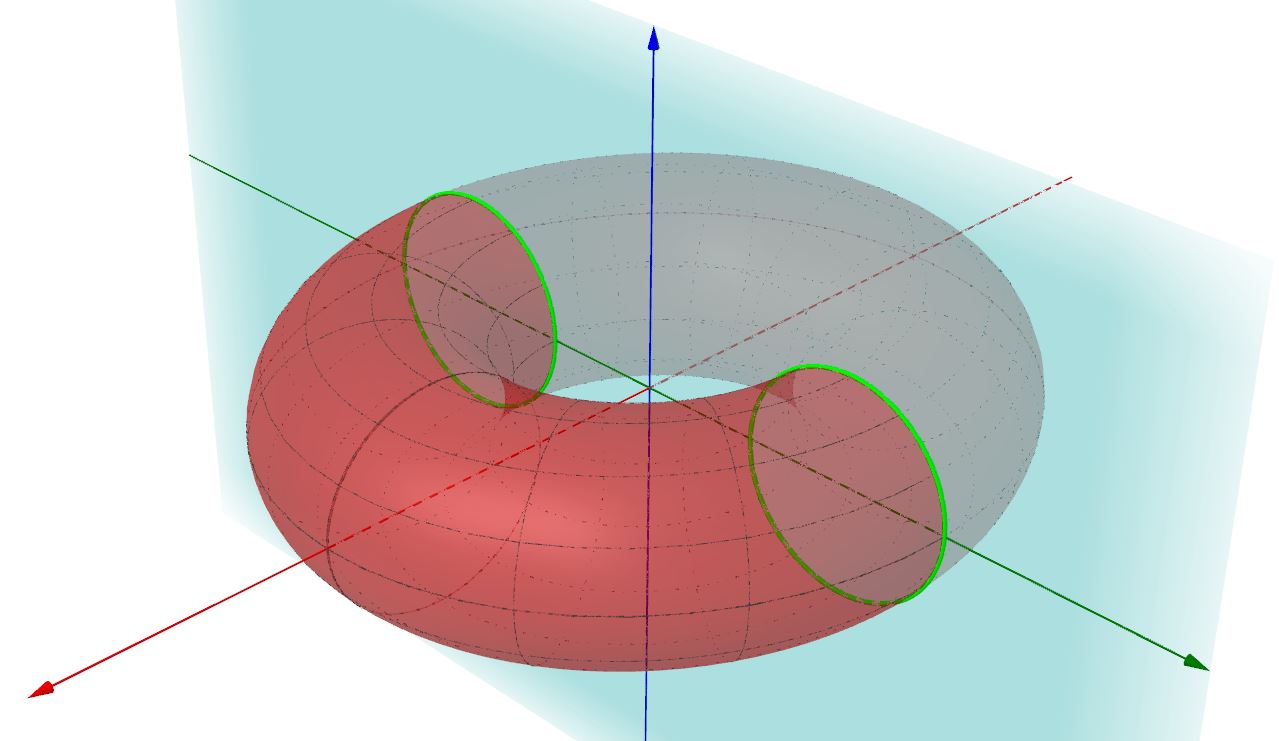
Stesso ragionamento se sezionassimo il toro con il piano coordinato xz, di equazione y=0.

 

Equazione cartesiana del toro ricavata per altra via

Nel caso del toro, si può giungere a ricavare la sua equazione cartesiana (5) anche per altra via, oltre che mediante il metodo visto sopra, assolutamente generale e valido per qualsiasi superficie di rotazione.

Facciamo riferimento alla seguente figura.

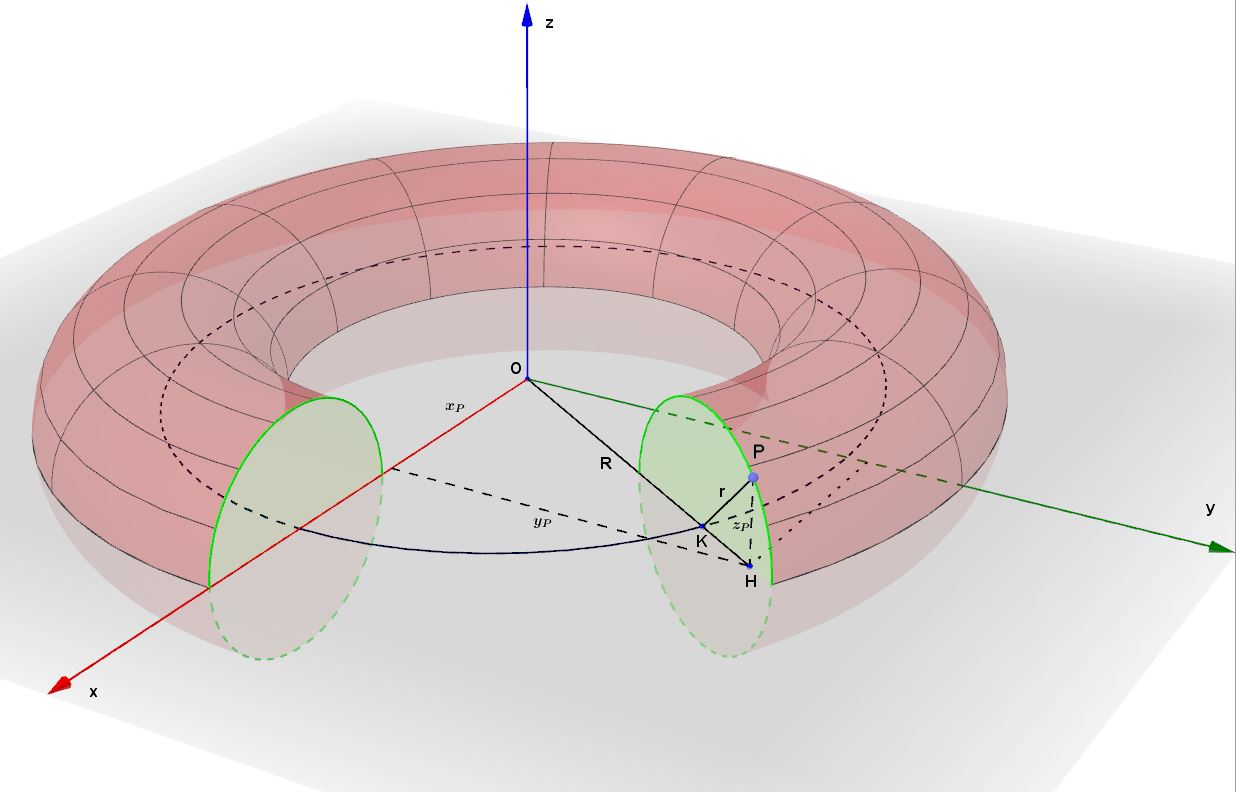
Si ragiona esclusivamente sulle caratteristiche geometriche del toro. La sua peculiarità è che ogni suo punto P giace su una circonferenza contenuta in un piano verticale passante per l'asse z, di raggio r e che ha il centro a sua volta giacente su una circonferenza contenuta nel piano xy , di raggio R e centro nell'origine degli assi. Consideriamo, allora, il triangolo rettangolo PHK e applichiamo ad esso il teorema di Pitagora:

               (8)

PK lo conosciamo ed è pari ad r. OH lo conosciamo ed è pari alla coordinata  del punto P. Non conosciamo ancora KH. Ma esso si ricava per differenza tra il segmento OH e il segmento OK. Per trovare l'espressione di OH, consideriamo uno dei due triangoli rettangoli aventi ipotenusa coincidente con OH. Applicando anche stavolta il teorema di Pitagora e constatando che i due cateti non sono altro che la coordinata x e la coordinata y del punto P, avremo:

OK, invece, è semplicemente il raggio R della circonferenza principale del toro. Quindi

Dunque, la (8) diventa:

Poiché questa relazione vale per qualsiasi punto P, generalizziamo le sue coordinate indicandole semplicemente con x, y, z. Svolgiamo il quadrato a secondo membro e ordiniamo, ottenendo alla fine:

ossia proprio l'equazione (5) già ricavata con il metodo generale.

 

Equazione parametrica del toro 

E' interessante determinare anche l'equazione parametrica del toro, ossia non in funzione delle coordinate cartesiane x,y,z di un suo punto, ma in funzione di due parametri geometrici che caratterizzano ciascun suo punto.

Facciamo riferimento alla seguente figura:

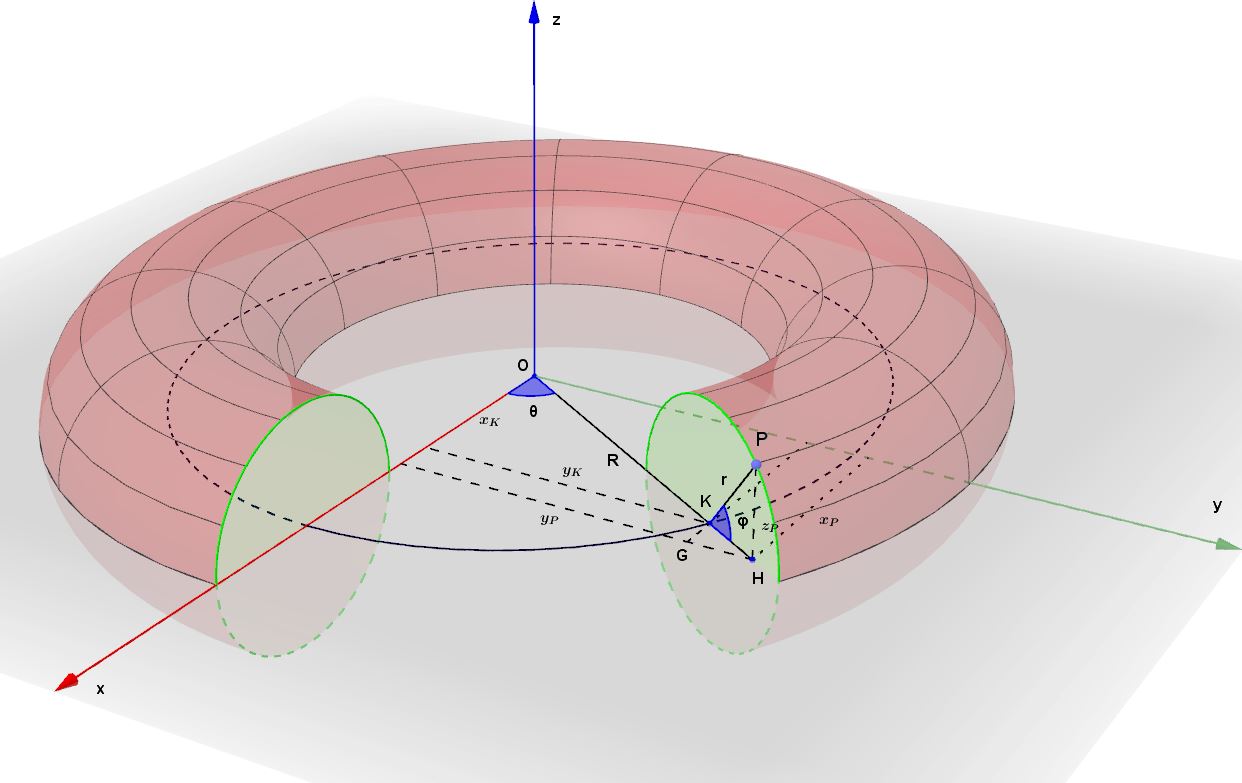
In essa ho evidenziato i due parametri caratteristici di ciascun punto situato su una superficie toroidale: l'angolo  e l'angolo . Per generare un toro, essi variano entrambi tra 0 e 360°. Esprimo, ora, le coordinate cartesiane del centro K della circonferenza generatrice passante per il generico punto P del toro in funzione di detti due parametri. Considero uno dei due triangoli rettangoli aventi ipotenusa OK ed applico i teoremi trigonometrici sui triangoli rettangoli:

Ora esprimo le coordinate cartesiane del punto P del toro in funzione dei parametri suddetti, constatando che il triangolo KGH è anch'esso rettangolo:

Essendo le suddette equazioni valide per ogni punto P del toro, generalizziamo indicando le sue coordinate con x,y,z. Otteniamo quindi:

Queste sono le equazioni parametriche del toro. Esse , tra l'altro, consentono di rappresentare graficamente, per esempio utilizzando software come Geogebra, non solo un toro completo, ma anche porzioni di toro, semplicemente limitando l'intervallo di variazione dei due parametri  e  . La figura seguente illustra, per esempio, un tronco di toro ottenuto limitando il parametro  tra 60° e 225° :

Area e volume del toro e ..affinità con il cilindro

Nonostante il toro abbia un'equazione cartesiana non semplicissima, è, invece, molto facile calcolare la sua area, anche senza fare uso di integrali doppi. Basta osservare  la sua conformazione. In pratica, come abbiamo visto, esso si ottiene facendo ruotare una circonferenza attorno ad un asse. E' intuitivo, quindi, pensare che l'area della sua superficie si ottiene semplicemente come nel caso del cilindro (delimitato in altezza). Nel caso del cilindro si moltiplica la lunghezza della circonferenza di base per la sua altezza. Nel caso del toro, la circonferenza è quella generatrice e l'altezza è rappresentata dalla lunghezza della circonferenza principale di raggio R. Avremo quindi:

cioè:

Analogamente, considerando il solido racchiuso dalla superficie toroidale, il suo volume si calcola semplicemente come nel caso del cilindro (area del cerchio di base moltiplicata per l'altezza). Nel nostro caso, moltiplicheremo l'area del cerchio delimitato dalla circonferenza generatrice per la lunghezza della circonferenza principale, di raggio R:

cioè:

Quella tra il toro (di raggio principale R) e il cilindro (di altezza 2R) è una affinità (passatemi il termine) interessante. Il toro, infatti, possiamo pensarlo come un cilindro ripiegato in maniera tale da far coincidere le sue due basi. Al contrario, potremmo pensare la superficie cilindrica di raggio r come un toro di raggio principale R infinito. L'affinità tra le due superfici emerge anche analiticamente considerando le rispettive equazioni cartesiane. Quella del toro è la (5) trovata nei precedenti paragrafi:

                   (5)

Il cilindro di cui dobbiamo considerare l'equazione è quello di raggio r e con asse parallelo al piano xy e distante R dal piano yz. Facciamo riferimento alla seguente figura:

Per tutti i punti di tale cilindro vale la condizione che la distanza dall'asse del cilindro è costante e pari ad r. Quindi:

cioè:

                (9)

Guardando le suddette due equazioni, la (9) e la (5) , notiamo che si somigliano parecchio. Basta infatti porre nella (5):

per avere:

E quest'ultima è proprio formalmente identica alla (9), con la differenza che al posto della variabile  x c'è la variabile t.

Per concludere, ai seguenti link potete visualizzare direttamente il toro sull'applicazione online Geogebra , potendolo così manipolare come preferite.

Versione classica: https://ggbm.at/yymdkgvu

Versione 3D visualizzabile con occhiali anaglifici: https://ggbm.at/khm5gnqw

Appena definita, verrà pubblicata una appendice a questo articolo, in cui verrà approfondito l'argomento delle sezioni del toro con un piano (le "toriche", per analogia a quelle del cono che sono note come "coniche"). Il toro: una superficie di rotazione che non finisce mai di sorprendere...

---

Quelli che seguono sono i links a tutti gli articoli di geometria solida sinora pubblicati, prima di questo:

1. Introduzione alla geometria dello spazio (prima parte)
2. Introduzione alla geometria dello spazio (seconda parte)
3. Introduzione alla geometria dello spazio (appendice)
4. Geometria dello spazio (terza parte)
5. Geometria dello spazio (quarta parte)
6. Geometria dello spazio (quinta parte)
7. Geometria dello spazio (sesta parte)
8. Geometria dello spazio (settima parte - altri esempi di superfici di rotazione )

Li trovate anche nell'ARCHIVIO