Cominceremo come per un solito quiz, ma poi seguirà un aiutino e infine la risposta. Ognuno si fermi dove preferisce e provi a dare una risposta nei commenti... Aggiungiamo che questo esercizio è alla portata delle scuole medie inferiori, come dimostra l'unico asterisco assegnatogli.

Siamo su una delle piazze più grandi del mondo, perfettamente orizzontale e liscia. La piazza, però, è soprattutto molto lunga e molto meno larga. Al suo centro è stata innalzata una torre fantastica che i governanti della nazione dicono sia la più alta del mondo. In realtà, sembra davvero molto alta, ma io non creo alle misure riportate dalla stampa locale e vorrei misurarne direttamente l'altezza. Forse, per paura che qualcuno abbia la mia stessa idea, è stato vietato l'accesso alla torre e si deve stare a una distanza ragguardevole da lei. Per terra è chiaramente segnalato il divieto di oltrepassare una certa linea che gira attorno alla costruzione (LI). E' meglio non tentare di fare i furbi, dato che la polizia locale non usa maniere molto gentili...

L'unica cosa certa è che la distanza della linea dalla torre è poco più corta dell'altezza dell'enorme costruzione. La piazza dicono, invece, sia larga poco più di due volte l'altezza della Torre. Sono dicerie, ipotesi, che ben poco servono per avere misure precise. Tutto è da confermare sul campo. Sicuramente,  non posso assolutamente misurare  direttamente la distanza tra me (G) e la torre T!

Fortunatamente posso muovermi dove voglio nel resto della piazza  e ho con me un goniometro G che funziona  sia per misurare angoli  in verticale che in orizzontale. La situazione, vista dall'alto, è quella  mostrata nella Fig. 1 (dove a destra è anche rappresentato lo schema del goniometro).

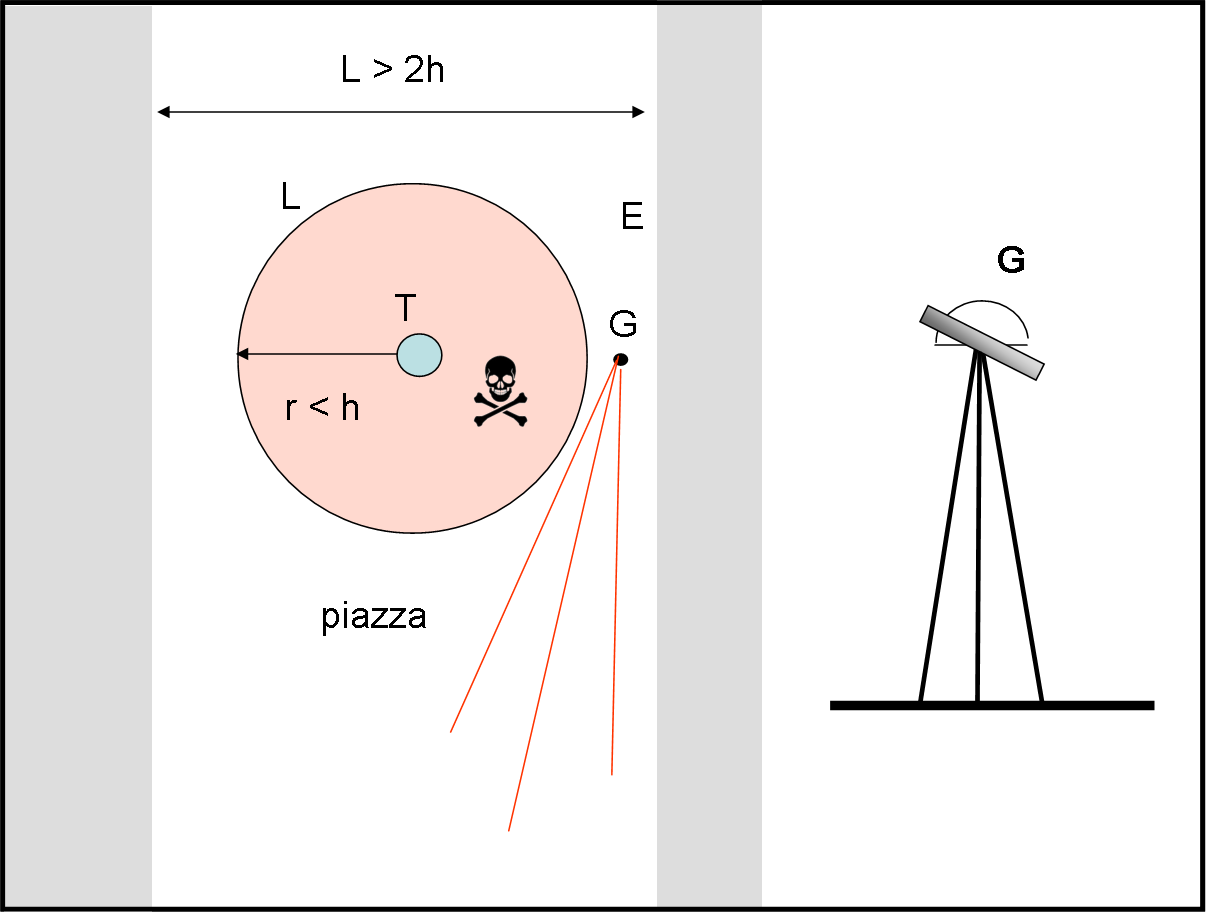
Fermo restando che posso sempre misurare delle distanze nella piazza con il mio metro arrotolabile molto lungo (basta che non tocchi il limite invalicabile), ci penso un po' sopra e poi, con due sole misure fatte col goniometro in posizione verticale e una in posizione orizzontale, risolvo il problema.

Avevo proprio ragione... la torre è alta, ma non la più alta.

Come ho fatto a calcolarne l'altezza in modo abbastanza preciso? Tocca a voi rispondere... La faccenda si risolve in modo veramente elementare senza scomodare la trigonometria. Bastano le nozioni di geometria delle scuole medie. Consideriamo anche nulla l'altezza del goniometro dal suolo.

 

Aiutino piccino piccino

Un piccolo aiuto per chi ha provato, ma è un po' in crisi...  Ricordate Pitagora... basta e avanza!

Se Pitagora non vi ha aiutato, continuate a leggere.

 

*****************************************************************

 

Soluzione

La prima cosa da fare è riuscire a riportare sul terreno l'altezza della Torre, anche se non può essere misurata direttamente. Dato che la posizione di G si trova tra una distanza minore dell'altezza della Torre (r) e una distanza maggiore (L/2), non è difficile muovere in senso orizzontale G (facendo riferimento alla figura), nel poco spazio a disposizione, fino a misurare esattamente un angolo di 45°. Quello sarà il punto esatto in cui la distanza tra me e la Torre è esattamente uguale all'altezza della Torre. Siamo, infatti, di fronte a un triangolo rettangolo isoscele (ABG), in cui i due cateti risultano uguali (Fig. 2). Sono sicuro di raggiungere quella posizione perché l'altezza della torre sul terreno (BG) deve essere compresa tra BL e BE.

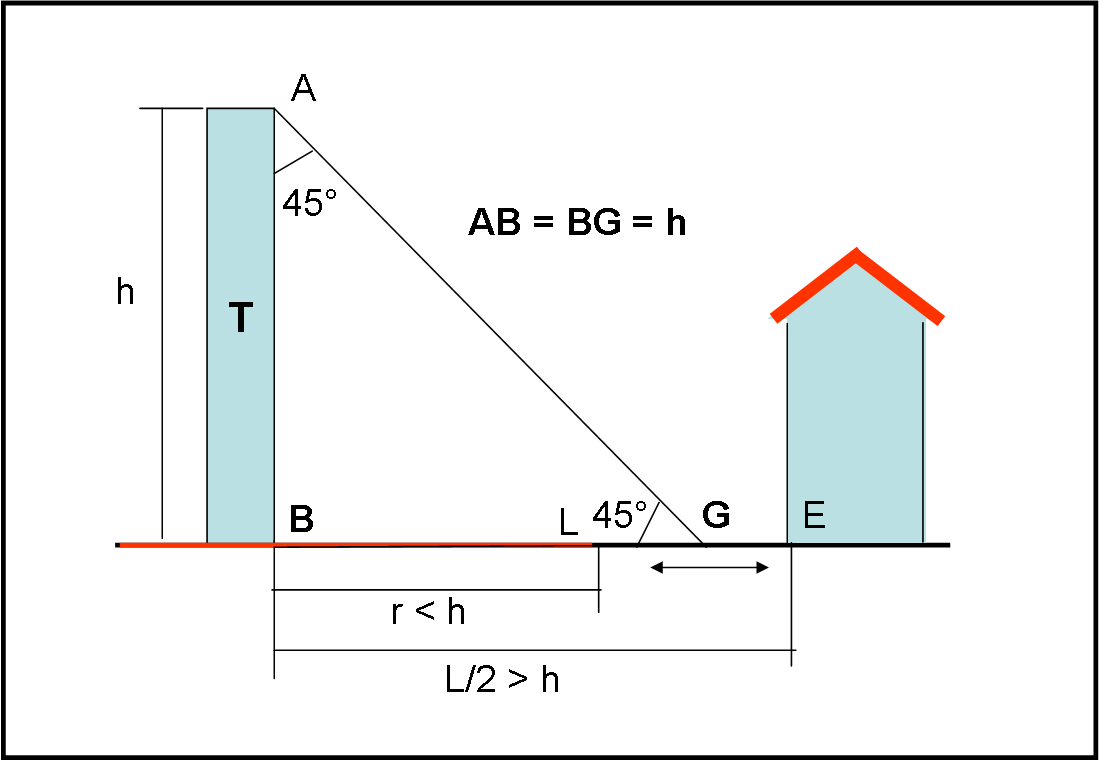
Avrei già raggiunto il mio scopo, ma, purtroppo non posso assolutamente misurare GB, dato che LB è terreno inviolabile! Poco male, si può superare questo ostacolo... Segno per bene la posizione G  sul terreno e  mi muovo  verso il basso di Fig. 1, perpendicolarmente alla direzione BG, per un tratto piuttosto lungo e segno questa linea per terra (meno male che non si preoccupa nessuno se sporco un poco il terreno...). Questa operazione  riesco a farla molto bene con il goniometro usato orizzontalmente (ve lo dice un ex ufficiale topografo!). Mi sposto in G', G", G''' lungo questa linea (Fig. 3), sapendo molto bene che ogni triangolo BGG', BGG", BGG''' è rettangolo in G.

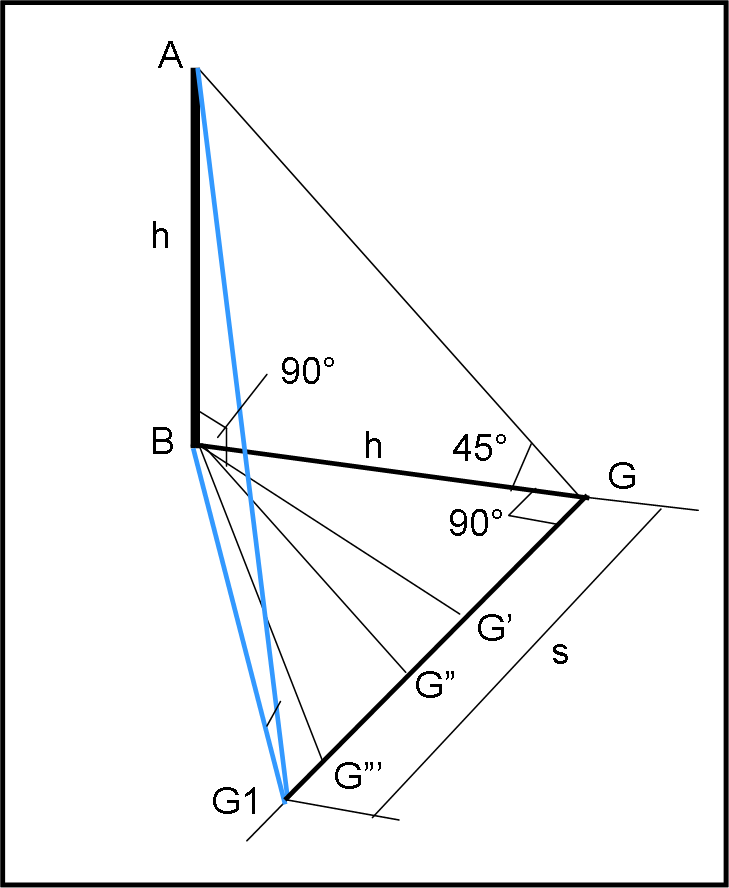
In parole matematiche (teorema di Pitagora):

BG'² = BG² + GG'²

BG''² = BG² + GG"²

BG'''² = BG² +  GG'''²

......

Ricordiamo che BG = h e che GG' o GG" o GG''' sono lunghezze s misurabili lungo la linea tracciata per terra.

Ogni tanto mi fermo e con il goniometro usato verticalmente misuro l'angolo AG'B. E' anche ovvio che il triangolo AG'B è rettangolo in B. Quando mi fermerò definitivamente? Beh... è molto semplice: quando l'angolo AG1B diventa esattamente di 30°!

Calcolo subito l'ipotenusa del triangolo BGG1, che per quanto detto poco fa, vale:

BG1² = BG² + GG1²

ma BG è proprio h mentre GG1 è uguale a s e lo posso misurare tranquillamente.

BG1² = h² + s²              .... (1)

Poniamoci adesso nel piano del triangolo ABG1 e disegniamo la Fig. 4.

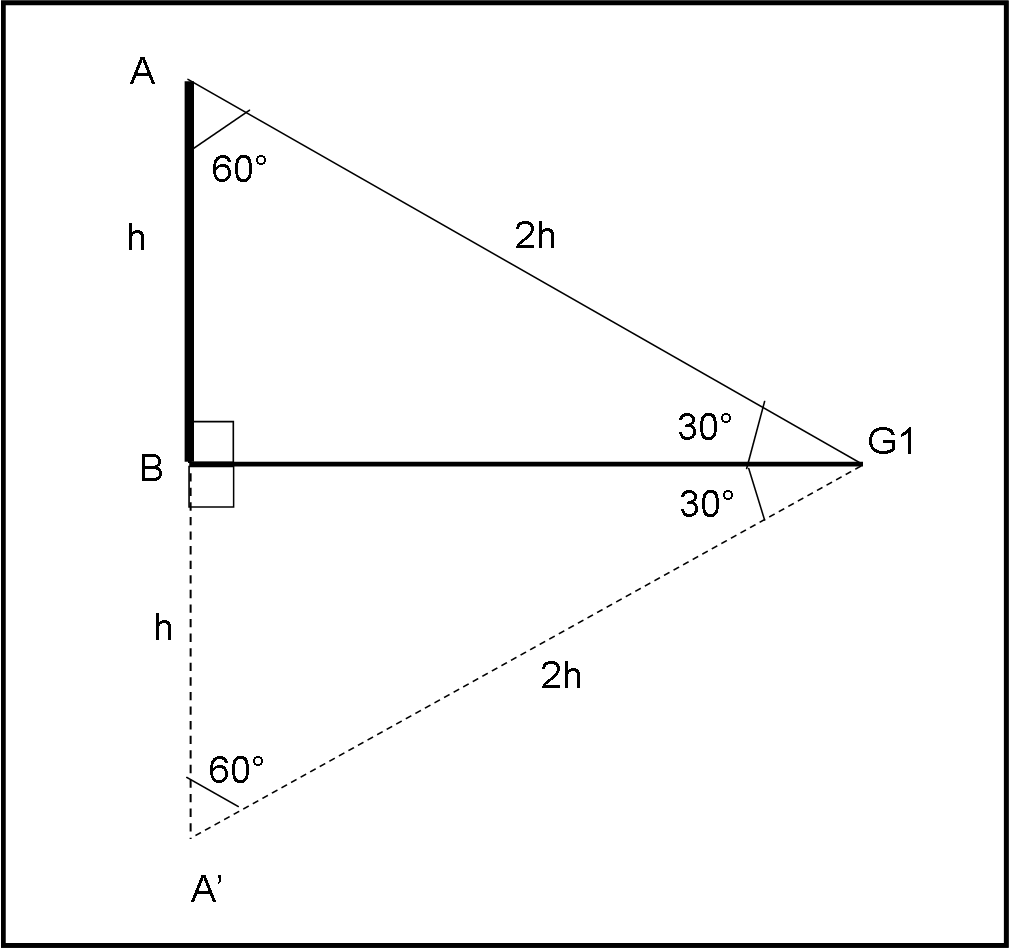
Dato che l'angolo AG1B è di 30°, l'angolo BAG1 deve essere di 60°. Ma, allora, se ribaltassi il triangolo ABG intorno a BG, otterrei un triangolo AA'G1 che è equilatero. Se è equilatero vuole anche dire che i tre lati sono uguali, ossia AA' = AG1 = G1A'. Ma AA'  è proprio uguale a 2h.

Non mi resta che calcolare BG1 dal triangolo BAG1, applicando nuovamente il teorema di Pitagora:

BG1² = AG1² - AB1²

BG1² = (2h)² - h² = 4h² - h² = 3h²

A questo punto, basta ricordarsi della (1) e scrivere:

h² + s² = 3h²

da cui:

2h² = s²

h² = s²/2

h = s/√2                       .... (2)

Il problema è risolto... tuttavia, si possono fare altre considerazioni di estrema semplicità...

 

Considerazioni varie

Se non ci fosse stato il palazzo E, ossia se la piazza fosse stata più larga, sarebbe bastato indietreggiare fino a che l'angolo AGB fosse stato di 30°. Non avrei dovuto usare il goniometro in senso orizzontale. Infatti, la Fig. 5 lo mostra molto bene...

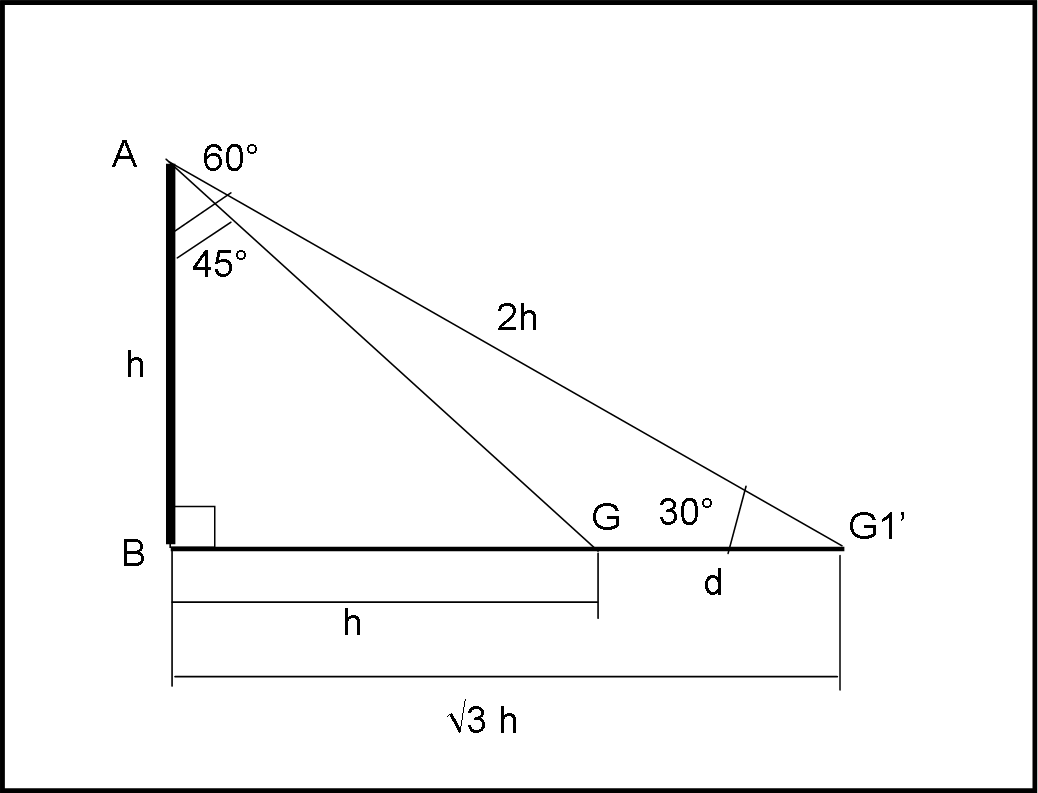
GG1' sarebbe stata l'unica lunghezza misurabile e avrei scritto, ricordando che BG1 = √3 h

(BG1'² = 4h² - h² = 3h²)

GG1' = d =√3 h - h = h (√3 - 1)

da cui:

h = d/(√3 - 1)               .... (3)

Non stupiamoci se il risultato sembra diverso dal caso trattato precedentemente: d e s sono due lunghezze diverse, ma il risultato è lo stesso. Lo vediamo in Fig. 6 che riprende le due configurazioni dall'alto.

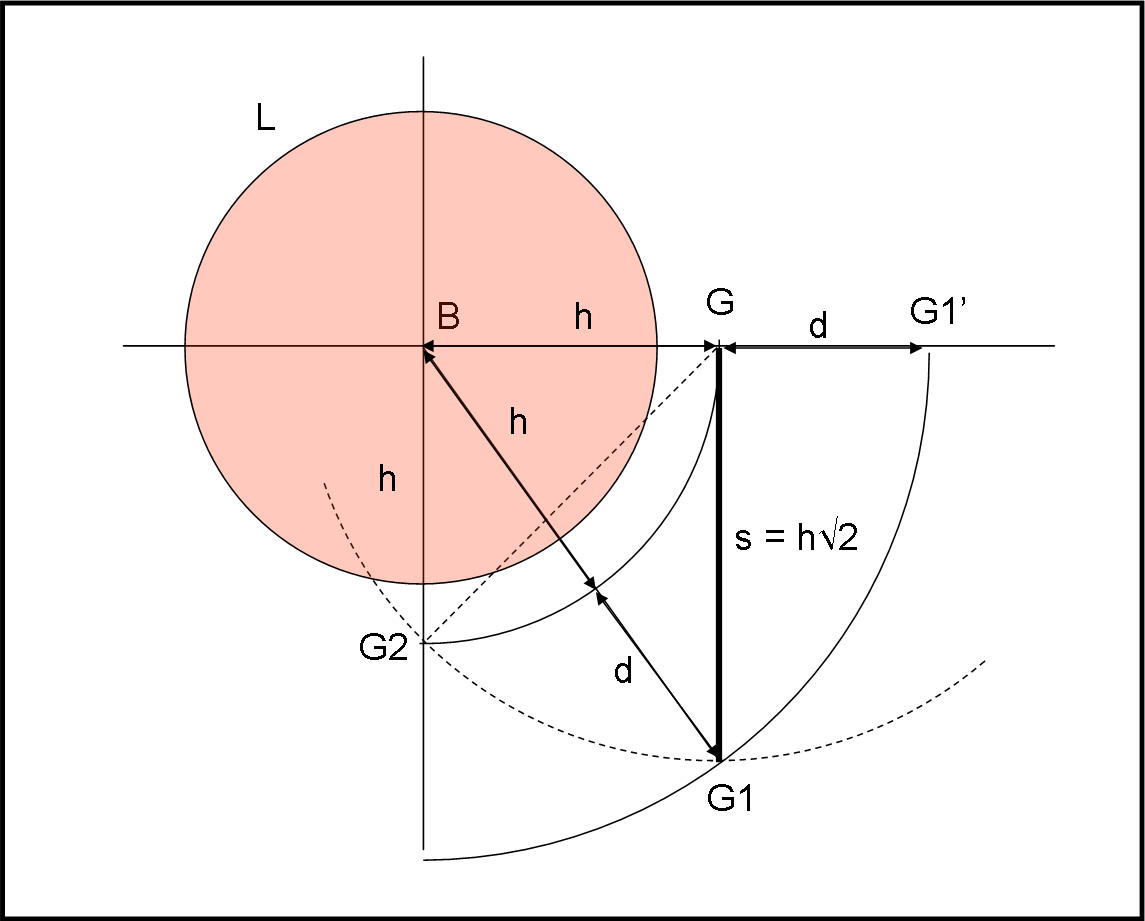
Possiamo formalmente passare da una soluzione all'altra, lavorando sul triangolo rettangolo BGG1

BG1 = h + d

GG1 = s

BG1² = GG1² + BG²

(h + d)² = s² + h²

s² = (h + d)² - h²

Ma sappiamo dalla (2) che:

s² = 2h²

per cui si può scrivere:

2h² = (h + d)² - h²

(h + d)² = 3h²

h + d = √3 h

h = d/(√3 -1)

che è proprio la (3).

Possiamo fare ancor un paio di ulteriori considerazioni, sempre basandoci sulla Fig. 6.

Se la zona limite fosse leggermente più ristretta si potrebbe tranquillamente andare da G a G2. G2 vedrebbe nuovamente la torre sotto un angolo di 45° e quindi il percorso GG2 sarebbe uguale all'altezza h moltiplicata per √2. In altre parole, GG2 sarebbe la diagonale del quadrato di lato h.

Ma anche il risultato datoci dalla (1) ci dice che il segmento GG1 = s deve essere la diagonale di un quadrato di lato h, dato che vale proprio s = h √2. Basta poco per visualizzare questo risultato... Basta tracciare la circonferenza di centro G e raggio GG2 per vedere che GG1 è uguale a GG2, essendo entrambi raggi di una circonferenza di raggio h√2.

Ci siamo accorti che partendo da un esercizio di livello di difficoltà  veramente basso (ci vuole solo un minimo di riflessione)  ci si può divertire cercando soluzioni e conseguenze di carattere più peculiare o generale di indubbio interesse. La geometria e il suo linguaggio, pur se a livello molto semplice, ci sono di grande aiuto nella risoluzione di problemi estremamente pratici.

 

Se vi è piaciuto questo NON-QUIZ, ne trovate altri QUI