Categorie: Fisica classica
Tags: accelerazione derivate derivate successive jerk moto velocità
Scritto da: Maurizio Bernardi
Commenti:7
Jerk, Snap, Crunkle & Pop: cinquanta sfumature di moto **
Questo articolo è stato inserito nella pagina d'archivio "Dinamica e meccanica", compresa in "Fisica classica"
Non bastava l'accelerazione a complicare la vita! Adesso arriva anche il jerk e si tira dietro tutti i suoi parenti.
E va bene, via, riprendiamo il discorso e vediamo che altro ci aspetta!
“Sono veramente desolata, ma temo che anche quest'anno dovremo bocciarlo...”
La preside dell'unico liceo scientifico di Elea fissò a lungo la donna seduta davanti alla sua scrivania, in evidente imbarazzo.
“Noi, a casa, abbiamo fatto di tutto... è un ragazzo testardo, anche se a suo modo è intelligente...”
“Lo sappiamo, lo sappiamo... ma capisce, è anche un elemento di disturbo per il resto della classe, proprio per il fatto che, con quel suo modo di ragionare, disorienta gli alunni e anche qualche insegnante.”
“Pensi, signora preside, che questa estate, invece di fare i compiti delle vacanze, ha passato tutto il tempo in giardino camminando dietro alla sua tartaruga.”
“Capisco, l'insegnante di matematica mi ha raccontato qualcosa. Ma anche l'insegnante di educazione fisica si è lamentato, sa? Dice che si rifiuta di correre, con il pretesto che, per arrivare al traguardo, dovrebbe prima arrivare a metà strada e, una volta lì, dovrebbe arrivare a metà del percorso rimanente, e poi ancora a metà e così via, insomma, dato che, sostiene lui, il traguardo non lo potrebbe mai raggiungere, è inutile mettersi a correre.”
La signora Zenone si asciugò una lacrima che le era spuntata nell'angolo esterno dell'occhio destro. Prese guanti e borsetta e si alzò tendendo la mano alla preside.
“Signora Zenone, da mamma a mamma, è meglio se ne parla ad uno psichiatra, sa?”
Nell'atrio di Casa Zenone il pavimento era cosparso di minute schegge di vetro. Una freccia giaceva in mezzo a quei frammenti luccicanti, fornendo una plausibile spiegazione alla loro origine.
“Che disastro ! Adesso quando torna tuo padre, Teleutagoras, te la vedrai con lui! Ma come si fa a giocare con arco e frecce in casa? Dove hai la testa?”
“Mamma, non so cosa sia successo, ma ti assicuro che non può essere colpa mia...”
“Certo, vuoi dire che la colpa è della freccia, vero?”
“No, no ! La freccia non può essere stata, poverina. La freccia, si sa, non si può muovere, se vuoi te lo posso spiegare.”
“Ma fammi il piacere, la freccia non si può muovere...”
La signora Zenone, si stava già dando da fare a raccogliere i vetri da terra. Si fermò solo un istante, per asciugare una lacrima che le stava spuntando nell'angolo esterno dell'occhio sinistro.
Se invece di ricorrere ad uno psichiatra, come suggerito dalla preside, la signora Zenone avesse portato, anche solo una volta, il figlio ad un Luna Park, e l'avesse piazzato su un ottovolante, il ragazzo avrebbe forse rivisto qualcuna delle sue idee sul moto.
Ma l'esperienza dell'ottovolante ha qualche cosa da insegnare anche a tutti coloro che hanno in mente il moto come qualcosa che nasce da una forza, che a sua volta risale ad una accelerazione, intesa come la derivata seconda dello spostamento, e pensano così di avere chiuso il discorso.
I fisici sono persone ossessionate dall'idea dei rapporti, intendo i rapporti tra quantità variabili nel tempo. La percentuale di decadimento dei nuclei radioattivi, per esempio, o l'evolversi delle quantità di elementi nel corso di una reazione chimica, o il rapporto tra lo spazio percorso e il tempo impiegato, insomma, una mania apparentemente innocua.
Si comincia parlando di spazio e di spostamento in un intervallo di tempo. Ecco quindi la velocità, nient'altro che la derivata prima della dislocazione rispetto al tempo.
v = dx/dt
cosa ci può mai essere di più intuitivo?
Ma, per un oggetto che inizia a muoversi, un oggetto che, prima, era proprio “fermo”, come si passa da velocità zero a velocità uguale a qualcosa?
Semplice, grazie alla variazione della velocità, che in un certo intervallo di tempo passa da zero ad un valore finale. Ecco, la variazione della variazione della posizione nel tempo: la accelerazione.
a = dv/dt = d2x/dt2 la derivata seconda…
Sì, la derivata seconda, l'accelerazione! Quella di F=ma, appunto lei.
Però... se l'oggetto parte da fermo, la sua accelerazione iniziale era zero. Vuol dire che ad un certo punto è cresciuta fino a raggiungere un certo valore. Insomma, esiste una variazione della accelerazione. A pensarci bene esiste una variazione anche quando siamo già in movimento accelerato, se acceleriamo ancora un po' o, viceversa, se freniamo.
E cosa sarà mai questa variazione di accelerazione? Ma la derivata terza dello spazio, rispetto al tempo, ovviamente!
Questa cosa si chiama Jerk, che tradotto in italiano suonerebbe “strappo”
j = da/dt = d2v/dt2 = d3x/dt3
Le prime due derivate dello spazio sono concetti del tutto intuitivi, tangibili, ben presenti a tutti nella esperienza quotidiana, e di cui si parla molto a scuola.
Ciò che non viene normalmente rivelato agli studenti, è il fatto che, nel definire la seconda legge della dinamica, Newton usò queste precise parole:
“Lex II: Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur.”
“Un cambiamento nel moto è proporzionale alla forza motrice impressa e si manifesta in linea retta nella direzione di tale forza.”
Qeste parole fanno intendere che una forza impulsiva, che agisse in un certo intervallo di tempo Δt, produrrebbe una accelerazione che non può essere costante (se la massa del corpo non varia).
Il jerk, pur essendo inevitabilmente presente ogni volta che variamo l'accelerazione, è più elusivo, non se ne parla.
Eppure il concetto di derivata terza, magari non esplicitamente, è presente anche in discorsi che si sentono comunemente in TV. Per esempio un presidente degli USA (Nixon), parlando della inflazione, ebbe a dire: “Il tasso di incremento della inflazione sta diminuendo”, usando il concetto di derivata terza. Infatti il tasso di inflazione è il ritmo di crescita nel tempo, ossia la derivata prima, dei prezzi. Il tasso di crescita della inflazione non è altro che la derivata seconda, e se diciamo che sta calando, allora stiamo parlando della derivata terza. Nel caso citato da Nixon i prezzi erano in salita e la velocità della salita era crescente, ma il ritmo di questa "crescita della velocità" stava rallentando.
Ora che ci avrete preso gusto, vorrete sapere delle altre derivate...
Ebbene, la derivata quarta si chiama Snap. La traduzione di snap è semplicemente “schiocco” , come il rumore della frusta, o quello che si fa con le dita. Alcuni preferiscono usare il termine Jounce che significa “sballottamento”, nel senso di scuotimento.
La derivata quinta si chiama Crackle e la sua traduzione è “crepitio”
La derivata sesta si chiama Pop e la probabile traduzione è “scoppio”.
Fermiamoci qui, per favore, anche perché ai fini pratici la nostra capacità di valutazione si ferma alla derivata quarta.
A parte la forza di gravità che ben conosciamo, il concetto di forza costante è piuttosto raro nella vita quotidiana. L'accelerazione che imprimiamo alla nostra auto quando il semaforo passa dal rosso al verde, non è costante. La sua crescita produce una sensazione “jerk” ed eventualmente “snap” , se il jerk non si mantiene costante.
Ancora più evidente è quello che si prova su un ottovolante o lanciandosi da un trampolino.
La maggior parte dei mezzi di trasporto, ascensori, treni, navi, aerei, sono progettati e manovrati in modo da minimizzare gli effetti biomeccanici sul passeggero. Ciò non vale per gli ottovolanti che sono volutamente studiati per stimolare i sistemi sensoriali, visivi, auditivi e vestibolari. I soggetti che usufruiscono di queste strutture ludiche sono deliberatamente esposti ad accelerazioni elevate la cui intensità, durata e variabilità sono sotto controllo. Queste variabili vengono spinte per esaltare gli stimoli sensoriali, ma anche regolate per restare entro i limiti di sicurezza. Gli effetti conseguenti alla esposizione ad accelerazioni elevate e rapidamente variabili, possono risultare decisamente spiacevoli o addirittura nocivi per la salute. Per questo motivo la progettazione di queste strutture è soggetta a severi controlli.
Jerk e Snap sono osservabili in vasti settori della fisica e dell'ingegneria. Prima di tutto nei moti in cui compaiono vibrazioni, in particolare nei fenomeni di risonanza. Sono presenti nei transitori di apertura/chiusura come decollo e atterraggio e accelerazione/decelerazione.
Una accelerazione priva di Jerk non potrà mai causare vibrazioni. Ad esempio durante una operazione di tornitura le vibrazioni che possono manifestarsi, mettendo a rischio il risultato della lavorazione sono causate da Jerk e Snap. In tutti i processi produttivi dell'ingegneria meccanica, ad esempio riguardanti il settore automobilistico, è vitale tenere sotto controllo queste variabili per ottenere superfici esenti da irregolarità di lavorazione. Nella ingegneria civile, i tracciati dei binari ferroviari e delle strade devono tener conto in fase progettuale di precise regole nel raccordare tratti rettilinei e curvilinei, ricorrendo a curve di transizione che sono tratti di spirale di Eulero (Clotoide).
Lungo il percorso della Clotoide, la variazione di accelerazione non è discontinua e i livelli di Jerk, ed eventualmente di Snap sono ridotti in modo significativo. Viceversa, al variare improvviso dei raggi di curvatura, la sollecitazione del passeggero risulterebbe inaccettabile oltre a mettere il veicolo a rischio di uscita di strada.
L'obiettivo di un buon progettista è di ottenere come minimo un jerk graduale e uno snap costante, ossia un aumento graduale della accelerazione radiale, e ancor meglio, un jerk costante e uno snap nullo, ossia un aumento lineare della accelerazione radiale.
Anche nella progettazione degli ottovolanti, tracciando eliche e loops, si ricorre all'impiego di tratti a forma di clotoide per contenere gli effetti di jerk e snap.
Come avete certamente capito, il problema di fondo non è produrre il moto, ma controllarlo in tutte le sue bizzarrie, perché, anche se Zenone non ci credeva, la freccia si muove, eccome!
***********************************************************************
Piccola appendice per patentati
Al compimento dei diciotto anni, è quasi automatico iscriversi ad una scuola guida per prendere la patente. Un'ottima occasione per imparare un po' di dinamica “live”.
Purtroppo quasi mai questa opportunità viene colta. Al massimo ci si impadronisce inconsapevolmente di alcuni concetti, senza dar loro un nome preciso, una fisionomia.
Dare un nome agli oggetti e alle idee è una cosa fondamentale. Una idea senza un nome rischia di non esistere nella nostra testa.
Ora, la prima cosa che un diciottenne si sente dire è che non deve far spegnere il motore in partenza, lasciando andare bruscamente la frizione. Nessun istruttore di scuola guida vi dirà mai di abbassare il jerk. Pochissimi potrebbero invitarvi a fare in modo di non introdurre, nella dinamica del moto, derivate dello spazio rispetto al tempo superiori alla derivata seconda. Quasi tutti ricorrono, con toni più o meno gentili, alla frase stereotipata, peraltro di immediata comprensione: “Smettila di dare strappi con quella frizione, e stai attento a non spegnere il motore!” Certo, perché quando si spegne il motore, in un grafico della velocità in funzione del tempo, compare una bella linea verticale e questo significa che, senza la cintura di sicurezza, si andrebbe a sbattere la fronte contro il parabrezza.
La strumentazione di bordo non aiuta per nulla a capire questo semplice fenomeno. Abbiamo un contachilometri che registra lo spazio percorso, abbiamo un tachimetro, che segna la velocità istantanea, ma difficilmente vedremo sul cruscotto un accelerometro e, diciamoci la verità, anche se ci fosse...
Fatto sta che, strappo dopo strappo, in partenza e in marcia, il nostro patentando capisce come convincere la macchina a spostarsi docilmente da A a B. E' già qualcosa.
Con l'aiuto dell'istruttore (il cosiddetto ingegnere) è finalmente riuscito a evitare un sacco di jerk a sé e ai suoi trasportati, istruttore in primis. Ma lui non lo sa, anzi, possiamo dire “loro” non lo sanno, pur essendone contenti.
Ora è venuto il momento di affrontare una vera strada, un'autostrada. Naturalmente per entrare in autostrada ci sono le rampe di accesso, abbastanza lineari , come queste

O un po' più complicate, come queste

Vedete degli archi di cerchio in questa figura? Se li vedete vi sbagliate.
Immaginate come impostare la curva se, al termine di un rettilineo, notoriamente una funzione con raggio di curvatura infinito, vi trovaste davanti un tracciato che descrive un arco di cerchio, la cui curvatura è saldamente legata al raggio. Dovreste eseguire una brusca sterzata, tanto più brusca quanto più alta è la vostra velocità. Certo, andando lentamente... Ma le auto non sono nate per andare lentamente.
Cosa è mai quella sensazione che vi sale dallo stomaco, mentre la macchina vi fa capire che vorrebbe tanto ribaltarsi allegramente o scivolare fuori dalla carreggiata, per proseguire su quella riposante traiettoria rettilinea che stavate seguendo, invece di piegare verso il centro di rotazione?
State semplicemente provando cosa significa passare in modo non graduale da una accelerazione angolare nulla ad una accelerazione angolare finita. Non servono formule, è una cosa che si capisce subito, quando si prova, quando vi sembra di essere finiti in una scena di quei film d'azione in cui le macchine fanno mille capriole prima di fermarsi con le ruote all'aria.
La forza trasversale che sembra attrarvi verso l'esterno della curva, se solo aveste rallentato un po', sarebbe stata meno marcata, meno repentina. Meno “Jerk” e meno “Snap”.
Avete fatto un bel disastro, variando direzione e variando la velocità con cui avete cambiato direzione.
Meno male che in fondo al rettilineo qualche misconosciuto ingegnere ha pensato bene di non farvi trovare una curva circolare, ma un arco di spirale, un tracciato in cui il raggio di curvatura varia progressivamente, stringendosi o allargandosi a seconda delle necessità.
E qui arriviamo alla Clotoide. Eccola in tutta la sua misteriosa bellezza...
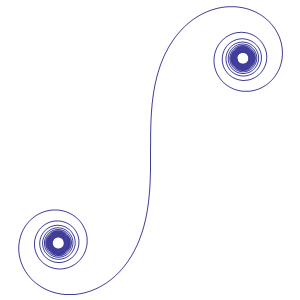
Beh, misteriosa perché non ne abbiamo scritto l'equazione. Se proprio avete questa curiosità... sappiate che esiste un modo per esprimere la curvatura K in funzione della ascissa curvilinea s (ossia la misura della distanza lungo il tracciato della curva).
Nel caso di una circonferenza, per esempio, questa rappresentazione è K= 1/r ( r è il raggio).
Per la clotoide invece K= s/a2.
Capite bene che la circonferenza ha una curvatura indipendente dalla ascissa curvilinea, sempre uguale. Viceversa la clotoide ha una curvatura che varia proporzionalmente al variare della ascissa curvilinea ( a è un parametro) è questo è molto utile per i progettisti delle linee ferroviarie , delle autostrade e, in ultima analisi, per voi.
Due parole sulla storia della clotoide ?
Si chiama anche spirale di Cornu o spirale di Eulero, ma il primo a studiarla deve essere stato Bernoulli, più di trecento anni fa, nel 1696. Ma perché proprio Clotoide? Perché ricorda il filo della vita di ciascuna persona, che la parca Cloto (non avendo di meglio da fare, in quei tempi in cui non c'era ancora la TV) andava avvolgendo da un fuso all'altro (i centri delle due spirali), scorrendo il tempo dell'esistenza umana.
Ma ecco un bravo laureando-ingegnere-civile del Politecnico, che sta proprio progettando un raccordo tra due archi di cerchio, uno esterno all'altro.
Avviciniamoci senza farci notare, spiamolo mentre disegna...
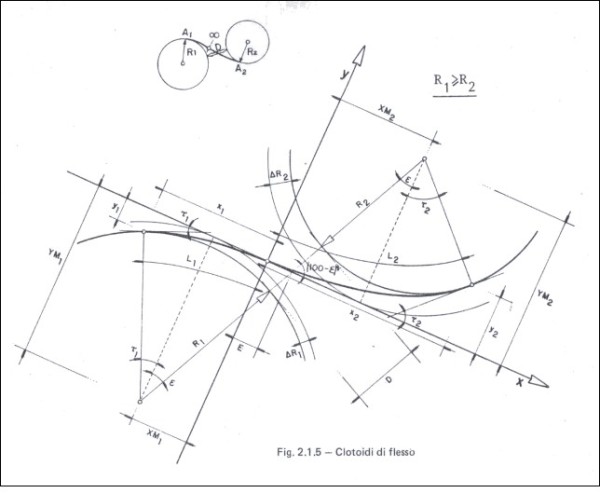
Non che ci si capisca molto... ma in fondo al foglio ha scritto “clotoidi di flesso” e si vede benissimo che i due cerchi sono collegati da una linea che inverte la sua curvatura in modo molto armonioso.
Questi ingegneri... Ma guarda un po', nel cestino della carta straccia, c'è qualcosa...

Ecco qua... una bella stirata...
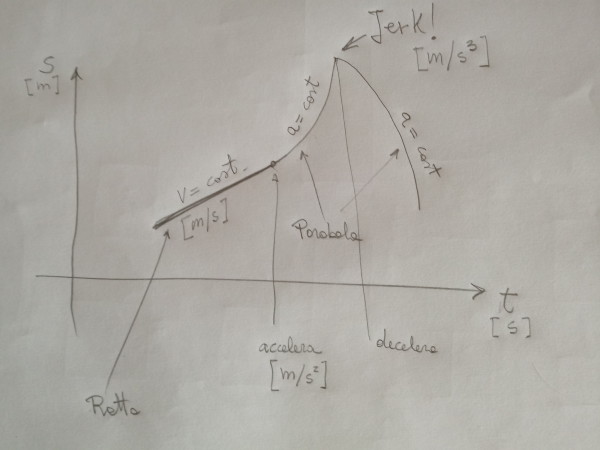
Sembra un grafico disegnato per chiarirsi le idee sulla curva oraria del moto. Dunque, moto rettilineo uniforme, una bella retta: spazi uguali in tempi uguali, poi qui accelera e lo spazio cresce con il quadrato del tempo, già, niente di strano, una parabola. E qui? Ancora una parabola sì, ma di decelerazione; una bella frenata, probabilmente ha visto il cartello dell'autovelox...
Comunque ha scritto Jerk ! con il punto esclamativo, qualcosa vorrà pur dire. E ci ha pure messo l'unità di misura [m/s3] certo, metri al secondo per secondo per secondo.
Avrà fatto di certo anche un grafico per l'accelerazione centripeta, cambiando i raggi di curvatura bruscamente, invece di raccordarli facendoli variare progressivamente lungo una clotoide, giusto per vedere le discontinuità che danno origine agli “strappi”, cioè a quella derivata terza dello spazio rispetto al tempo.
Va bene, vediamo cosa sta disegnando adesso...
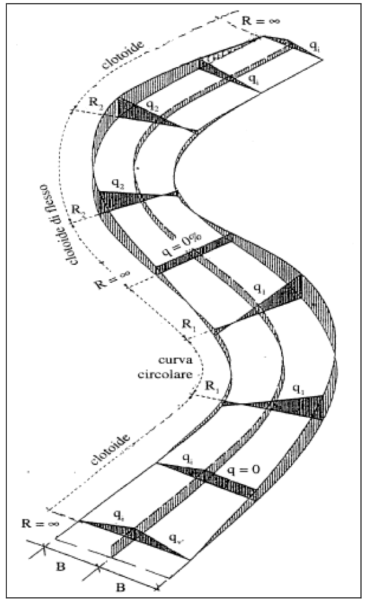
Ma, allora , è proprio fissato !
Questo, invece, deve essere il grafico "in bella" di quello che abbiamo recuperato dal cestino. Il ragazzo lo ha appeso alla parete di fronte alla scrivania, neanche fosse un Picasso.
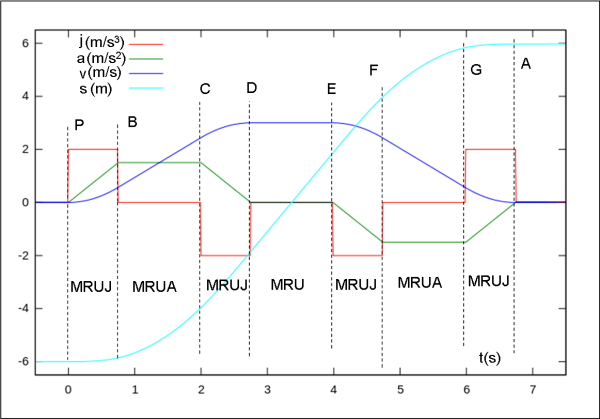
Questo grafico rappresenta l'andamento delle grandezze cinematiche durante uno spostamento da una stazione di partenza P ad una stazione di arrivo A, collegate da un lungo rettilineo, un binario ferroviario.
Per la verità è stato già discusso in un questo articolo, analizzando l'aspetto cinematico del moto, ma qui vogliamo darne una lettura un po' diversa che tocca da vicino le sensazioni dei viaggiatori.
L'asse orizzontale riporta il tempo, quello verticale i valori delle quattro grandezze: spazio, velocità, accelerazione e jerk, su una unica scala che di volta in volta va letta nella opportuna unità di misura (indicata in alto con il colore corrispondente alla funzione).
Visto che il tragitto del nostro treno è rettilineo, non dovremo affrontare la complicazione delle curve di raccordo a spirale di cui abbiamo parlato finora. Concentriamoci quindi su questo semplice modello.
I moti, applicati a oggetti dotati di massa (come sono appunto il treno e i passeggeri) danno origine a forze, ed altro ancora. Per essere più precisi esistono grandezze meccaniche collegate a velocità , accelerazione eccetera. Limitiamoci alle prime tre.
quantità di moto Q massa x velocità
forza F massa x accelerazione
strattone Y (yank) massa x "strappo" (jerk)
In una situazione reale il treno parte da fermo, con velocità zero (sarebbe scomodo per i passeggeri se non fosse così, perché dovrebbero prenderlo in corsa). Analogamente, alla stazione di arrivo, il treno si ferma, per far scendere comodamente i passeggeri e anche per non distruggere la stazione, nel caso sia terminale.
Quindi possiamo distinguere queste tre fasi: la partenza in cui ci si mette in moto, il percorso vero e proprio, in cui si copre la distanza più significativa, a velocità costante, senza accelerare né frenare, e infine l'arrivo, in cui si ritorna allo stato di quiete.
La fase centrale è certo quella meno interessante da un punto di vista dello studio del moto, si tratta di un semplice Moto Rettilineo Uniforme (MRU), in cui solo la velocità ha un valore diverso da zero, costante per tutto questo intervallo. E' un moto inerziale, in assenza di forze e strattoni, esiste solo la quantità di moto.
Separiamo allora i momenti più significativi di partenza e arrivo tracciandone i rispettivi grafici.
Alla Partenza
La condotta di guida alla partenza deve risultare confortevole per i passeggeri. Immaginatevi cosa succederebbe se, “di colpo”, il treno passasse dalla velocità zero alla velocità di crociera, diciamo 100 km/ora. Va bene, “di colpo” non significa niente, diciamo che in 2 secondi vi ritrovate a quella velocità. Una variazione di 100 km/ora in 2 secondi significa una accelerazione superiore a quella di una monoposto di F1 (che impiega 2,6 secondi). Corrisponde ad un valore di 13,8 m/s2, pari a 1,4 g. La concentrazione di questa accelerazione in quei due secondi genera un impulso di o,7 g/s che produce uno strappo repentino, il jerk.
Quei 0,7 g/s corrispondono a 6,9 m/s3, che è oltre 7 volte il limite massimo consentito, di 0,9 m/s3, per il comfort dei passeggeri "in piedi e senza appigli" a bordo di un mezzo .
Nel caso i passeggeri siano seduti, il jerk consentito non deve comunque superare 2 m/s3
Sul nostro treno, invece di essere schiacciati contro il sedile e magari subire il tipico “colpo di frusta”, come in un tamponamento, verrete gradualmente portati alla velocità giusta con una accelerazione lineare di valore più ragionevole, che agirà per un tempo più prolungato, diluendo lo "strattone" causato dal jerk, su quell'intervallo, ad una intensità accettabile.
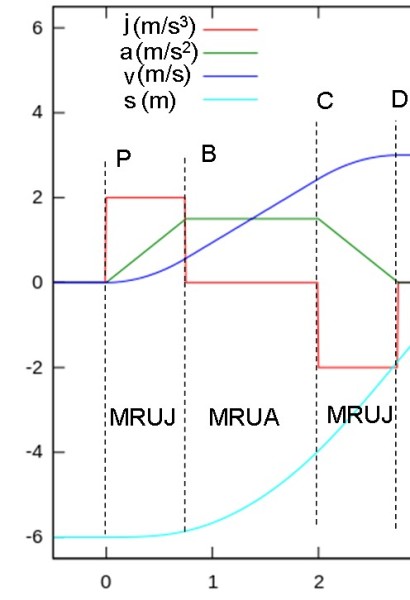
Osservando il grafico: Da P a B viene impressa una accelerazione (linea verde) che cresce linearmente fino a raggiungere un valore massimo in B. Parimenti la velocità ( linea blu), essendo l'integrale della accelerazione, cresce con un andamento quadratico e lo spazio, integrale della velocità (linea azzurra), aumenta con una legge cubica.
L'aumento progressivo della accelerazione ha anche l'effetto di produrre il jerk, (linea rossa), una cosa inevitabile ma il cui effetto può essere limitato, come abbiamo visto, controllando la legge di variazione della accelerazione. L'impulso a gradino ha la durata della rampa di accelerazione e una ampiezza che , nella scala del disegno, è allineata al valore di 2 m/s3 , proprio il limite del valore raccomandato nel caso di passeggeri seduti.
Ma, a parte questo particolare, che non avrete mancato di notare, ciò che interessa è capire come evolve la manovra di avviamento. Ad un certo punto, superato B, è necessario smettere di far crescere l'accelerazione, cioè mantenere un valore costante per non oltrepassare la velocità di crociera che vogliamo mantenere durante il viaggio. Siamo quindi nell'intervallo tra B e C.
Se nel precedente intervallo PB eravamo giunti alla conclusione che il jerk era costante (abbiamo usato la sigla MRUJ per significare che si tratta di un Moto Rettilineo Uniformemente Jerkato) ora, non crescendo più l'accelerazione, il jerk si annullerà (la derivata di una costante è zero) e passeremo ad un Moto Rettilineo Uniformemente Accelerato (MRUA), molto più familiare alle nostre orecchie. Quindi tra B e C, in costanza di accelerazione, la velocità continuerà ad aumentare, ma con legge lineare e non più quadratica. Lo spazio crescerà invece con legge quadratica e non più cubica.
Ebbene, cosa ci manca per concludere questo transitorio? Chiaramente dobbiamo fissare definitivamente la velocità al valore di crociera, rendendola costante.
Questo avverrà nell'intervallo tra C e D. Se mantenessimo costante l'accelerazione la velocità continuerebbe a crescere oltre il desiderato. Occorre quindi ridurre l'accelerazione fino a portarla a zero, nel momento D, quando la velocità raggiunta è proprio quella che vogliamo mantenere.
Riportare l'accelerazione a zero in modo graduale significa generare una rampa in discesa, la cui derivata, il jerk, sarà un gradino in discesa. Avremo di nuovo uno strappo, ma controllato entro valori accettabili, opposto al precedente. I passeggeri lo avvertiranno come una spinta in avanti, nel senso del moto, per tutto il periodo in cui l'accelerazione è variabile. In questa fase siamo tornati ad una modalità di moto rettilineo MRUJ.
Ed eccoci finalmente in movimento a velocità costante, senza accelerazioni e senza jerk tranquillamente seduti per il tempo del viaggio che ci separa dall'arrivo.
Lo spazio che abbiamo coperto in questa ultima fase del transitorio di partenza è cresciuto con una legge cubica, ma da ora all'arrivo, crescerà in modo lineare, data la costanza della velocità.
Come detto non c'è nulla di particolare nella fase centrale del nostro trasferimento che avviene a velocità costante, quindi passiamo direttamente a vedere cosa succede a fine corsa, al momento dell'arrivo.
All'arrivo
Siamo prossimi alla conclusione del viaggio. Ora il treno dovrà “essere convinto” ad entrare in stazione con il dovuto garbo, alla minima velocità sufficiente per raggiungere il punto esatto in cui fermarsi.
Il tutto, naturalmente dovrà rispettare, come alla partenza i criteri di comfort per i passeggeri. Vediamo il grafico di questa fase finale.
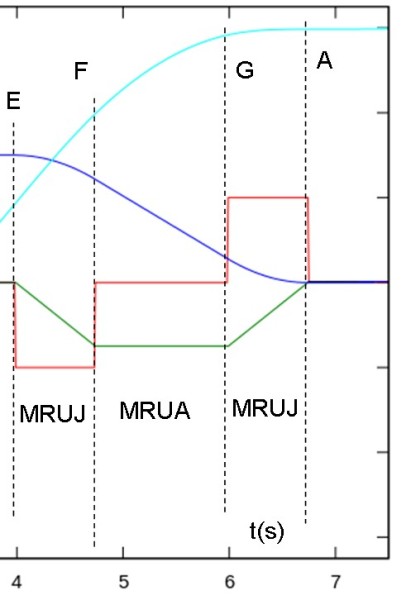
Non potete non avere notato la simmetria tra questo grafico e quello della partenza. In particolare la velocità, la linea blu, si riduce modellandosi in modo speculare sulla medesima forma con cui era cresciuta all'inizio, come i due versanti di una stessa onda.
Ma analizziamo i vari intervalli per meglio comprendere la logica del controllo.
Con un anticipo che si può correlare alla distanza che manca all'arrivo, nel punto E, si inizia una manovra di frenatura, ossia di decelerazione o accelerazione negativa. Non può mancare il jerk associato a questa variazione di accelerazione, da zero ad un valore linearmente decrescente. Sarà un jerk negativo, quindi, uno di quelli che ci fanno sentire spinti in avanti. Ma la spinta non sarà troppo accentuata, se l'accelerazione è regolata bene, e durerà da E a F. L'effetto sulla velocità è ovvio, calerà con una legge quadratica. Lo spazio invece continuerà ad aumentare, ma con una crescita cubica. Il tipo di moto in questa fase, con un jerk costante, è evidentemente MRUJ.
Ora si tratta di dosare la frenata, fermandosi ad un certo livello, costante , prima di ridurla in modo progressivo. Passeremo quindi attraverso una fase intermedia, che potremmo chiamare di stabilizzazione, tra il punto F e il punto G, in cui non aumentiamo l'efffetto frenante ma lo manteniamo ad un valore costante. In questo modo il jerk si annulla. La velocità si riduce con andamento lineare , lo spazio continua a crescere con legge quadratica. Il moto si qualifica come MRUA.
Se non avessimo seguito questa procedura, con cui abbiamo attraversato una fase di frenatura costante, non avremmo interposto alcuna pausa tra il jerk negativo in EF e il jerk positivo di cui ora parleremo. Risultato? Una inversione repentina, da strappo in avanti, a strappo all'indietro, con conseguenze deleterie per l'incolumità dei passeggeri.
Eccoci giunti all'ultima manovra della nostra meditata strategia. Siamo al punto G e ci muoviamo verso A, il traguardo finale. Occorre riportare a zero la decelerazione, ossia ridurre linearmente l'effetto frenante. Questo comporta l'ultimo jerk del nostro viaggio, un (lieve) strappo all'indietro, tra G ed A.
Siamo a arrivati, con velocità zero, in corrispondenza del capolinea.
Questo ultimo tratto è stato coperto con un moto, ormai è chiaro a tutti, di tipo MRUJ.
Il viaggio è terminato, non dimenticate il bagaglio a mano.

L'avventura del jerk continua QUI







7 commenti
Veramente interessante....Grazie !!!
Grazie a te, Franco per l'attenzione e il commento. Non perdere la prossima puntata, mi raccomando....
Il gioco di derivate si risolve in termini semplici partendo dalla considerazione che
le manovre siano "lisce". Ma in matematica una curva liscia è una funzione continua e derivabile infinite volte.
Inoltre l'accelerazione deve essere limitata e graduale da 0 al suo massimo e poi fino a 0.
Una ottima curva limitata e "liscia" con queste caratteristiche è la funzione coseno.
In particolare la funzione accelerazione
sarà nulla per t=0 ed anche in t=2 pi. Inoltre la sua derivata è nulla agli estremi. Notare quanto è ... liscia.
Volendo ottenere il jerk necessario dobbiamo derivare l'accelerazione
Procedendo in senso inverso, per trovare la velocità integriamo l'accelerazione:
integrando ancora si ottiene lo spazio percorso:
x(t) = x(0) + v0 t + 1/2 t^2 + cos(t)
) =0 , accelerazione iniziale nulla
=0 , accelerazione iniziale nulla
Adesso imponiamo i vincoli:
x(0) =0 ,origine dello spazio =0
v(0) =0 ,partenza da fermo
v(t)max= Vmax da ottenersi per t=2 pi , alla fine della manovra di accelerazione
a(t)max= da minimizzare in tutto l'intervallo
Si ottiene
X(t) = 1/2 t^2 +cos(t)
) = t -sin(t)
= t -sin(t)
) = 1-cos(t)
= 1-cos(t)
) = sin(t)
= sin(t)
La velocità massima raggiunta sarà) =
= &space;=&space;2&space;\pi)
L'accelerazione massima è limitata quindi dobbiamo trovare il massimo della funzione
derivando ed uguagliando a zero
D () ) =0
) =0
) =0 ovvero sin(t) =0
=0 ovvero sin(t) =0
ciò avviene dove il jerk si annulla
quindi la massima accelerazione si avrà per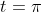
 )= 2.
)= 2.
e vale 1 - cos(
Per esempio, se desideriamo un' accelerazione massima pari a 0.6 , corrisponda un tempo pari a 2/0.6 = 3.3 secondi.
corrisponda un tempo pari a 2/0.6 = 3.3 secondi.
dobbiamo imporre che a
In tutto questo giro c' è una variabile che non è liscia, cioè non è derivabile nel punto in cui passa da zero al valore seno : è il jerk . Potremmo continuare imponendo che anche il jerk sia derivabile in zero.
buon viaggio e speriamo che vada tutto.... liscio.
Grazie, Leandro, un approfondimento molto interessante.
Poi, naturalmente, se compare all'improvviso un gregge di pecore sui binari e occorre frenare di colpo, non sempre si riuscirà a farlo sinusoidalmente... Pazienza.
Nel grafico appeso alla parete dal ragazzo, neanche fosse un Picasso, la linea blu della velocità corrisponde esattamente, se fossimo su un aereo, anche all'andamento della quota di un volo completo: decollo con relativa salita, rotta, discesa con relativo atterraggio. Così per me diventa ancora più esemplificativo del treno.
Grazie Vincenzo, mi hai fatto conoscere una nuova fetta di analisi di cui nessuno mi aveva mai parlato. Neppure il mio stimatissimo vecchio docente Zwirner (istituzioni matematiche per chimici a Padova, fine anni 60). Ora, a fine vita, scopro sempre di più quanto sono ignorante
Scusa Maurizio, sono abituato con Vincenzo, ho visto ora che l'autore invece sei tu, Bernardi.
Altrettanto chiaro! Ed è un bel complimento
Caro Alberto, certo che è un bel complimento ! Grazie.