Matematizziamo il nastro di Möbius ,parte 8°: Il cilindro e il nastro.***
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica
Vogliamo adesso occuparci di superfici. In topologia possiamo costruire nuovi spazi usando la topologia quoziente.Come vedremo, la descrizione dello spazio quoziente è più semplice rispetto alla descrizione analitica della superficie immersa.
Le funzioni quoziente,richiami.
Gli spazi che vogliamo costruire in modo astratto con la topologia quoziente, quasi sempre sono già noti in , dove hanno una loro rappresentazione analitica. Non sono chiaramente lo stesso spazio; da una parte abbiamo la topologia quoziente,definita in modo astratto, dall'altra la topologia definita in
. Nell'esempio delle funzioni quoziente, il segmento con gli estremi incollati non è proprio un cerchio in
, però è omemomorfo a tale cerchio. Questo è il concetto che vorrei chiarire bene.
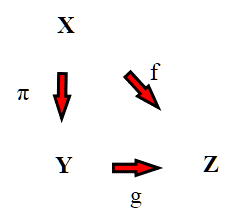
Abbiamo dunque il nostro spazio topologico X e una relazione di equivalenza che ci permette di costruire il nostro spazio quoziente ; abbiamo poi al solito, la proiezione
che ad ogni elemento di X associa la propria classe.
Si dice che una funzione f : X → Z discende al quoziente se esiste g : Y → Z tale che f = g ◦ π. La funzione g è detta funzione quoziente di f. Si verifica che una funzione f : X → Z discende al quoziente se assume lo stesso valore
su tutti i punti di una stessa classe di equivalenza, ovvero se e solo se f soddisfa la proprietà:
* .
Se esiste una funzione con questa caratteristica, possiamo definire g([p]) = f(p) e la proprietà * garantisce che è ben definita (ossia indipendente dal rappresentante della classe [p]).
Esempi di superfici
Mettiamoci ora nel piano, e consideriamo un quadrato . Questo quadrato sarà la nostra striscia di gomma, o di carta, da incollare nei bordi. E' infatti facile,per costruire per esempio un cilindro, incollare due lati opposti di un quadrato, mantenendo lo stesso orientamento sui lati.Noi però dobbiamo fare queste operazioni di incollatura topologicamente. Sembra impossibile che una cosa così semplice sia il punto di partenza per costruzioni di spazi molto complicati concettualmente.
Il cilindro
Partiamo dalla figura più semplice, il cilindro, o meglio la superficie laterale del cilindro. Prendiamo dunque il nostro foglio di gomma e incolliamo i due bordi opposti. Matematicamente questo corrisponde a definire una relazione di equivalenza su un quadrato X, in modo di considerare lo stesso punto i punti equivalenti. Una relazione d'equivalenza definita sul quadrato X potrebbe essere questa:(s, t) ∼ (s′, t′) ⇐⇒ (s, t) = (s′, t′) oppure {s, s′} = {0, 1} e t = t′
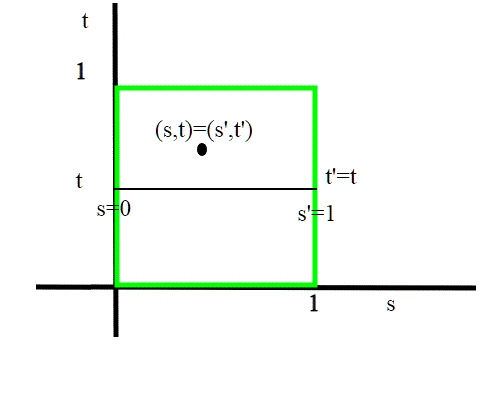
I punti interni al quadrato sono equivalenti solo a se stessi, mentre il lato sinistro verticale viene ad essere identificato dalla relazione con quello destro verticale. Infatti, (0, t) ∼ (1, t).

Riassumendo: X è un quadrato, mentre lo spazio quoziente è intuitivamente un cilindro C. Siamo quindi passati dal piano allo spazio perchè per piegare il foglio dobbiamo uscire dal piano. Vorrei riflettere più a fondo su questo fatto.
Intuitivamente, visto che possiamo farlo anche nella realtà, sappiamo che incollando in tal modo i lati di un quadrato costruiamo un cilindro.Nella realtà topologica, tale spazio non è proprio un cilindro, ovvero quello che conosciamo da sempre. Dobbiamo usare un linguaggio topologico. Lo spazio è omeomorfo al cilindro C.
Proviamo a costruire il cilindro in altro modo, sempre con la topologia quoziente, per approfondire questo fatto con le funzioni quoziente.
Consideriamo il rettangolo del piano X=[0,] x [0,1]. Su X consideriamo la relazione di equivalenza:
(tutti gli altri punti sono equivalenti solo a se stessi)
Dal passaggio al quoziente otteniamo lo spazio . Pensiamo adesso al cilindro che conosciamo ; la sua equazione parametrica nello spazio sarà:
f:: questo è proprio il cilindro C. f:X=[0,
] x [0,1]--->Z dove Z è un sottoinsieme di
.
Quello che vogliamo dimostrare, è che esiste un omeomorfismo g: . Verifichiamo la proprietà *:
sappiamo che ;
f(0,v)=(cos0,sen0,v)=(1,0,v); f(2π,v)=(cos2π,sen2π,v)=(1,0,v)
quindi f(0,v)=f(2π,v).
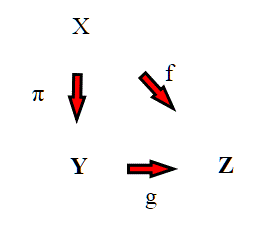
f è continua, quindi per la proprietà fondamentale del quoziente anche g è continua. g è inoltre iniettiva. Infatti è definita come g([p])=f(p); se g([p])=g([q]), allora f(p)=f(q) ma questo succede solo se .
Possiamo allora applicare il nostro teorema necessario:
Sia g : X -->Y un’applicazione continua e biunivoca. Se Y è compatto e Z è di Hausdorff allora g è un omeomorfismo.
g è continua e biunivoca. E' definita su Y che è un compatto, essendo immagine del compatto [0,] x [0,1] tramite
. Z (il cilindro) è di Hausdorff, essendo un sottospazio di
. Quindi g è un omemomorfismo. Il cilindro costruito incollando i due lati di un quadrato è quindi omemorfo al cilindro immerso in
, con espressione analitica data da
f: .
Il nastro di Möbius
Come già visto negli articoli di Maurizio, per costruire il nastro dobbiamo incollare i lati opposti di una striscia dopo averne ruotato uno di 180 gradi.

Se prendiamo come per il cilindro il quadrato , possiamo considerare su di esso la relazione di equivalenza (s, t) ∼ (s′, t′) ⇐⇒ (s, t) = (s′, t′) oppure {s, s′} = {0, 1} e t = 1 − t′.
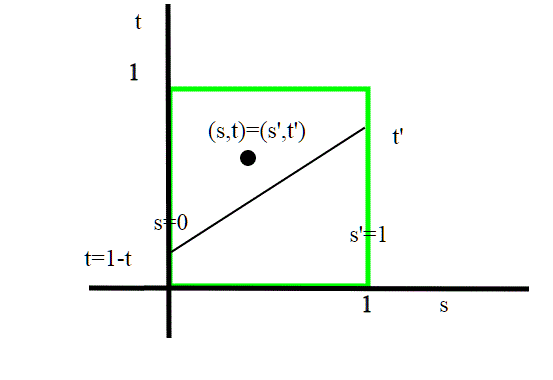
I punti interni al quadrato sono equivalenti a se stessi come nel caso del cilindro, mentre in questo caso (1, t) ∼ (0, 1−t).
La figura che intuitivamente si ottiene è proprio il nastro di Möbius:
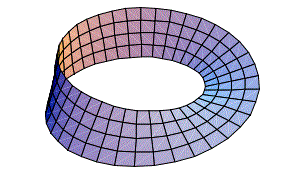
Esistono rappresentazioni parametriche del nastro in , ma sono però molto più complesse di quelle del cilindro. Anche per esse si può dimostrare l'omeomorfismo con lo spazio quoziente generato in modo astratto tramite incollamento. Per ora non lo facciamo; prima bisognerà ricavare una espressione parametrica per il nastro nello spazio.
Si può dimostrare che sia il cilindro che il nastro sono due varietà topologiche; riprendo adesso parte dell'articolo per spiegare una differenza fondamentale fra le due superfici l'orientabilità:
Riprendiamo in mano il nostro cilindro con due bordi. Intuitivamente non facciamo nessuna fatica a pensare che il cilindro abbia un "dentro" e un "fuori" ovvero due facce.

E' possibile colorare la superficie del cilindro con due colori diversi, uno per la parte esterna e uno per la parte interna. Si dice in questo caso che la superficie del cilindro è orientabile. Questa è la definizione "antica" di superficie orientabile. In pratica non è possibile passare da una faccia all'altra senza attraversare il bordo o bucando la superficie. Nel quiz art-attak di Maurizio abbiamo già visto un esempio di superficie non orientabile, che è proprio il nastro di MÖBIUS; nell' esempio reale del quiz abbiamo toccato con mano l'impossibilità di colorare il nastro con due colori diversi, infatti se proviamo a colorare il nastro partendo da un suo punto qualsiasi, finiamo con il colorare tutto il nastro senza attraversare il bordo.

A questo punto, i matematici dicono semplicemente: una superficie non è orientabile se e solo se contiene un nastro di MÖBIUS . Questa è una definizione moderna di orientabilità.






2 commenti
Passo dopo passo , prosegue un percorso che "orienta" il lettore alla comprensione di una materia che personalmente trovo affascinante.
Grazie Umberto!
grazie a te