Un simpatico problema geometrico che mette in gioco i percorsi su una superficie cilindrica e che vuole dimostrare come spesso e volentieri una soluzione apparentemente immediata  nasconde un approccio matematicamente più complesso. Come dire che la fretta è una cattiva consigliera.

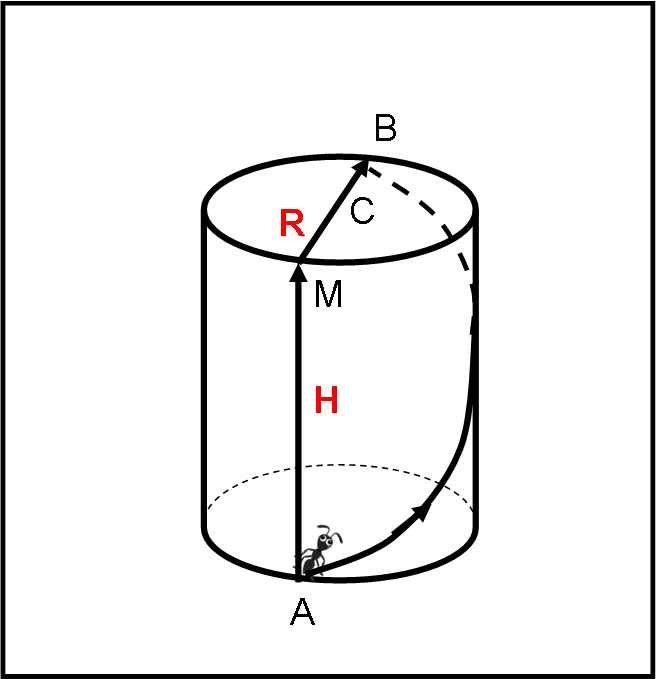
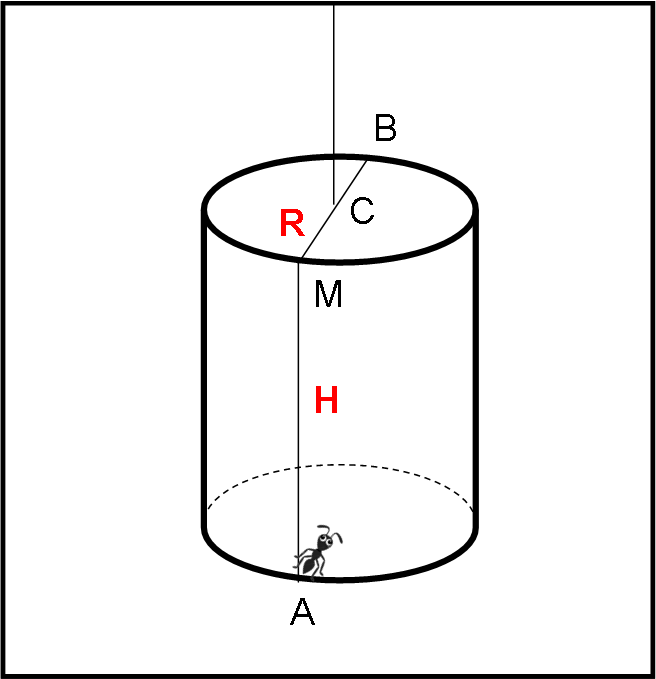
Per il nostro esperimento sono necessari un barattolo chiuso di forma cilindrica che immaginiamo sospeso attraverso una corda sottilissima. La configurazione vuole solo dire che qualsiasi percorso lungo l’esterno del barattolo è possibile. Il secondo personaggio è una formica che si trova nel punto A. La domanda è molto semplice: “Qual è il percorso più breve che deve fare la formica per raggiungere il punto B che si trova nella parte superiore ed è simmetrico ad A rispetto al centro del barattolo”.

Sia R = CM = CB il raggio delle basi del cilindro e H = MA la sua altezza, come indicato in figura.

 

E' facile valutare rapidamente due casi estremi e il tutto appare  piuttosto semplice. La fretta, però, è cattiva consigliera ed è necessario che la formica ragioni un po’ più a fondo sulla questione (e non solo lei).

La nostra formica è piuttosto intelligente, ma è anche molto pigra e non vuole assolutamente tentare una strada che la costringerà a fare un percorso più lungo. Perciò, prima di muoversi, studia bene la situazione.

Lei sa benissimo che un cilindro ha una specie di falsa “curvatura”, dato che su di lui valgono le regole della geometria euclidea. In altre parole, basta srotolarlo e tutto ciò che si disegna sopra è tale e quale a ciò che si disegna su un piano. Ciò, ovviamente non sarebbe possibile se fossimo su una sfera (come abbiamo imparato bene QUI ).

Senza ancora srotolarlo si possono comunque notare due strade molto interessanti: la prima è quella di salire fino a M e poi attraversare il coperchio fino a B. La seconda è quella di percorrere una specie di elica che la porti in B lungo la parte laterale del barattolo, come rappresentato in Fig. 1.

La formica decide di rappresentare la situazione immaginando di srotolare il cilindro, come riportato in Fig. 2.  Le due soluzioni, decisamente diverse, si vedono molto meglio.  Il punto B appartiene sia alla faccia circolare superiore, ma anche alla parte superiore della superficie laterale del cilindro.

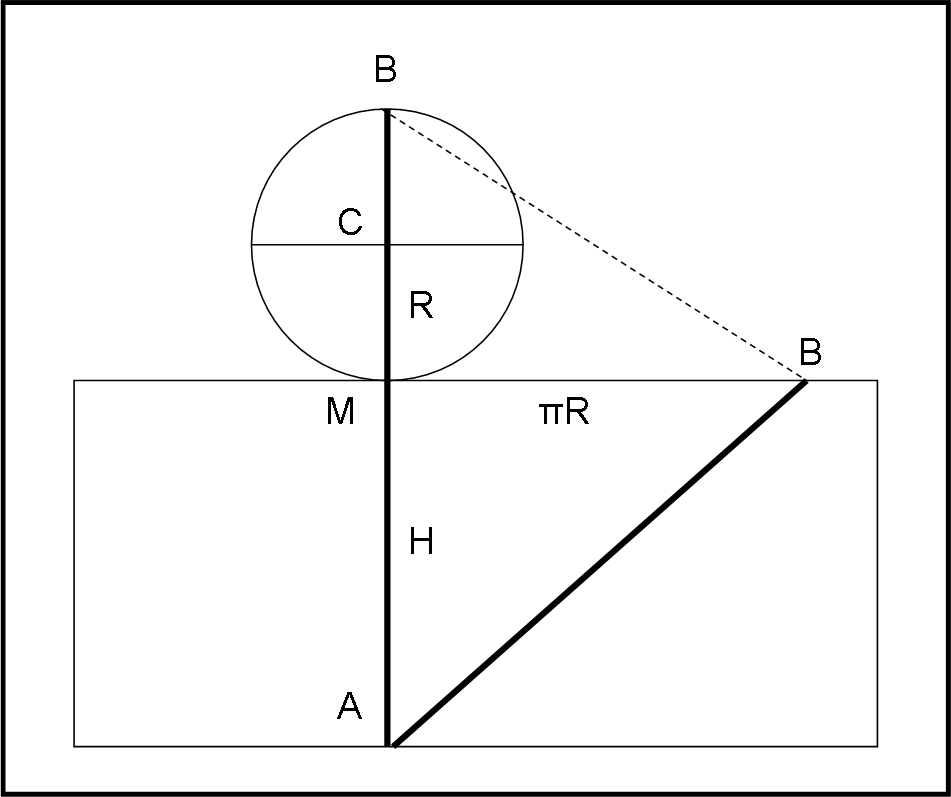
La formica è molto indecisa e forse sarebbe spinta a fare il percorso diagonale AB (che ora appare com’è intrinsecamente, ossia del tutto rettilineo). Però preferisce controllare attraverso qualche calcoletto semplice semplice. Sta, infatti, pensando che la soluzione migliore dipenda molto dall’altezza H e dal raggio R: Perché allora non scrivere una relazione che leghi il primo percorso al secondo e vedere cosa succede?

Nel caso del percorso AM e MB si ha:

s₁ = H + 2R

Nel caso del percorso “obliquo” AB, bisogna considerare la lunghezza orizzontale e quella verticale. La seconda è ovviamente H, mentre la prima è esattamente la metà della circonferenza, ossia πR. Dal triangolo rettangolo AMB si ha (teorema di Pitagora):

s₂ = (H² + (πR)²)^1/2

Dato che il cilindro è quello che è (ossia H e R sono quelli che sono), alla formica non resta che confrontare le due soluzioni, vedendo quando sono uguali e se possono esserlo. Dopo di che vedrà se invece dell’uguale, nel caso in oggetto, ossia per un certo H e per un certo R, il segno  dovrà essere sostituito dal segno maggiore o minore.

s₁ = s₂

ossia

H + 2R = (H² + (πR)²)^1/2        …. (1)

 Alla formica piacciono poco le radici quadrate e preferisce farla sparire elevando a quadrato entrambi i membri:

H² + 4R² + 4HR = H² + (πR)²

Semplificando e spostando, ottiene:

4HR = (πR)² - 4R²

4HR = R²(π² – 4)

4H = R(π² – 4)

H/R = (π² – 4)/4

H/R = π²/4 – 1 ≈ 1.467    …. (2)

Cosa dice questo risultato? Solo e soltanto che se H è maggiore di 1.467 R, la via migliore è quella del percorso diagonale (il primo percorso è maggiore del secondo, come dice la (1)). Se, invece H è minore di 1.467 R, la via migliore è la prima. Se H fosse proprio uguale a 1.467 R, le due strade sarebbero identiche.

Alla formica non rimane che misurare H e R per sapere che strada scegliere. Cosa alquanto sciocca, dato che per misurare queste grandezze dovrebbe raggiungere B in ogni modo… Tuttavia, ammettendo che la formica sappia fin dall’inizio i valori di H e R, la sua scelta sarebbe facilissima sulla base della (2).

La formica sa quanto valgono H e R e sta per mettersi in moto. Proprio in quel momento arriva un piccolo scarabeo che sembra veramente uno studioso (porta anche gli occhiali) e dice alla formica: “Stai attenta, cara amica. Tu hai preso una decisione trascurando la logica matematica. Sei arrivata a una conclusione senza valutare veramente tutte le variabili del problema. E’ un po’ come se tu avessi scelto la soluzione basandoti solo sui casi estremi, senza valutare le possibilità intermedie.”

Lo scarabeo ha perfettamente ragione! Le vere variabili non sono H e R (o H/R per semplificare), dato che esse definiscono solo due casi limite del percorso: o bianco o nero e tutto il resto viene trascurato.

Facciamo un esempio molto banale e tracciamo, in Fig. 3, una certa funzione y = f(x), limitata in un certo intervallo x₁ - x₂. Essa contiene sia H che R e assume una forma diversa a seconda che H/R abbia un certo valore o un altro. Comportandoci come la formica noi abbiamo solo analizzato gli ESTREMI di questa funzione, ossia quelli corrispondenti a x₁ e x₂. Per certi valori di H/R vince il primo estremo; per altri valori vince il secondo estremo. Per un valore ben determinato c’è una parità.

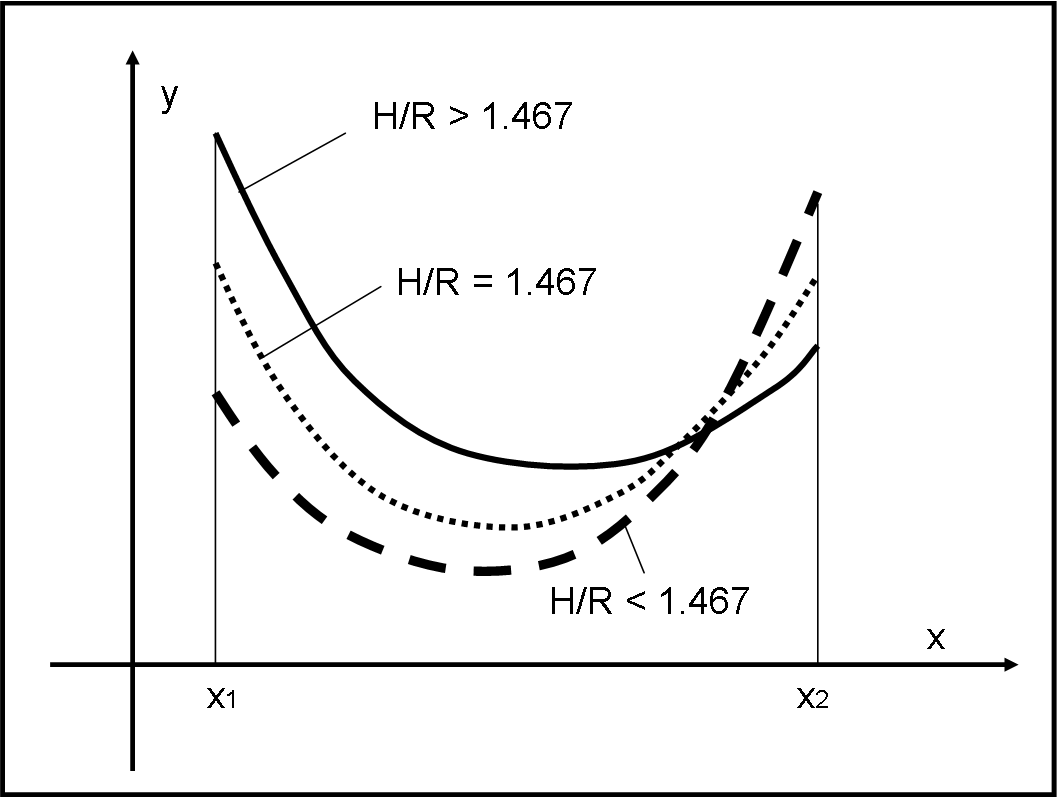
Qual è il grave errore che è stato fatto? Non abbiamo descritto l’intera funzione f(x) che potrebbe avere un minimo al suo interno, un minimo più basso del valore assunto agli estremi. In altre parole, non abbiamo studiato la funzione f(x) nell’intervallo x1- x2 per un valore FISSO di H/R.

Ma se H/R è fisso, qual è la nuova variabile x che dobbiamo considerare (cosa che non abbiamo fatto)? Bene, cominciamo col dire che la y non è altro che lo spazio s da percorrere. La x, invece, si nota costruendo la Fig. 4. Come si vede vi è tutta una serie di possibili percorsi (fissato il rapporto H/R) che può essere seguito dalla formica ed essi dipendono dall’angolo φ. Considerando solo gli estremi, daremmo una soluzione che non tiene in conto della infinita varietà di percorsi ottenibili per φ che varia tra 0 e π.

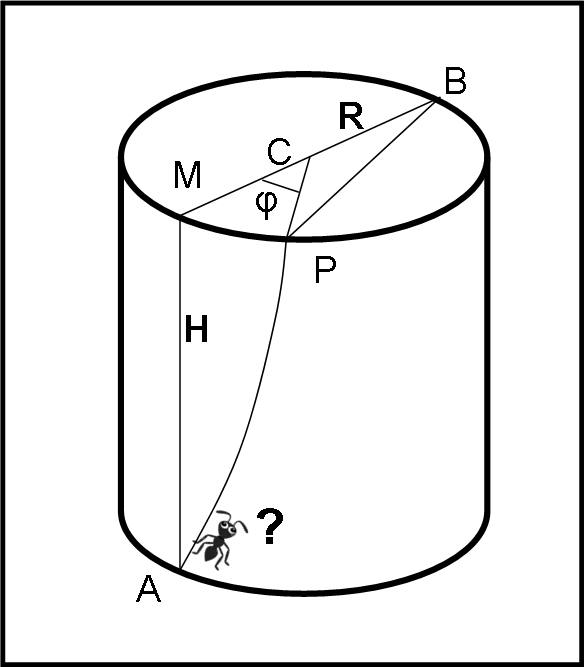
Possiamo anche costruire la Fig. 5 con il cilindro srotolato e vedere la situazione.

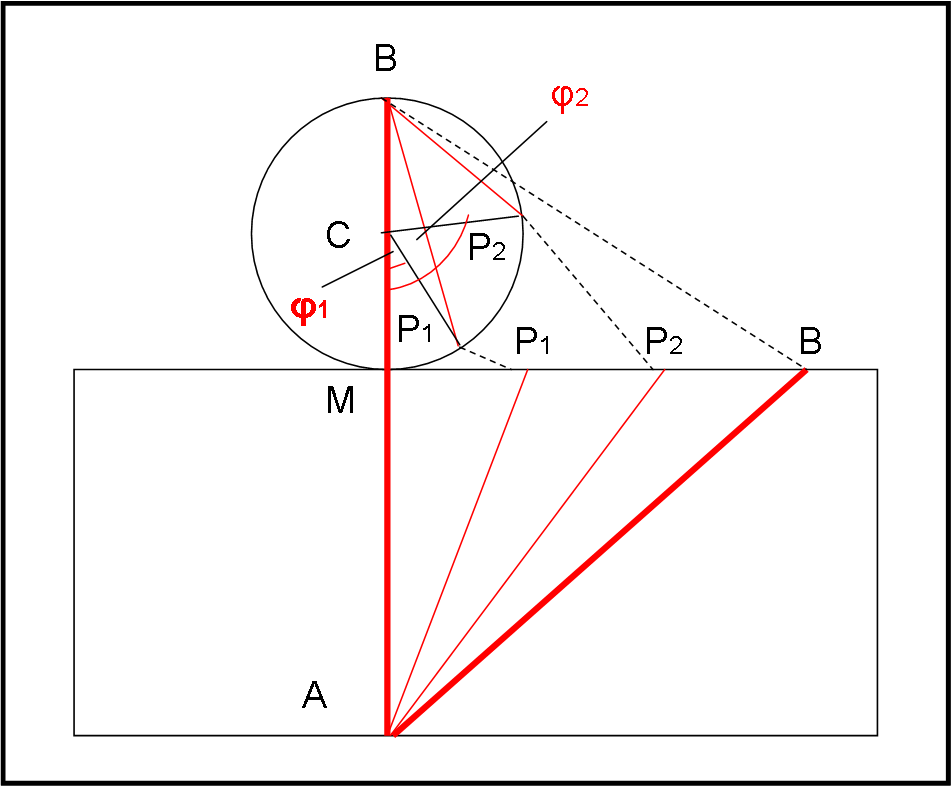
Ricapitolando, la formica ha solo deciso tra i due percorsi segnati in grassetto, trascurando del tutto tutti i percorsi intermedi che potrebbero benissimo portare a una distanza minore.

Siamo arrivati a un punto decisivo. Per risolvere veramente il problema si deve  costruire la funzione s = s(φ) per un certo valore (considerato noto) di H/R e, soprattutto, vedere se ha un minimo nell’intervallo tra φ = 0 e φ = π.

Questo tipo di errore “formale”, ma anche molto pratico, capita molto più spesso di quanto si possa pensare… Questo esempio  vuole soprattutto insegnarci a non sbagliare l’approccio matematico per fretta o per aver trascurato una variabile fondamentale.

Vi dico subito che la soluzione dell’esempio fatto presuppone una buona conoscenza dello studio di funzioni  e -forse- anche una dose di intuito e ragionamento in più… Chi vuole  può provare a svilupparlo e a inserirlo nei commenti. Il vero scopo didattico dell'articolo è già stato ottenuto.

 

QUI la soluzione, insieme a divagazioni semiserie (più serie che semi) sulla divisione per zero

 

Vi è piaciuto calcolare questo percorso? QUI ne troverete altri!