Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica.

 

A volte, in fisica, vi sono fenomeni che possono sembrare, a prima vista, controintuitivi. Ne presentiamo uno che è una specie di classico in tal senso...

Ricordate i vecchi rocchetti per il filo da cucito? Bene, abbiamo solo bisogno di uno di loro. Lo proponiamo come domanda, ma, vi prego, di cercare di dare la risposta senza passare alla prova pratica (lo potete fare dopo…).

Nella Fig. 1 vi è una visione schematica del rocchetto attorno a cui è avvolto del filo. Il raggio della parte con il filo sia R, mentre il raggio delle due ruote esterne sia r > R. Il gioco sta tutto nel tirare il filo con una certa forza F, di modulo costante.

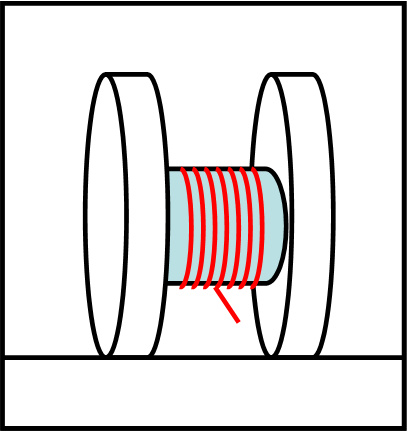
La variabile è quindi l’angolo ϑ che il filo forma con la linea orizzontale, come mostrato in Fig. 2 (il rocchetto è visto di lato). Ricordiamoci che il rocchetto rotola senza scivolare.

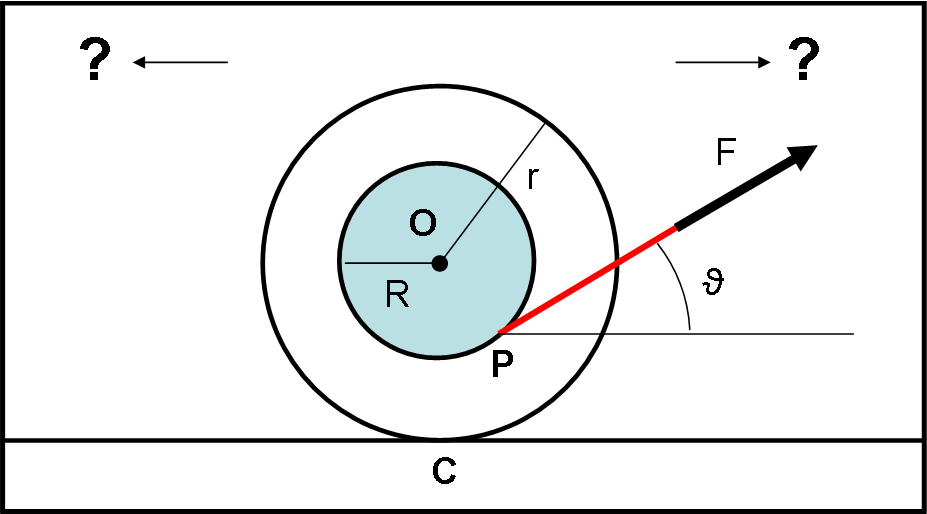
Vi sono vari metodi per risolvere il problema e dimostrare cosa fa il rocchetto. Noi siamo interessati al concetto e non a tanti calcoli, per cui chiedo soltanto da che parte si muove il rocchetto e se la sua direzione cambia a seconda del valore dell’angolo ϑ. La dimostrazione ha bisogno soltanto di un unico concetto grafico e di una giusta definizione del problema (niente formule quindi… ma un paio di figure, al massimo).

 

A questo punto potete decidere se dare la vostra risposta nei commenti oppure continuare a leggere.

 

Il problema si ricollega in qualche modo a quello più semplice della “carta igienica” e a quello più complesso dello “yo-yo”.

L’unico modo che ha il rocchetto di muoversi (non può strisciare) è quello di rotolare. L’unico punto attorno a cui effettuare il rotolamento è il punto di contatto con il piano d’appoggio, ossia C. E’, però, una rotazione istantanea, dato che C è costretto a lasciare il piano d’appoggio e venire sostituito con un punto C’, immediatamente successivo, della ruota più larga, o a sinistra o a destra di C, a seconda del verso del moto.

Per capire meglio la situazione, basta sostituire il rocchetto con una serie infinita di aste rigide fissate nel centro O come mostrato in Fig. 1. L’asta rigida corrispondente al punto di contatto C (al tempo t) ruota sotto l’azione della forza F e viene sostituita (al tempo t’ > t) dall’asta che ha come punto di contatto istantaneo C’. In parole ancora più semplici: l’asta rigida istantanea CO “cade” verso destra per effetto della forza F che la fa ruotare in quella direzione. La caduta viene bloccata dall’asta rigida e solidale C’O che ne prende il posto. Come conseguenza l’intero sistema si muove verso destra, effettuando nel contempo una rotazione attorno a O.

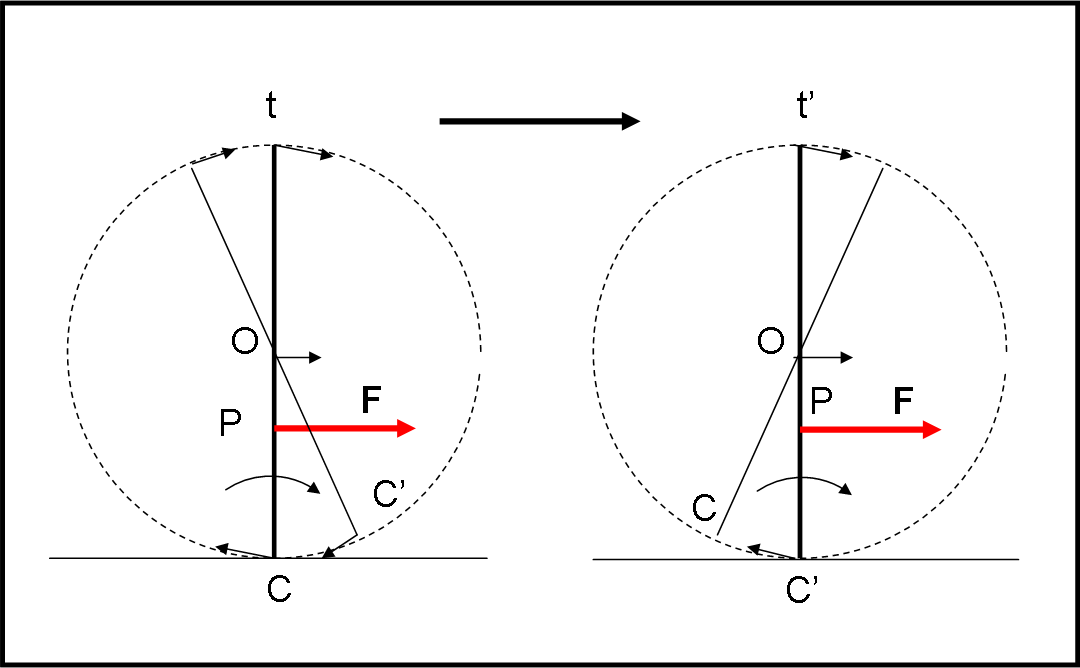
Ho cercato sul web una figura che rappresentasse una ruota con tanti piedi (sono sicuro di averla vista varie volte), ma non l’ho trovata… Ne ho fatto, quindi, uno schema che sia abbastanza indicativo in Fig. 2.

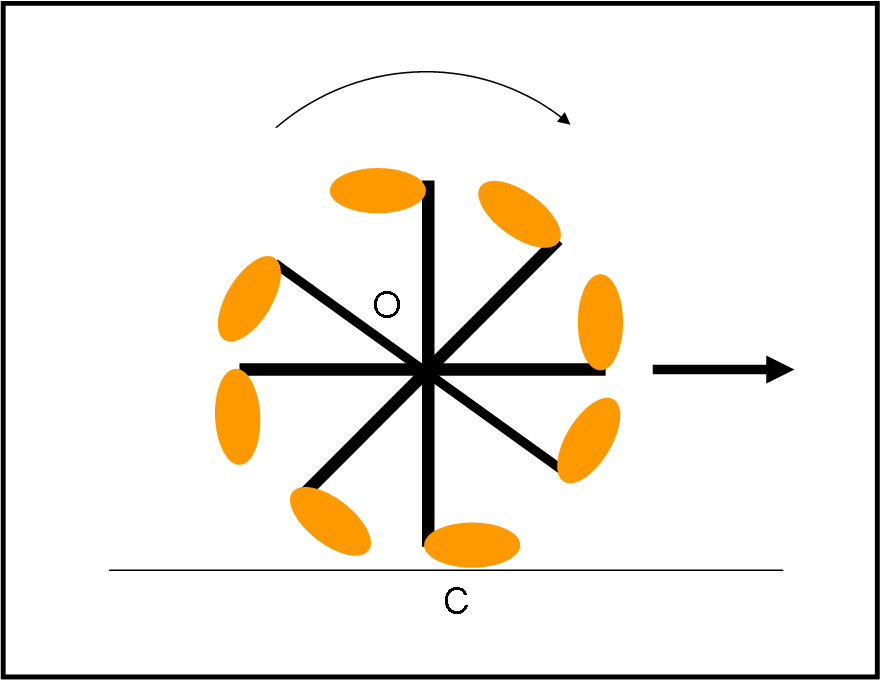
Se agisce una forza diretta verso destra, la ruota si sposta verso quella direzione dato che il centro di rotazione istantanea è C.  La forza è applicata in modo da causare una rotazione istantanea attorno a C. Tuttavia, dato che la struttura è ancorata in O e perfettamente simmetrica, lo spostamento verso destra si somma a una rotazione attorno a O.

Lasciamo da parte ruote e piedi e torniamo a qualcosa di un po’ più fisico. Ricordando il momento di una forza e il prodotto vettoriale (parte finale di questo approfondimento). Il succo di tutto il discorso è schematizzato in Fig. 3.

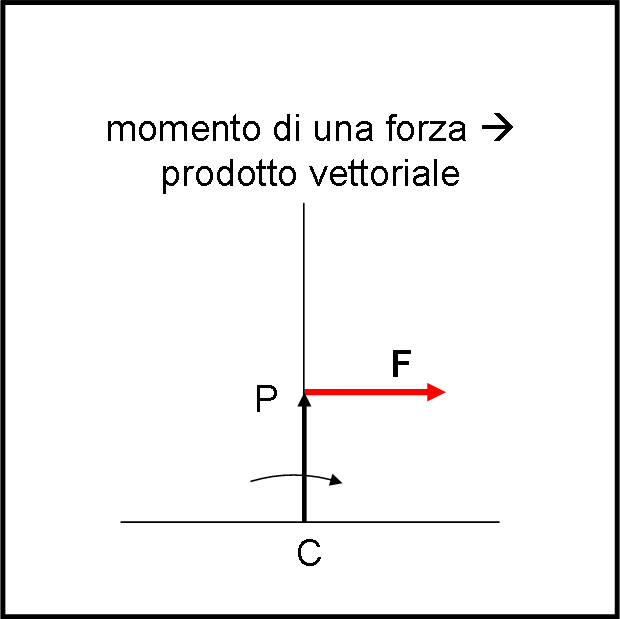
Abbiamo il vettore che identifica il punto di applicazione della forza F (ossia P) rispetto a C. Esso è dato da CP. Abbiamo, poi, la forza F applicata in P. La direzione della forza è proprio perpendicolare al vettore CP e quindi  si ottiene una  rotazione di CP attorno a C (vedi Fig. 25 dell’approfondimento sul momento angolare). Stiamo parlando del momento di una forza che equivale al prodotto vettoriale tra i vettori prima definiti. Il momento è diretto verso di noi o in senso opposto a seconda della direzione di F (regola della mano destra o vite che si svita o s’avvita).

Ne consegue che il rocchetto si muove da una parte o dall’altra solo in base al momento della forza F rispetto al punto di rotazione istantanea C.

La Figura 4 mostra un caso di movimento verso destra per una direzione della forza non perpendicolare al vettore CP.

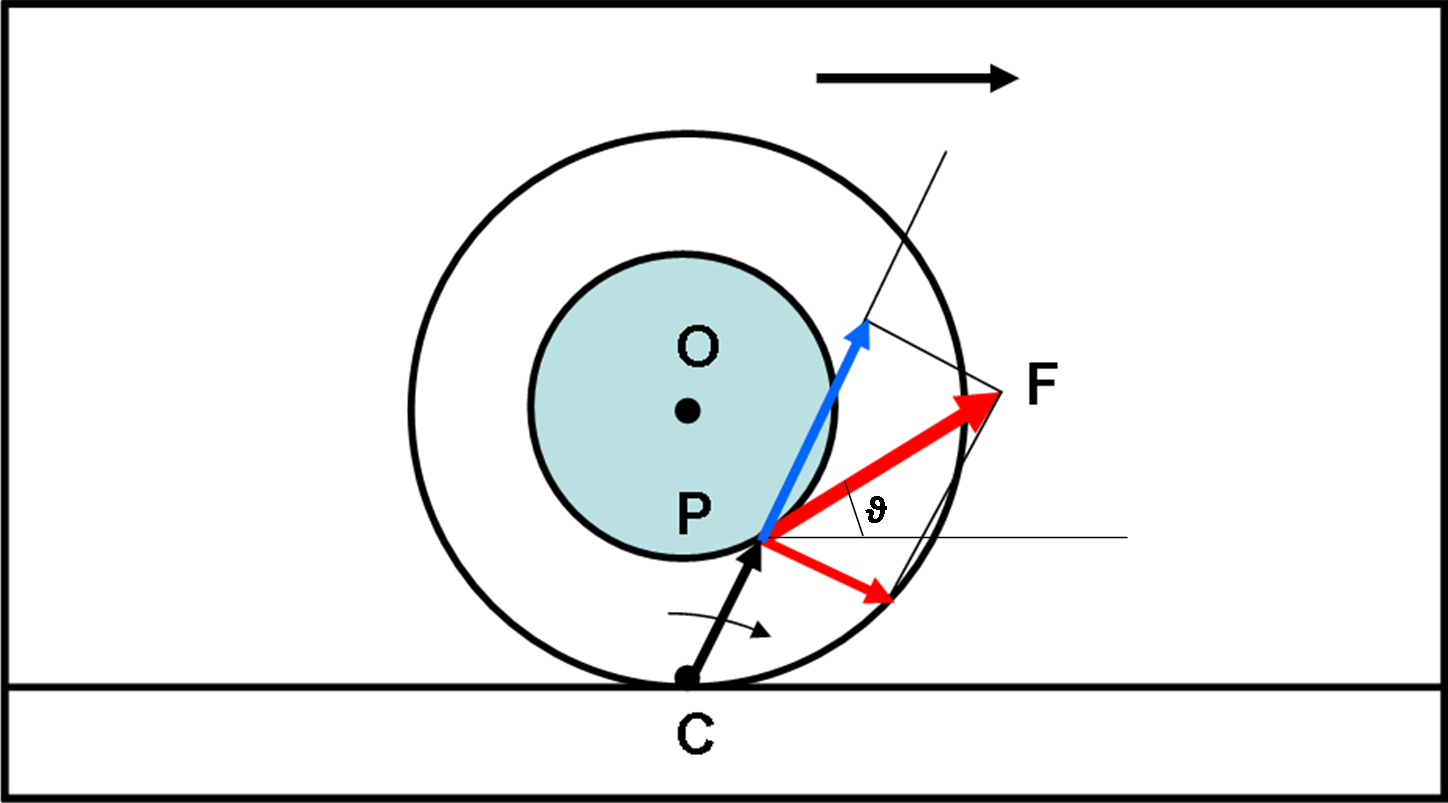
Come imparato nell’approfondimento, si può sempre scomporre il vettore forza F in due componenti molto utili. Una è quella diretta proprio lungo la congiungente CP e l’altra è quella normale a CP. La prima componente non causa rotazione (il prodotto vettoriale è ZERO). Quella che conta è solo la componente normale che è diretta verso destra.

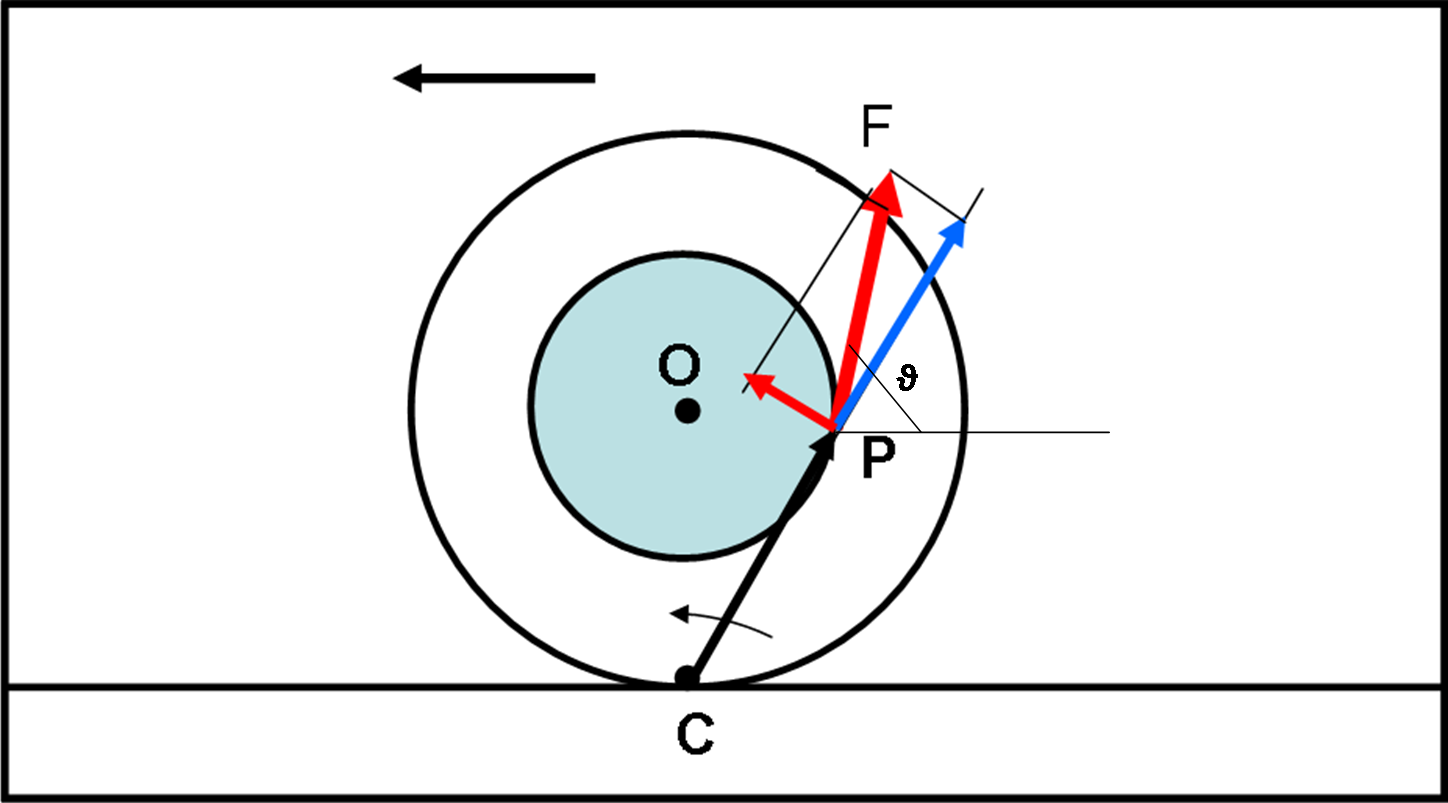
Cosa analoga capita nella Fig. 5, ma questa volta la componente normale “attiva” è diretta verso sinistra: la rotazione avviene in verso antiorario e lo spostamento del rocchetto è verso sinistra.

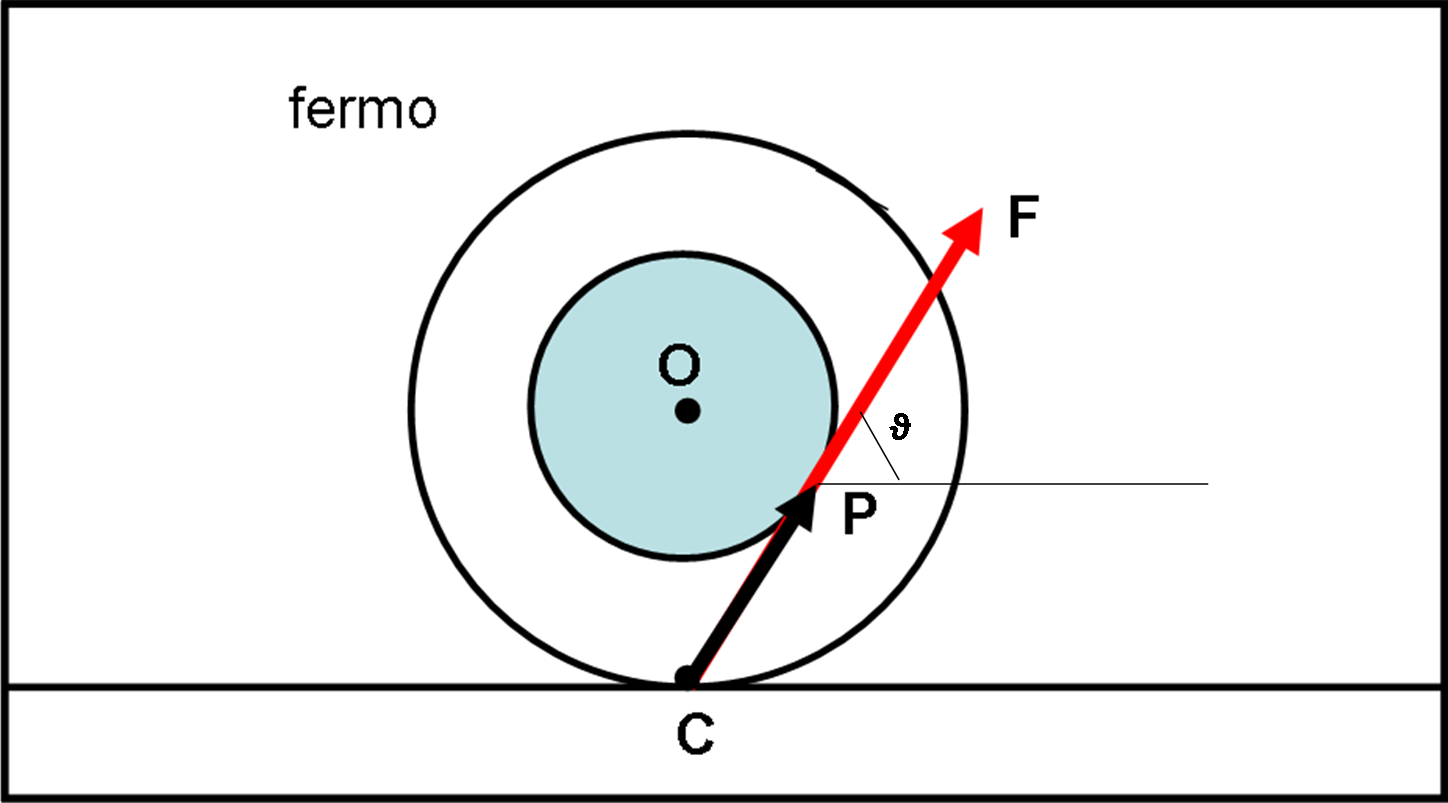
La conclusione, senza bisogno di introdurre formule (facilissime), è che il rocchetto si muove nella direzione indicata dal momento della componente normale alla forza. Va verso destra o verso sinistra a seconda dell’angolo formato dalla forza F e dalla congiungente CP. In particolare, la direzione che fa da confine ai due casi è quella che corrisponde alla forza diretta proprio nella direzione CP (Fig. 6). In questo caso il momento della forza (il prodotto vettoriale) è uguale a ZERO e il rocchetto non può rotolare e quindi spostarsi (ricordiamo che non può SCIVOLARE sul piano d’appoggio).

 

QUI il quiz pubblicato il 24/8/2016 seguito dai commenti

 

Carta igienica e yo-yo

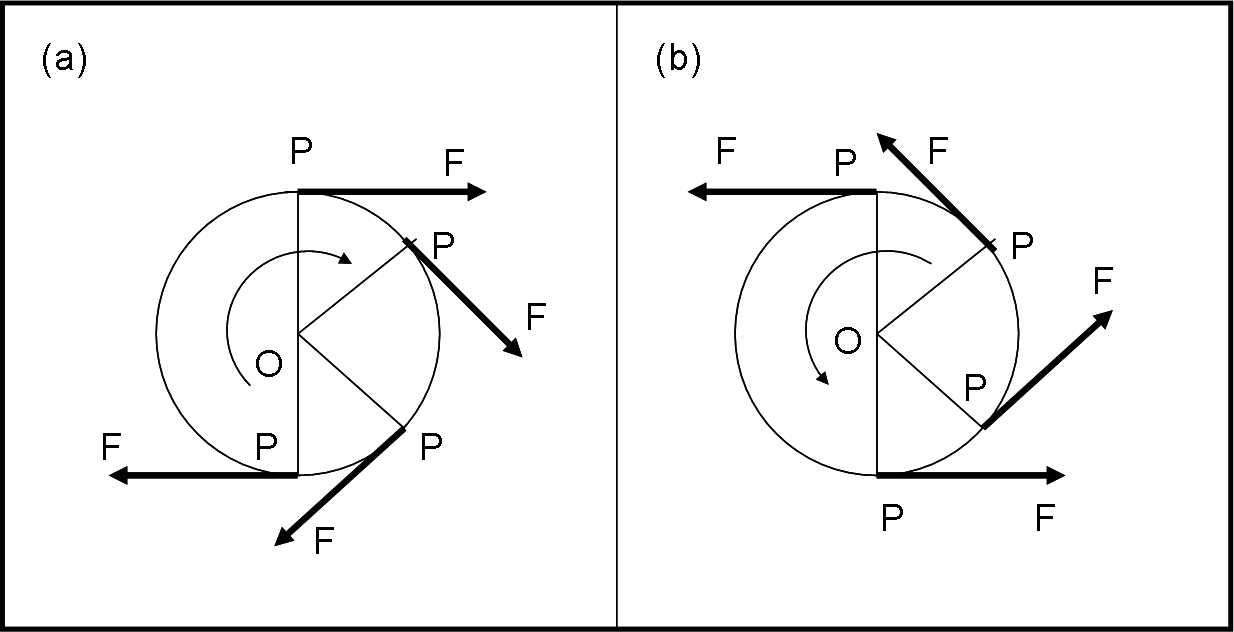
Il caso del rotolo dei carta igienica è decisamente diverso e semplificato. Il rotolo è fissato nel centro O, per cui è il verso della forza F, e il suo momento rispetto a O, a decidere la rotazione, come si vede bene nelle figure 7a e 7b.

Nello YO-YO si ha una ulteriore complicazione, dato che il centro O può spostarsi e le forze che agiscono sono due: quella di gravità e quella impartita dalla mano. Un problemino alquanto intricato e non banale, vediamo come è stato affrontato un caso molto simile (con tanto di verifica sperimentale eseguita dal nostro Arturo Lorenzo, l'uomo del "palloncino"!).

E' POSSIBILE FAR CADERE UN OGGETTO PIU' LENTAMENTE?

Consideriamo un cilindro la cui altezza è molto minore del suo raggio, in pratica un disco con un suo spessore e una sua massa, appeso per uno dei punti della sua circonferenza di bordo ad un filo inestensibile, molto sottile e di massa trascurabile. Il filo, all'altra estremità, è ancorato ad un punto fermo. Inizialmente tutto è in quiete. Consideriamo trascurabile la resistenza dell'aria e qualsiasi altro attrito. Se prendiamo il disco con una mano, lo solleviamo in alto fino al punto dove è ancorato il filo e lo lasciamo cadere liberamente in verticale, esso cade, come tutti sappiamo, con una accelerazione pari a quella di gravità g (=9,81 m/s² circa). Supponiamo che il filo sia appena più lungo dell'altezza dalla quale lasciamo cadere l'oggetto, in modo tale che esso non possa trattenerlo nel momento dell'impatto al suolo.

Ci chiediamo: è possibile far cadere l'oggetto più lentamente, quindi con una accelerazione minore di g, sempre in verticale, senza usare alcuna altra forza se non quella di gravità, e senza spostarci sulla Luna... ? L'esperienza è agevolmente replicabile da chiunque. Quindi saranno gradite, oltre alle risposte, eventuali foto dei propri tentativi.

A questo punto potete decidere se dare la vostra risposta nei commenti oppure continuare a leggere.

 

La risposta alla domanda è affermativa. L'occorrente per far cadere più lentamente il disco cilindrico è già tutto presente e non ci serve altro. Basta solo avvolgere il filo attorno alla superficie laterale del disco cilindrico , portando poi quest'ultimo all'altezza del punto di ancoraggio del filo e lasciandolo cadere in maniera tale che il filo si svolga man mano che il disco cade. Insomma, qualcosa di molto simile ad un gioco con cui molti di noi si saranno almeno una volta divertiti da ragazzi (e anche da grandi): lo yo-yo.

Si osserva in tal modo che il disco cade verticalmente in modo più lento rispetto a quando il filo non è avvolto su di esso. In quel caso, infatti, il disco in caduta semplicemente trasla in direzione verticale, senza ruotare su sè stesso.

Possiamo affrontare analiticamente il problema applicando il principio di conservazione dell'energia meccanica. Abbiamo supposto trascurabili gli attriti e la resistenza del mezzo. Le uniche energie in gioco sono dunque quella cinetica traslazionale , dovuta al fatto che il disco, ad un certo istante t, ha una velocità v(t) diretta verso il basso, l'energia cinetica rotazionale, dovuta al fatto che il disco, all'istante t, ruota , mentre cade, con velocità angolare (t) , e l'energia potenziale gravitazionale, dovuta al fatto che il cilindro , all'istante t, si trova ad una altezza h(t) rispetto al suolo (che assumiamo come piano di riferimento).

Per il principio di conservazione dell'energia deve, dunque, risultare:

               (1)

cioè l'energia meccanica all'istante iniziale deve essere uguale all'energia meccanica al generico istante di tempo t. All'istante iniziale, quando il disco è ancora fermo a quota H dal suolo, abbiamo solo energia potenziale gravitazionale, quindi:

avendo indicato con m la massa del disco cilindrico (quella del filo l'abbiamo supposta trascurabile). All'istante di tempo generico t, invece, il disco è in caduta , quindi ha una velocità di traslazione verso il basso v(t) e una di rotazione attorno al suo asse (t). In particolare, indichiamo con t l'istante di tempo in cui il disco impatta al suolo. In tale istante l'energia potenziale gravitazionale iniziale si sarà completamente convertita in energia cinetica traslazionale e rotazionale. Quindi, nell'istante di impatto, l'energia meccanica sarà data solo da energia cinetica:

avendo indicato con I il momento di inerzia del disco rotante attorno al proprio asse (pari a  , se con R indichiamo il raggio del disco)

Per la (1), dunque , risulta:

           (2)

Inoltre, il filo avvolto al disco, mentre si svolge, non slitta sulla superficie laterale del disco (perché lo avevamo precedentemente ben fissato ad una estremità al disco e lo avevamo ben avvolto attorno ad esso). Vi è dunque una perfetta corrispondenza tra la velocità di traslazione verso il basso del disco e quella di rotazione attorno al suo asse. Si ha, cioè, che:

che , sostituita nella (2) permette di riscriverla come:

cioè, sostituendo ad I la sua espressione:

cioè:

da cui, dividendo tutto per m ed esplicitando rispetto a v:

Se confrontiamo tale espressione con quella nota della velocità   con cui un oggetto in caduta libera da altezza H impatta al suolo , pari a , ci accorgiamo che

        (perché )

In definitiva, il disco che cade avvolto sul filo a cui era sospeso, lo fa più lentamente rispetto alla caduta libera senza alcun filo.

Volendo sapere con quale accelerazione avviene la caduta del disco, basta applicare le leggi orarie del moto uniformemente accelerato, dove, al posto di g ci mettiamo a, incognita del problema.

In particolare , usiamo la legge:

avendo indicato con s lo spazio percorso.

Essendo, nel nostro caso, H lo spazio totale percorso durante il moto uniformemente accelerato con accelerazione a , ed essendo nulla la velocità iniziale v(0) , alla fine otteniamo:

da cui, esplicitando rispetto ad a:

sostituendo ora a v l'espressione prima ottenuta, si ha:

In definitiva, l'accelerazione con cui il disco con il filo avvolto cade verticalmente è pari a 2/3 di quella di gravità.

Ma vediamo un caso pratico. Analizziamolo dapprima in maniera simulata, utilizzando cioè il computer. Abbiamo due dischi identici, stessa massa, stesso diametro, stesso materiale, posti alla stessa altezza H dal suolo (nel modello pari a 12 metri). Al disco di sinistra è avvolto senza lasco il filo inestensibile e di massa trascurabile. Il disco di destra è assolutamente libero. Li lasciamo cadere nello stesso istante. Il video seguente illustra la caduta simulata con il computer:

OK, il filo attorno al disco di sinistra non è avvolto esattamente come nel quiz, ma non si poteva fare di meglio nella fase di modellazione. I grafici sulla destra sono quelli della velocità dei dischi in funzione del tempo. Il grafico superiore è relativo al disco di destra, ossia quello in caduta libera senza filo. Quello inferiore è relativo al disco di sinistra, ossia quello con il filo avvolto.

Naturalmente, la pendenza media dei due grafici non è altro che la derivata della velocità rispetto al tempo, cioè l'accelerazione.

Ingrandiamo tali grafici.

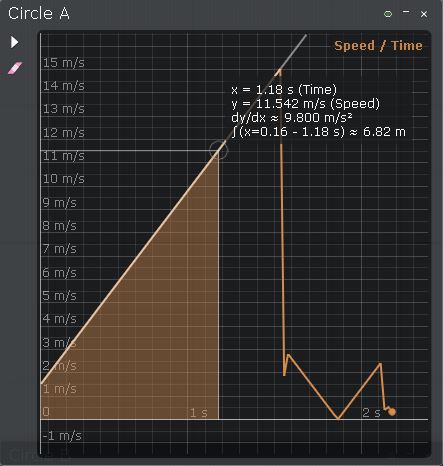
La velocità con cui il disco di destra impatta al suolo è di circa 15 m/s, in ottimo accordo con la teoria. L'accelerazione in questo caso è quella di gravità.

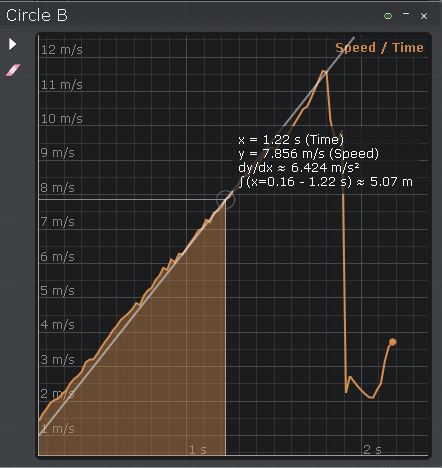
Nel caso del disco con il filo avvolto, invece, la velocità con cui esso impatta al suolo risulta di circa 11,5 m/s, leggermente inferiore a quella attesa in base alla teroia (12,5 m/s), sicuramente per le approssimazioni del modello a proposito del filo avvolto sul disco. L'accelerazione media risulta pari a circa 6,4   , in buon accordo con il valore atteso in base alla teoria (6,54 ).

Ora vi proponiamo, un caso pratico nel vero senso del termine.. 

Due pulegge in alluminio assolutamente identiche, ma una con il solito filo di massa trascurabile e ben avvolto attorno, vengono fatte cadere contemporaneamente da una stessa altezza (circa 2,30 metri) e riprese con una Go-Pro Hero2 impostata a 100 frames/s. Abbiamo rallentato il video così da ottenere un effetto "slow motion". La qualità del risultato non è il massimo, ma crediamo sia sufficiente per i nostri fini.

E' evidente la caduta più lenta del disco a sinistra, quello con il filo avvolto. Il materassino gonfiabile in basso è servito a evitare che l'energia cinetica delle pulegge in caduta si trasferisse nell'urto al pavimento sottostante, con conseguenze imprevedibili sulla tenuta familiare... 

QUI il quiz pubblicato il 25/3/2017 seguito dai commenti

 

Se vi è piaciuto questo NON-QUIZ, ne trovate altri QUI