Questo quiz-non quiz fa parte della serie "Minkowski per tutti". Le soluzioni sono inserite in questo stesso articolo, ma sarebbe più interessante provare, prima di leggerle, a darle nei commenti, anche solo per esprimere le eventuali difficoltà incontrate.
Questo articolo era già apparso, ma il compito dei tre giudici non era stato definito molto bene e ne conseguivano soluzioni ambigue. Ringrazio Guido per avere sollevato il problema. In questa versione credo che i vari compiti siano decisamente ben stabiliti... comunque, se vi sono problemi... parliamone! Con Achille e la tartaruga non si sa mai dove si va a finire...
Ci ricordiamo bene il paradosso di Zenone relativo alla sfida tra Achille e la tartaruga. In quel caso si era di fronte a una battaglia tra matematica e fisica. Adesso, inserendo la relatività speciale e la velocità della luce, le cose si complicano ancora di più.
Ricordiamoci di tenere bene a mente che siamo interessati sia all'ordine cronologico di ciò che accade nei vari sistemi di riferimento sia a cosa vedono realmente Achille, la tartaruga e i giudici a seconda dei loro compiti effettivi . Un sistema di riferimento ha tutti i suoi orologi sincronizzati perfettamente. In altre parole, possiamo immaginare che un orologio del sistema di Achille sia sempre accanto alla tartaruga e viceversa. Per i giudici capita la stessa cosa. Ben diversa è la situazione quando siamo interessati a ciò che vedono realmente Achille e la tartaruga. Non dimentichiamolo mai...
La sfida tra Achille e la tartaruga non finisce mai e assume risvolti sempre più ambigui. In questo caso, vi sono ben tre giudici che dovrebbero dare una valutazione imparziale anche se sappiamo che sia la tartaruga che Achille sono atleti che non mentono mai e che accettano la realtà dei fatti, qualunque essa sia. Lungi da loro cercare di barare!
Tutto dovrebbe, perciò, svolgersi in modo perfetto e, invece, non si riesce mai a trovare un accordo... E pensare che la gara viene svolta in tre modi diversi.
La tartaruga, dimenticando la furbizia di Zenone, ammette di non potere fronteggiare le poderose leve di Achille e accetta la gara solo se viene favorita da un percorso uguale solo alla metà di quello di Achille. In altre parole, il traguardo della tartaruga dista dalla partenza la metà di quello di Achille. Achille non si preoccupa assolutamente e accetta senza alcun tentennamento, essendo sicuro di sé.
a)Fianco a fianco
La prima gara vede gli atleti partire insieme e correre nella stessa direzione verso i due traguardi, con quello della tartaruga posto a metà strada rispetto a quello di Achille. Vi è un giudice di partenza e un giudice per ogni traguardo. Lo schema è quello di Fig. 1, dove A è Achille, T la tartaruga, GP il giudice di partenza e GA e GT i giudici addetti ai traguardi di Achille e della tartaruga (e, quindi, indicano anche la posizione dei due traguardi).
Figura 1
Gli atleti partono insieme e si fermano immediatamente nel momento del loro arrivo.
Teniamo ben presente che i giudici GT e GA fanno partire i loro orologi sincronizzati con quello del giudice di partenza GP. Non hanno bisogno di veder partire gli atleti: quello è un compito che spetta al giudice di partenza GP. I giudici di arrivo devono solo schiacciare il cronometro quando i due atleti arrivano fisicamente vicini a loro.
1a.I due giudici di arrivo danno una perfetta parità, che è confermata anche dal giudice di partenza. Chi vince, invece, nei sistemi di Achille e della tartaruga? Disegnare il diagramma relativo.
I giudici e i due atleti sono molto imbarazzati e decidono di basarsi solo su ciò che vedono direttamente.
2a.Cosa concludono giudici e atleti? Disegnare il diagramma relativo.
Come si può notare le cose sono cambiate non di poco...
b) Occhio che non vede, cuore che non sente
La tartaruga non è del tutto contenta di se stessa ed è convinta che aver visto Achille superarla subito le abbia causato una crisi psicologica che ha limitato le sue potenzialità atletiche. Propone, allora, di rifare la gara, ma mettendo i due traguardi (sempre alla stessa distanza di prima rispetto alla linea di partenza) in direzioni opposte, In tal modo, la tartaruga correrà nel verso opposto di Achille e non lo vedrà scappar via. Lo schema è quello di Fig. 2.
Figura 2
I giudici concludono nuovamente che nel loro sistema la gara è finita in parità, ma in quello della tartaruga e di Achille le cose sono cambiate. L'accordo è ancora lontano...
1b. Cosa concludono Achille e la Tartaruga? Ovviamente, il diagramma relativo è obbligatorio...
Come già fatto prima, si ripiega sulla visione diretta, ma non si ottiene niente di meglio...
2b. Cosa concludono giudici e atleti? Senza dimenticare il diagramma relativo...
c) Partenza separata
Non resta che fare un terzo tentativo. Questa volta i due atleti partono separatamente, in modo tale che il traguardo comune mantenga le distanze relative ai due atleti, come mostra la Fig. 3 . Questa volta il giudice GP è in realtà un giudice di arrivo... Gli altri due si occupano, adesso, della partenza dei due atleti.
Figura 3
1c. Cosa succede nei rispettivi sistemi di riferimento e nella visione diretta? Diagramma compreso, come sempre...
Mamma mia... sembra un miracolo! Ma è di breve durata... purtroppo. E' bastato, infatti, controllare le partenze e tutto è tornato nel caos, sia considerando i sistemi di riferimento sia passando alla visione diretta.
2c. Cosa succede nei rispettivi sistemi di riferimento e nella visione diretta, analizzando la partenza? Il diagramma è più che obbligatorio!
Amici miei, tra relatività speciale e velocità della luce forse era meglio farsi imbrogliare matematicamente da Zenone...
RISPOSTA
Chi vuole conoscere subito la risposta, non deve fare altro che schiacciare "mostra risposta" (invitiamo, però, chi conosce le basi della RR a provare, prima, da solo...)
Disegniamo subito il diagramma di Minkowski che ci permette di riassumere i fatti accaduti nella prima gara e le conclusioni a cui sono giunti i nostri cinque personaggi (i tre giudici e i due atleti), nei due metodi di valutazione proposti.
In Fig. 4a vediamo la descrizione della gara, dove la linea rossa si riferisce al moto di Achille e quella blu al moto della tartaruga. Ovviamente Achille corre più forte e "sembrano" giungere contemporaneamente ai loro traguardi indicati con RA e RT. Nel sistema dei giudici (quello in quiete, in nero) l'arrivo è ovviamente simultaneo ed essi non possono che concludere con un verdetto di parità. I due concorrenti, però, non sono assolutamente d'accordo (Fig. 4b).
Figura 4
La tartaruga si muove lungo la linea azzurra e quando giunge in T2 deve ammettere che l'evento A (arrivo di Achille sul traguardo) sta avvenendo proprio in quel momento (T2 e A sono eventi simultanei nel suo sistema di riferimento). Deve accettare la sconfitta. D'altra parte essa è confermata anche dal più che corretto Achille: quando lui giunge in A, nel suo sistema di riferimento rosso, la tartaruga è ancora in T1, ben lontana dal suo traguardo (T1 e A sono eventi simultanei nel suo sistema).
La parità valutata dai tre arbitri si scontra nettamente con quanto hanno verificato direttamente Achille e la tartaruga. Addirittura, la tartaruga ha confermato senza esitazione di avere perso. Riassumendo, questa è la conclusione secondo i cinque personaggi (la seconda colonna indica il vincitore):
giudice RP : parità
giudice RA : parità
giudice RT : parità
Achille: Achille
tartaruga: Achille
La situazione è molto scomoda e imbarazzante. Forse è meglio lasciar perdere i sistemi di riferimento e la loro simultaneità e fidarsi solo di quello che viene visto dai cinque personaggi.
Disegniamo, allora, la Fig. 5, dove entra in gioco la luce e la sua velocità (linee arancioni).
Figura 5
Ricordiamo, anche, che i due atleti si fermano appena arrivati e quindi entrano a far parte del sistema in quiete. Cosa dicono i giudici RA e RT? Loro non possono che confermare la parità, dato che sia la partenza che l'arrivo non vengono minimamente modificati dalla velocità della luce. La partenza è data dal giudice di partenza RP e loro non fanno altro che far partire il cronometro all'ora stabilita, in precedenza: non hanno alcun bisogno di vedere veramente gli atleti fino a quando non arriveranno dove sono loro. I loro orologi sono sempre sincronizzati appartenendo allo stesso sistemi di riferimento. per RT e RA
Per RT e RA continua a esserci parità (i loro orologi segnano lo stesso tempo). La tartaruga, invece, una volta arrivata, deve ancora aspettare un bel po' di tempo per VEDERE arrivare Achille, ossia solo quando è nella posizione TA. Per la tartaruga è lei la vincitrice! Achille, invece, è sicurissimo di essere arrivato per primo. Deve infatti aspettare di arrivare in AT per vedere arrivare la tartaruga.
Forse conviene sentire il giudizio del giudice di partenza RP. Lui ha visto realmente partire insieme i due atleti e ha fatto scattare il suo cronometro all'ora stabilita con i suoi colleghi. Tuttavia, lo stesso suo cronometro è costretto a dare tempi di arrivo diversi per la tartaruga e per Achille. Per lui ha vinto la tartaruga che vede in RTA, L'immagine dell'arrivo di Achille gli arriva più tardi (RAC). Non può che dare la vittoria alla tartaruga.
In conclusione:
giudice RP : tartaruga
giudice RA : parità
giudice RT : parità
Achille: Achille
tartaruga: tartaruga
Un risultato che non accontenta nessuno... e' molto meglio cambiare strategia di gara, anche perché la tartaruga è convinta di poter fare ancora meglio.
Risposte 1b e 2b
La Fig. 6 riporta la situazione, lavorando nuovamente sui sistemi di riferimento.
Figura 6
In Fig. 6a si vede chiaramente che anche in questo caso i tre giudici sono concordi e danno la parità. La tartaruga e Achille (Fig. 6b) non sono, invece, d'accordo come nella gara precedente (trattando con i sistemi). La tartaruga, quando taglia il traguardo, si accorge che nel suo sistema questo evento è simultaneo con A1. Il che vuol dire che Achille deve ancora farne di strada... Purtroppo, alla stessa conclusione giunge anche Achille appena supera il traguardo: In quel momento, nel suo sistema di riferimento, la tartaruga si trova ancora in T1. Lui ha sicuramente stravinto.
Una conclusione ancora diversa che si riassume come segue:
giudice RP : parità
giudice RA : parità
giudice RT : parità
Achille: Achille
tartaruga: tartaruga
Non resta che affidarsi di nuovo a ciò che stabilisce la visione diretta degli eventi da parte dei cinque personaggi. Costruiamo così la Fig. 7. Per RT e RA la parità è indiscutibile. Per la tartaruga è lei la vincitrice dato che vede arrivare Achille solo quando è in TA, ma per Achille è lui il vincitore: Deve aspettare di vedere l'arrivo della tartaruga solo quando è già arrivato da parecchio tempo, ossia in AT. Ancora una volta lasciano la decisione al giudice RP. Lui, purtroppo, deve ancora una volta contraddire il risultato dei suoi colleghi. Fermo restando che il suo cronometro è partito all'ora esatta, è adesso costretto a fermarlo prima per l'arrivo della tartaruga (quando è in RTA) e solo dopo per l'arrivo di Achille (quando è in RAC).
Figura 7
Si ha una nuova conclusione:
giudice RP : tartaruga
giudice RA : parità
giudice RT : parità
Achille: Achille
tartaruga: tartaruga
Ancora una volta, la luce sembra dare ragione alla tartaruga. Tuttavia, non si può concludere una gara con risultati così altalenanti.
Risposte 3a e 3c
La figura da considerare è la Fig. 8.
Figura 8
Fantastico! sembra impossibile, ma questa volta il risultato sembra decisamente lo stesso per tutti e cinque: parità assoluta nel caso dei sistemi di riferimento.
giudice RP : parità
giudice RA : parità
giudice RT : parità
Achille: parità
tartaruga: partita
Per non lasciare niente di intentato, decidono comunque di affidarsi anche a ciò che vedono i 5 personaggi. Nessun problema per Achille, la tartaruga e il giudice di arrivo RP. L'evento F che è l'arrivo simultaneo di Achille e della tartaruga nei tre sistemi di riferimento, viene visto direttamente proprio come F sia dai due atleti che dal giudice RP (diventato giudice di arrivo).
Si sente, però, un po' di malcontento negli altri due giudici. Loro sono pienamente d'accordo sull'arrivo simultaneo, ma non sul tempo impiegato a terminare la gara chiusa in parità, Non dovrebbero nemmeno occuparsene, ma l'arrivo simultaneo dei due atleti viene visto come AF e TF , in tempi diversi . Per RT la gara è durata di meno che per RA. Sono costretti a dare parità, anche se con un dubbio sul tempo di durata della gara...
giudice RP : parità
giudice RA : parità ?
giudice RT : parità ?
Achille: parità
tartaruga: partita
Possiamo chiudere la faccenda? Sembrerebbe di sì, ma quanto commentato dai due giudici RA e RT fa sorgere dei dubbi sia alla tartaruga che ad Achille e il problema diventa ancora più imbarazzante di quelli precedenti (Fig. 9).
Figura 9
Achille e la tartaruga contestano il fatto che la partenza sia stata veramente simultanea nei loro sistemi di riferimento! In particolare, la tartaruga dice che la sua partenza si è effettuata quando Achille si trovava già in A1. Nel suo sistema di riferimento, A1 è simultaneo con la sua partenza, il che vuol dire che Achille è partito prima. Un inganno? No non può crederci...
Achille, però, dice la stessa cosa: lui stava partendo, ma nel suo sistema la tartaruga era già in T1. Anche lui non può credere a un inganno. Tuttavia, i giudici confermano che la partenza è stata simultanea nel loro sistema. La conclusione sulla partenza sembrerebbe questa:
giudice RP : parità
giudice RA : parità
giudice RT : parità
Achille: tartaruga
tartaruga: Achille
i nomi della seconda colonna si riferiscono a chi, per ogni personaggio, sarebbe partito per primo.
Non resta che considerare ciò che ognuno vede direttamente. I giudici RT e RA non possono che confermare di avere dato il via al momento stabilito (ipotesi di partenza di ogni gara). Achille e la tartaruga sembrano, invece, completamente disorientati (Fig. 10). Devono cambiare totalmente le loro conclusioni...
Figura 10
La tartaruga deve ammettere di vedere la partenza di Achille quando lei si trova già in TA. Accidenti, ma allora è lei che è partita per prima... Achille, però, non è meno sbalordito. Anche lui si accorge che vede partire la tartaruga quando è già in AT. Accidenti, è lui che è partito per primo!
Non resta che chiedere a RP. In realtà, lui dovrebbe solo misurare il tempo di arrivo, sicuro di aver fatto partire il suo orologio alla stessa ora dei suoi colleghi. Gli si rizzano i capelli in testa! Si accorge che le partenze non sono state simultanee tra loro e diverse dal tempo stabilito a priori...
Infatti, RP vede partire prima la tartaruga (in RTA) e dopo un po' di tempo Achille (in RAC)
Riassumendo si ha una conclusione veramente caotica:
giudice RP : tartaruga
giudice RA : parità
giudice RT : parità
Achille: Achille
tartaruga: tartaruga
La gara termina nel caos più completo! I due giudici RA e RT sono sicuri di aver dato la partenza in modo simultaneo (d'altra parte è l'ipotesi di partenza!). Il giudice RP è anche lui convinto dell'onestà dei suoi collaboratori, ma ciò che vede sembra ben diverso. Qualcuno ha sicuramente barato! Nel frattempo, Achille e la tartaruga si scusano l'uno con l'altro e alla fine non possono che prendersela con i giudici.
P.S. se ammettessimo che i giudici RA e RT non siano stati onesti si dovrebbe cambiare il tutto, ma la faccenda è già abbastanza complicata.
Sì, è proprio vero... molto meglio affidarsi a Zenone!
Al momento posso lavorarci solo in modo discontinuo e poiché mi rendo conto di essere lento nell’elaborazione delle figure avrei deciso di postare la mia soluzione divisa in 3 parti via via che completo le figure. In tal modo chi volesse potrebbe anche trarre spunto dalla mia impostazione (che spero corretta) per proseguire mentre porto avanti il resto. Non mi riferisco a Paolo che sappiamo bene essere un esperto di Minkowski e di RR e che di certo ha già risolto il tutto.
PARTE 1 – fianco a fianco
Parto dalla considerazione che l’evento “arrivo al traguardo della tartaruga e di Achille” è simultaneo nel sistema di riferimento dei giudici (sistema in quiete). Quindi riporto sul classico grafico di Minkowski X-t (in nero) i punti che corrispondono all’arrivo della tartaruga e di Achille (istante t). Essi saranno posizionati all’istante Tarr sulle rispettive linee d’universo dei giudici GP, GT e GA (in verde), con la distanza tra GT e GA uguale alla distanza GP-GT come suggerisce lo schema del testo. Aggiungo nella figura che segue anche la linea della velocità della luce (in giallo) e inclinata di 45° come vuole Minkowski, che servirà dopo.
Sia la tartaruga che Achille rappresentano invece sistemi in moto (uniforme) e pertanto occorre riportare gli assi X-t dei loro rispettivi sistemi di riferimento. La tartaruga è più lenta e quindi la “forbice” tra gli assi del suo sist. di riferimento è più aperta (assi viola) che nel caso di Achille (assi rossi). Vedi fig.1.
fig1
Trasporto ora il punto viola, cioè l’evento “arrivo della tartaruga” nel sistema di riferimento di Achille, tracciando la parallela all’asse XA (linea rossa tratteggiata) ed ottenendo il punto viola sull’asse dei tempi “achillei”. Poi riporto il punto rosso, cioè l’evento “arrivo di Achille” nel sist. di rif. della tartaruga tracciando la parallela all’asse XT (linea tratteggiata viola) ed ottenendo il punto rosso sull’asse dei tempi “tartarugheschi”. Vedi fig. 2.
fig.2
Quindi si vede che nel sist. di Achille vince Achille (la tartaruga arriva dopo) e nel sist. di rif. della tartaruga anche (Achille arriva prima), come indicano le rispettive posizioni dei punti rosso e viola.
Per capire cosa vedono giudici ed atleti occorre considerare i percorsi della luce rispetto a chi percepisce le immagini. Giudice GP: traccio le perpendicolari alla linea gialla dai pti che rappresentano l’arrivo della tartaruga e di Achille ed ottengo i pti 1 e 2, il giudice GP vede arrivare prima la tartaruga e poi Achille.
Giudice GT: l’intersezione con la perpendicolare alla linea gialla dal pto che rappresenta l’arrivo di Achille fornisce la posizione del pto 3 mentre l’arrivo della tartaruga su questa linea d’universo è il pto viola, il giudice GT vede arrivare prima la tartaruga e poi Achille.
Giudice GA: l’intersezione con la parallela alla linea gialla dal pto che rappresenta l’arrivo della tartaruga fornisce la posizione del pto 4 mentre l’arrivo di Achille su questa linea d’universo è il pto rosso, il giudice GA vede arrivare prima Achille e poi la tartaruga. La stessa linea prolungata fino all’asse del tempo achilleo (tA) fornisce il pto 5, e quindi Achille vede la tartaruga tagliare il traguardo dopo di lui.
L’intersezione tra la perpendicolare alla linea gialla condotta dal pto che rappresenta l’arrivo di Achille e l’asse del tempo tartarughesco (tT) fornisce il pto 6, e quindi la tartaruga vede Achille tagliare il traguardo dopo di lei. vedi fig.3.
Rispetto al caso precedente occorre spostare GT con la sua linea d’universo a sin di GP, mantenendo invariata la distanza da GP stesso, come dice lo schema del testo. Gli assi del sistema tartarughesco ora devono essere ribaltati rispetto agli assi del sistema in quiete (in nero) poiché la tartaruga si sposta nel verso contrario a quello di Achille.
Con la medesima procedura utilizzata in fig. 2 si ottengono ora il pto viola sull’asse rosso e pto rosso sull’asse viola che rappresentano, rispettivamente, gli eventi “arrivo della tartaruga” rispetto al sistema achilleo e “arrivo di Achille” rispetto al sistema tartarughesco. Vedi fig. 4
Quindi si vede che nel sist. di Achille vince Achille (la tartaruga arriva molto dopo) mentre nel sist. di rif. della tartaruga vince la tartaruga (Achille arriva dopo), come indicano le rispettive posizioni dei punti rosso e viola.
Per capire cosa vedono giudici ed atleti considero i percorsi della luce rispetto a chi percepisce le immagini, come prima.
Giudice GP: traccio la perpendicolare alla linea gialla dal pto che rappresenta il momento in cui egli vede arrivare Achille ed ottengo il pto 2, l’intersezione con la parallela alla linea gialla è il pto 1 che rappresenta il momento in cui egli vede arrivare la tartaruga, quindi il giudice GP vede arrivare prima la tartaruga e poi Achille.
Giudice GT: con le medesime rette si ottiene l’intersezione 3 che rappresenta il momento in cui il giudice vede arrivare Achille mentre l’arrivo della tartaruga su questa linea d’universo è il pto viola, il giudice GT vede arrivare prima la tartaruga e poi Achille.
Giudice GA: l’intersezione con la parallela alla linea gialla dal pto che rappresenta l’arrivo della tartaruga fornisce la posizione del pto 4 mentre l’arrivo di Achille su questa linea d’universo è il pto rosso, il giudice GA vede arrivare prima Achille e poi la tartaruga. La stessa linea prolungata fino all’asse del tempo achilleo (tA) fornisce il pto 5 (mi finisce fuori grafico ma se mi rimetto a disegnare tutto si fa notte…), e quindi Achille vede la tartaruga tagliare il traguardo ben dopo di lui.
L’intersezione tra la perpendicolare alla linea gialla condotta dal pto che rappresenta l’arrivo di Achille e l’asse del tempo tartarughesco (tT) fornisce il pto 6, e quindi la tartaruga vede Achille tagliare il traguardo dopo di lei. vedi fig. 5.
Quando hai finito, fai uno schemino che indichi cosa dicono i tre giudici e Achille e la Tartaruga in ogni singolo caso. Così sarà più facile controllare il risultato...
Ecco la terza ed ultima parte. In fondo riassumo tutti i miei risultati.
PARTE 3
Rispetto al caso iniziale riposiziono l’origine dei rispettivi assi di riferimento concordemente con le partenze separate in GT e GA . Achille inoltre si muove verso sin mentre la tartaruga verso ds, quindi ruoto gli assi del sistema di riferimento di Achille in senso opposto. Si vede che i 2 concorrenti arrivano in perfetta contemporaneità sull’asse t del sistema in quiete (pallino nero) nonché del giudice GF. Anche per i due sistemi di riferimento dei concorrenti tutto torna, c’è contemporaneità e quindi i pallini viola e rosso si sovrappongono a quello nero. L’osservazione diretta conferma tutto, infatti anche sulle linee d’universo dei giudici GT e GA i pallini, proiettati al solito modo secondo la linea gialla della luce, coincidono (punti 1 e 2) tanto per GA che per GT. Vedi fig. 6
Per controllare le partenze occorre riportare il punto GT della partenza della tartaruga nel sistema di riferimento di Achille (assi rossi), ottenendo il pto PT’ (pallino viola) e analogamente riportando il punto GA (partenza di Achille) nel sist. di rif. della tartaruga (assi viola) si ottiene il pto PA’ (pallino rosso).
Per i 3 giudici l’evento della partenza è simultaneo, mentre nel sistema della tartaruga Achille è partito prima. Anche nel sistema di Achille la tartaruga è partita prima.
Il giudice GF vede partire la tartaruga all’istante 3, il giudice GA all’istante 5 e Achille la vede partire all’istante 4.
Il giudice GT vede la partenza di Achille all’istante 8, la tartaruga lo vede partire all’istante 7. Vedi fig. 7
Se ho disegnato e ragionato correttamente dovremmo avere le seguenti riposte:
PARTE 1
Nel sistema di Achille vince Achille
Nel sistema della tartaruga vince sempre Achille
Verifica visiva: il giudice GP vede arrivare prima la tartaruga, il giudice GT vede arrivare prima la tartaruga e il giudice GA vede arrivare prima Achille. La tartaruga vede Achille arrivare dopo di lei, Achille la vede invece arrivare dopo di lui.
PARTE 2
Nel sistema di Achille vince Achille
Nel sistema della tartaruga vince la tartaruga
Verifica visiva: il giudice GP vede arrivare prima la tartaruga, il giudice GT vede arrivare prima la tartaruga e il giudice GA vede arrivare prima Achille. La tartaruga vede Achille arrivare dopo di lei, Achille la vede invece arrivare dopo di lui.
PARTE 3
Nel sistema di Achille, della tartaruga e dei 3 giudici l’arrivo dei 2 concorrenti è simultaneo, la verifica visiva conferma la simultaneità.
Controllo partenze:
Nel sistema di Achille la tartaruga è partita prima di lui.
Nel sistema della tartaruga invece è stato Achille a partire prima di lei.
Verifica visiva: il giudice GF vede partire prima la tartaruga, il giudice GT vede partire prima la tartaruga e il giudice GA vede partire prima Achille. La tartaruga vede Achille partire dopo di lei, Achille la vede invece partire dopo di lui.
avevo valutato male i giudici... comunque controlla adesso la tua risposta con la mia e vediamo se tutto torna... potrei aver fatto anch'io un po' di confusione... adesso dovrebbe essere giusta la risposta...
Caro Enzo, prima di leggere i commenti e la soluzione, vorrei provare a rispondere anch'io alle domande del quiz.
Come al solito per i sistemi di riferimento userò le linee di simultaneità(quando gli orologi sincronizzati di quel sistema segnano lo stesso tempo):
nere e parallele all'asse x per i giudici;
blu e parallele all'asse x' per la Tartaruga;
rosse e parallele all'asse x'' per Achille,
La prima figura risponde alla prima domanda, ossia chi vince nei vari sistemi ?
Per il sistema dei giudici Achille e la Tartaruga arrivano insieme al traguardo al tempo tF (vedi linea di simultaneità nera).
Per il sistema della Tartaruga, quando lei raggiunge il traguardo (t'T) Achille l'ha già raggiunto (tempo t'A, linea di simultaneità blu).
Per il sistema di Achille, la tartaruga raggiunge il traguardo (t''T linea di simultaneità rossa) dopo che lui è già arrivato (t''A ).
Quindi per entrambi vince Achille.
Il disaccordo tra giudici e atleti, dipende ovviamente dal fatto che ogni sistema ha le sue linee di simultaneità!
La seconda figura mostra che cosa vedono direttamente i vari personaggi.
Questa volta, a differenza di prima, la Tartaruga vede Achille raggiungere il traguardo (t'lA) dopo di lei (t'T).
Achille vede la Tartaruga raggiungere il traguardo (t''lT) dopo di lui (t''A).
Due giudici (Gp e GT) vedono arrivare al traguardo prima la Tartaruga e poi Achille, mentre il terzo giudice (GA) vede arrivare prima Achille (tF) e poi la Tartaruga (tlT).
Quindi, basandosi su ciò che si vede: per la Tartaruga ha vinto lei, per Achille ha vinto lui, per due giudici ha vinto la tartaruga e per un terzo giudice ha vinto Achille.
C'è un totale disaccordo, ma d'altronde la visione diretta non tiene conto del tempo impiegato dalla luce per percorrere la distanza che ci separa dall'evento che si osserva.
Nella figura ho anche mostrato la luce che parte dal punto di partenza, che mostra il ritardo con cui raggiunge prima il giudice GT e poi il giudice GA.
La terza figura risponde alla terza domanda, ossia chi vince nei vari sistemi cambiando lo schema di partenza?
Per il sistema dei giudici Achille e la Tartaruga arrivano insieme al traguardo (al tempo tF).
Per il sistema della Tartaruga, Achille raggiunge il traguardo (t'A) dopo che lei è già arrivata (t'T).
Per il sistema di Achille, la tartaruga raggiunge il traguardo (t''T) dopo che lui è già arrivato (t''A).
La quarta figura mostra che cosa vedono direttamente i vari personaggi, nel secondo schema di partenza.
La Tartaruga vede Achille raggiungere il traguardo (t'lA) dopo di lei (t'T) ed Achille vede la Tartaruga raggiungere il traguardo (t''lT) dopo di lui (t''A).
Due giudici (GT e GP) vedono arrivare al traguardo prima la Tartaruga e poi Achille, mentre il terzo giudice (GA) vede arrivare prima Achille (tF) e poi la Tartaruga (tlT).
Quindi, basandosi su ciò che si vede: per la Tartaruga ha vinto lei, per Achille ha vinto lui, per due giudici ha vinto la tartaruga e per un terzo giudice ha vinto Achille.
La quinta figura risponde alla quinta domanda, ossia cosa succede alla partenza nei vari sistemi cambiando lo schema?
Tutti i sistemi (t; t'T; t''A) concordano che Achille e la Tartaruga si incontrano al traguardo (indicato come evento Z).
Il disaccordo riguarda, invece, la partenza.
Per il sistema dei giudici Achille e la Tartaruga partono (tP) e arrivano insieme al traguardo (tF).
Per il sistema della Tartaruga, Achille è partito (t'A) prima di Lei (t'T).
Per il sistema di Achille, la tartaruga è partita (t''T) prima di Lui (t''A).
L'ultima figura mostra che cosa vedono direttamente i vari personaggi, nel terzo schema di partenza.
La Tartaruga vede Achille partire (t'lA) dopo di lei (t'T) ed Achille vede la Tartaruga (t''lT) partire dopo di lui (t''A), ossia l'esatto contrario di ciò che misurano i loro sistemi di riferimento.
Due giudici (GT e GF) vedono partire prima la Tartaruga e poi Achille, mentre il terzo giudice (GA) vede partire prima Achille (tP) e poi la Tartaruga (tlT).
Ora vado a leggere la soluzione ed i commenti, anche per controllare di non aver commesso qualche errore.
rileggi bene il nuovo testo... ho cambiato il compito dei giudici in modo da non creare situazioni un po' confuse.
detto in parole povere i giudici di partenza fanno partire gli orologi a un tempo stabilito (non possono guardare quando partono i concorrenti, ossia prendono per buona una partenza simultanea). Quando i concorrenti arrivano i due giudici di arrivo si occupano solo di cronometrare il tempo del proprio concorrente. E' solo il giudice di partenza che può anche GUARDARE cosa succede ai due concorrenti.
La stessa cosa capita nell'ultimo caso: non si può mettere in discussione la partenza da parte dei due giudici di partenza, ma solo quella del giudice di arrivo che può VEDERE la partenza...
Ho semplificato la trattazione, altrimenti si creavano situazioni un po' ambigue... come potrai vedere da solo se ammetti che non TUTTI i giudici siano corretti...
13 commenti
Ci sto lavorando...
Al momento posso lavorarci solo in modo discontinuo e poiché mi rendo conto di essere lento nell’elaborazione delle figure avrei deciso di postare la mia soluzione divisa in 3 parti via via che completo le figure. In tal modo chi volesse potrebbe anche trarre spunto dalla mia impostazione (che spero corretta) per proseguire mentre porto avanti il resto. Non mi riferisco a Paolo che sappiamo bene essere un esperto di Minkowski e di RR e che di certo ha già risolto il tutto.
PARTE 1 – fianco a fianco
Parto dalla considerazione che l’evento “arrivo al traguardo della tartaruga e di Achille” è simultaneo nel sistema di riferimento dei giudici (sistema in quiete). Quindi riporto sul classico grafico di Minkowski X-t (in nero) i punti che corrispondono all’arrivo della tartaruga e di Achille (istante t). Essi saranno posizionati all’istante Tarr sulle rispettive linee d’universo dei giudici GP, GT e GA (in verde), con la distanza tra GT e GA uguale alla distanza GP-GT come suggerisce lo schema del testo. Aggiungo nella figura che segue anche la linea della velocità della luce (in giallo) e inclinata di 45° come vuole Minkowski, che servirà dopo.
Sia la tartaruga che Achille rappresentano invece sistemi in moto (uniforme) e pertanto occorre riportare gli assi X-t dei loro rispettivi sistemi di riferimento. La tartaruga è più lenta e quindi la “forbice” tra gli assi del suo sist. di riferimento è più aperta (assi viola) che nel caso di Achille (assi rossi). Vedi fig.1.
fig1
Trasporto ora il punto viola, cioè l’evento “arrivo della tartaruga” nel sistema di riferimento di Achille, tracciando la parallela all’asse XA (linea rossa tratteggiata) ed ottenendo il punto viola sull’asse dei tempi “achillei”. Poi riporto il punto rosso, cioè l’evento “arrivo di Achille” nel sist. di rif. della tartaruga tracciando la parallela all’asse XT (linea tratteggiata viola) ed ottenendo il punto rosso sull’asse dei tempi “tartarugheschi”. Vedi fig. 2.
fig.2
Quindi si vede che nel sist. di Achille vince Achille (la tartaruga arriva dopo) e nel sist. di rif. della tartaruga anche (Achille arriva prima), come indicano le rispettive posizioni dei punti rosso e viola.
Per capire cosa vedono giudici ed atleti occorre considerare i percorsi della luce rispetto a chi percepisce le immagini. Giudice GP: traccio le perpendicolari alla linea gialla dai pti che rappresentano l’arrivo della tartaruga e di Achille ed ottengo i pti 1 e 2, il giudice GP vede arrivare prima la tartaruga e poi Achille.
Giudice GT: l’intersezione con la perpendicolare alla linea gialla dal pto che rappresenta l’arrivo di Achille fornisce la posizione del pto 3 mentre l’arrivo della tartaruga su questa linea d’universo è il pto viola, il giudice GT vede arrivare prima la tartaruga e poi Achille.
Giudice GA: l’intersezione con la parallela alla linea gialla dal pto che rappresenta l’arrivo della tartaruga fornisce la posizione del pto 4 mentre l’arrivo di Achille su questa linea d’universo è il pto rosso, il giudice GA vede arrivare prima Achille e poi la tartaruga. La stessa linea prolungata fino all’asse del tempo achilleo (tA) fornisce il pto 5, e quindi Achille vede la tartaruga tagliare il traguardo dopo di lui.
L’intersezione tra la perpendicolare alla linea gialla condotta dal pto che rappresenta l’arrivo di Achille e l’asse del tempo tartarughesco (tT) fornisce il pto 6, e quindi la tartaruga vede Achille tagliare il traguardo dopo di lei. vedi fig.3.
fig.3
A seguire la parte la parte 2 (appena pronta).
buon lavoro Guido!!!!
ecco la parte 2.
Rispetto al caso precedente occorre spostare GT con la sua linea d’universo a sin di GP, mantenendo invariata la distanza da GP stesso, come dice lo schema del testo. Gli assi del sistema tartarughesco ora devono essere ribaltati rispetto agli assi del sistema in quiete (in nero) poiché la tartaruga si sposta nel verso contrario a quello di Achille.
Con la medesima procedura utilizzata in fig. 2 si ottengono ora il pto viola sull’asse rosso e pto rosso sull’asse viola che rappresentano, rispettivamente, gli eventi “arrivo della tartaruga” rispetto al sistema achilleo e “arrivo di Achille” rispetto al sistema tartarughesco. Vedi fig. 4
Quindi si vede che nel sist. di Achille vince Achille (la tartaruga arriva molto dopo) mentre nel sist. di rif. della tartaruga vince la tartaruga (Achille arriva dopo), come indicano le rispettive posizioni dei punti rosso e viola.
Per capire cosa vedono giudici ed atleti considero i percorsi della luce rispetto a chi percepisce le immagini, come prima.
Giudice GP: traccio la perpendicolare alla linea gialla dal pto che rappresenta il momento in cui egli vede arrivare Achille ed ottengo il pto 2, l’intersezione con la parallela alla linea gialla è il pto 1 che rappresenta il momento in cui egli vede arrivare la tartaruga, quindi il giudice GP vede arrivare prima la tartaruga e poi Achille.
Giudice GT: con le medesime rette si ottiene l’intersezione 3 che rappresenta il momento in cui il giudice vede arrivare Achille mentre l’arrivo della tartaruga su questa linea d’universo è il pto viola, il giudice GT vede arrivare prima la tartaruga e poi Achille.
Giudice GA: l’intersezione con la parallela alla linea gialla dal pto che rappresenta l’arrivo della tartaruga fornisce la posizione del pto 4 mentre l’arrivo di Achille su questa linea d’universo è il pto rosso, il giudice GA vede arrivare prima Achille e poi la tartaruga. La stessa linea prolungata fino all’asse del tempo achilleo (tA) fornisce il pto 5 (mi finisce fuori grafico ma se mi rimetto a disegnare tutto si fa notte…), e quindi Achille vede la tartaruga tagliare il traguardo ben dopo di lui.
L’intersezione tra la perpendicolare alla linea gialla condotta dal pto che rappresenta l’arrivo di Achille e l’asse del tempo tartarughesco (tT) fornisce il pto 6, e quindi la tartaruga vede Achille tagliare il traguardo dopo di lei. vedi fig. 5.
[caption id="" align="alignnone" width="494"]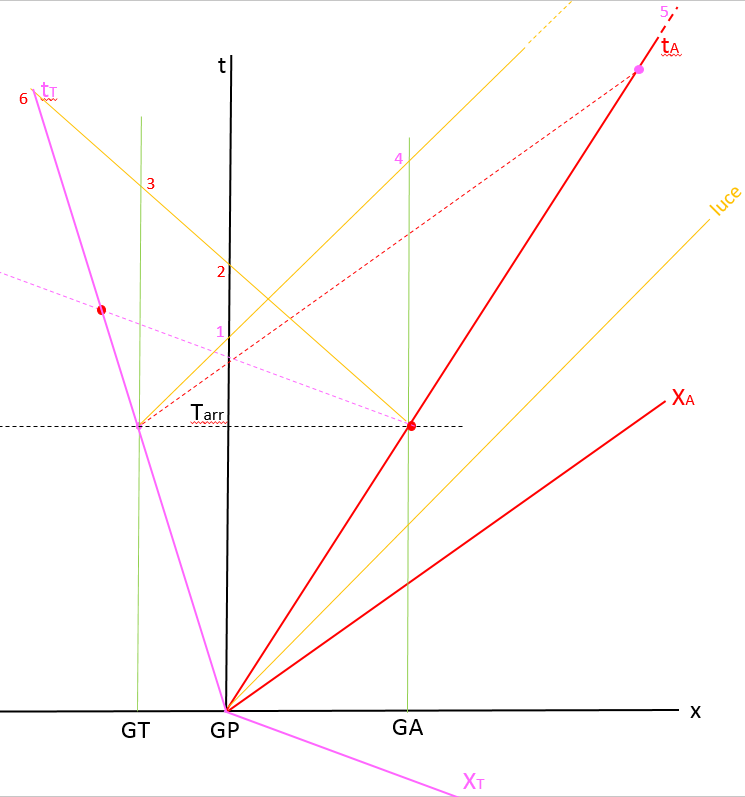 fig.5[/caption]
fig.5[/caption]
Ora vedo cosa riesco a cavar fuori per la terza ed ultima parte.
Lo sapevo, non m'è riuscito di inserire la fig. 4.
[caption id="" align="alignnone" width="460"]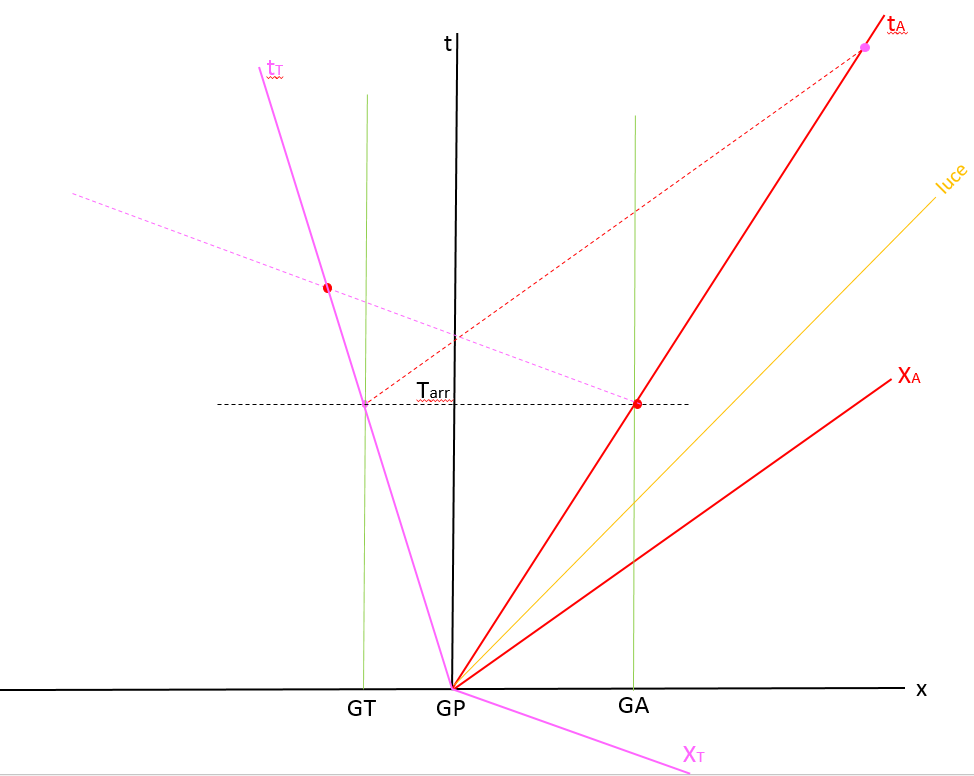 fig. 4[/caption]
fig. 4[/caption]
Quando hai finito, fai uno schemino che indichi cosa dicono i tre giudici e Achille e la Tartaruga in ogni singolo caso. Così sarà più facile controllare il risultato...
Ecco la terza ed ultima parte. In fondo riassumo tutti i miei risultati.
PARTE 3
Rispetto al caso iniziale riposiziono l’origine dei rispettivi assi di riferimento concordemente con le partenze separate in GT e GA . Achille inoltre si muove verso sin mentre la tartaruga verso ds, quindi ruoto gli assi del sistema di riferimento di Achille in senso opposto. Si vede che i 2 concorrenti arrivano in perfetta contemporaneità sull’asse t del sistema in quiete (pallino nero) nonché del giudice GF. Anche per i due sistemi di riferimento dei concorrenti tutto torna, c’è contemporaneità e quindi i pallini viola e rosso si sovrappongono a quello nero. L’osservazione diretta conferma tutto, infatti anche sulle linee d’universo dei giudici GT e GA i pallini, proiettati al solito modo secondo la linea gialla della luce, coincidono (punti 1 e 2) tanto per GA che per GT. Vedi fig. 6
[caption id="" align="alignnone" width="451"]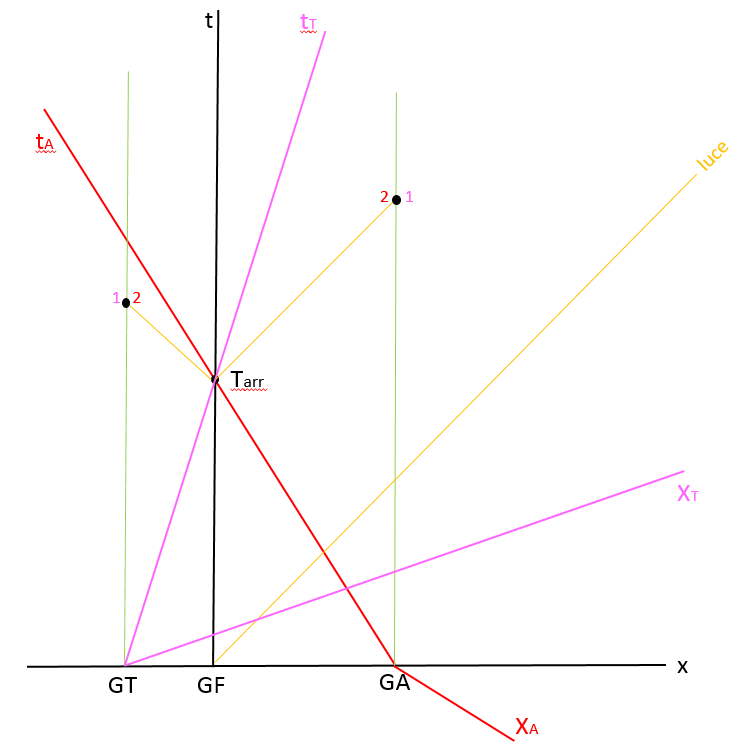 fig.6[/caption]
fig.6[/caption]
Per controllare le partenze occorre riportare il punto GT della partenza della tartaruga nel sistema di riferimento di Achille (assi rossi), ottenendo il pto PT’ (pallino viola) e analogamente riportando il punto GA (partenza di Achille) nel sist. di rif. della tartaruga (assi viola) si ottiene il pto PA’ (pallino rosso).
Per i 3 giudici l’evento della partenza è simultaneo, mentre nel sistema della tartaruga Achille è partito prima. Anche nel sistema di Achille la tartaruga è partita prima.
Il giudice GF vede partire la tartaruga all’istante 3, il giudice GA all’istante 5 e Achille la vede partire all’istante 4.
Il giudice GT vede la partenza di Achille all’istante 8, la tartaruga lo vede partire all’istante 7. Vedi fig. 7
[caption id="" align="alignnone" width="486"]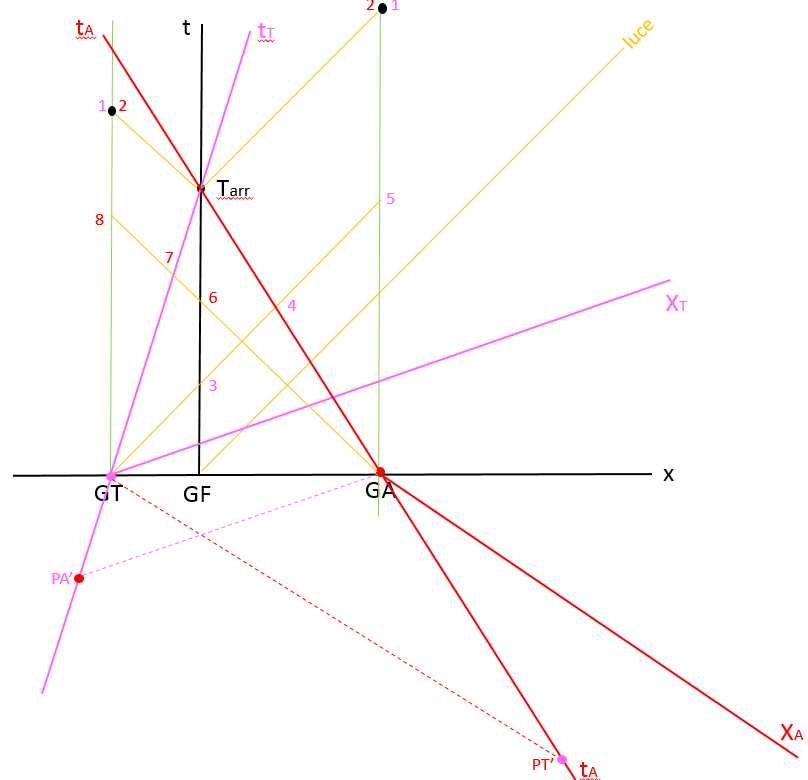 fig.7[/caption]
fig.7[/caption]
RIASSUMENDO
Se ho disegnato e ragionato correttamente dovremmo avere le seguenti riposte:
PARTE 1
Nel sistema di Achille vince Achille
Nel sistema della tartaruga vince sempre Achille
Verifica visiva: il giudice GP vede arrivare prima la tartaruga, il giudice GT vede arrivare prima la tartaruga e il giudice GA vede arrivare prima Achille. La tartaruga vede Achille arrivare dopo di lei, Achille la vede invece arrivare dopo di lui.
PARTE 2
Nel sistema di Achille vince Achille
Nel sistema della tartaruga vince la tartaruga
Verifica visiva: il giudice GP vede arrivare prima la tartaruga, il giudice GT vede arrivare prima la tartaruga e il giudice GA vede arrivare prima Achille. La tartaruga vede Achille arrivare dopo di lei, Achille la vede invece arrivare dopo di lui.
PARTE 3
Nel sistema di Achille, della tartaruga e dei 3 giudici l’arrivo dei 2 concorrenti è simultaneo, la verifica visiva conferma la simultaneità.
Controllo partenze:
Nel sistema di Achille la tartaruga è partita prima di lui.
Nel sistema della tartaruga invece è stato Achille a partire prima di lei.
Verifica visiva: il giudice GF vede partire prima la tartaruga, il giudice GT vede partire prima la tartaruga e il giudice GA vede partire prima Achille. La tartaruga vede Achille partire dopo di lei, Achille la vede invece partire dopo di lui.
caro Guido...
avevo valutato male i giudici... comunque controlla adesso la tua risposta con la mia e vediamo se tutto torna... potrei aver fatto anch'io un po' di confusione... adesso dovrebbe essere giusta la risposta...
Ho controllato con la risposta, mi sembra che tutto torni.
Caro Enzo, prima di leggere i commenti e la soluzione, vorrei provare a rispondere anch'io alle domande del quiz.
Come al solito per i sistemi di riferimento userò le linee di simultaneità (quando gli orologi sincronizzati di quel sistema segnano lo stesso tempo):
nere e parallele all'asse x per i giudici;
blu e parallele all'asse x' per la Tartaruga;
rosse e parallele all'asse x'' per Achille,
La prima figura risponde alla prima domanda, ossia chi vince nei vari sistemi ?
Per il sistema dei giudici Achille e la Tartaruga arrivano insieme al traguardo al tempo tF (vedi linea di simultaneità nera).
Per il sistema della Tartaruga, quando lei raggiunge il traguardo (t'T) Achille l'ha già raggiunto (tempo t'A, linea di simultaneità blu).
Per il sistema di Achille, la tartaruga raggiunge il traguardo (t''T linea di simultaneità rossa) dopo che lui è già arrivato (t''A ).
Quindi per entrambi vince Achille.
Il disaccordo tra giudici e atleti, dipende ovviamente dal fatto che ogni sistema ha le sue linee di simultaneità!
La seconda figura mostra che cosa vedono direttamente i vari personaggi.
Questa volta, a differenza di prima, la Tartaruga vede Achille raggiungere il traguardo (t'lA) dopo di lei (t'T).
Achille vede la Tartaruga raggiungere il traguardo (t''lT) dopo di lui (t''A).
Due giudici (Gp e GT) vedono arrivare al traguardo prima la Tartaruga e poi Achille, mentre il terzo giudice (GA) vede arrivare prima Achille (tF) e poi la Tartaruga (tlT).
Quindi, basandosi su ciò che si vede: per la Tartaruga ha vinto lei, per Achille ha vinto lui, per due giudici ha vinto la tartaruga e per un terzo giudice ha vinto Achille.
C'è un totale disaccordo, ma d'altronde la visione diretta non tiene conto del tempo impiegato dalla luce per percorrere la distanza che ci separa dall'evento che si osserva.
Nella figura ho anche mostrato la luce che parte dal punto di partenza, che mostra il ritardo con cui raggiunge prima il giudice GT e poi il giudice GA.
La terza figura risponde alla terza domanda, ossia chi vince nei vari sistemi cambiando lo schema di partenza?
Per il sistema dei giudici Achille e la Tartaruga arrivano insieme al traguardo (al tempo tF).
Per il sistema della Tartaruga, Achille raggiunge il traguardo (t'A) dopo che lei è già arrivata (t'T).
Per il sistema di Achille, la tartaruga raggiunge il traguardo (t''T) dopo che lui è già arrivato (t''A).
Quindi per entrambi sono loro i vincitori.
segue
La quarta figura mostra che cosa vedono direttamente i vari personaggi, nel secondo schema di partenza.
La Tartaruga vede Achille raggiungere il traguardo (t'lA) dopo di lei (t'T) ed Achille vede la Tartaruga raggiungere il traguardo (t''lT) dopo di lui (t''A).
Due giudici (GT e GP) vedono arrivare al traguardo prima la Tartaruga e poi Achille, mentre il terzo giudice (GA) vede arrivare prima Achille (tF) e poi la Tartaruga (tlT).
Quindi, basandosi su ciò che si vede: per la Tartaruga ha vinto lei, per Achille ha vinto lui, per due giudici ha vinto la tartaruga e per un terzo giudice ha vinto Achille.
La quinta figura risponde alla quinta domanda, ossia cosa succede alla partenza nei vari sistemi cambiando lo schema?
Tutti i sistemi (t; t'T; t''A) concordano che Achille e la Tartaruga si incontrano al traguardo (indicato come evento Z).
Il disaccordo riguarda, invece, la partenza.
Per il sistema dei giudici Achille e la Tartaruga partono (tP) e arrivano insieme al traguardo (tF).
Per il sistema della Tartaruga, Achille è partito (t'A) prima di Lei (t'T).
Per il sistema di Achille, la tartaruga è partita (t''T) prima di Lui (t''A).
L'ultima figura mostra che cosa vedono direttamente i vari personaggi, nel terzo schema di partenza.
La Tartaruga vede Achille partire (t'lA) dopo di lei (t'T) ed Achille vede la Tartaruga (t''lT) partire dopo di lui (t''A), ossia l'esatto contrario di ciò che misurano i loro sistemi di riferimento.
Due giudici (GT e GF) vedono partire prima la Tartaruga e poi Achille, mentre il terzo giudice (GA) vede partire prima Achille (tP) e poi la Tartaruga (tlT).
Ora vado a leggere la soluzione ed i commenti, anche per controllare di non aver commesso qualche errore.
Paolo
Paolo
caro Paolo,
rileggi bene il nuovo testo... ho cambiato il compito dei giudici in modo da non creare situazioni un po' confuse.
detto in parole povere i giudici di partenza fanno partire gli orologi a un tempo stabilito (non possono guardare quando partono i concorrenti, ossia prendono per buona una partenza simultanea). Quando i concorrenti arrivano i due giudici di arrivo si occupano solo di cronometrare il tempo del proprio concorrente. E' solo il giudice di partenza che può anche GUARDARE cosa succede ai due concorrenti.
La stessa cosa capita nell'ultimo caso: non si può mettere in discussione la partenza da parte dei due giudici di partenza, ma solo quella del giudice di arrivo che può VEDERE la partenza...
Ho semplificato la trattazione, altrimenti si creavano situazioni un po' ambigue... come potrai vedere da solo se ammetti che non TUTTI i giudici siano corretti...