Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo

 

Grandezze fisiche

Per parlare di grandezze fisiche, proprio come il nostro amico Momento Angolare, è necessario dividerle, innanzitutto, in due grandi categorie, sulla base delle loro caratteristiche intrinseche, esprimibili con particolari notazioni matematiche.

Non spaventatevi di questa frase un po’ contorta, mi spiegherò velocemente. Prendiamo due grandezze tipiche della fisica, come la massa e la velocità. La prima è esprimibile con un numero, uno scalare, in una certo sistema di misura, ed è completamente individuata. Essa prende il nome di grandezza scalare. La seconda invece, ha bisogno di almeno tre caratteristiche per essere definita in modo univoco. Innanzitutto, un numero (che chiamiamo modulo) che ne indichi la grandezza (analogamente alle grandezze scalari), poi di una direzione e infine di un verso. La chiamiamo grandezza vettoriale.

In realtà, quando diciamo che una macchina viaggia a 100 km/h (grandezza di tipo scalare o modulo), dobbiamo anche indicare in quale direzione sta andando (sull’autostrada, sulla tangenziale, sul Corso principale, sul lungomare,…). La stessa velocità (come numero) può essere ottenuta su qualsiasi percorso e quindi va definito il percorso. Non basta ancora, però. Dobbiamo anche sapere se la macchina va dal centro verso il mare o in senso contrario. Si deve, quindi, aggiungere anche il verso di percorrenza. Spesso e volentieri, vi è anche bisogno di una quarta caratteristica: il punto di applicazione.  In altre parole, sappiamo che la velocità è di “tot” km/sec, che si sta ottenendo sulla strada che porta alla spiaggia e che va dal centro al mare, ma vogliamo anche sapere a che macchina si riferisce! Ci sono moltissime macchine che possono avere le stesse caratteristiche definite precedentemente.

Vi siete accorti che ho usato molte parole per descrivere questo tipo di grandezza fisica ed è sicuramente preferibile farci dare in prestito dalla matematica e dalla geometria una rappresentazione simbolica che unisca tutte e quattro le caratteristiche della velocità.

Questa rappresentazione simbolica si chiama vettore e le grandezze fisiche che ne fanno uso si chiamano grandezze vettoriale.  Lo possiamo applicare a un punto P che potrebbe essere un’entità fisica come ad esempio un corpo di massa m. Tuttavia, ripeto ancora, la grandezza scalare massa è del tutto estranea al vettore, al verso e alla intensità del movimento da lui indicato. Essa dipende solo dalla macchina, ossia -ancora meglio- definisce solo una caratteristica della macchina, qualcosa strettamente legata al suo peso.  Al limite, sarà trascinata, in modo “inerte”, dalla grandezza vettoriale. Riflettendo un attimo abbiamo già introdotto la quantità di moto… Ma, ci torneremo sopra a tempo debito.

Numeri e grandezze scalari

Prima di farci prendere per mano dai vettori, capiamo subito bene la differenza tra numero e grandezza scalare. Sembrano la stessa cosa, ma non lo sono… Una grandezza scalare è esprimibile con un numero, ma ha delle dimensioni in un certo sistema di misura. E’ una caratteristica fisica, esprimibile matematicamente con un semplice numero, ma non è un numero fine a se stesso. Se dico che una “pera” pesa 1 kg o che ha un volume di 100 cm³, conferisco all’oggetto "pera" una certa caratteristica (scalare). Se invece dicessi 5 pere, assocerei all’oggetto "pera" l’informazione relativa soltanto al numero di pere, senza stabilirne alcuna caratteristica intrinseca: potrebbero essere di massa diversa, di forma diversa, di volume diverso, ma non interesserebbe assolutamente. Rimarrei nel puro mondo della matematica: contare, sommare, moltiplicare numeri e nulla più. Invece della pera, ovviamente, potrei usare mele, scatole, stelle, elettroni, poco importa. Ogni grandezza scalare dona, invece, un’informazione in più su una certa entità fisica.

Sono grandezze scalari: la temperatura, la massa, la carica elettrica, la pressione, la densità, il volume, la lunghezza d’onda, la frequenza, il lavoro, ecc., ecc.

Sono, invece, grandezze vettoriali: la velocità, l’accelerazione, la forza, la quantità di moto, il momento angolare, il momento di una forza, il campo gravitazionale, ecc., ecc.

Disegniamo un vettore

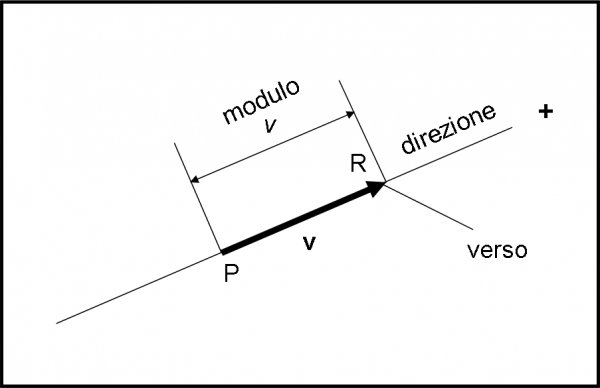
Prima di applicare il vettore alle grandezze fisiche che ne hanno bisogno, descriviamolo molto accuratamente come entità puramente matematica. In Fig. 1 la retta indica la direzione, la freccia il verso, la lunghezza del segmento PR il modulo del vettore. Questa definizione è indipendente dalla grandezza fisica che andrà a rappresentare. Il punto P è il suo punto di applicazione. Attenzione al modo di scrivere un vettore. Esso lo indicheremo sempre con una lettera in grassetto (v). La stessa lettera, in corsivo, starà a indicare il modulo del vettore (v), ossia la sua parte numerica o -se preferite- la sua parte scalare. E’ una nostra scelta, seguita normalmente, molto utile per non confondere scalari con vettori.

Operazioni tra grandezze 

Le grandezze scalari e vettoriali applicate agli oggetti dell’Universo permettono di descrivere le sue leggi e di capire come i vari attori stanno recitando. In poche parole, le grandezze fisiche, unite ai corpi materiali (ma non solo) a cui sono applicate, rappresentano la Fisica o, se preferite, l’Astrofisica.

Le grandezze vanno definite e capite molto bene, dato che ognuna di esse dice qualcosa di più sul corpo celeste. Senza conoscerle tutte (o quasi) diventerebbe impossibile stabilire che cos’è quel corpo e che cosa è in grado di fare o sta già facendo.

Le grandezze fisiche possono eseguire operazioni tra di loro ed è bene impararle perfettamente per poterle utilizzare normalmente quando ne avremo bisogno, così come abbiamo imparato le operazioni sui numeri in matematica.

Operazioni tra grandezze scalari

Ovviamente, anche le grandezze scalari sanno fare operazioni tra di loro e portare a drastici cambiamenti. Ma, essendo solo e soltanto dei numeri, le operazioni sono solo quelle che si applicano ai numeri, ossia ciò che noi abbiamo chiamato, molto semplicisticamente, matematica. Non c’è quindi bisogno di spiegare cosa permettono di fare. Ad esempio, se conosco la massa di un corpo e anche il suo volume, sono in grado di determinare una nuova grandezza (sempre scalare) che è la densità. Basta infatti dividere la massa per il volume e il gioco è fatto. Ribadisco ancora, in questo caso ho operato con grandezze fisiche scalari che sono rappresentate da numeri, ma che non sono numeri puri. Una massa di 5 (grammi) divisa per un volume di 2 (cm³) ci regala una densità di 2.5 (g/cm³), ma ogni grandezza ha la sua unità di misura, ossia identifica una ben definita caratteristica della materia. Se, invece divido una massa di 5 (grammi) per il numero 2 (fine a se stesso), non faccio altro che dividere a metà la massa : il risultato è solo e soltanto una massa dimezzata. So che sembrano sciocchezze, ma saper distinguere tra uno numero (matematica) e il numero che indica una grandezza scalare (fisica) è più che fondamentale nel mondo della fisica. E, prima o poi, ce ne accorgeremo…

In ogni modo, le operazioni svolte su grandezze scalari portano solo e soltanto a grandezze scalari.

Operazioni con le frecce: attenzione… possono pungere!

Le cose si complicano un poco, invece, quando si considerano le grandezze vettoriali. Esse possono agire insieme agli scalari oppure tra di loro.

Quando agiscono con uno scalare (che sia grandezza scalare oppure soltanto un  numero) hanno sempre il sopravvento. In parole semplicissime, se moltiplichiamo un vettore per un numero, il risultato è sempre un vettore. Il numero sarà solo in grado di aumentare la lunghezza o la grandezza del vettore (il suo modulo) o di incollargli un certa grandezza scalare, ma non di influenzare la direzione e il punto di applicazione. Il segno dello scalare (se lo consideriamo con segno) può indicare il verso del vettore. Se è positivo, il vettore non cambia verso, se è negativo, il verso è esattamente l’opposto di prima. Non tutti gli scalari hanno un segno (come la massa) e quindi non influenzano assolutamente né direzione né verso del vettore per cui sono moltiplicati.

Ripeto ancora: se, ad esempio, associo un grandezza scalare a un vettore, ottengo un nuovo vettore che ha un significato diverso. Ad esempio, la grandezza scalare massa moltiplicata per il vettore velocità da luogo nientedimeno che alla quantità di moto, uno dei capisaldi della meccanica classica (e non solo, come vedremo nell’atomo di Bohr). Se invece moltiplico il numero 3 per la velocità, ottengo un nuovo vettore velocità che rimane invariato tranne che per la sua lunghezza, pari a tre volte quella di partenza. Cambia il valore numerico della velocità, ma non cambia il tipo di grandezza vettoriale. Quest’ultimo caso lo vediamo in Fig. 2, per un numero positivo e uno negativo (3 e -3).

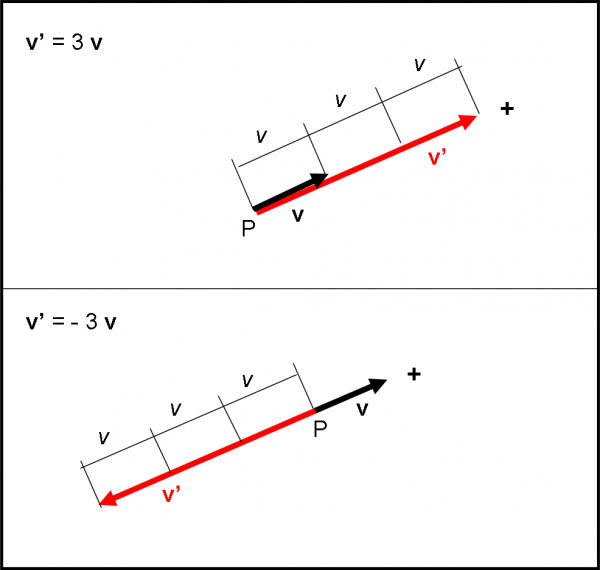
Riassumendo: se moltiplico (o divido) uno scalare per un vettore, lo scalare, che sia numero o grandezza scalare, entra tranquillamente all’interno del vettore e va a moltiplicare (o a dividere) solo il valore numerico del vettore (il modulo). Tra numeri si capiscono benissimo!

Il modulo del vettore prodotto tra scalare n e vettore v sarà dato da nv, mentre il vettore sarà indicato con nv. Se questo vettore fosse nuovamente moltiplicato per un’altra grandezza scalare m, otterremmo un vettore mnv, di modulo mnv.

Scomponiamo un vettore

Prima di eseguire le operazioni tra vettori è bene imparare come un vettore possa essere scomposto su un piano cartesiano qualsiasi. Consideriamo, nella Fig. 3, un punto P e tracciamo gli assi x e y che hanno proprio origine in P (per comodità, dato che potrei usare qualsiasi tipo di assi cartesiani).

Se il punto P restasse fermo, potrei dire che non gli è associato nessun vettore. Sarebbe, però, molto meglio dire che gli è stato applicato un vettore nullo. Perché complicarci così la vita? presto detto: in Natura niente è mai veramente fermo e se un punto appare fermo (in un certo sistema di riferimento) vuol dire che agiscono più vettori su di lui, ma che, in qualche modo si abbracciano tra loro dando luogo a un vettore nullo. Pensateci bene sopra e vedrete che non ho detto assolutamente una cosa banale. Ho solo accennato all’equilibrio o -se preferite- alla statica…

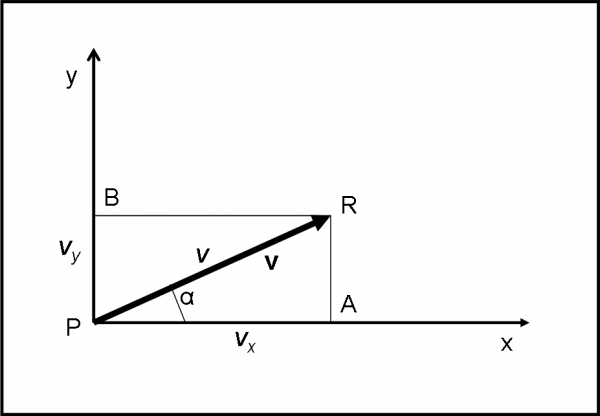
Associamo a P (che potrebbe essere un corpo fisico  come una particella o una stella) il vettore v. Il suo modulo è v ed è proprio la lunghezza PR. La direzione è quella della retta PR e il verso è quello che va da P a R.

Occupiamoci, per un attimo, del vettore PR come se fosse un segmento del piano x,y. In altre parole, occupiamoci solo del suo modulo v. Come già detto, esso è dato dalla lunghezza del segmento PR. Sappiamo benissimo calcolare matematicamente le coordinate di un segmento rispetto a un sistema cartesiano (ripassate la matematica…). Tracciamo le perpendicolari dai punti estremi del segmento ai due assi. Otteniamo i due segmenti PA e PB.  Il primo, v_x, non è altro che la differenza tra le ascisse del segmento, ossia x_R-x_P, il secondo v_y è la differenza delle ordinate y_R-y_P. Quanto vale la lunghezza v del segmento PR? Conoscendo le due coordinate PA e PB è immediato ricavarla dal teorema di Pitagora:

v = (PA² + PB²)^1/2  = ((x_R-x_P)² + (y_R-y_P)²)^1/2 = (v_x² + v_y²)^1/2     …. (1)

Analogamente, potremmo anche legare le due coordinate PA e PB al modulo v, attraverso la trigonometria:

PA = v_x = v cos α

PB = v_y = v sen α     …..  (2)

Possiamo dire che conoscendo le coordinate del segmento, è immediato calcolare il modulo del vettore PR e viceversa.

Aiutanti indispensabili: i versori

Potremmo anche ritenerci contenti. Però, è molto meglio introdurre due vettori  molto particolari che caratterizzino gli assi cartesiani x e y. Essi hanno come modulo il valore unitario (qualsiasi sia l’unità di misura che vogliamo assegnare alle coordinate), hanno la direzione degli assi e hanno il verso diretto verso destra (parte positiva dell’asse x ) e verso l’alto (parte positiva dell’asse y). Non hanno un punto di applicazione, dato che sono sempre disponibili, a seconda delle necessità del vettore che devono aiutare. Indichiamo con i quello relativo all’asse x e con j quello relativo all’asse y. Li chiamiamo versori degli assi coordinati. Per come sono stati definiti, i loro moduli saranno: i = 1, j = 1. Li vediamo nella Fig. 4.

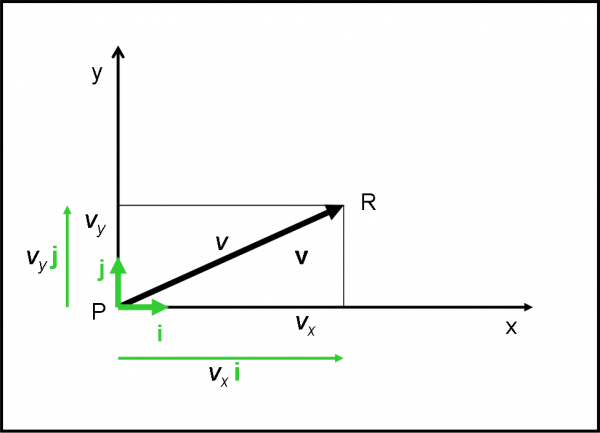
Da quanto abbiamo imparato nella moltiplicazione di un vettore per uno scalare, possiamo definire un vettore che sia il prodotto tra lo scalare v_x e il versore i. Scriviamo questo vettore come v_xi, di modulo v_x 1 = v_x. PB porta a un analogo vettore v_yj. Insomma, un vettore v può essere rappresentato molto bene da due vettori che utilizzino i versori i e j e le componenti lungo gli assi del modulo v.

Perché lo facciamo? Dato che ormai sappiamo come legare il modulo v di un vettore v con le coordinate v_x e v_y dei vettori v_xi e v_yj (attraverso le relazioni (1) e (2)), potremmo in ogni momento e per ogni vettore introdurre questi due vettori “ausiliari” scegliendo “ad hoc” gli assi cartesiani. L’importante è che i e j siano ortogonali tra loro. Abbiamo detto ben poco, ma il concetto è che esiste una relazione ben definita tra i moduli di questi tre vettori, che sfrutta il teorema di Pitagora e/o un minimo di trigonometria. Per il momento, abbandoniamo i versori e i vettori ausiliari. Li useremo tra poco…

Somma e differenza di vettori

Occupiamoci, adesso, di definire la somma di due vettori, che per semplicità disegniamo entrambi con lo stesso punto di applicazione P. Il vettore PR (v) va sommato al vettore PQ (u).

Innanzitutto, dichiariamo apertamente che la somma di due vettori è ancora un vettore. Sappiamo già molto bene come si costruisce graficamente il vettore somma (perfino la QED ha usato questa operazione per sommare le ampiezze). In Fig. 5, basta traslare il vettore u fino alla “punta” del vettore v. Tracciamo poi il vettore che parte dal punto P e arriva al punto R, ossia che parte dalla “coda” di v e arriva alla “punta” di u. Non abbiamo fatto altro che usare la ben più celebre regola del parallelogramma. Il vettore somma lo chiamiamo w e vale la relazione:

w = v + u

Per ottenere la differenza dei vettori (v - u), basta ribaltare il vettore u e farlo diventare -u e poi eseguire la somma tra v e -u. Cosa già dette e ridetto varie volte.

Possiamo anche dedurre immediatamente che l'operazione "somma di vettori" è un'operazione commutativa, ossia:

u + v = v + u

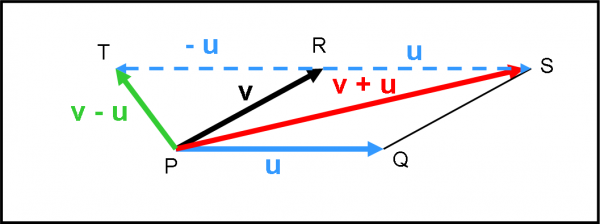
Graficamente, nessun problema, ma… quanto vale il modulo del nuovo vettore w = v + u?

Si potrebbe rispondere subito se i due vettori fossero  allineati (Fig. 6). La somma dei moduli dei due vettori sarebbe proprio uguale al modulo del vettore somma.  In altre parole, varrebbe anche:

w = v + u

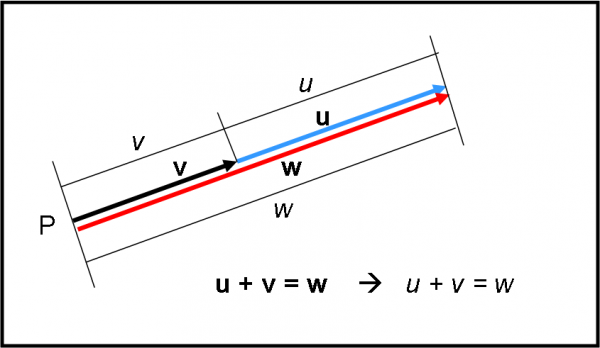
Attenzione, però. Questo è un caso estremamente particolare. In generale il modulo della somma NON è assolutamente uguale alla somma dei moduli. Si vede molto bene dalla regola del parallelogramma (Fig. 5). Il modulo della somma è la diagonale più lunga del parallelogramma. Sì, non sarebbe difficile determinare attraverso formule matematiche  la misura numerica della diagonale maggiore (o minore) di un rettangolo conoscendone i lati. Noi preferiamo farlo con quello che abbiamo appena introdotto, ossia attraverso i versori e i loro vettori ausiliari. Tornerà molto più utile e rapido (oltre che più … fisico). Per far ciò vediamo, prima, un altro caso particolare di somma di due vettori v e u.

Prendiamoli perpendicolari tra loro, come riportato in Fig. 7. Calcoliamone graficamente la somma, utilizzando le regole che abbiamo descritto precedentemente. Il vettore somma sarà w. Siamo di fronte a un rettangolo di lati u e v. La sua diagonale w si ricava immediatamente applicando il teorema di Pitagora. Ossia, otteniamo che:

w = (v² + u²)^1/2

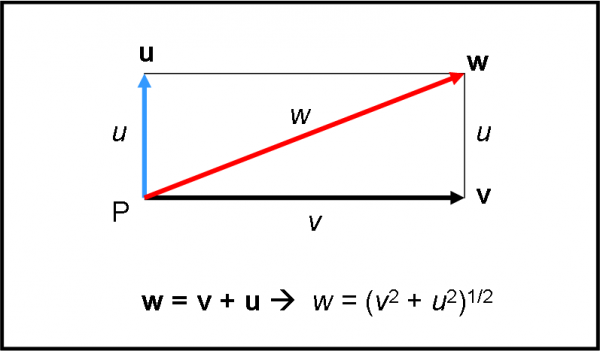
Usiamo i versori

Abbiamo visto, però, che per ogni vettore v è possibile ottenere due vettori tra loro ortogonali che lo rappresentino lungo le direzioni degli assi cartesiani, facendo uso dei versori i e j. In altre parole, abbiamo la Fig. 8 (identica alla Fig. 4).

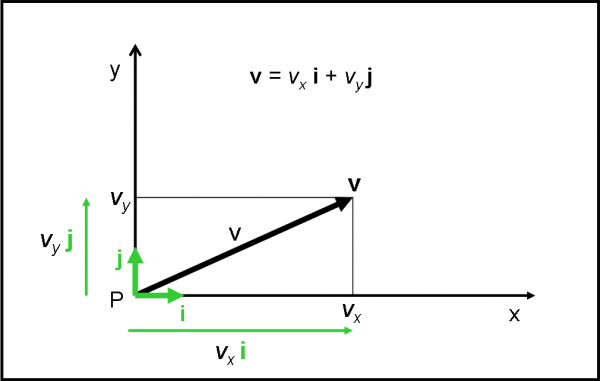
Per quanto abbiamo appena stabilito dalla Fig. 7, il vettore v è proprio la somma dei vettori v_xi e v_yj. Quindi possiamo scrivere:

v = v_xi + v_yj    …. (3)

la stessa cosa succederebbe se applicassimo in P il vettore u. Otterremmo nuovamente:

u = u_xi + u_yj   …. (4)

Ciò che abbiamo scritto è SICURAMENTE vero, dato che la somma di due vettori ortogonali come v_xi e v_yj è proprio v.

Utilizzando la (3) e la (4) possiamo, allora, scrivere, senza fare nessuna figura, la somma dei vettori u e v:

w = v + u = v_xi + v_yj + u_xi + u_yj = (v_x+u_x)i + (v_y + u_y)j = w_xi + w_yj

e, quindi:

w_x = v_x + u_x

w_y  =  v_y + u_y     …. (5)

Questa relazione ci dice una cosa importantissima:

Il vettore w, somma di due vettori u e v, può essere sempre rappresentato dalla somma di due vettori ortogonali (lungo due assi cartesiani scelti a piacere) che abbiano come modulo la somma dei moduli dei vettori v e u.

In breve: se conosciamo le componenti secondo due assi cartesiani qualsiasi dei vettori v e u, per ottenere le componenti del vettore somma basta sommare le componenti dei due vettori di partenza.

Abbiamo risolto il problema della somma di due (o più vettori) senza bisogno di fare una trattazione geometrica, ma utilizzando la scomposizione dei vettori lungo due assi cartesiani “comandati” dai versori i e j.

Potevamo farne a meno e risolvere il tutto con una bella figura. Tuttavia, questa descrizione ci permette di eseguire una scomposizione di un certo numero di vettori lungo due direzioni particolarmente interessanti (dal punto di vista fisico) e ottenere il modulo del vettore somma solo sommando i moduli dei vettori ottenuti dalla scomposizione. Chi volesse capire meglio questa motivazione, basta che pensi alla scomposizione dell’accelerazione di un corpo secondo due direzioni privilegiate, come quella tangenziale e normale alla traiettoria. In generale, quanto detto finora è già stato trattato (anche se un po’ diversamente) negli articoli sulla forza centrifuga. Questo (o quello) può essere un ripasso o una conferma…

Usiamo una semplice figura

Sapete, però, che, in fondo in fondo, sono una brava persona... Voglio, perciò, ottenere la stessa conclusione, utilizzando una rappresentazione grafica, sicuramente più intuitiva e immediata. Usiamo la Fig. 9, dove, nuovamente, vogliamo sommare i vettori v e u. Utilizziamo il metodo che trasla il secondo vettore e lo porta sulla “punta” del primo.

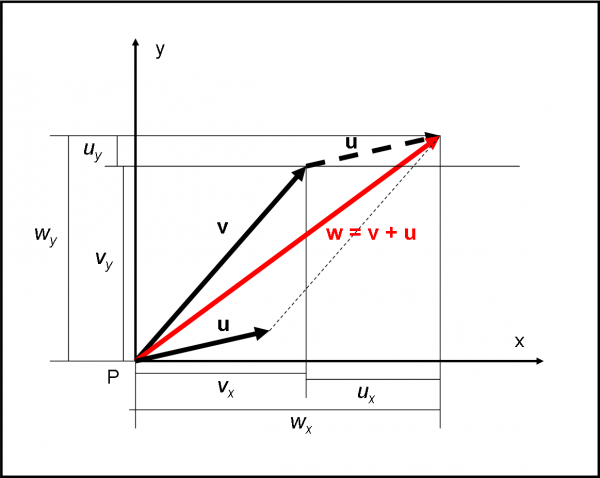
La figura mostra immediatamente che le due componenti w_x e w_y non sono altro che  (v_x + u_x) e (v_y + u_y).

Insomma, in un modo o nell’altro abbiamo risolto il problema di calcolare il modulo di un vettore che sia somma di due vettori. Usate quello che preferite, ma cercate di capirli bene tutti e due. Il primo è essenzialmente matematico e più generale; il secondo è essenzialmente geometrico e intuitivo.

Eseguiamo lo stesso calcolo nel caso di una differenza di vettori. Ovviamente le loro coordinate sono sempre le stesse, ossia:

v = v_xi + v_yj

e

u = u_xi + u_yj

Non ci resta che fare la differenza dei due vettori:

w = v - u = v_xi + v_yj - u_xi - u_yj = (v_x-u_x)i + (v_y - u_y)j = w_xi + w_yj

e, quindi:

w_x = v_x - u_x

w_y  =  v_y - u_y     …. (6)

Per trovare w, basta applicare, come sempre, il teorema di Pitagora:

w = (w_x² + w_y²)^1/2   …. (7)

I moduli sono ortogonali tra loro, proprio perché si riferiscono ai due versori ortogonali per costruzione. Posso tranquillamente applicare il teorema di Pitagora, come ho fatto sempre finora.

Ovviamente, si otteneva lo stesso risultato lavorando graficamente attraverso una Figura come la 9.

I versori, però, ci hanno permesso di usare solo semplici formule matematiche che possono applicarsi su un numero anche grande di vettori (magari sottraendone qualcuno e sommandone altri), senza dar luogo a una figura sempre più caotica e complicata…

In parole povere: se scomponiamo tutti i vettori che vogliamo sommare o sottrarre lungo degli assi cartesiani (uguali per tutti, ovviamente), ossia ricaviamo i moduli dei versori relativi a ciascun vettore, abbiamo ridotto tutto a una somma e/o differenza di moduli lungo il versore i e lungo il versore j. Il modulo finale di i e quello di j daranno le componenti del vettore finale.

Ad esempio:

v - u + t – s + z = w

si risolve trovando le coordinate di ogni singolo vettore e sommando quelle relative a i e quelle relative a j.

w = (v_xi + v_yj ) - (u_xi - u_yj) + (t_xi + t_yj) - (s_xi - s_yj) + (z_xi + z_yj)

Ho messo le parentesi per evidenziare i singoli vettori... scomposti (ma non ce n'era bisogno).

Raccogliendo i moduli di i e di j si ottengono subito le due componenti di w lungo i e j:

w = (v_x- u_x+ t_x - s_x+ z_x)i + (v_y - u_y+ t_y - s_y+ z_y)j

e, quindi:

w_x = v_x - u_x + t_x - s_x + z_x

w_y  =  v_y - u_y + t_y - s_y + z_y

Vi immaginate che caos sarebbe diventata la Fig. 9? E invece, in questo modo, abbiamo tutte le informazioni che vogliamo senza problemi. Una situazione del genere non è difficile da avere in fisica, quando su un certo oggetto agiscono molte forze o accelerazioni o velocità o qualsiasi tipo di grandezza vettoriale… e vogliamo trovare la grandezza vettoriale risultante. Ovviamente, non potrò sommare o sottrarre pere con mele, ma solo pere con pere e mele con mele…