Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo

Sembra quasi impossibile. Quando si parla di numeri, di “scalari”, le quattro operazioni fondamentali (che poi sono in realtà due dato che somma e differenza e prodotto e divisione sono praticamente la stessa cosa) si usano con pari frequenza e con difficoltà del tutto comparabili. Ed è abbastanza ovvio. Moltiplicare qualcosa vuol dire eseguire un certo numero di volte una somma, così come una divisione non è altro che eseguire un certo numero di volte una differenza. In altre parole, la somma (la differenza è una somma con segno invertito) ci permette di eseguire tutte e quattro le operazioni.

Ben diversa è invece la situazione per i vettori e, di conseguenza, per le grandezze vettoriali. Abbiamo già visto che la somma di vettori è qualcosa di banale, ma ha ben poco a che fare con la somma di due scalari. Coincide solo quando i vettori hanno la stessa direzione.

Se vi chiedessi: “Come si possono moltiplicare due vettori?”, qualcuno potrebbe pensare che è un po’ come per i scalari, ossia dovremmo sommare tante volte un vettore quanto ci dice l’altro… Che pasticcio… non avrebbe senso…. Insomma, non c’è niente da fare: scordatevi la relazione che c’è tra somma e prodotto nel mondo degli scalari e entrate senza rimpianti e senza idee preconcette nel mondo delle grandezze vettoriali. Lasciate anche alle spalle il prodotto di un vettore per uno scalare. Questa era ancora un’operazione legata al pensiero precedente: si prendeva il modulo del vettore (scalare), si moltiplicava per lo scalare (moltiplicazione “vecchio stampo”) e, solo dopo, il risultato veniva riconsegnato al vettore, che aveva solo guadagnato o perso qualcosa nella sua parte scalare.

L’abbiamo usata varie volte la volta scorsa, anche trafficando con i simpatici vettori unitari (i versori) e le componenti del vettore di partenza. Insomma, abbiamo solo scherzato… finora.

Il nuovo mondo, quello più usato nella meccanica classica, si mostra subito per quello che è: i prodotti tra vettori sono due, due operazioni completamente diverse tra loro. No, non siamo entrati nel Paese di Alice, siamo solo nel mondo delle grandezze vettoriali, quelle entità simboliche matematiche che hanno a loro disposizione tre armi diverse per combattere: modulo, direzione e verso, proprio come una spada!

Moltiplichiamo le spade

Non abbiate paura, vi capisco benissimo. Vi aspettereste che io scrivessi il prodotto di due vettori e vi dessi il risultato. Qualcosa del genere:

v u = ?

Mi spiace, non potrei proprio rispondere, perché quella scritta non ha alcun senso! Non ha assolutamente il significato di: “prendi il vettore v e sommalo a se stesso tante volte quanto dice il vettore u”. Anche perché cosa vorrebbe mai dire “tante volte quanto dice il vettore u” se u è un vettore che ha un modulo, una direzione e un verso? Lo potrei fare solo se u fosse uno scalare e allora ricadrei nel caso precedente: moltiplicherei il modulo di v per u e poi alla fine otterrei il vettore di modulo vu e di direzione e verso uguali a quelli di v.

Scusate se ripeto sempre le stesse cose e magari sembra che vi crei confusione. Normalmente, nessuno si cura di fare questi confronti e vi sbatte nel nuovo mondo senza nessuna preparazione mentale. Ne segue che i due mondi (scalare e vettoriale) sembrano due libri diversi e non due capitoli dello stesso libro. Sto solo dicendo cose ultra ovvie, che potrei cancellare tranquillamente, ma penso che il passaggio da operazioni tra scalari, tra scalari e vettori a quelle tra soli vettori abbiano bisogno di un certo intervallo di riflessione.

Adesso, però, può bastare e chiudiamoci la porta dietro, almeno per un po’.

La scrittura di sopra non ha senso, dato che non ha senso un’operazione indefinita tra due spade. Anche nella scherma esistono molti tipi di attacco e difesa. Nella simbologia delle grandezze vettoriali esistono solo due mosse: il prodotto scalare e il prodotto vettoriale. Li chiamiamo prodotti proprio perché hanno bisogno di un’azione reciproca delle due spade. Due attacchi o due difese o una parata e controparata, come preferite. Tuttavia, il concetto è sempre lo stesso: l’operazione prodotto indica un’azione da eseguire e comporta un certo tipo di risultato. Solo in questa definizione di massima si può vedere il ricordo delle operazioni tra scalari. Tuttavia, là si eseguivano solo degli “squallidi” conti, qui invece l’azione è variegata e complessa. Un po’ come una tenzone tra “villici” o tra “cavalieri”.

Fendente e tocco (prodotto scalare)

Devo ammettere che sono andato a documentarmi sulle azioni della scherma: il fendente è quel colpo che viene portato dall’alto in basso e che finisce col tocco. Direi che spiega abbastanza bene il primo prodotto vettoriale, quello scalare. Quel nome un po’ ambiguo (scalare) dà un po’ di fastidio, ma lo possiamo considerare come il risultato di un colpo vittorioso che annulla l’azione vettoriale e quindi conduce a una banale soluzione scalare. Basta! Vediamo di essere più seri.

Le due spade (forse per il fendente bisognerebbe dire sciabole, ma gli esperti mi scusino) sono il vettore v e il vettore u. Esse, in generale, fanno un angolo tra di loro, che chiamiamo ϑ, come mostrato in Fig. 10. Non stupitevi se le due spade vanno nello stesso verso… pensatelo come una fuga di chi subisce il colpo. La spada v cerca di colpire e cala il suo fendente verso la spada u. Quali sono i fendenti dei vettori? Presto detto: le sue coordinate, ossia le proiezioni lungo degli assi particolari. In questo caso l’asse scelto non può che essere l’altra spada (u). Cosa fa quindi il nostro vettore v? Costruisce la sua componente scalare, ossia la proiezione del suo modulo, proprio lungo la direzione del vettore u. La chiamiamo v_u, ed essa è, ovviamente, uno scalare. Usa il modulo, perché è il modulo che indica la “grandezza” (la violenza, in poche parole) per fare cadere brutalmente la componente sopra la direzione del vettore vittima.

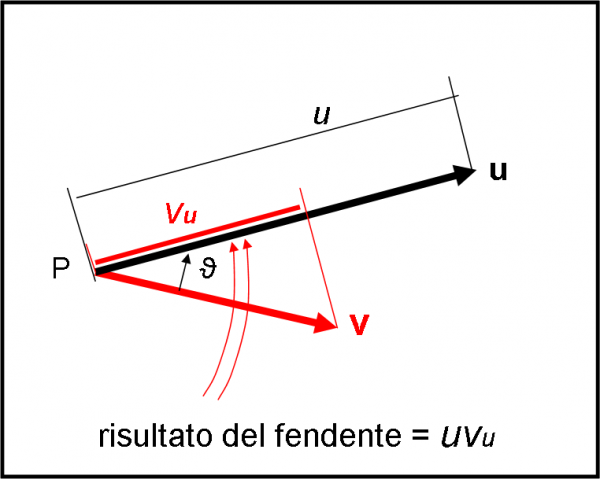
A questo punto v fa pesare la sua potenza d’azione, che viene quantificata dal prodotto (normale) tra la sua componente (il fendente) e il modulo u del vettore che ha subito il colpo. Insomma, in parole molto più serie: la sua componente moltiplicata per u. Per mantenere la nostra similitudine, potremmo dire che il fendente è quello che è, ma il risultato finale dipende da quanto è “grosso” l’avversario. Più è grosso e più il colpo è pesante e decisivo!

Forse qualcuno si sta stufando di questa trattazione puerile e fatta di ripetitive similitudini. Scusatemi, tra poco ripeterò le cose in modo più serioso. Il motivo è quello di cercare di offrivi un modo avventuroso e divertente per spiegare certi concetti ai più giovani, magari anche bambini. Non è mai troppo presto per capire cosa sono i vettori…

Possiamo definire l’azione che è stata svolta in un modo un po’ più fisico. Il vettore u ha una sua direzione e verso e quindi possiamo immaginarlo come un “trenino” che trasporta con sé il vettore v, attaccatogli in P. Tuttavia, siamo interessati solo alla parte del vettore v che si proietta sul treno u, ossia alla sua componente v_u. Più la componente è grande è più è grande il carico che mettiamo sul treno. Il risultato dell’azione svolta è il prodotto tra il modulo del … treno (u) e il carico parziale di v (la sua componente) inserito su di lui, v_u. Dato che uv_u è un prodotto normale tra scalari, potremmo anche dire che ci informa sulle condizioni finali del treno. Se  v_u fosse uguale a 1, avremmo il treno normale di partenza, ma dato che è stato moltiplicato brutalmente per un carico diverso da 1 (pari a v_u) il treno  deve faticare di più. Il risultato, comunque, è che il peso aggiunto comporta una fatica, un lavoro maggiore. Vedremo tra non molto quanto è azzeccata la parola lavoro.

Se queste parole in libertà vi hanno annoiato, dimenticatevele e riassumiamo “tecnicamente” cosa abbiamo fatto. Abbiamo costruito la componente v_u, del modulo v del vettore v, lungo la direzione di u e poi l’abbiamo moltiplicata per il modulo u del vettore u. Ossia, in termini matematici, il prodotto scalare dei due vettori v e u non è altro che la moltiplicazione delle due grandezze scalari v_u e u.

Abbiamo già capito perché si chiama prodotto scalare di due vettori: si parte da due vettori e si arriva a moltiplicare due scalari, il cui risultato è ancora uno scalare, ovviamente. Prima di scrivere per bene la formula che lo definisce, dobbiamo decidere che simbolo dare al prodotto scalare. Vi sono varie possibilità, basta mettersi d’accordo. Io preferisco rifarmi ai “miei” tempi e uso il simbolo x (il simbolo “antico” della moltiplicazione tra scalari), ma su internet e nei libri troverete anche altre simbologie. La formula che definisce il prodotto scalare (ossia il fendente tra due spade inclinate di un certo angolo tra loro) è, quindi, veramente semplice:

v x u = v_uu  … (8)        come già avevamo abbondantemente anticipato

Innanzitutto, troviamo quello che abbiamo detto fin dall’inizio: il prodotto scalare di due vettori è uno scalare ed è dato dal prodotto tra il modulo della componente del primo vettore, lungo la direzione del secondo, e il modulo del secondo.

Se vi sono sembrato troppo semplice, potrei velocemente complicare le cose e dirvi che il prodotto scalare è una trasformazione che associa a due elementi di un campo vettoriale un elemento di un campo scalare… Parole, parole, che noi possiamo benissimo tralasciare, ma non ci può sfuggire il fatto che usare il significato matematico più generale ci permetterebbe di entrare nelle teorie dei campi … ecc., ecc.

Torniamo alle nostre spade e cerchiamo di scrivere meglio la (8). Meglio abbondare e disegniamo la Fig. 11 che differisce ben poco rispetto alla Fig. 10.

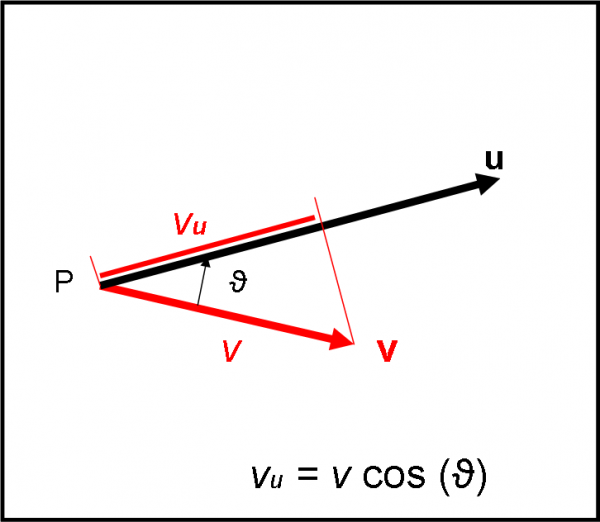
Siamo o non siamo in grado scrivere un po’ meglio la componente v_u? Direi proprio di sì, l’abbiano già fatto varie volte. In fondo, conosciamo l’angolo tra le due spade e quindi… basta usare quel poco di trigonometria che conosciamo:

v_u = v cos (ϑ)

e, quindi:

v x u = vu cos (ϑ)    …. (9)

In poche parole, il prodotto scalare di due vettori è il prodotto dei loro moduli moltiplicato per il coseno dell’angolo compreso.

Non sempre il fendente riesce

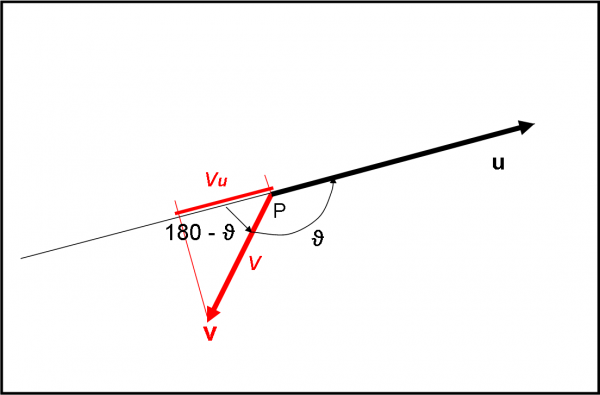
Continuiamo con la similitudine spadaccina… Se il vettore v sbaglia completamente il fendente e lo esegue nel verso opposto (Fig. 12) il risultato sarà un risultato davvero “negativo”. Infatti la sua componente v_u è relativa a un vettore v che va in verso opposto rispetto a u e quindi  l’angolo ϑ è ottuso. Ricordando che

cos (180 – ϑ) = - cos (ϑ)

il prodotto scalare risulta negativo. La formula da applicare è, comunque, sempre la stessa: ci pensa il coseno a darci il segno giusto.

Non ci credete? Proviamo con un esempio .

ϑ = 60° ,   v = 2 ,    u = 5

v x u = vu cos (60°) = 2･ 5 ･ 0.5 = 5

ϑ = 120°,  v = 2 ,    u = 5

v x u = vu cos (120°) = vu cos (180°- 60°) =  - vu cos (60°) = - 2･ 5 ･ 0.5 = - 5

Per riallacciarci al caso del treno, potremmo dire che il carico non ben sistemato tende a far rallentare il treno e prima o poi cadrà. Tutta fatica inutile, un lavoro veramente negativo!

Ognuno può tirare il fendente

Il prodotto scalare è un’azione di scherma che non ha favoriti ed è del tutto reversibile. In altre parole, il risultato non cambia se l’azione viene svolta da u a scapito di v. Lo vediamo nella Fig. 13.

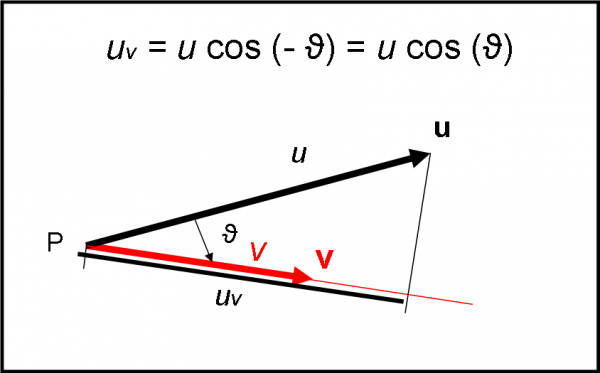
Possiamo benissimo costruire la componente di u lungo la direzione di v (è u che porta il fendente)  e calcolare il nuovo prodotto scalare, tenendo presente che l’angolo tra di loro rimane lo stesso, ma cambia di segno (ossia diventa – ϑ). Si ottiene:

u x v = u_vv = uv cos (- ϑ) = uv cos (ϑ)

Dobbiamo infatti ricordare che cos (- ϑ) = cos (ϑ).

Un risultato molto importante, dato che ci permette di scrivere:

u x v = v x u

Vale, perciò, la proprietà commutativa. Non è cosa tanto ovvia e banale, dato che il prossimo prodotto si comporterà in modo ben diverso… In termini schermistici, qualsiasi  dei due vettori tiri il fendente il risultato è esattamente lo stesso.

Sì, lo so, l’ho fatta lunga, ma penso che i vettori meritino un trattamento di favore. Il prodotto scalare non si troverà molto spesso in fisica, ma sicuramente è fondamentale quando si definisce il lavoro di una forza. Anzi, il lavoro è proprio il prodotto scalare di due vettori: la forza che agisce su un punto (o un corpo) e lo spostamento del punto (o del corpo). Pensateci e, prima o poi, ne parleremo.

Spade incrociate o allineate

Mi soffermo, invece, ancora un po’ sull’utilità del prodotto scalare nel definire la direzione reciproca di due vettori. Riscriviamo il nostro prodotto :

v x u = vu cos (ϑ)

Quando questo prodotto diventa uguale a zero? Beh, ci sono solo tre modi per ottenerlo: o va a zero il primo vettore o va a zero il secondo vettore oppure va a zero il coseno. Ovviamente, noi consideriamo vettori non nulli (che spade sarebbero?) e non ci rimane che porre il coseno uguale a zero.

Ma, per quali angoli va a zero il coseno? Presto detto solo per 90° o 270°, ossia per vettori perpendicolari tra loro (a parte il verso). Quindi, possiamo dire che due vettori sono perpendicolari solo e soltanto se il loro prodotto scalare è uguale a zero. E’ vero anche il viceversa, ma spesso si usa il prodotto scalare proprio per risalire alla direzione dei vettori.

Cosa succede, invece, se i due vettori sono paralleli tra loro? Beh… l’angolo diventa 0° (o 180°) e il coseno proprio 1  (o -1). Il prodotto diventa un valore massimo (o minimo) uguale al prodotto dei moduli (uv).

Se, inoltre, i due vettori fossero proprio uguali tra loro (stessa direzione, stesso verso e stesso modulo), l’ultimo caso darebbe proprio il quadrato del modulo del vettore (vu = vv = v²). In parole schermistiche: se le spade restano perpendicolari vi è un nulla di fatto; se una spada va completamente lungo la direzione dell’avversario si ottiene una poderosa botta dritta.

Versori e componenti lungo gli assi cartesiani

L’utilizzo di vettori uguali tra loro, ci fa tornare in mente i versori i e j. Per “piccoli” che siano sono pur sempre vettori! Sapreste dirmi quanto valgono i loro prodotti scalari, ossia:

i x j =

j x j =

i x i =

j x j =

Pensateci un attimo, prima di proseguire… dato che ho bisogno del risultato per la parte successiva. Avete risposto? Bene… allora sapete che

i x j = j x i = 0

i x i = j x j = 1

A questo punto inserisco la parte più “complicata”, che potete anche saltare, ma che è giusto inserire per gentilezza verso i nostri amici versori. In altre parole, vogliamo calcolare il prodotto scalare di due vettori, attraverso le loro componenti lungo i due assi cartesiani x e y. Dobbiamo farci, ovviamente, aiutare dai due versori degli assi cartesiani, i e j.

Come sappiamo dalla volta scorsa , possiamo scrivere il vettore v come

v = v_x i + v_y j

e quello u come:

u = u_x i + u_y j

Il prodotto scalare diventa:

v x u = (v_x i + v_y j) x (u_x i + u_y j) = v_xu_x i x i + v_x u_y i x j + v_y u_x j x i + v_y u_y j x j         …. (10)

Tuttavia, sappiamo che:

i x i = 1

i x j = 0

j x i = 0

j x j = 1

Basta sostituire e la (10) diventa:

v x u = v_xu_x + v_y u_y    …. (11)

in altre parole: il prodotto scalare di due vettori è dato dalla somma dei prodotti (normali…) tra le rispettive componenti (scalari) sugli assi cartesiani.

Evviva lo spazio

Prima di fare il passo successivo (sicuramente un po’ più impegnativo), lascatemi introdurre la terza dimensione, ossia l’asse z, perpendicolare al piano xy. Purtroppo, il prossimo prodotto, benché eseguito su un piano, ha bisogno della terza dimensione… Tanto vale allora, utilizzarla già adesso e riscrivere la relazione (10) nello spazio a tre dimensioni, dove un vettore ha ora tre coordinate: v_x, v_y e v_z. Essa diventa (non è certo difficile ottenerla):

u x v = v_xu_x + v_y u_y+ v_z u_z   …. (12)

Non sto a fare i conti completi, basta solo ricordare che, se k è il versore relativo all’asse z, avremo:

i x k = 0

j x k = 0

k x k = 1

Dato che l’asse z è perpendicolare sia all’asse x che all’asse y.

Bene, scusate le digressioni sulla scherma e poi gli affondi più impegnativi. Ho cercato di eseguire una trattazione che vada bene un po’ per tutti, dai neofiti ai più esperti. Ognuno, a modo suo, dovrebbe avere compreso il significato di prodotto scalare di vettori.

Non ci resta, adesso, che passare alla “presa di ferro” o a qualcosa di simile…