Dopo i consigli baricentrici per una sana alimentazione anche a Natale, non potevano mancare i consigli per trascorrere un Santo Stefano in perfetto stile Art-Attack. E poi non dite che non pensiamo a voi, cari lettori.

Buon divertimento a grandi e piccini di tutte le età!

 

(Scritto per i bambini ma utile anche ai genitori)

Con due triangoli equilateri di cartone e una puntina da disegno possiamo verificare il calcolo dello spostamento del baricentro di un sistema quando aggiungiamo qualche nuovo elemento.

Innanzitutto prendiamo una scatola di cartone (ne avrete la casa piena con tutti i regali di Natale che avrete ricevuto) e ricaviamone due triangoli equilateri. La costruzione con riga e compasso è semplicissima: uno lo vedete con la punta in su e l'altro potete tracciarlo sotto con la punta in giù.

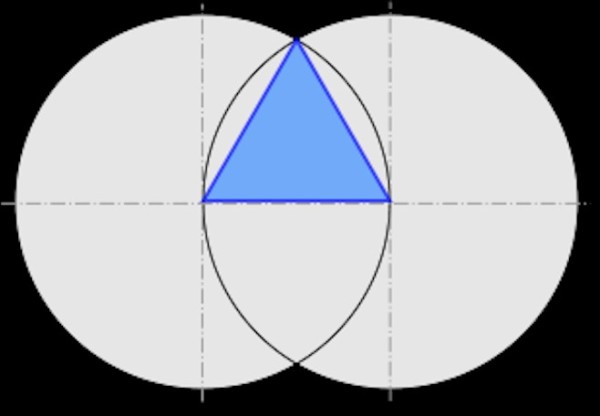
Ritagliate ( o fatevi ritagliare) i due triangoli. Ora che avete questi due triangoli tracciate le mediane di due dei loro lati e trovate il loro baricentro:

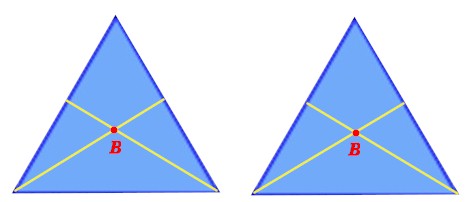
Non vi resta che aspettare che il genitore meno scientifico si allontani e, con l'aiuto dell'altro, eseguite questa interessante sperimentazione.

Prendete la puntina. Se pensate che non sia il caso di fare buchi nella porta di legno della cucina, potete appoggiare un magnetino alla porta del frigorifero e fargli attrarre la puntina da disegno in modo che la punta sia rivolta all'esterno.

A questa punta appenderete uno dei due triangoli, facendo un buchino in un vertice, così

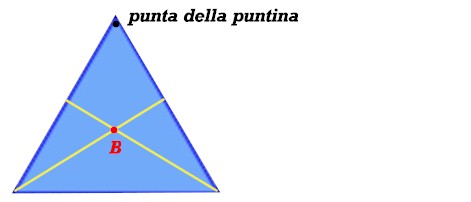
Naturalmente, data la simmetria del triangolo, il baricentro sarà allineato con la verticale e la base risulterà perfettamente orizzontale.

Adesso è il momento di aggiungere il secondo triangolo. Lo fisseremo con una goccia di colla piazzata sul suo baricentro, al vertice destro della base del primo triangolo.

Facendo questo aggiungiamo al peso del primo triangolo ( concentrato nel suo baricentro) un peso identico concentrato in questo vertice .

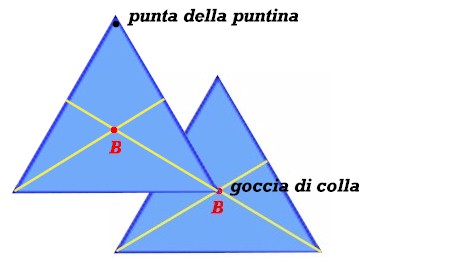
Nei due baricentri si concentrano i due pesi (uguali) dei triangoli. Il NUOVO baricentro si troverà a metà strada sulla congiungente dei due punti B.

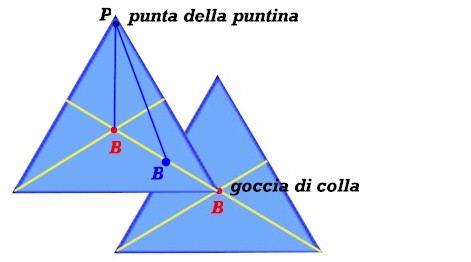
Eccolo lì, scritto in blu: in esso si concentra la somma dei due pesi. Però notiamo che il nuovo baricentro non si trova più sulla verticale passante per il punto di sospensione P. Tra il vecchio e il nuovo baricentro si è formato l'angolo BPB.

Le cose non possono ovviamente rimanere in questo stato che non è stabile.

Quello che vediamo è l'istante di inizio di un movimento di rotazione attorno a P , grazie al quale il nuovo baricentro si sposterà nel punto più basso consentitogli, allineandosi in verticale con il punto di sospensione.

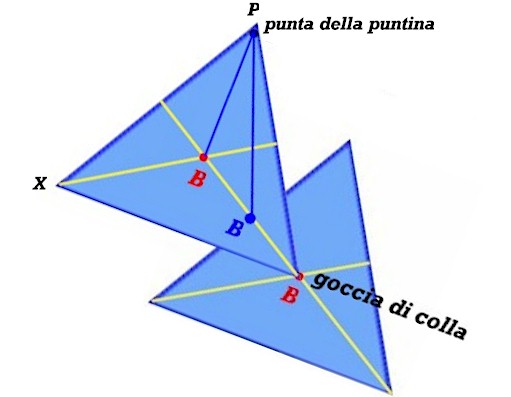
Mentre il baricentro blu si porta sotto la puntina P, il vertice sinistro del primo triangolo si solleva fino al punto X. Non è difficile capire che l'angolo tra il lato BX e l'orizzontale è lo stesso trovato prima, ossia BPB. Tutto quanto ha subito la medesima rotazione.

A questo punto ci troviamo tra le mani una specie di bilancia “equilatera”.

Infatti, se stacchiamo delicatamente il secondo triangolo, lo dividiamo in 4 parti uguali, così:

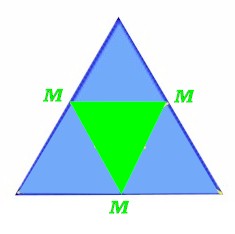
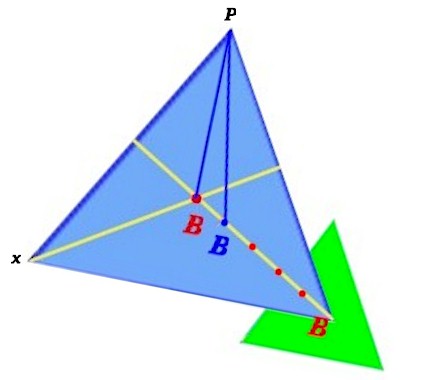
ossia congiungendo i punti medi M dei tre lati, prendiamo uno dei quattro triangolini, ad esempio quello verde, e lo andiamo appiccicare per il suo baricentro al solito vertice di prima, vedremo che si verificherà una rotazione più modesta di prima e potremo prevedere dove si posizionerà questa volta il vertice sinistro.

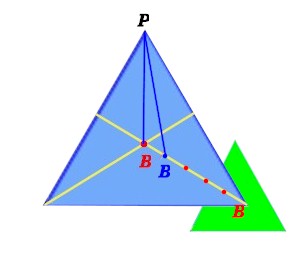
Ricordate che questa volta i pesi dei due triangoli non sono uguali: quello verde pesa un quarto di quello azzurro.

Per questo motivo, invece di cadere nel punto intermedio, il nuovo baricentro viene attratto “quattro volte di più ” da quello maggiore, e gli va vicino in questa proporzione, come si vede nella figura sopra. La distanza tra i due baricentri è divisa in 5 tratti: uno solo separa il baricentro maggiore dal nuovo baricentro blu, mentre gli altri quattro tratti lo separano dal baricentro minore. Non è altro che la legge dell'equilibrio di una leva con il punto di appoggio intermedio, una leva cosiddetta di primo genere.

E' intuitivo l'angolo di deviazione del baricentro è più piccolo di prima e la rotazione che avrà luogo porterà il vertice sinistro in una posizione, che indicheremo con “x” minuscola, più vicina alla linea orizzontale.

Potremo ripetere più volte l'esperimento sovrapponendo con precisione due , e poi tre di questi triangoli piccoli, ottenendo sempre posizioni diverse e prevedibili di “x”.

Per ciascun peso applicato, la posizione di x cambia e, nell'insieme, tutte queste posizioni costituiscono la scala di lettura della nostra bilancia, in cui ciascuna divisione è relativa ad una frazione del peso del triangolo equilatero ( un quarto, un mezzo , tre quarti,  etc.).

Saremo sempre in grado di dire che il peso incognito è compreso tra le indicazioni di due divisioni contigue.

Quello che abbiamo visto è il comportamento statico del sistema, tra due posizioni di equilibrio iniziale e finale.

Noterete che nella realtà, prima di raggiungere l'equilibrio, la bilancia compie delle oscillazioni. Essa, a tutti gli effetti, costituisce un pendolo. Queste oscillazioni hanno una ampiezza che si va smorzando per via degli attriti ed un periodo che è determinabile a priori, conoscendo la forma e le dimensioni del sistema. Ma questo è un discorso che faremo, magari, in un' altra occasione.

Adesso la cosa più importante è mettere tutto a posto, togliere la puntina, il magnete e allontanarsi con indifferenza dal frigorifero, prima che torni il genitore ascientifico e abbia qualcosa da ridire.

Auguri !