La soluzione del QUIZ è probabilmente più facile di quello che poteva sembrare a prima vista. Maurizio è riuscito ad arrivare al dunque (dovrebbe passare un mesetto a casa dei pappidi che ama veramente tanto). Tuttavia, io presento un’altra soluzione (ben poco diversa) che fa uso di un teorema di Euclide tra quelli meno noti…

Prima di dare la soluzione “euclidea” devo ricordare, perciò, un teorema che deriva proprio dai calcoli stupefacenti del grande greco: il teorema delle corde. Può essere enunciato in vari modi, ma noi usiamo quello che ci porta velocemente al nostro quiz: “Considerate due corde qualsiasi (non parallele) di uno stesso cerchio, esse si intersecano in un punto che divide le corde in due segmenti. Il prodotto tra i due segmenti della prima corda è uguale al prodotto dei segmenti dell’altra corda".

Vediamolo, insieme alla banale dimostrazione, in Fig. 1

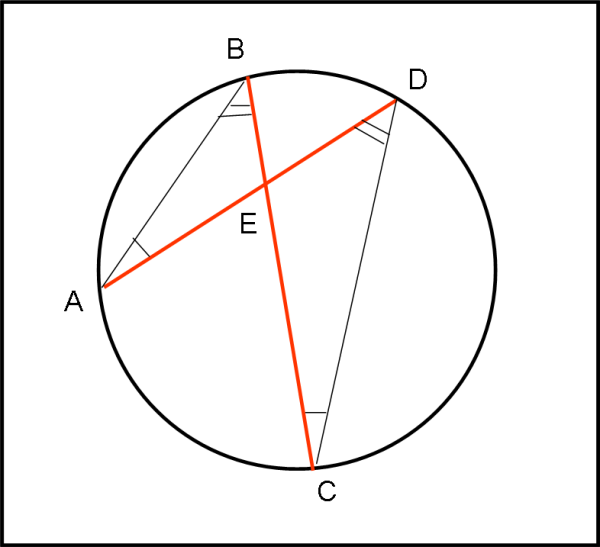
Le due corde sono AD e BC, dobbiamo dimostrare che

ED·AE = BE·EC

La relazione si ottiene subito considerando i due triangoli AEB e DEC. Essi sono simili aventi tutti e tre (ne bastavano due) angoli uguali. Quelli in E perché opposti al vertice; quelli in A e in C perché angoli alla circonferenza dell’arco BD ; quelli in D e B perché angoli alla circonferenza dell’arco  AC.

Ne segue:

ED/BE = EC/AE

e, quindi:

ED·AE = BE·EC

Applichiamo il teorema alla nostra avventura, dove le due corde sono scelte in modo da essere perpendicolari tra loro,come mostra la Fig 2. Esse sono BF e CE.

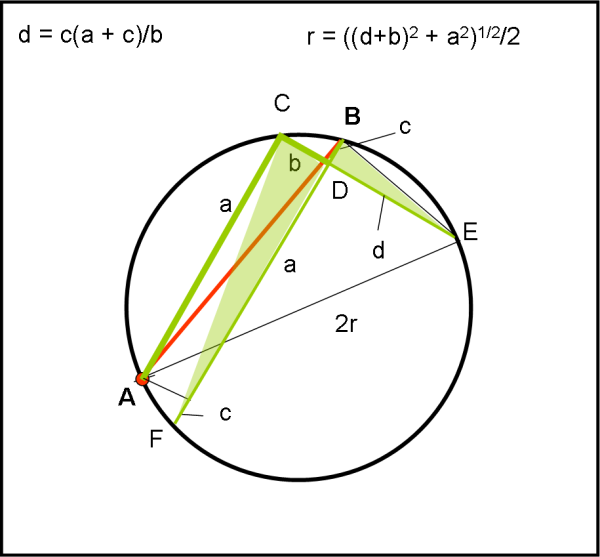
Senza esagerare, poniamo il primo tracciato AC abbastanza vicino alla direzione AB. Notiamo che AC può comunque essere qualsiasi. Poi giriamo di 90° e ci dirigiamo verso E, stando bene attenti (per mezzo della squadretta e del regolo) di fermarsi quando si arriva al punto D da cui si può raggiungere B ruotando di 90°. Tutto ciò risulta “tecnicamente” fattibile solo se il punto C è molto vicino a B (che è proprio quello che vogliamo).

Chiamiamo i vari segmenti del tracciato di Pappo con lettere minuscole per maggiore comodità nella parte finale (terza domanda). Il tracciato da seguire è ACDE. Si vede subito che più C si avvicina a B e più il tracciato tende alla minima distanza tra A e B (seconda domanda).

AB = a

CD = b

DB = c

DE = d

Ovviamente i primi tre sono noti e basta poco per ricavare d, applicando il teorema delle corde alle due corde perpendicolari BF e CE, che si intersecano in D.  Possiamo scrivere:

FD·DB = DE·CD

Ma FD non è altro che (a+c)

Per cui si ottiene:

(a + c)c = bd

d = (a + c)c/b              …. (1)

d si calcola facilmente per mezzo dei tre segmenti misurati direttamente da Pappo.

Adesso non resta che considerare il triangolo rettangolo ACE (l’angolo in C è per costruzione retto e quindi la corda AE deve essere un diametro, ossia AE = 2r

Basta applicare il teorema di Pitagora e si ottiene:

4r² = (d + b)² +  a²        …. (2)

Avremmo risposto a tutte le domande, ma, per accontentare i matematici (e fare un po’ di esercizio), proviamo a scrivere nel modo più compatto possibile la relazione tra r e i tre tratti effettivamente percorsi da Pappo, ossia a, b e c. Non ci resta quindi che inserire il valore di d, in funzione di a, b e c, come indica la (1).

4r² = a² + ((a + c)c/b + b)²

4r² = a²b²/b² + (((a + c)c + b²)/b )²

4r² = a²b²/b² + ((a + c)c + b²)²/b²

4r² = a²b² + (ac + c² + b²)²/b²

Scriviamo 2b²c²  come  b²c² + b²c² e facciamo un po’ d’ordine al numeratore. Poi estraiamo la parte segnata in rosso

4r² = (a²b² + b⁴ + 2 acb² + c²b² + a²c² + c²b² + 2ac³ + c⁴)/b²     …. (3)

E la scriviamo mettendo in evidenza b²:

b²(a² + b² + 2ac + c²) = b²(b² + (a +c)²)

Facciamo lo stesso con la parte in blu, mettendo in evidenza c²

c²(a² + b² + 2ac + c²) = c²(b² + (a + c)²)

Per cui la (3) può scriversi:

4r² = (b² + c²)( b² + (a + c)²)

r = ((b² + c²)( b² + (a + c)²))^1/2/ 2b

Magari si può fare anche di meglio, ma, se non altro, ci siamo divertiti con un po’ di passaggi matematici.

Notiamo che il risultato è esattamente lo stesso trovato da Maurizio e inserito nei commenti. Il suo metodo è –probabilmente- ancora più rapido. In ogni modo quello riportato in questa soluzione ci ha permesso di richiamare uno dei tanti teoremi di Euclide.

Penso, infine, che basti l’occhio e il ragionamento (ma si può anche rendere matematicamente e/o geometricamente ineccepibile) per concludere che il limite della linea spezzata è proprio la corda AB…

Viva Euclide, ma bravi anche i nostri maghi!