Un mio semplice articolo di tanti anni fa, che può diventare un gioco per tutti e che dà luogo a "stelle" veramente fantastiche, malgrado si parli di asteroidi…

Abbiamo già parlato di come attraverso la curva di luce si possa avere un’idea della forma di un asteroide (QUI). Ovviamente se l’asteroide è sferico o viene visto proprio nella direzione dell’asse di rotazione (come Ultima Thule), la curva di luce è fondamentalmente piatta, dato che gli asteroidi devono la loro variazione di luminosità essenzialmente alla variazione dell’area apparente che mostrano all’osservatore.

In realtà, variazioni di luminosità possono anche derivare da differenze di albedo sulla superficie, ma si è visto che generalmente questa possibilità è decisamente meno importante dell’effetto puramente geometrico. L’unico caso macroscopico in cui chi comanda la curva di luce è una macchia di albedo è quello di Vesta, uno sferoide che ha quasi un intero emisfero profondamente segnato da un enorme cratere da impatto (proprio quello da cui è nata la sua famiglia).

Eravamo alla fine degli anni ’70 e per determinare il periodo di rotazione e iniziare ad accumulare dati per determinare la direzione dell’asse di rotazione la norma era quella di considerare la forma generica assimilabile con un ellissoide a tre assi, facilmente trattabile analiticamente. Ne abbiamo parlato a lungo QUI. Bisognava anche tener conto dell’angolo di fase solare che sicuramente influiva sull’andamento della curva di luce quando le ombre delle irregolarità superficiali si allungavano e coprivano zone piuttosto vaste della superficie teoricamente in luce.

Insomma, non era così banale nemmeno ricavare il periodo di rotazione che, teoricamente, doveva essere rappresentato da due massimi e due minimi per ciclo. In media per oggetti molto allungati questo andamento era seguito abbastanza bene, anche se l’altezza dei due massimi e dei due minimi spesso e volentieri non si ripeteva esattamente tra un emisfero e l’altro. Comunque, bastava ipotizzare qualche craterone o montagna o una spruzzata di albedo più o meno scura per accettare come periodo quello classico.

Ben diversa era la situazione per oggetti più vicini a una sfera, dove anche piccole variazioni topografiche o di albedo potevano competere con le variazioni di area apparente. I massimi e minimi venivano comunque cercati con attenzione e osservazioni in giorni diversi trovavano la loro sovrapposizione ideale quando la curva finale si avvicinava a quella “teorica”.

Cominciò a farsi strada l’idea degli asteroidi doppi (vi era stata un’occultazione di Herculina che aveva fatto pensare a un satellite,  poi tutto era rientrato). Devo ammettere che fui uno dei primi ad analizzare gli effetti geometrici e i giochi di ombra che potevano dare un segnale abbastanza peculiare per pensare alla binarietà. Insieme ai colleghi di Pisa scrivemmo i primi articoli sia osservativi che teorici su questa possibilità che sembrava ai più una forzatura poco plausibile (oggi le cose sono molto cambiate…). Penso che valga la pena richiamare quegli articoli e farne una breve sintesi: in fondo sono stati i primi ad alzare il dito verso lo sdoppiamento di quei piccoli oggetti che stanno guadagnando sempre più posizioni nell’interesse astrofisico. Vi prometto che lo farò quanto prima.

Mentre ormai cercavamo di vedere tutto doppio (grandi bevute di buon vino?), il fatto di essere all’inizio di un tipo di ricerca del tutto nuova (gli asteroidi erano considerati punti di luce utili solo per determinarne le orbite) causava spesso che anche le cose più banali potevano essere trascurate e le galline non faticavano a regalare tante uova di Colombo.

Non solo si doveva guardare con estrema attenzione ai piccoli segnali legati alla duplicità, ma anche a cose ben più macroscopiche.  Studiando le curve di luce che si moltiplicavano in fretta si notava sempre più che i due massimi e i due minimi non erano così chiari e non era facile capire quando la rotazione era veramente stata completata (a volte vi era il dubbio che qualche picco fosse da considerare come massimo secondario o solo una variazione di luce dovuta  a un’imponente irregolarità superficiale).

In parole povere, pensai alla possibilità di forme ben lontane dall’ellissoide a tre assi. Non era nemmeno necessario impostare programmi di modellizzazione (a quei tempi non facili visto il livello dei computer). Non è che, per caso, esse dessero una curva di luce con un numero maggiore o minore di massimi e minimi (chiamiamoli anche estremi), durante l’intera rotazione?

Una forma geometricamente strana poteva mascherare e moltiplicare il numero di estremi per ciclo e magari dare risposte a curve di luce troppo irregolari per scaricare tutto su una montagna o un macchia.

Oggi sembrerebbe una dubbio da povero sprovveduto ma, allora, non era ancora stato affrontato da nessuno. Perché non provare, partendo dai casi più semplici e estremamente semplificabili? Qualcosa che poteva essere fatto senza tanti modelli, ma solo con un minimo di trigonometria, una calcolatrice tascabile, un foglio di carta millimetrata e… tanta voglia di giocare.

In qualche modo era l’inizio, di una semplicità mostruosa, che avrebbe poi portato a modelli sempre più sofisticati e alla risoluzione (sempre un po’ ambigua) dell’inversione di una curva di luce. Oggi è un problema più che gestibile e lo dimostra anche il nostro amico Lorenzo Franco. Nel modello poteva poi essere aggiunta la fase, le piccole irregolarità superficiali, la craterizzazione e molte altre cose più sofisticate. Poi vennero le immagini prese in diretta dalle missioni spaziali che, in fondo, confermarono il grande lavoro teorico basato solo sulla curve di luce  (Vesta insegna… il nostro modello era praticamente uguale alle immagini ottenute da Hubble prima e da Dawn dopo).

Visto che trattiamo spesso la storia antica e i suoi grandi geni senza tempo, permettetemi di richiamare in modo sintetico il mio lavoro del 1980, una piccola cosa, non certo geniale, alla portata di tutti, che però aprì una visione completamente diversa dell’informazione data dalle curve di luce. Ho quasi vergogna a parlarne oggi, ma ho molta nostalgia di quei tempi veramente pionieristici e non ho problemi a proporlo agli amici di questo circolo.

Le ipotesi di partenza sono veramente elementari. Invece di un ellissoide, proviamo a considerare forme geometriche molto più semplici e facilmente trattabili come un parallelepipedo,  una piramide,  una specie di cuneo (Pautasso stai tranquillo!) o un prisma triangolare. Un gioco da bambini, ma i risultati stupirono un po’ tutti… Che bambinoni eravamo… Riprendemmo il lavoro in modo molto più raffinato molti anni dopo (ho già messo il link all’articolo, ma risulta ancora a pagamento), ma le cose, in fondo, non cambiarono di molto…

Già il lavoro che pubblicai da solo (non volevo coinvolgere nessuno in quella specie di scherzo) era poco più che un gioco da bambini, ma lo avevo condito con qualche formuletta trigonometrica (roba da poco), per cui oggi voglio eliminare qualsiasi parte matematica e presentarlo proprio come un passatempo o poco più, ricco di tante bellissime stelline, non sempre facilissime da costruire (mettetevi alla prova): il massimo per un planetologo!

Iniziamo col richiamare quello che già sappiamo sulla rotazione di un ellissoide a tre assi, utilizzando una sola figura (Fig. 1) con i vari passi da eseguire.

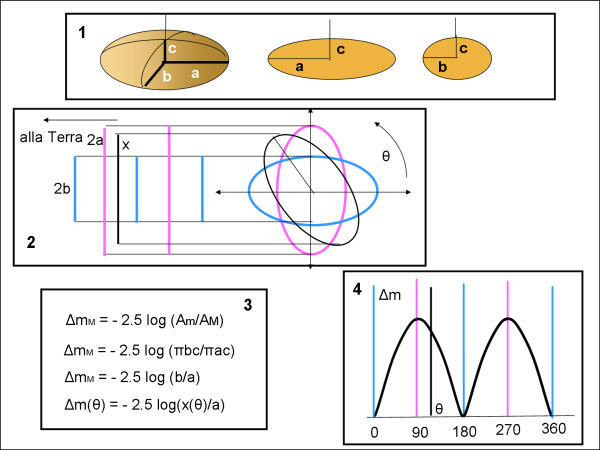
Nel riquadro (1) abbiamo il nostro ellissoide che ruota attorno al semiasse minore c (a > b > c). Per semplicità ci mettiamo proprio in una posizione “equatoriale”, ossia vediamo l’asteroide perpendicolarmente all’asse c. Ricordiamo che questa configurazione capita sempre per qualsiasi oggetto durante la sua rivoluzione attorno al Sole.

Nel riquadro (2) riportiamo proprio il piano equatoriale con l’osservatore a sinistra. E’ immediato comprendere che l’area dell’ellissoide visto dalla Terra  sarà data da πac, mentre quella minima (ottenuta dopo una rotazione dell’angolo θ di 180°) sarà πbc. E questo vale anche per qualsiasi visione intermedia del tipo πcx(θ).  In poche parole, ogni area possiede una costante πc, che ci permette di lavorare solo nel piano equatoriale e calcolare anche graficamente la proiezione x al variare dell’angolo θ. Noi siamo interessati al rapporto delle aree, dato che una curva di luce ci regala la quantità di luce proveniente dall’area apparente e per valutare la differenza in magnitudine Δm basta applicare una formula ben nota (è l’unica ve lo assicuro) come descritto nel riquadro (3).

Δm = -2.5 log A₁/A₂   (dove A₁ e A₂ sono le aree apparenti).

Nel nostro caso riferiamo tutte le differenze di magnitudini all’area massima (πac) in modo a avere differenze di magnitudini positive (ma si può scegliere quello che si vuole).

La differenza massima Δm_M viene fornita dal rapporto tra l’ara minima e quella massima, ossia:

Δm_M = -2.5 log πbc/πac = -2.5 log b/a (lo zero delle differenze di magnitudine diventa il massimo della curva di luce.

Per un certo angolo θ si avrà una differenza

Δm(θ) = - 2.5 log (x/2)/a.

Il riquadro (4) riporta la curva di luce (equatoriale) corrispondente, con i suoi  due perfetti massimi e minimi per ciclo.

Abbiamo, comunque, imparato che per disegnare la curva di luce basta determinare la lunghezza del segmento, proiettato perpendicolarmente alla direzione di vista dalla figura piana che ruota nel piano equatoriale (l’altezza è sempre c) e farne il rapporto con il segmento massimo.

A questo punto, possiamo abbandonare il nostro ellissoide e inventarci qualche solido più semplice e ben conosciuto. Cominciamo con il parallelepipedo…

Il mattone

Consideriamo la Fig. 2. In alto abbiamo il modello: un bel mattone!

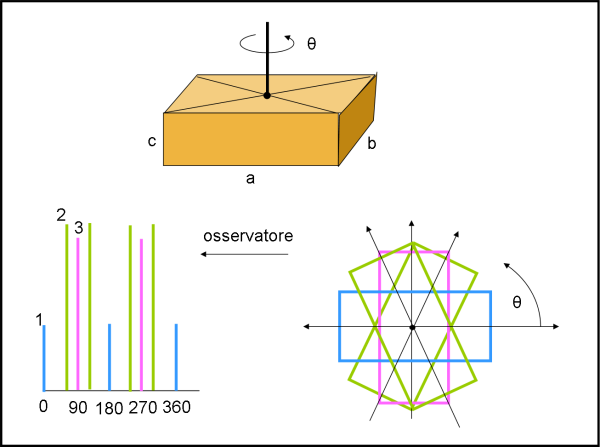
In basso a destra la nostra stellina-asteroide, che si costruisce facendo ruotare il rettangolo piano attorno al proprio baricentro. Non c'è bisogno di usare trigonometria...  Facciamolo partire nella posizione del rettangolo blu e segniamo a sinistra la lunghezza del segmento corrispondente alla sua proiezione nella direzione dell’osservatore. Il punto di partenza è il minimo, dato che si proietta solo il lato minore del rettangolo. Il secondo angolo fondamentale corrisponde al rettangolo verde (la proiezione è la diagonale del rettangolo, sicuramente il massimo). Poi, subito dopo, abbiamo un nuovo minimo relativo, ossia quando si proietta il lato maggiore a (rettangolo viola). A questo punto le configurazioni si ripetono.

Basta vedere l’andamento dei segmenti proiettati (a sinistra) per capire come sarà la curva di luce finale. Abbiamo un bel minimo profondo poi si arriva al massimo, seguito, però, da un minimo relativo che torna a un massimo prima di cadere verso un nuovo grande minimo, quando l’angolo è 180° (mezzo periodo). Per valori di a/b piuttosto alti (tipo a/b = 2) i due massimi e due minimi per ciclo sono ancora evidenti, ma quella piccola ondulazione del massimo è piuttosto interessante…

Non solo, però… quando il rapporto a/b diminuisce l’ondulazione del massimo diventa sempre più importante e potrebbe benissimo essere scambiata per un minimo vero e proprio, il che comporterebbe di dedurre un periodo che è solo la metà di quello vero. La faccenda diventa ancora più interessante per a/b = 1.

Ad esempio un vero e proprio cubo, come mostra la Fig. 3, che usa lo stesso schema di quella precedente.La stellina è decisamente banale, ma estremamente “cattiva”. I due massimi e i due minimi, perfettamente uguali rispettivamente, compiono il loro doppio ciclo esattamente in 180°. Il periodo sarebbe sicuramente dimezzato rispetto a quello vero!

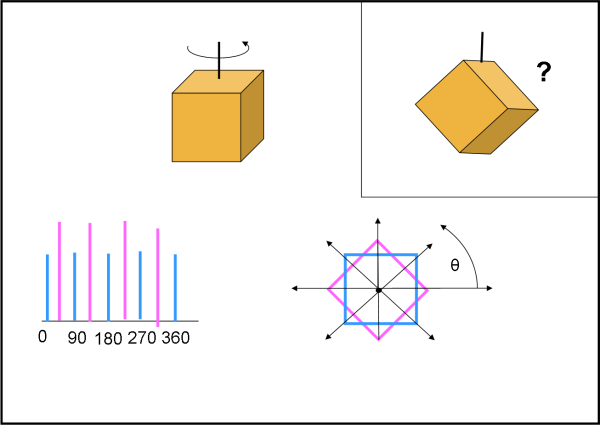
Qualcuno riderà, ma… ricordiamoci Ryugu (Hayabusa 2) e Bennu (OSIRIS-REx), due cubi o giù di lì… anche se ruotano attorno all’asse più lungo (meglio dire due tetraedri appiccicati). A destra in alto, ho solo preso il cubo e l’ho fatto girare secondo un asse parallelo alla diagonale… divertitevi pure a vedere che curva di luce viene fuori…

Noi, intanto, in Fig. 4 riportiamo le curve di luce complete per tre mattoni particolari (a/b = 2, a/b= 1.5 e a/b = 1 (il cubo)).

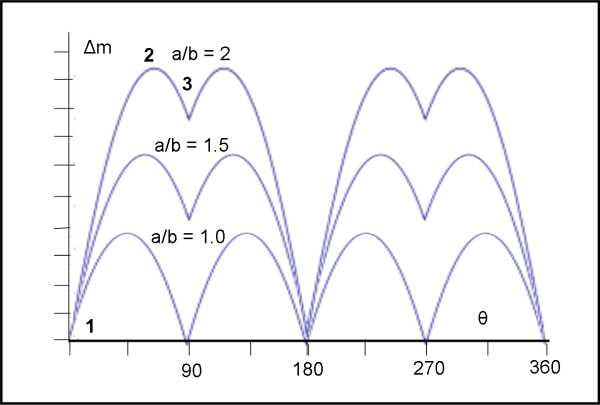
Ma, è il caso di andare a vedere se un’ipotesi così semplicistica avesse una ragione d’essere sollevata… Beh, basterebbe solo l’asteroide 49 Pales (Fig. 5).

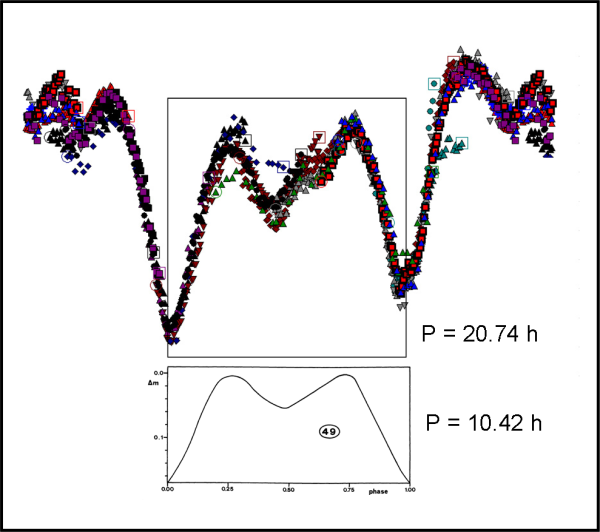
Osservato a una certa opposizione  avevamo dedotto un periodo di 10.42 ore. In seguito (magari anche grazie al mio lavoretto) si è determinato che il vero periodo era di 20.74 ore. Insomma, Pales è quasi sicuramente un bel mattone! E chissà quanti cubi continuano ad avere il proprio periodo dimezzato… Girando sul web troverete facilmente molti altri esempi.

Il prisma triangolare

E se invece di un mattone usassimo una specie di cuneo (un prisma triangolare per essere più esatti…)? Beh i risultati non sono niente male.

Iniziamo con il caso più emblematico: un triangolo equilatero… beh, proprio lui dà un risultato inaspettato. Ha una perfetta alternanza di massimi e minimi uguali, ma sembrerebbe completare il suo periodo in 120°. In altra parole, ciò che sembra il periodo  è solo un terzo di quello vero che ha ben sei massimi e sei minimi (Fig. 6).

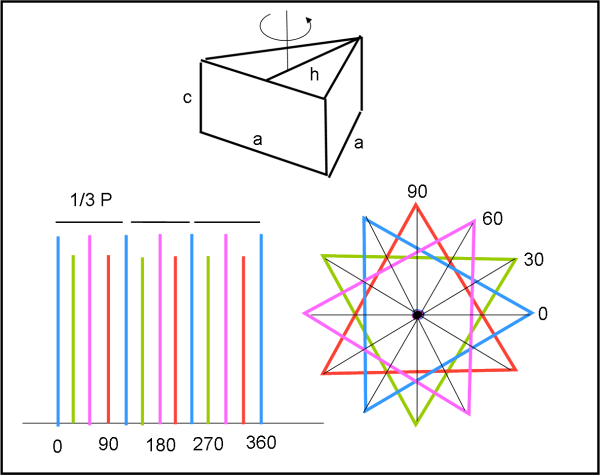
E che dire della forma stranissima che deriva da un triangolo isoscele con un angolo α di 90°? Il periodo è quello giusto, ma che andamento bislacco… (Fig. 7)

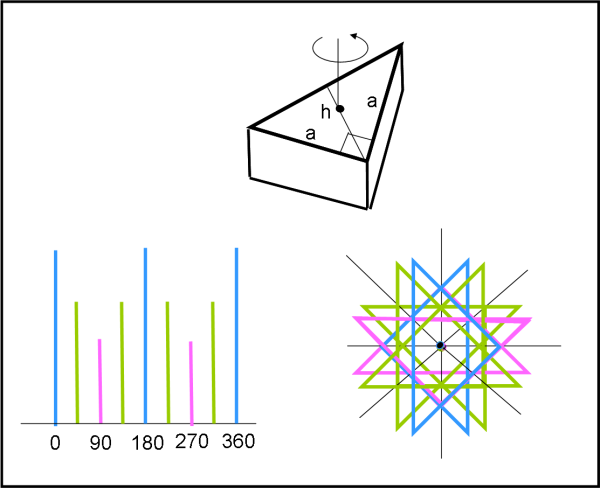
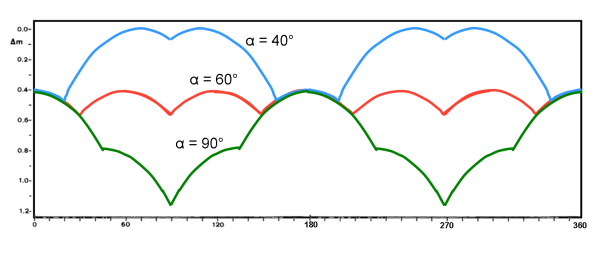
Se, invece, l’angolo α tra i lati uguali è acuto viene qualcosa di simile al mattone, ma con un minimo lungo e praticamente piatto. Tuttavia, dà luogo a una stellina durante la sua rotazione (Fig. 8 ) che è veramente fantastica  (in cui è difficile  districarsi…)

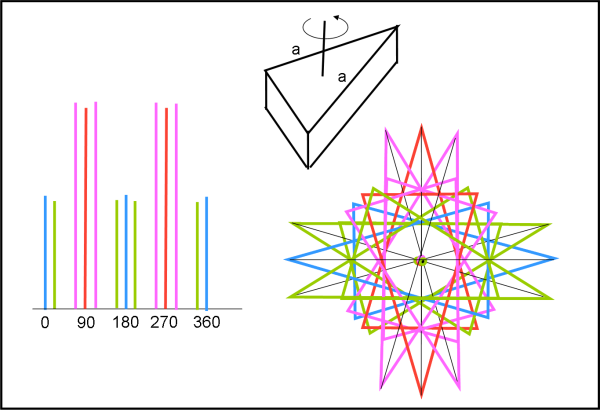
Qualche curva di luce è riportata in Fig.9

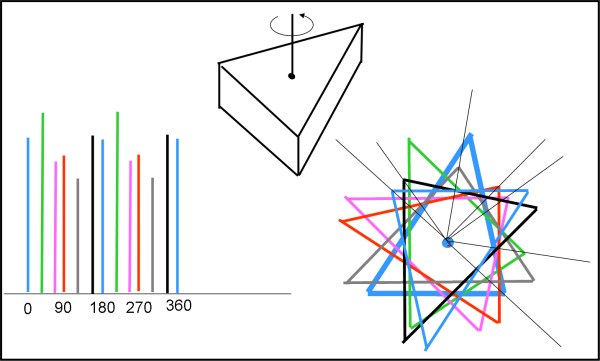
Ma le cose diventano ancora più interessanti, utilizzando un triangolo non isoscele. Si perdono molte simmetrie e si arriva a una rotazioni meno simmetrica, come in Fig.  10, dove per non complicare troppo ho ruotato il triangolo attorno al suo baricentro di soli 180°. Per ottenere la curva completa basta ripetere il risultato dei primi 180°.

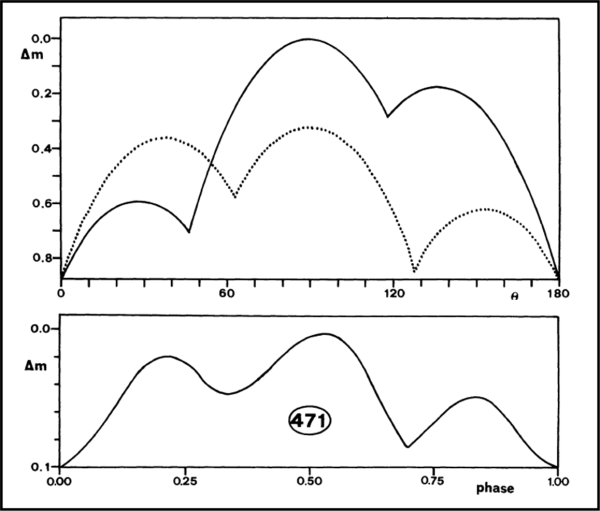
Guardiamo in Fig. 11 cosa viene fuori in due casi particolarmente interessanti, soprattutto quello tratteggiato. In entrambi i casi si hanno tre massimi e tre minimi durante una rotazione di soli 180°. Per confronto riportiamo la curva di luce dell’asteroide 471 Papagena e non possiamo che stupirci della somiglianza. Il periodo di Papagena era stato calcolato in 7.11 ore, ma se fosse veramente un po’ triangolare si dovrebbe raddoppiarne il periodo.

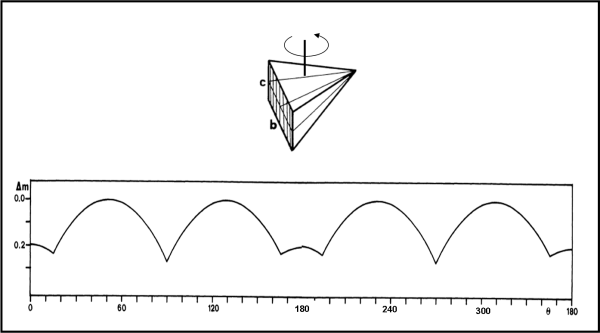
Concludiamo questa carrellata molto arcaica, ma abbastanza divertente (spero), considerando un unico caso della piramide a base rettangolare. Bene, per un angolo al vertice di 30° si ottiene la curva di luce di Fig.12, molto simile a quella ottenuta per il cubo (2 massimi e 2 minimi su 180 ° di rotazione), ma con uno dei due minimi molto lungo e piatto (caratteristica trovata in parecchi casi).

Da questa analisi ultra semplicistica, sono però nati dubbi e sono iniziate sempre migliori strategie e modelli per “invertire” la curva di luce. Io stesso sono stato relatore di una tesi di una ragazza di Roma che utilizzava un modello con forme qualsiasi, modellati con tanti piccoli triangolini e poi siamo arrivati al risultato estremamente più realistico di questo lavoro. Oggi i computer permettono di andare ben oltre, anche se a volte si esagera perfino cercando di prevedere anche piccole caratteristiche geometriche locali.

L’articolo originario si può trovare QUI. Non siate troppo cattivi, in fondo era solo un primo tentativo… nemmeno Colombo è riuscito ad arrivare in Cina andando verso ovest… Comunque sia, se volete divertirvi, potete costruirvi facilmente tante belle curve d luce imponendo altre forme geometriche. Che poi gli angoli dei veri asteroidi siano un po' smussati non toglie validità ai risultati trovati.

 

QUI tutti gli articoli finora pubblicati della serie "I miei amici asteroidi"