Il matematico tedesco Dietrich Braess  pubblicò  nel 1968 un studio in cui si  dimostra che l'apertura di una nuova strada in una rete stradale non implica obbligatoriamente un miglioramento del traffico e che in determinate circostanze può provocare anzi un aumento del tempo medio di percorrenza.

Vi sembra strano? Vediamo un semplice esempio...

Smartburg è un piccolo villaggio immaginario, a 25 Km da Smart City, il capoluogo della contea di Smart County.

Nel villaggio vivono 100 famiglie, in tutto 300 abitanti, che dispongono di 200 automobili.

Non ci sono scuole di alcun grado e nessuna struttura ospedaliera.

La vita degli abitanti gravita totalmente sul capoluogo, Smart City, una cittadina di 20.000 anime, con scuole, negozi, supermercati, ospedali e una gigantesca fabbrica , la ASC Ltd, detentrice del marchio ed unica produttrice dei famosi American Smart Cookies, i biscotti per i bambini intelligenti, che ne vanno pazzi. ( almeno così recita lo spot pubblicitario)

Tutte le mattine le 200 auto partono verso Smart City; chi va in fabbrica, chi a fare compere negli Smart Stores, chi a scuola, chi semplicemente a fare un giro in città.

Ci sono due strade che collegano lSmartburg a Smart City. Furono costruite seguendo antiche piste segnate nel fitto della foresta, da due tribù dei nativi Mantouk , che abitavano nelle praterie ove oggi sorgono i due centri urbani.

Più o meno a metà strada le piste si interrompono, giusto nel punto di contatto delle due aree forestali che costituivano il territorio di caccia degli indiani, in cui essi, prima di essere esodati nelle riserve, si procuravano il cibo: daini, cervi, piccoli animali selvatici.

Ma ecco un mappa del territorio da cui si potrà capire meglio come sono realizzate le due strade di collegamento.

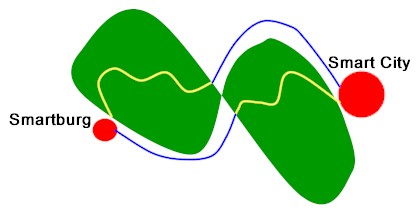
I serpeggianti tragitti gialli, nel fitto della foresta, sono le piste indiane, oggi riadattate per il traffico automobilistico; i tratti blu sono invece le strade costruite in anni più recenti, per velocizzare il percorso complessivo, sfruttando il territorio ai margini della foresta.

La strada N1, superiore, nel primo tratto, giallo, può essere percorsa in un tempo pari al numero di veicoli transitanti diviso per 10 ( se ci sono 100 veicoli, richiederà 10 minuti) la seconda parte, in blu, verrà invece percorsa nel tempo fisso di 20 minuti.

In modo del tutto simmetrico, la strada N2, inferiore, verrà percorsa nel primo tratto in 20 minuti, mentre nel secondo tratto richiederà un tempo, in minuti, pari al numero di veicoli diviso per 10.

Normalmente, data la equivalenza dei due percorsi , metà dei cittadini di Smartburg sceglie la strada superiore e l'altra metà la strada inferiore. In questo modo il tempo di percorrenza, per ciascun automobilista è sempre di 10 + 20 minuti = 30'.

Questa situazione sembrerebbe soddisfacente per tutti, e di fatto lo è, fino al giorno in cui l'ambulanza (l'unica) di Smartburg, deve far fronte ad una emergenza. Per un banale incidente domestico occorre trasportare d'urgenza un infortunato all'ospedale di Smart City. Il tempo stringe e i 30 ' di percorrenza sono decisamente troppi. Fortunatamente tutto si risolve per il meglio, ma occorre, per il futuro , trovare una soluzione che consenta alla ambulanza di giungere in un tempo più breve al pronto soccorso.

Dopo varie sedute e dopo avere esaminato le possibili soluzioni, il consiglio comunale decide che la cosa più semplice è di realizzare un bretella che unisca le due strade proprio nel punto in cui si trovano più vicine, al limite delle due aree forestali. Ecco come si intende procedere, nella figura.

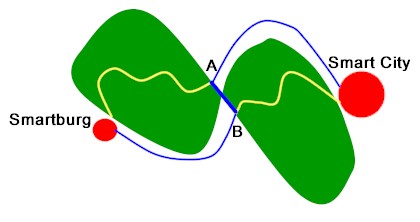
Il collegamento che verrà realizzato unirà il punto A al punto B. La brevità del tragitto ed il fatto che l'ambulanza sarà l'unico veicolo in transito su quella bretella, consentirà di passare dalla strada N1 alla N2 in un tempo trascurabile.

Il tempo di percorrenza per l'ambulanza sarà quindi dato da 10' per giungere al punto A e da altri 10 ' per andare da B a Smart City. Totale 20' invece di 30'.

Viene quindi realizzata in tempi brevi la bretella per il percorso di emergenza.

Del tutto invisibili, entriamo nelle case dei residenti, la sera della inaugurazione del nuovo tratto stradale, e ascoltiamo i loro discorsi.

Casa di Ethel e Bob Caruso

Ethel: “Sono molto soddisfatta di questa nuova strada. Pensa, se dovessi avere un bambino e avessi bisogno di arrivare velocemente all'ospedale... questa variante sarebbe davvero provvidenziale.”

Bob: “Sì, certo... ma quante volte potrà succedere? In fondo anche le emergenze sono eventi rari. Secondo me è molto utile per un altro motivo: se uno ha fretta di arrivare a Smart City ha a disposizione questa intelligente variante. L'ambulanza non è sempre in circolazione, se ci pensi, e la strada resterebbe inutilizzata, davvero un peccato, con quello che è costata.”

Ethel: “Già, sarebbe un peccato non utilizzarla.”

Casa di Marjorie e Luke Mendolia

Luke: “Bella strada, vero Ma' ? Non vedo l'ora di farla domani mattina andando in fabbrica.

Marjorie: Ma, Luke... non puoi ! E riservata alle emergenze, cioè alla ambulanza.”

Luke: “Sì, cioè...teoricamente. In realtà, dimmi perché l'ambulanza dovrebbe passare proprio all'ora in cui io vado al lavoro? Sarebbe davvero una coincidenza molto improbabile, no?”

Marjorie: “Hai ragione, non capiterà mai, e poi, anche se succedesse, un veicolo o due veicoli sulla stessa strada non fanno una gran differenza. Penso che la userò anche io per accompagnare Baby all'asilo, prima di andare a fare la spesa.”

Casa di Patricia e Jeremy Pisano

Patricia: “ Non vedo l'ora che arrivi domani mattina per provare la bretella”

Jeremy:” Ma Pat...Cosa dici? E' stata costruita solo per le emergenze di pronto soccorso, per l'ambulanza!”

Patricia:” E tu credi che i nostri vicini non abbiano già in mente di approfittare di questa opportunità? Non vorrai essere l'unico fesso che prende alla lettera le prescrizioni del consiglio, vero? “

Jeremy:”Certo che se la metti così... Domani la proviamo anche noi, questa nuova strada, così arriveremo prima in città e potremo trovare da parcheggiare più vicino al lavoro, finalmente.”

La mattina seguente 200 automobili si riversano sulla strada N1 con l'obiettivo di arrivare al fatidico punto A e commutare sulla strada numero 2, per poi raggiungere Smart City in soli 20 minuti.

Naturalmente il tempo di percorrenza del tratto fino al punto A risentirà della presenza di 200 veicoli in transito e impiegheranno 200/10 = 20' ( invece dei soliti 10). Quando tutti e 200 saranno passati da A a B, dovranno spendere altri 20' per arrivare al traguardo.

In totale ciascuno avrà impiegato 40', con un ritardo di 10' sul consueto tempo di 30'.

L'ambulanza troverà la strada intasata da 200 automobili e il suo tempo, invece dei 20' che avrebbe dovuto essere, salirà a 40', come quello di tutti gli astuti abitanti di Smartburg.

Alcune domande sorgono spontanee:

Quale perverso meccanismo si è messo in moto?

Chi, nel secolo scorso, ha maggiormente contribuito a formalizzare la dinamica di questi comportamenti, riscontrabili anche in ambito economico e inquadrabili nel più ampio contesto della teoria dei giochi?

N.B.

Qualcuno avrà notato che i cognomi dei nostri protagonisti sono tutti di origine italiana. Potrebbe essere casuale, oppure no.

P.S.

Roy Palmisano, uno dei pochi single di Smartburg, passò la notte a pensare cosa sarebbe successo la mattina del giorno seguente l'inaugurazione del nuovo tratto di collegamento.

“Certamente, conoscendo i miei concittadini, si precipiteranno tutti come falchi sul percorso dell'ambulanza. Così ci sarà un gigantesco imbottigliamento e ci metteranno non meno di 40' per arrivare a Smart City.

Se prendessi la strada blu e percorressi la bretella in senso opposto, per poi proseguire sull'altro tratto blu, non guadagnerei neppure un secondo: ci metterei in ogni caso 40' anche essendo l'unico automobilista, perché quei percorsi richiedono comunque 20' ciascuno.

C'è però una interessante alternativa. Basta che mi alzi poco prima del solito e mi metta in strada con un piccolo anticipo, ovviamente sul tragitto “riservato” all'ambulanza.

In questo modo, essendoci solo la mia auto in circolazione, potrei coprire il primo tratto giallo in 1/10 = 0,1 minuti, poi utilizzerei la bretella per portarmi sul secondo tratto giallo e lo percorrerei in un altro decimo di minuto. Totale 2 decimi di minuto, ossia 12 secondi. Più veloce della luce !

Ovviamente meglio non dire a nessuno che ho sfruttato questa possibilità. In mezzo a 200 auto chi mai si potrà accorgere se ci sono o non ci sono anche io? Basterà dire, in modo vago, che anche io, prendendo la bretella, ho notato una notevole differenza nel tempo impiegato per arrivare in città.

E non ditemi che non è vero !

 

Vi è piaciuto calcolare questo percorso? QUI ne troverete altri!