Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Un po' di riassunto

Negli articoli precedenti abbiamo costruito delle superfici in modo astratto,servendoci della topologia quoziente. Abbiamo visto superfici con bordi (cilindro e nastro) e delle superfici senza bordi (toro e sfera) che sono delle superfici chiuse. Abbiamo poi parlato di superfici orientabili e non orientabili: riprendiamo in mano il nostro cilindro con due bordi. Intuitivamente non facciamo nessuna fatica a pensare che il cilindro abbia un "dentro" e un "fuori" ovvero due facce.

E' possibile colorare la superficie del cilindro con due colori diversi, uno per la parte esterna e uno per la parte interna. Si dice in questo caso che la superficie del cilindro è orientabile. Questa è la definizione  "antica" di superficie orientabile. In pratica non è possibile passare da una faccia all'altra senza attraversare il bordo o bucando la superficie

abbiamo già visto un esempio di superficie non orientabile, che è proprio il nastro  di MÖBIUS; nell' esempio reale  del quiz di Maurizio   abbiamo toccato con mano l'impossibilità di colorare il nastro con due colori diversi, infatti se proviamo a colorare il nastro partendo da un suo punto qualsiasi, finiamo con il colorare tutto il nastro senza attraversare il bordo.

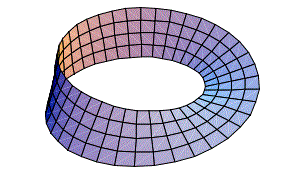
A questo punto, i matematici dicono semplicemente: una superficie non è orientabile se e solo se contiene un nastro di MÖBIUS . Questa è una definizione moderna di orientabilità.

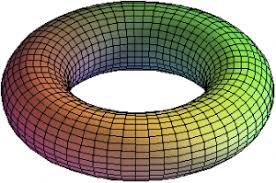
Sappiamo che toro e sfera sono superfici chiuse, e sono entrambi orientabili, hanno cioè "un dentro" e " un fuori".Ma esistono superfici chiuse non orientabili?  Si, ma non nello spazio in cui viviamo. Ci vogliono quattro dimensioni, oppure uno spazio quoziente. Una tale superficie è proprio la superficie di Klein.

Costruiamo la superficie di Klein

La superficie di Klein, anche detta bottiglia* di Klein, si costruisce come quoziente di un quadrato:

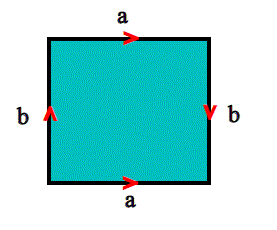
*(Il nome Bottiglia di Klein pare essere nato da una traduzione errata del termine tedesco Flache che significa superficie. Questo e stato confuso con la parola Flasche che significa bottiglia. D'altronde,la versione tridimensionale della superficie assomiglia proprio ad una bottiglia.  )

Ormai dovremmo aver capito cosa significa uno schema di questo tipo; in questo caso i lati a,a vengono incollati mantenendo l'orientamento, mentre invece i lati b,b vanno incollati invertendo l'orientamento. Consideriamo allora il solito  quadrato ;

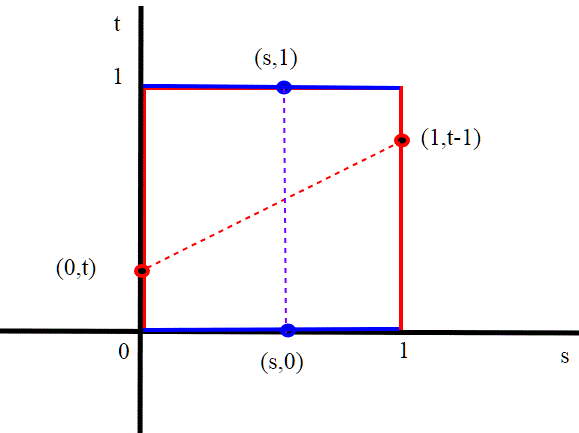
I punti interni al quadrato sono equivalenti solo a se stessi (come al solito ma questa volta ci tornerà utile)

Le coppie di  punti equivalenti, sui lati blue sono  (s,0)  (s,1); mentre sappiamo che nei lati rossi dobbiamo invertire l'orientamento,  quindi  (0,t)  (1,t-1) . La superficie di Klein così definita è lo spazio quoziente , che sappiamo essere uno spazio topologico. Però non riusciamo a trovare una funzione parametrica che ne dia l'immagine nello spazio euclideo tridimensionale.

Facciamo un tentativo "pratico" di visualizzare la bottiglia di Klein. Incollando i lati a,a otteniamo come di consueto il cilindro.

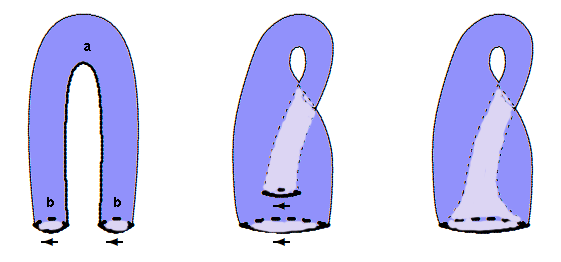
a questo punto, se i lati b che nel contempo sono diventati dei cerchi, andassero incollati nello stesso verso, potremmo incollarli direttamente, come nel toro. Ma  non è così; inventiamo allora l'espediente di "bucare" la superficie cilindrica; in questo modo possiamo incollare correttamente i due bordi. Questo è quello che bene o male fanno tutti, anche con stupende animazioni. Ma questa non è la vera bottiglia di Klein. Perchè? Quando buchiamo la superficie, otteniamo una identificazione di punti sulla superficie del cilindro.

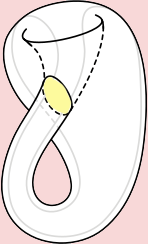
Ma sappiamo che questi punti, essendo interni al quadrato generatore, corrispondono solo a se stessi. Quindi in realtà questo buco non può esistere. Esiste una parametrizzazione della bottiglia di Klein in quattro dimensioni, ma chiaramente non può darci nessun risultato visivo. Intuitivamente, in quattro dimensioni si riesce ad evitare il buco per congiungere i

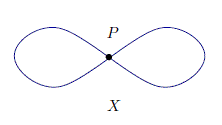
bordi come in tre dimensioni si riesce a congiungere  gli estremi di una linea per ottenere una forma a otto non intersecata..

Ma allora come facciamo a capire quali proprietà abbia la bottiglia di Klein? Possiamo usare solo la la topologia.

Una parametrizzazione della superficie di Klein in  .

Consideriamo la funzione parametrica f:X= data dalle espressioni:

f(s,t)=

al solito, definiamo g([p])=f(p). Si verifica con un po' di pazienza* che ,

(* per una volta ometto i calcoli; basta sostituire punti equivalenti, (s,0)  (s,1), (0,t)  (1,t-1) in f(s,t) e vedere che individuano lo stesso punto).

Quindi g è ben definita. Inoltre gli unici punti** in cui f non è iniettiva sono proprio quelli equivalenti, corrispondenti alle saldature dei bordi. Quindi la superficie non si autointerseca.

(** anche questa affermazione andrebbe provata rigorosamente).

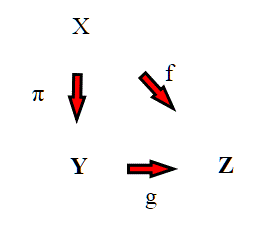
Al solito poniamo Z=f(X). f è continua, quindi Z è compatto. Ma allora , per il solito Teorema, g è un omeomorfismo dello spazio quoziente  (superficie di Klein) in Z=f(X).  Quindi la superficie di Klein è omeomorfa a Z=f(X).

Z è inoltre senza  bordi, quindi la superficie Z è una superficie chiusa:

La bottiglia di Klein  è una superficie chiusa.

Nell'articolo sulle varietà topologiche, e come accennato sopra, abbiamo visto la definizione di superficie non orientabile:

una superficie non è orientabile se e solo se contiene un nastro di MÖBIUS .

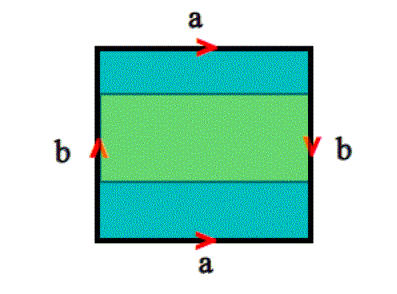
come si vede dalla figura,la bottiglia di Klein contiene un nastro di MÖBIUS (la parte verde)

La bottiglia di Klein è una superficie chiusa  non orientabile.