Giochiamo con i perimetri... */** (CON SOLUZIONE)
Divertiamoci un po' con della geometria semplice semplice. Due quiz relativi a un qualsiasi triangolo, che trovo molto divertenti e stimolanti... Come al solito, un pacco di “niente” a chi propone la migliore soluzione, ossia quella più rapida, con meno formule matematiche (e più ragionamento) e più elegante.
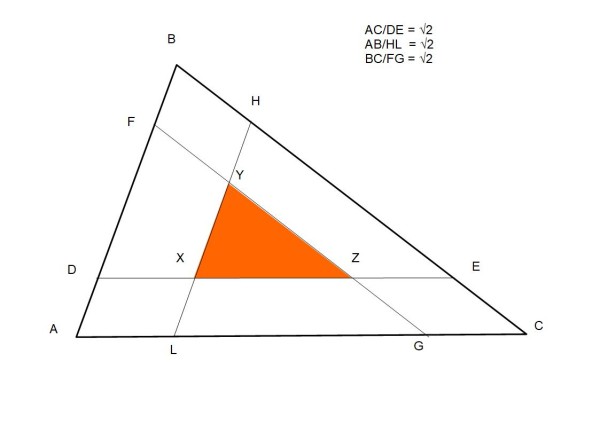
1*) In Fig. 1, prendiamo un triangolo ABC qualsiasi e poi, lato per lato, tracciamo parallelamente al lato, un segmento che stia con lui nel rapporto 1/√2. In tal modo si ottiene il triangolo XYZ. Determinare il rapporto tra il perimetro di XYZ e il perimetro di ABC.
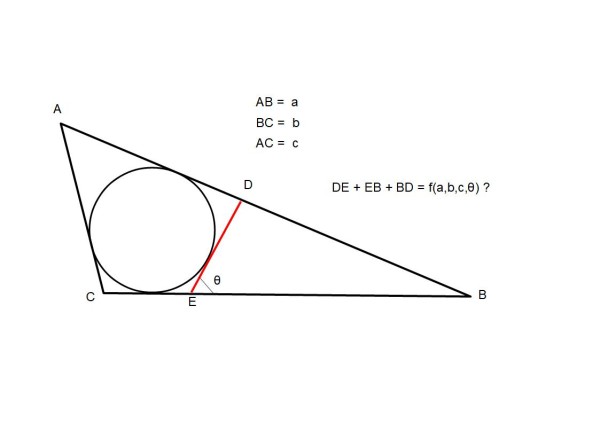
2**) In Fig. 2, consideriamo il triangolo ABC e iscriviamo in esso un cerchio. Tracciamo una qualsiasi tangente DE al cerchio e determiniamo il perimetro del nuovo triangolo DEB così determinato in funzione dei tre lati e dell'inclinazione della tangente rispetto a una asse scelto a piacere.
Soluzioni nei commenti:
Quelle proposte da Maurizio sono non solo giuste (come quella di Arturo) ma estremamente brevi ed eleganti. Tanti complimenti e un bel regalo... virtuale!






4 commenti
Rispondo solo al primo quesito
Intanto , per evitare di usare l'equation editor , e anche er generalizzare, al posto di radice quadrata di 2 considero un parametro generico k.
Dalla similitudine dei triangoli DBE ed ABC si ha:
DB/AB=DE/AC
da cui:
DB=AB*DE/AC
ma, essendo per ipotesi DE=AC/k (nel nostro caso k=radice quadrata di 2), si ottiene:
DB=AB/k
Analogamente, considerando la similitudine dei triangoli FGA ed ABC, si ha:
FA/AB=FG/BC
da cui
FA=AB*FG/BC
Anche in questo caso, essendo per ipotesi FG=BC/k, si ottiene:
FA=AB/k
Quindi vediamo che DB=FA
Ma essendo DB=AB-AD e FA=AB-FB, se ne deduce che AD=FB. Indico con a la lunghezza di questi due segmenti uguali.
Posso ora scrivere che
DB+a=AB
da cui
a=AB-DB
cioé, per l'espressione di DB prima trovata:
a=AB-AB/k
cioè:
a=AB(1-1/k)
Ora, per costruzione, FB=YH e AD=XL, cioè YH=XL=a
Ma allora XY, lato del triangolo interno, sarà dato da:
XY=HL-2a
Sostituendo le espressioni note di HL ed a si ottiene:
XY=AB/k-2*AB(1-1/k)
svolgendo i calcoli si ottiene:
XY=AB*(3/k-2)
Dividendo ora XY per AB ottengo il rapporto tra tali due lati:
XY/AB=3/k - 2
Nel nostro caso il risultato è 0,1213. Ora, ripetendo il ragionamento per gli altri due lati del triangolo interno, si ottiene sempre lo stesso risultato. Di conseguenza, facendo la somma dei 3 lati del triangolo interno, alla fine posso affermare che il rapporto dei perimetri è proprio 0,1213.
Rispondo anche io alla prima domanda.
I due triangoli ABC e xyz hanno lo stesso baricentro. Se i lati di ABC vengono tracciati parallelamente, ridotti a 2/3, passano per il baricentro e il perimetro Pxyz vale Zero.
Questa figura illustra come varia il perimetro al variare della proporzione tra i lati xyz e ABC:
Scrivo la proporzione P ABC :(1-2/3) = Pxyz ( 1/rad 2 - 2/3) da cui ricavo Pxyz
Pxyz = 3 ( 1/rad 2 - 2/3) = 0,1213203456
e il secondo?
Questo ?
Traccio i raggi ( blu) in corrispondenza ai punti di tangenza triangolo cerchio
Osservando le simmetrie dei due quadrilateri AROP e CROQ noto che:
AP = AR e CQ=RC quindi
AP + CQ = a e conseguentemente
QB + PB = b+c-a
Inoltre, per la simmetria del quadrilatero POQB, PB = QB = (b+c-a)/2
Ora traccio il raggio OT in corrispondenza al punto di tangenza del cerchio con ED
dalle simmetrie dei due quadrilateri QOTE e POTD noto che
QE=TE PD=TD qualsiasi sia l'angolo teta
Pertanto BD+DP = BD+DT e BE+EQ = BE+ET
Il perimetro cercato DE + EB +BD è quindi la somma dei segmenti PB e QB = b+c-a
ed è indipendente dall'angolo teta.