QUIZ:Un luogo misterioso... ***(con soluzione nei commenti)
Per affrontare questo problema bisogna sapere cos'è la distanza punto-retta e cosa si intende per luogo geometrico.
Distanza punto retta:
Data una retta r e un punto P la distanza punto retta è la minima distanza fra il punto e i punti appartenenti alla retta. In pratica tale distanza si ottiene tracciando la perpendicolare alla retta r passante per il punto P.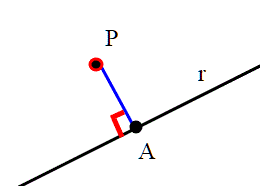 
La distanza è la lunghezza del segmento PA.
Luogo geometrico del piano.
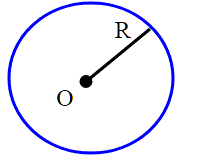
E' l'insieme dei punti del piano che hanno una determinata proprietà. Ad esempio, una circonferenza è il luogo geometrico dei punti equidistanti da un punto fisso O ,che è il centro.
La domanda del quiz è la seguente:
Consideriamo due rette complanari r,s non parallele.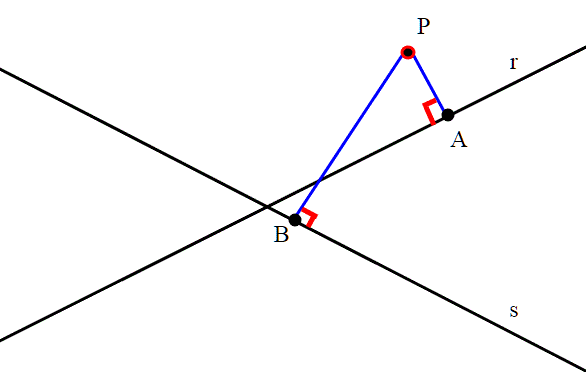 
Sia P un punto del piano; indichiamo con le distanze del punto P dalle rette s,r. Qual'è il luogo geometrico dei punti per cui la somma di tali distanze è costante, cioè uguale ad un certo valore positivo K ?
(In formule: =cost=K.)
Non inserisco la soluzione, ho notato che anche nascondendola con lo show/hide, i quesiti perdono un po' di interesse. La lascio a voi.
57 commenti
intendi il luogo geometrico descritto dal punto P con B e A fissi? Mi sembra strano... (tre asterischi). Se non è così puoi spiegarti meglio?
si parla di distanza dalle rette. No A e B non sono fissi.
Se ho capito bene occorre trovare tutti i punti, come P' in questa immagine.
ribadisco che Non c'è scritto da nessuna parte che A e B siano fissi. Le rette r, s sono fisse. Le proiezioni di P variano. Si chiede quando la somma delle distanze PA e PB dalle rette sia costante.
spero che adesso almeno il testo del quiz sia chiaro. Cercando di esemplificare forse ho creato confusione.
Mi sembrava troppo ermetico scrivere :
Date nel piano due rette che si intersecano, trovare il luogo dei punti L tale che la somma delle distanze dei punti di L da ciascuna retta sia uguale a un dato valore.
Maurizio: si, il tuo disegno va bene ma bisogna aggiungere che la somma delle distanze PA+PB=P'A'+P'B'=K
In pratica è come dice Maurizio... se traccio la parallela a s passante per P, è accettabili il punto di essa che abbia distanza da r uguale a PA?
Se è così è molto carino e si può risolvere anche solo graficamente... penso.
mi sembra che Maurizio abbia tracciato le perpendicolari alle rette e giustamente. Il quiz non è immediato e ci vuole una dimostrazione o geometrica o analitica. L'incognita é una figura geometrica nota, e fra l altro molto semplice. Ho messo tre pallini ma in realtà..
Dico solo qualcosa per lasciare disponibile il quiz ad altri lettori, spero che sia una intuizione corretta.
figura di riferimento:
traccio le linee verdi di lunghezza K=AP+BP perpendicolari alle rette r ed s in modo che quella perpendicolare a r individui su s il punto Q. Quella perpendicolare a s individua su r il punto R.
Poi traccio le linee viola di lunghezza K=AP+BP perpendicolari alle rette r e s e individuo, analogamente a quanto detto prima i punti S e T.
Unisco i quattro punti ottenendo il rettangolo QRST, luogo dei punti P cercato.
Lascio aperta la discussione sulla dimostrazione.
intanto grazie Maurizio.
Le infinite rette perpendicolari formano un reticolo di rombi. La congiungente dei vertici del rettangolo è somma di diagonali di rombi. Per semplicita creiamo un solo rombo. Costruiamo un triangolo rettangolo con ipotenusa coincidente con la diagonale maggiore del rombo. È sufficiente dimostrare che l a parallela al lato del rombo, tracciata dal centro del rombo fino al cateto del triangolo è la metà del cateto del triangolo rettangolo. Lo è per la simmetria del rombo. Questo vale per qualsiasi rombo, di qualunque dimensione si costruisca. Scusate ma posso disegnare ...
si Leandro. riesci a fare un disegno?
Se le rette date fossero perpendicolari, il luogo dei punti sarebbe un quadrato di lato k*sqrt(2)
una volta compreso che si tratta di un rettangolo, bisogna adesso dimostrarlo. Faccio notare che le rette dividono il rettangolo in quattro triangoli isosceli ..
Non lo scrivo ancora per esteso... ma da un punta di vista geometrico si possono determinare i punti più lontani dall'intersezione delle rette e poi basta dimostrare l'uguaglianza di due triangoli per arrivare al rettangolo... appena posso lo dimostro graficamente.
cerea...
Come posso allegare un'immagine?
bisogna prima caricarla su un server tipo imgur e poi mettere l url usando l icona immagine
Consideriamo solo un quadrante. Il punto di massima distanza dal centro che soddisfi la relazione è B. Quali sono gli altri punti lungo la sua verticale? Devono essere quelli per i quali CA + CN = k. Ma k = MD + DB. Dato che CN =DN, basta dimostrare che AC = DB ... E questi sono ovviamente gli unici punti accettabili.
Dopo di che la stessa situazione vale per gli altri quadranti...
Ma vi sono anche altri triangoli che portano alla stessa soluzione...
Oppure, analiticamente, si scrivono le distanze da un punto a due rette date (ricordiamoci le rette perpendicolari) e si impone che la somma delle distanze sia uguale a k.... buon divertimento....
bel quiz, semplice ma pieno di possibilità. Bravo Umberto!
Visto che i lavori procedono..
Questa è la figura che completa il mio precedente commento.
grazie. Io l' ho risolto analiticamente. Sono un po' negato coi triangoli. Ambedue le soluzioni si semplificano però notevolmente.
non riesco a capire Maurizio; tu proietti due volte lo stesso punto P ma la proiezione é una sola. Bisogna invece proiettare un punto diverso sullo stesso lato del rettangolo e vedere che la somma delle distanze dalle due rette é la stessa.
Propongo un ragionamento che partendo da una punto generico (x,y), senza ipotesi sulla sua collocazione, impone la condizione indicata del quiz.
Il problema ha i due assi di simmetria indicati in figura con le rette tratteggiate. Basta risolverlo in un quadrante. Il resto si ottiene ribalatando le soluzioni rispetto agli assi. Quindi limito la soluzione al 1° quadrante (in alto a destra).
La condizione indicata dal quiz è che valga la relazione k=k1+k2, con k costante.
Per comodità identifico il punto (x,y) con le sue coordinate polari})
. I due tipi di coordinate sono legate tra loro dalla trasformazione \;&space;,\;&space;y=r&space;sin(\varphi)})
Noto che k1 e k2 sono cateti di due triangoli retti con ipotenusa r. Gli angoli opposti ai due cateti sono})
per k1 e })
per k2
Le relazioni trigonometrica che legano i due cateti ad r sono quindi:
Ora applico le relazioni che legano il seno di una somma/differenza tra due angoli con le funzioni trigonometriche dei singoli angoli.
![\small \boldsymbol{k1\! =\! r sin(\alpha\! -\! \varphi)=r [sin(\alpha) cos(\varphi)\! -\! cos(\alpha) sin(\varphi)]}\; \; \mathrm{per}\; \boldsymbol{0\!>\! \varphi\!>\!\alpha}](http://latex.codecogs.com/gif.latex?\small&space;\boldsymbol{k1\!&space;=\!&space;r&space;sin(\alpha\!&space;-\!&space;\varphi)=r&space;[sin(\alpha)&space;cos(\varphi)\!&space;-\!&space;cos(\alpha)&space;sin(\varphi)]}\;&space;\;&space;\mathrm{per}\;&space;\boldsymbol{0\!>\!&space;\varphi\!>\!\alpha})
![\small \boldsymbol{k1\! =\! r sin(\varphi\! -\! \alpha)=r [-sin(\alpha) cos(\varphi)\! +\! cos(\alpha) sin(\varphi)]}\; \; \mathrm{per}\; \boldsymbol{\alpha\!>\! \varphi\!>\!90^{\circ}}](http://latex.codecogs.com/gif.latex?\small&space;\boldsymbol{k1\!&space;=\!&space;r&space;sin(\varphi\!&space;-\!&space;\alpha)=r&space;[-sin(\alpha)&space;cos(\varphi)\!&space;+\!&space;cos(\alpha)&space;sin(\varphi)]}\;&space;\;&space;\mathrm{per}\;&space;\boldsymbol{\alpha\!>\!&space;\varphi\!>\!90^{\circ}})
La relazione che vincola la posizione del nostro punto (x,y) è k1+k2=k. Vado a sostituire in questa relazione le espressioni ottenute per k1 e k2.
![\small \boldsymbol{k1\! =r [sin(\alpha) cos(\varphi)\! -\! cos(\alpha) sin(\varphi)]}](http://latex.codecogs.com/gif.latex?\small&space;\boldsymbol{k1\!&space;=r&space;[sin(\alpha)&space;cos(\varphi)\!&space;-\!&space;cos(\alpha)&space;sin(\varphi)]})
![\small \boldsymbol{k2\! =r [sin(\alpha) cos(\varphi)\! +\! cos(\alpha) sin(\varphi)]}](http://latex.codecogs.com/gif.latex?\small&space;\boldsymbol{k2\!&space;=r&space;[sin(\alpha)&space;cos(\varphi)\!&space;+\!&space;cos(\alpha)&space;sin(\varphi)]})
+ +
=
per 0>phi>alpha
k1+k2=r [sin(alpha) cos(phi)-cos(alpha) sin(phi)]+r [sin(alpha) cos(phi)+cos(alpha) sin(phi)]=2 r sin(alpha) cos(phi)=k
quindi r=k/(2 r sin(alpha) cos(phi))
Per ottenere i valori di x e y dovo sostituire questa espressione di r nelle trasformazioni
La sequenza logica della mia soluzione è la seguente:
3. Allora, per la prima proposizione, anche le coordinate blu mantengono la loro somma costante.
Come concludevo precedentemente, questa costruzione si applica a tutti i quadranti e ne esce la figura del rettangolo come luogo di punti cercato.
Inizialmente avevo scritto questa soluzione, partendo dalla figura del primo commento, ma mi sembra che la trasformazione di coordinate sia una impostazione più originale.
Fabrizio, Maurizio mi piacciono molto le vostre idee ma mi state mettendo in crisi. La soluzione del quiz sia geometrica che analitica è molto più semplice. Occupa poche righe. Il mio intento era quello di non gestire cose troppo complicate.
Scusate, il mio commento precedente è partito incompleto. Questo lo sostituisce e le completa.
Non avendo alcun intuito geometrico, propongo un ragionamento che parte da una punto generico (x,y) del luogo dei punti che cerchiamo, senza ipotesi sulla sua collocazione. Il risultato è ottenuto imponendo che questo punto soddisfi la condizione indicata del quiz.
Il problema ha i due assi di simmetria indicati in figura con le rette tratteggiate. Basta risolverlo in un quadrante, il resto si ottiene ribalatando le soluzioni rispetto agli assi. Quindi limito la soluzione al 1° quadrante (in alto a destra).
La condizione indicata dal quiz è che valga la relazione k=k1+k2, con k costante.
Per comodità identifico il punto (x,y) con le sue coordinate polari})
. I due tipi di coordinate sono legate tra loro dalla trasformazione \;&space;,\;&space;y=r&space;sin(\varphi)})
Noto che k1 e k2 sono cateti di due triangoli retti con ipotenusa r. Gli angoli opposti ai due cateti sono})
per k1 e })
per k2
Le relazioni trigonometrica che legano i due cateti ad r sono quindi:
Nota: k1 è una distanza quindi una grandezza positiva, per questo occorre cambiare i segni agli angoli.
Ora applico le relazioni che legano il seno di una somma/differenza tra due angoli con le funzioni trigonometriche dei singoli angoli.
![\small \boldsymbol{k1\! =\! r sin(\alpha\! -\! \varphi)=r [sin(\alpha) cos(\varphi)\! -\! cos(\alpha) sin(\varphi)]}\; \; \mathrm{per}\; \boldsymbol{0\!>\! \varphi\!>\!\alpha}](http://latex.codecogs.com/gif.latex?\small&space;\boldsymbol{k1\!&space;=\!&space;r&space;sin(\alpha\!&space;-\!&space;\varphi)=r&space;[sin(\alpha)&space;cos(\varphi)\!&space;-\!&space;cos(\alpha)&space;sin(\varphi)]}\;&space;\;&space;\mathrm{per}\;&space;\boldsymbol{0\!>\!&space;\varphi\!>\!\alpha})
![\small \boldsymbol{k1\! =\! r sin(\varphi\! -\! \alpha)=r [-sin(\alpha) cos(\varphi)\! +\! cos(\alpha) sin(\varphi)]}\; \; \mathrm{per}\; \boldsymbol{\alpha\!>\! \varphi\!>\!90^{\circ}}](http://latex.codecogs.com/gif.latex?\small&space;\boldsymbol{k1\!&space;=\!&space;r&space;sin(\varphi\!&space;-\!&space;\alpha)=r&space;[-sin(\alpha)&space;cos(\varphi)\!&space;+\!&space;cos(\alpha)&space;sin(\varphi)]}\;&space;\;&space;\mathrm{per}\;&space;\boldsymbol{\alpha\!>\!&space;\varphi\!>\!90^{\circ}})
La relazione che vincola la posizione del nostro punto (x,y) è k1+k2=k. Vado a sostituire in questa relazione le espressioni ottenute per k1 e k2.
Prima lo faccio per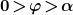
![\small \boldsymbol{k1\! =r [sin(\alpha) cos(\varphi)\! -\! cos(\alpha) sin(\varphi)]}](http://latex.codecogs.com/gif.latex?\small&space;\boldsymbol{k1\!&space;=r&space;[sin(\alpha)&space;cos(\varphi)\!&space;-\!&space;cos(\alpha)&space;sin(\varphi)]})
![\small \boldsymbol{k2\! =r [sin(\alpha) cos(\varphi)\! +\! cos(\alpha) sin(\varphi)]}](http://latex.codecogs.com/gif.latex?\small&space;\boldsymbol{k2\!&space;=r&space;[sin(\alpha)&space;cos(\varphi)\!&space;+\!&space;cos(\alpha)&space;sin(\varphi)]})
\:&space;cos(\varphi)})
+ +
= =
da cui\:&space;cos(\varphi)}})
Per ottenere i valori di x e y devo sostituire questa espressione di r nelle trasformazioni indicate sopra
Per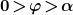
, x è una costante, quindi il luogo dei punti che cerchiamo è un segmento verticale che parte dall'asse delle x ed arriva alla retta superiore.
Facendo il ragionamento analogo per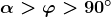
ottengo
+ +
= =
da cui\:&space;cos(\alpha)}})
e
Per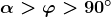
, cioè sopra la retta superiore, y è costante. Il luogo dei punti che cerchiamo è un segmento orizzontale che va dall'asse verticale alla retta superiore.
ok Fabrizio.Anche se può spaventare.
grazie
Per motivi opposti a quelli di Fabrizio, sul tipo di intuito, persevero con la visione geometrica, così siamo complementari.
Invito a riflettere qua questa immagine in cui ho ribaltato specularmente metà del disegno originale, aggiungendo qualcosa.
Il punto P e il suo speculare individuano un segmento perpendicolare alla bisettrice tra le rette r e s (EB).
Le intersezioni del prolungamento di questo segmento, a sinistra e destra, individuano C e D sulle rette r e s .
BC=BD = k
Traccio dal punto E le perpendicolari a r e s e trovo F e G. Per simmetria EF=FG = K/2 (da dimostrare )
Lascio il ragionamento , visto che devo uscire velocemente di casa, a chi abbia voglia di continuare.
Mi spiace essere del tutto trascurato, ma la soluzione da me proposta era identica a quella proposta dopo da Maurizio. A me sembra estremamente semplice e immediata...
non è questione di trascuratezza.. ma della mia limitatezza nel capire subito tutte le idee.
Alla fine faremo un resoconto completo di tutto.
Ancora più semplice...Da P tale che PH = K traccio la parallela a r. Per qualsiasi punto di questa retta traccio la perpendicolare a r. Prendiamo il punto Q e la sua perpendicolare. Sul segmento QT dove starà il punto tale che le sue due perpendicolari alle rette diano come somma K. QT è uguale a K. il punto R deve avere RT + RV = K e quindi RV deve essere uguale a RQ. Il solo modo per avere questa uguaglianza è che il triangolo RQV sia isoscele, ossia che RP sia parallela all'asse orizzontale OM. E questo vale per qualsiasi punto della retta parallela... e per tutti i vari settori. Una costruzione quasi immediata... OK, per me basta...
Questo è già un altro discorso. È una dimostrazione
Concludo il mio ultimo commento...
Invito a riflettere su questa immagine in cui ho ribaltato specularmente metà del disegno originale, aggiungendo qualcosa.
Il punto P e il suo speculare individuano un segmento perpendicolare alla bisettrice tra le rette r e s (EB).
Le intersezioni del prolungamento di questo segmento, a sinistra e destra, individuano C e D sulle rette r e s .
BC=BD = k
Traccio dal punto E le perpendicolari a r e s e trovo F e G. dimostro che EF=FG = K/2
Infatti: il punto G è intermedio per costruzione tra A e Bspeculare (Bs)
Quindi EG è intermedio tra PA e PBspeculare (PBs) , e poiché PA+PB=k allora EG = K/2 (e anche EF) .
Spostando il punto P lungo il segmento ED si sposta simmetricamente anche l'immagine speculare. I punti A e Bs si riposizionano simmetricamente rispetto a G , come As e B si riposizionano simmetricamente rispetto a F , e avremo sempre la medesima relazione trovata rispetto al segmento EG e al suo speculare EF, che restano fissi. Ne consegue che in ogni caso PA+PB = k
Il ragionamento si estende per simmetria dal tratto ED al tratto CE e poi a tutti i quadranti, giungendo alla conclusione che il luogo dei punti cercati è il famoso rettangolo.
ok Maurizio. Grazie per il tuo solito importante contributo.
Grazie a te per questo bel quiz.
Se qualcuno trae delle conclusioni da questo disegno:
la cosa si semplifica ulteriormente
La frase da dimostrare è : Dato un triangolo isoscele, consideriamo i punti del lato "singolo". La somma delle distanze di ogni suo punto dai lati uguali è una costante. Per dimostrarlo direi che bisogna lavorare con alcuni triangoli come fatto nei metodi proposti da Mau e da me... o sbaglio?
si la frase da dimostrare é propri quella.
no e un metodo alternativo. La costruzione è tutta li. Basta dire qualcosa
Considero l'area del triangolo isoscele ABC come somma delle aree di APB e BPC
Area = AB*H1P + BC*H2P
ma AB=BC quindi Area = AB ( H1P + H2P )
Dato che Area e AB restano uguali al variare della posizione di P sul lato AC, significa che H1P+H2P = costante.
Osservo che la differenza tra questo ultimo disegno e la figura originale del quiz consiste nel fatto che l'angolo ABC adesso è inferiore a 90° mentre nel disegno del quiz era maggiore di 90°.
L'angolo > 90° comporta la conseguenza che H1 ( o H2) possono trovarsi oltre il vertice del triangolo isoscele
Non credo che sia per caso che la scelta del punto P, nella figura del quiz sia stata fatta proprio in modo che uno dei due punti (B ) sia oltre il vertice del triangolo isoscele.
Nel caso di angolo = 90° siamo al limite, come in questa figura, in cui H1 e H2 arrivano al massimo a B
la proprietà vale però lo stesso
Verissimo, la proprietà vale comunque, ma quello che intendevo dire è che con un angolo > 90° è possibile presentare una figura in cui uno dei punti H esce dalla superficie del triangolo isoscele, come nel disegno del quiz.
La conseguenza è questa...
ABC è il triangolo isoscele (AB=BC) e l'angolo ABC è > 90°. P è posizionato in modo che H1 cada fuori dall'area di ABC
Ora sposto (frecce rosse) P in P1, in modo che H1 vada in H1'(=B) e conseguentemente H2 vada in H2'.
Si vedono chiaramente le due aree adiacenti ABP' e BP'C che sommate danno l'area ABC ed è' immediato risalire alla proprietà (somma delle altezze = costante) per tutti i punti tra P' e il suo speculare.
Facendo invece riferimento alla collocazione iniziale nel punto P, si perde la corrispondenza visiva tra le aree. La corrispondente soluzione analitica, che non soffre della "dipendenza visiva" non presenta questo problema.
Con un angolo ABC <= 90° questa configurazione non si sarebbe potuta realizzare.
non si vede visivamente. Anch'io c'ero cascato . Ma ti ripeto che é la stessa cosa. L area é sempre base per altezza anche se l altezza va fuori dalla base. E le due aree compongono sempre l area totale del triangolo isoscele.
Concludo....
Le coppie di aree si vedono in ogni caso, ma per il fatto che nella figura del quiz una altezza ( H1) "cade fuori dal triangolo" viene persa la immediatezza della percezione. E' più che altro un condizionamento psicologico.
Ecco le due figure...
ho cercato di fare la figura più generica possibile. Non volevo mettere fuoristrada nessuno. Comunque hai ragione su un fatto; meglio la via analitica.io ho usato quella.
Beh... analiticamente diventa banale ricordando che le due rette hanno equazione y = ax e y = -ax e che
d1 = abs(yo - axo)/(1 + a2)1/2
d2 = abs(y0 + axo)/(1 + a2)1/2
e che d1 + d2 = k
e mi fermo qui...
si, più o meno è cosi. Bisogna solo semplificare usando le espressioni dei valori assoluti
Francamente avevo iniziato a scrivere la mia soluzione proprio con le distanze. Ma poi mi è sembrato più semplice il metodo trigonometrico che ho proposto sopra. Visto che lo avevo già in buona parte scritto, a questo punto lo propongo semplificato eliminando lo sviluppo per ricavare l'espressione della distanza punto-retta.
Utilizzo le coordinate cartesiane definite dai due assi di simmetria.
Indico con)
le coordinate di un punto generico sul luogo dei punti che cerchiamo. Lo colloco nel 1° quadrante poiché, trovata la soluzione in questo quadrante, può essere estesa agli altri sfruttando le simmetrie.
Nel sistema di coordinate utilizzato, le equazioni delle due rette sono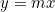
e 
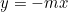, con =\frac{sin(\alpha)}{cos(\alpha)})
, dove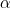 
è l'angolo tra retta ed asse orizzontale.
Le distanze del punto dalle due rette, che chiamo k1 e k2, sono
Per i punti sopra la retta superiore, dove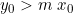
e quindi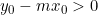 
![\small k=k1+k2= [(y_0-m x_0)+(y_0+m x_0)] cos(\alpha)=2\;y_0\;cos(\alpha)](http://latex.codecogs.com/gif.latex?\small&space;k=k1+k2=&space;[(y_0-m&space;x_0)+(y_0+m&space;x_0)]&space;cos(\alpha)=2\;y_0\;cos(\alpha))
Da cui})
Sopra la retta superiore,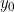
è costante. Il luogo dei punti che cerchiamo qui è un segmento orizzontale che va dall'asse verticale alla retta superiore.
Per i punti sotto la retta superiore, dove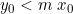
, per mantenere positivo k1 occorre cambiare i segni dei due addendi che lo compongono
![\small k=k1+k2= [(-y_0+m x_0)+(y_0+m x_0)] cos(\alpha)=2\;m\; x_0\;cos(\alpha)](http://latex.codecogs.com/gif.latex?\small&space;k=k1+k2=&space;[(-y_0+m&space;x_0)+(y_0+m&space;x_0)]&space;cos(\alpha)=2\;m\;&space;x_0\;cos(\alpha))
Utilizzando la definizione di m, diventa
Da cui})
Sotto la retta superiore,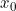
è costante. Il luogo dei punti che cerchiamo qui è un segmento verticale che va dall'asse orizzontale alla retta superiore.
OK Fabrizio, si la formula della distanza può essere data per nota. A Questo punto (questa era più o meno la mia soluzione anlitica) forse è inutile che io la scriva. Per il resto , c'è la parte geometrica su cui tanto hanno scritto Vincenzo e Maurizio. Boh, vedrò.
in realtà, è inutile introdurre l'angolo, dato che la quantità 1/(1 + m2)1/2 è un termine noto...
Ad occhio, sembrerebbe che a e b siano i due fuochi di un ellisse e p un punto facente parte del luogo geometrico dei punti corrispondente all’ellisse stesso.
grazie del commento Cesare ma come scritto sopra nelle risposte il luogo geometrico é un rettangolo.
No, mi correggo, si perderebbe l’ortogonalitá dei segmenti PA e PB con le relative rette...
Credo sia la bisettrice dell'angolo che formano le rette r e s
no Claudio é un rettangolo come puoi vedere dai commenti.comunque grazie.
Ho spostato il quiz nell'archivio, ovvero nell'angolo dei quiz. Ritengo i commenti molto esaurienti, vi invito a leggerli .Affido ad essi la soluzione.