Categorie: Fisica Fisica di Papalla Relatività
Tags: orologio di luce
Scritto da: I Papallicoli
Commenti:19
UN OROLOGIO DAVVERO ILLUMINANTE *
Questo articolo è inserito nella sezione d'archivio dedicata alla Relatività Ristretta
Il Pianeta fotone era famoso per le sue precisissime fabbriche di orologi luce.
Tutti gli orologi che venivano fabbricati lì, erano perfettamente identici.
Il principio di funzionamento si basava sulla velocità della luce nel vuoto, che oltre ad essere costante era sempre la stessa e poco importava se si era comodamente seduti su una poltrona a casa oppure se ci si trovava sulla plancia di una veloce astronave.
La luce, o meglio i nostri amici fotoni, rimbalzavano continuamente tra due specchi, posti ad una distanza prestabilita, misurata in fabbrica con una precisione migliaia di volte inferiore alle dimensione di un protone.
Il fotone partiva da uno specchio, tic, rimbalzava sull’altro, tac, tornava allo specchio iniziale, tic e così via all’infinito!
In fabbrica era appena arrivata la richiesta di acquistare due orologi luce, che i dubbisti (abitanti del pianeta noncicredosenonvedo) volevano utilizzare per un esperimento.
I fabbricanti di orologi prima di consegnare la preziosa merce, avevano avvertito i dubbisti che solo la luce è costante, ossia viaggia sempre alla stessa velocità, mentre la misura del tempo e dello spazio non lo è affatto poiché può cambiare da un luogo ad un altro, così come da un sistema di riferimento ad un altro.
I dubbisti non avevano prestato molta attenzione a quello strano avvertimento, ma ben presto si sarebbero accorti di cosa intendevano dire i fabbricanti di orologi luce.
L’esperimento che intendevano realizzare prevedeva quattro diverse fasi.
La prima fase consisteva nel posizionare un orologio luce su un treno che, per chi si trovava seduto sulla panchina di una stazione ferroviaria, viaggiava a velocità costante.
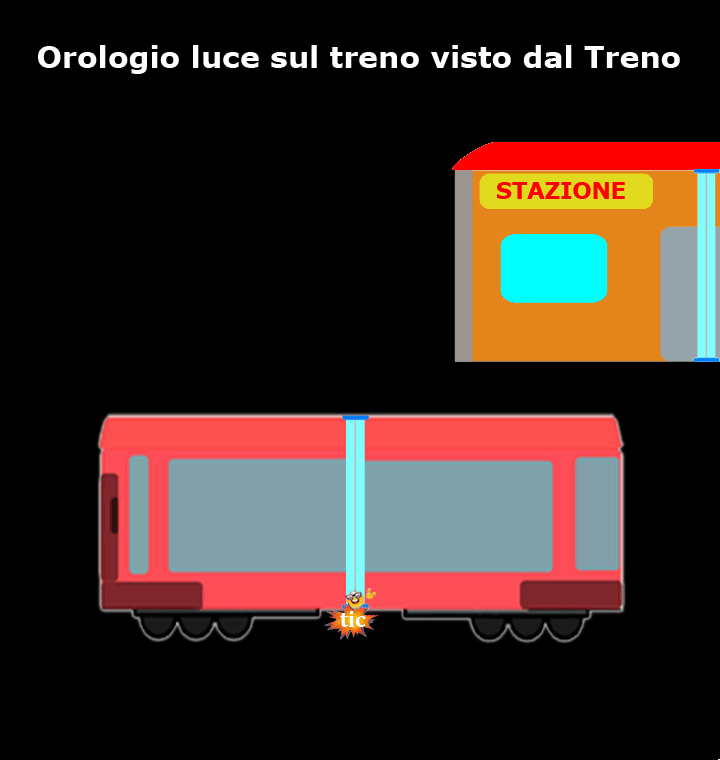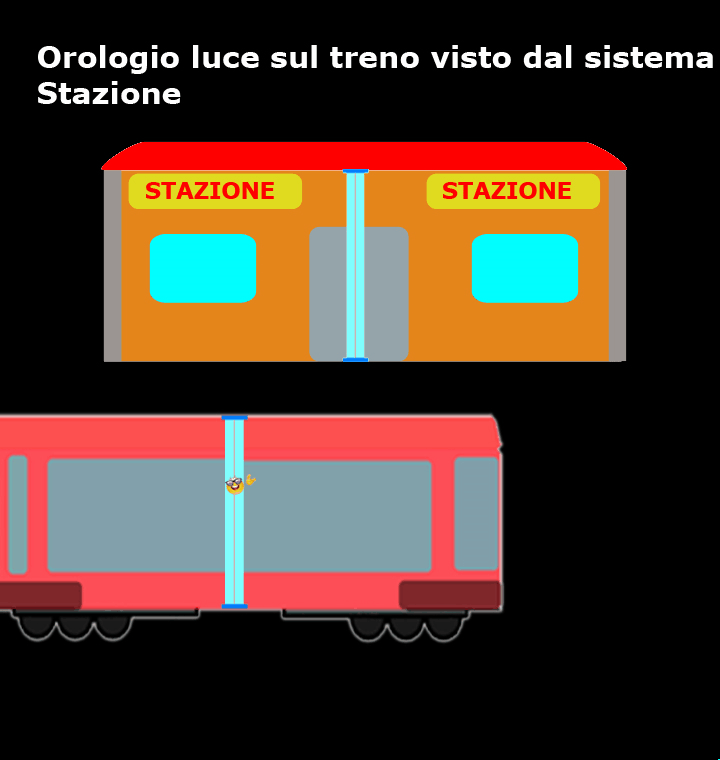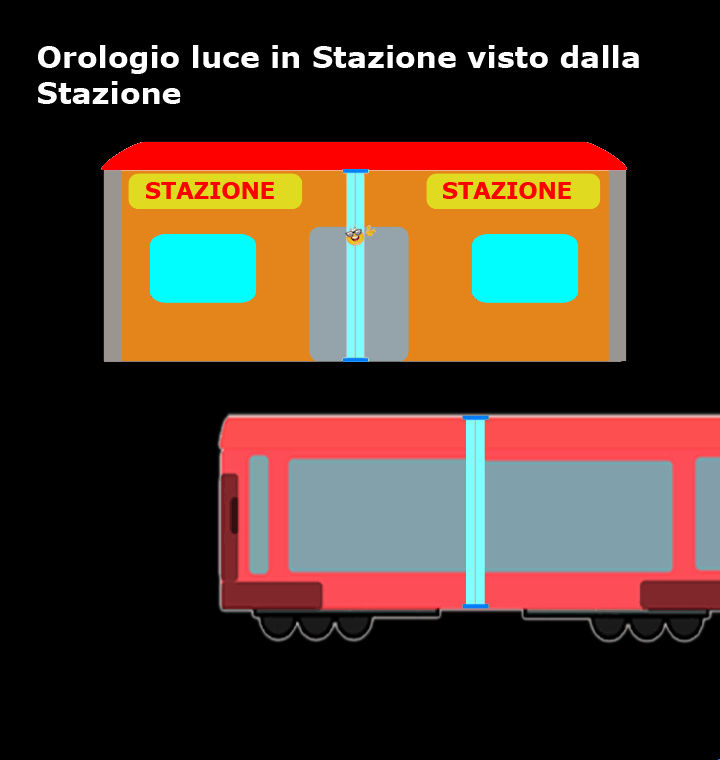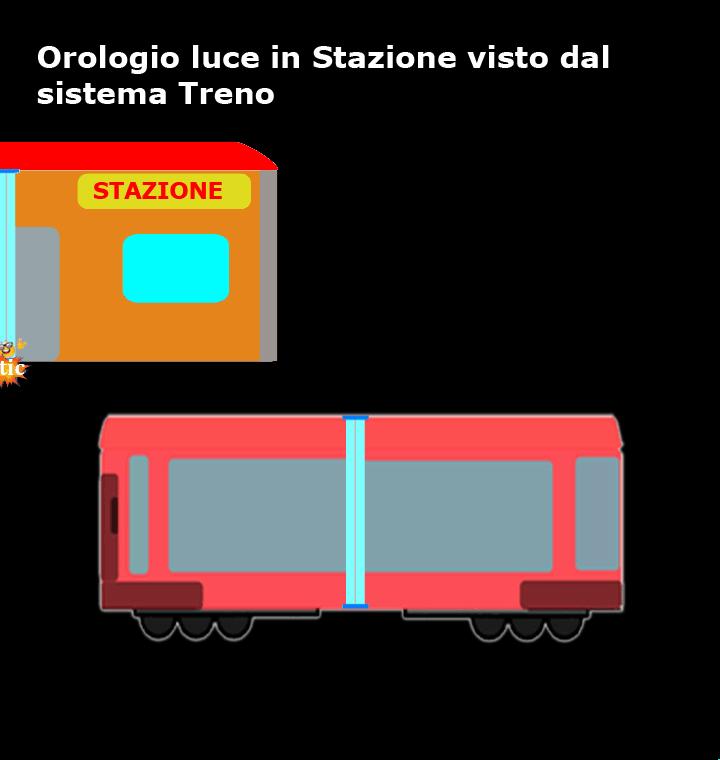
Come mostra questo breve filmato, per chi si trova sul treno l’orologio luce è fermo e il nostro amico fotone si muove verticalmente da uno specchio all’altro, mentre è la stazione che si muove.
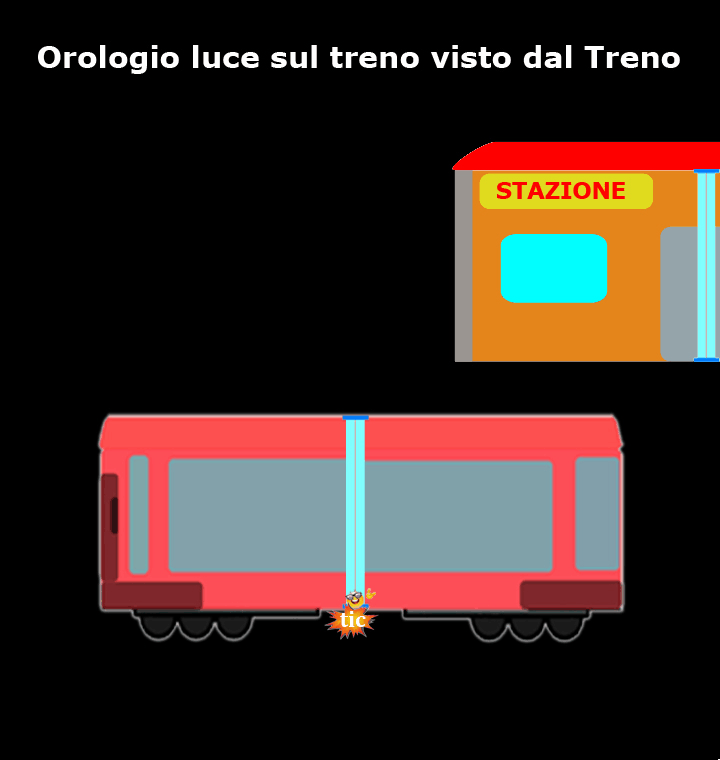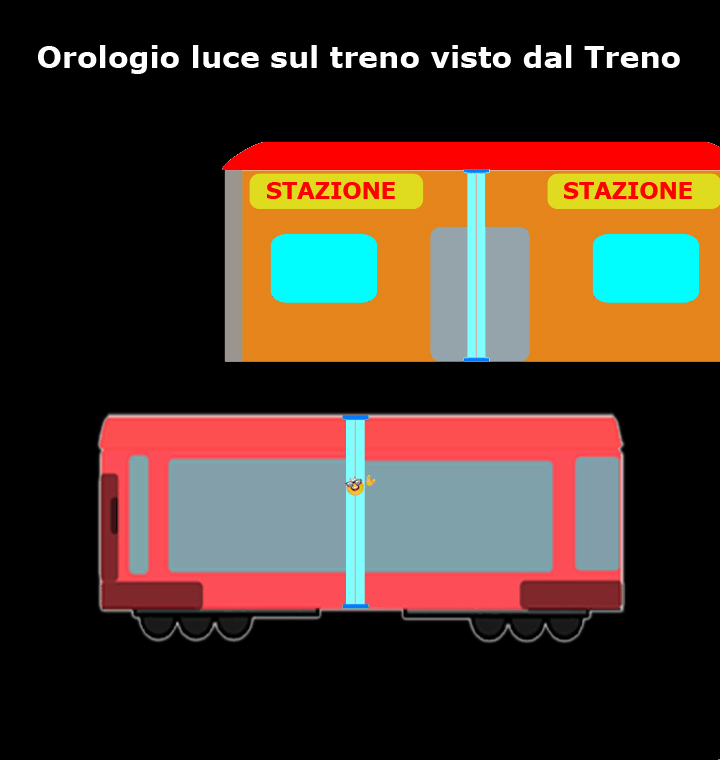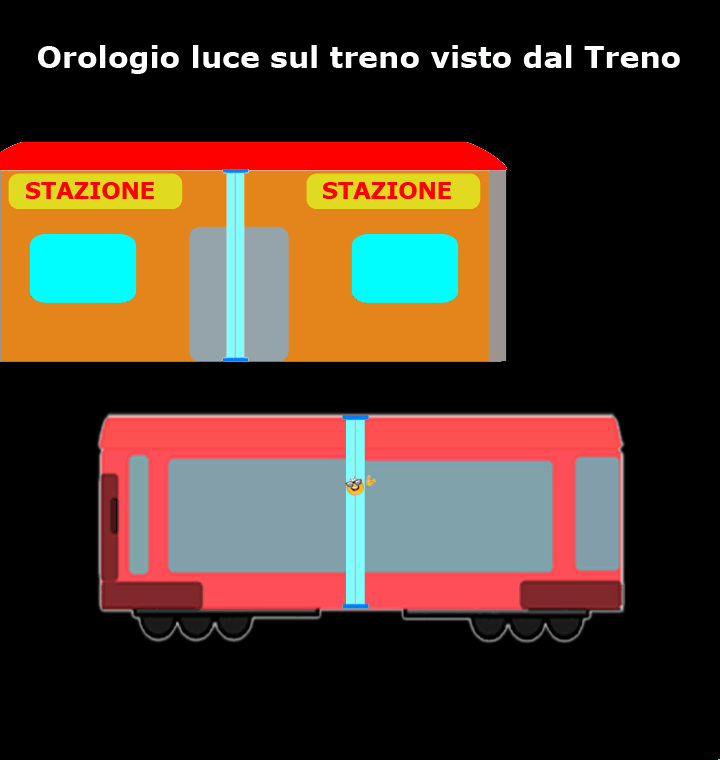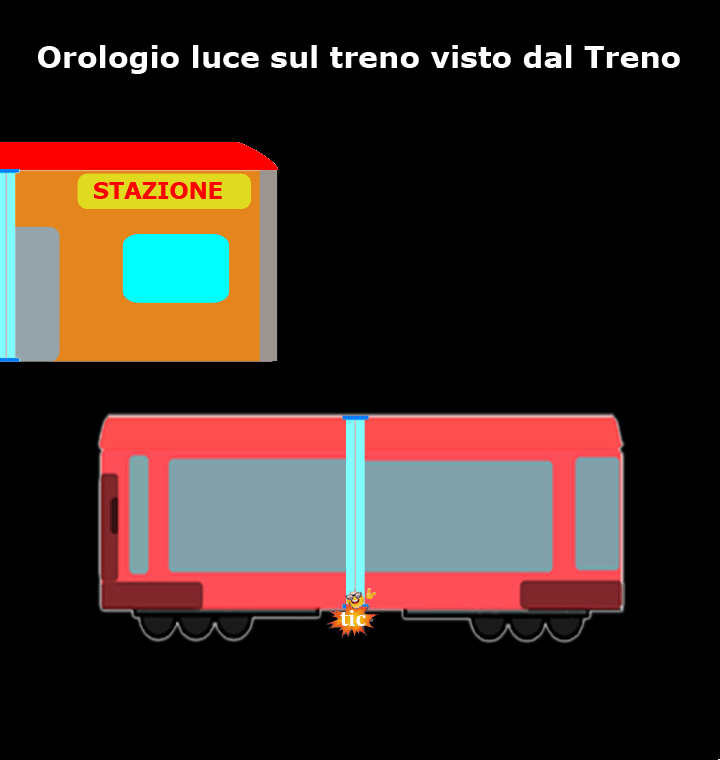
Per i passeggeri del treno quello è il loro sistema di riferimento inerziale, per cui loro ed il resto del treno sono fermi e sono la stazione ed il paesaggio che si muovono a velocità prossima a quella della luce (d’altronde questo è ciò che capita a chiunque guarda fuori dal finestrino di un treno).
Per non confondersi, lo scorrere del tempo misurato dai passeggeri del treno viene indicato con t’.
I passeggeri del treno confermano che l’orologio luce è preciso come promesso dai loro costruttori e la luce compie sempre lo stesso tragitto, da A a B e da B ad A, nel medesimo intervallo di tempo Δt’.
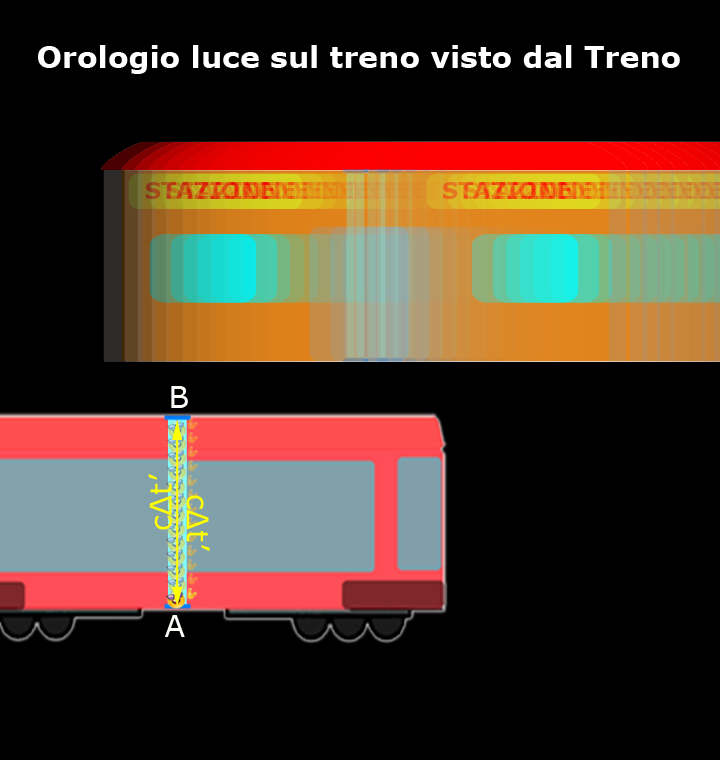
Dato che lo Spazio percorso è uguale alla velocità moltiplicata per il tempo (S = v Δt), il tragitto percorso dalla luce tra un tic e un tac, ossia per andare da A a B e da B ad A, ovviamente è uguale alla velocità della luce (c) moltiplicata per l’intervallo di tempo impiegato (Δt’):
AB = c Δt’
BA= c Δt’
I dubbisti presenti sul treno sono soddisfatti, il loro orologio funziona proprio come promesso.
La seconda fase dell’esperimento, però, consiste nell’analizzare dalla banchina della stazione il comportamento dell’orologio luce posto sul treno.
Accipicchia, come mostra questo breve filmato, per coloro che si trovano sulla banchina della stazione sono loro ad essere fermi, mentre il treno e l’orologio luce si muovono a velocità costante (in verso opposto rispetto a ciò che vedevano i passeggeri del treno) ed il percorso del nostro amico fotone, tra un tic e un tac, non è verticale, ma diagonale!
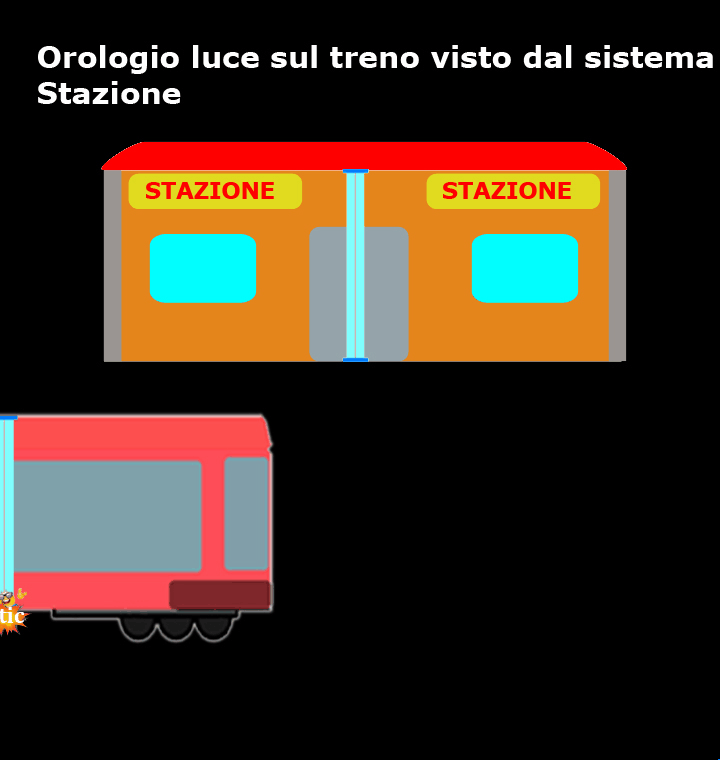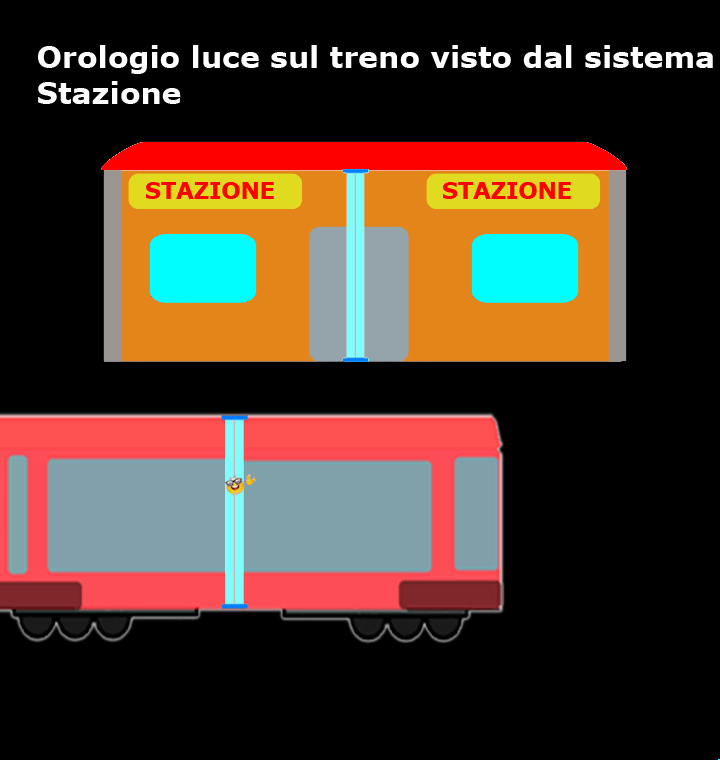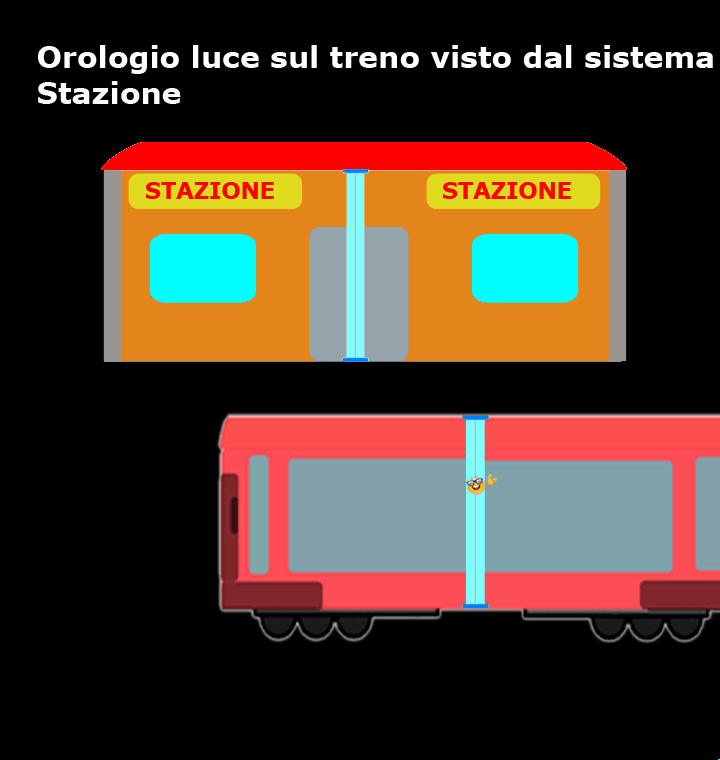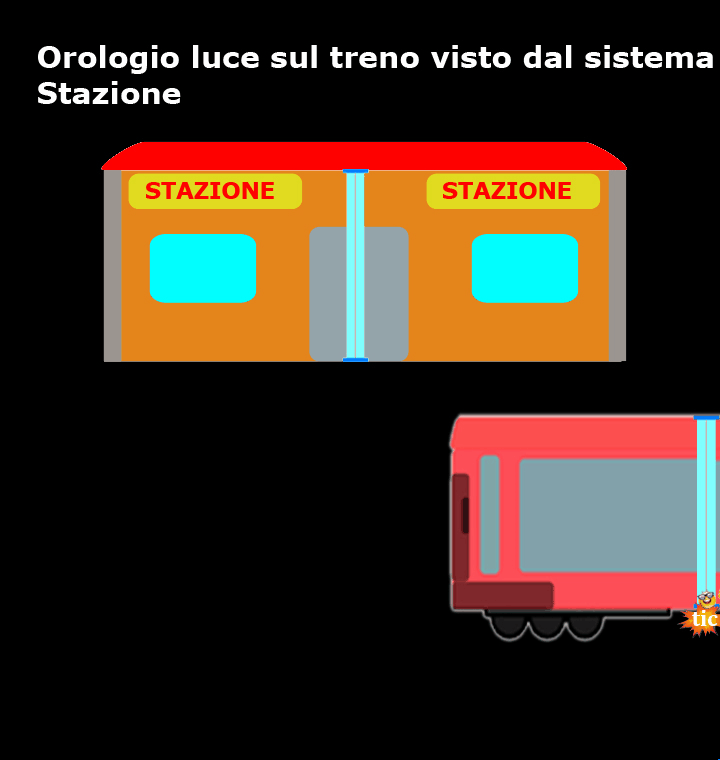
Rispetto a chi si trova sul treno, per chi si trova sulla banchina della stazione la luce ha sicuramente percorso uno spazio maggiore.
Ma se la velocità della luce è sempre la stessa e se lo spazio percorso, per chi si trova in stazione, è maggiore, allora anche il tempo impiegato deve essere maggiore.
Per non confondersi, lo scorrere del tempo misurato da chi si trova in stazione viene indicato con t.
I dubbisti che si trovano in stazione vedono il nostro amico fotone compiere sempre lo stesso tragitto, ma non nel breve tratto da A a B e da B ad A come quelli del treno, ma in un tratto più lungo da C a B e da B a D, come mostra la figura.
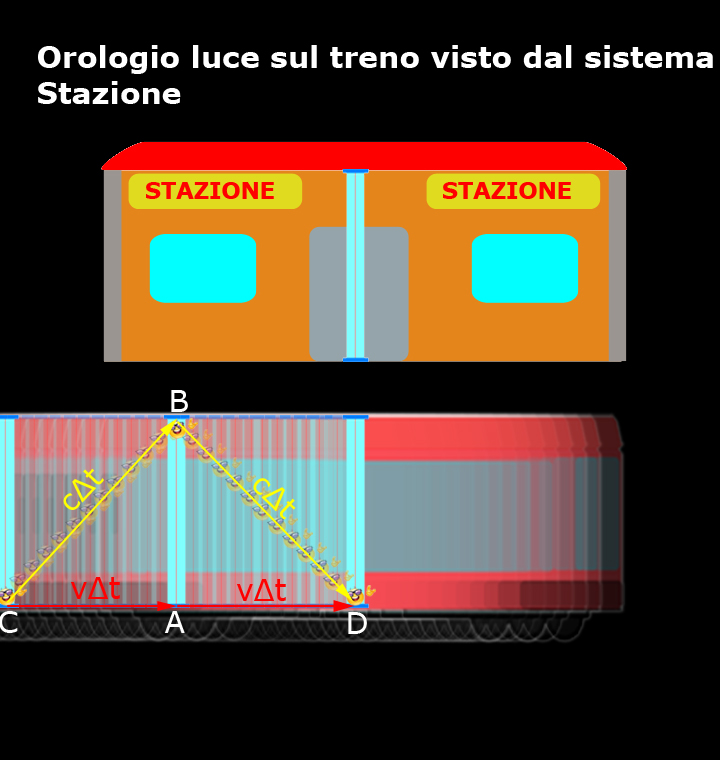
Per chi si trova in stazione il tragitto percorso dalla luce tra un tic e un tac, ossia per andare da C a B e da B a D, ovviamente è uguale alla velocità della luce (c) moltiplicata per l’intervallo di tempo impiegato (Δt):
CB = c Δt
BD = c Δt
Per chi si trova in stazione, nel medesimo intervallo di tempo (Δt) l’orologio luce si muove da C ad A e da A a D, alla velocità v, ossia alla velocità del treno misurata da chi si trova in stazione.
Pertanto è facile calcolare il tragitto percorso dal treno, ossia:
CA = vΔt
AD = v Δt
Dopo questa prova, alcuni dubbisti cominciano a dubitare sull’infallibilità dell’orologio luce, che visto dalla stazione sembra non funzionare più così precisamente, ma il problema non è l’orologio, ma come avevano avvertito i suoi costruttori è lo scorrere del tempo che può mutare passando da un sistema di riferimento (il treno) ad un altro (la stazione).
D’altronde se fosse la luce a mutare velocità, per chi si trova in stazione, il nostro amico fotone dovrebbe viaggiare più veloce della luce per compiere un tragitto più lungo (CB> AB e BD >BA) nel medesimo tempo.
Peccato, però che nulla può viaggiare più veloce della luce.
Cambiando sistema di riferimento inerziale, ossia passando dal treno alla stazione, l’orologio luce posto sul treno sembra scorrere più lentamente.
Basta confrontare le due visioni ed i rispettivi tragitti percorsi dalla luce per mostrare che il tempo misurato sul treno tra un tic e un tac (Δt’) è minore del tempo tra un tic e un tac (Δt) misurato dalla stazione.
E’ anche possibile calcolare di quanto rallenta il tempo del treno misurato dal sistema stazione, applicando semplicemente il Teorema di Pitagora, come mostra la figura seguente, dato che abbiamo a che fare con due identici triangoli rettangoli:

Quindi se per chi sta sul treno l’orologio luce tra un tic e un tac misura che è trascorso 1 secondo (Δt’ =1), per chi sta in stazione è trascorso più di 1 secondo (Δt > 1), ossia:
Δt’= Δt √(1- v²/c²)
1 = Δt √(1- v²/c²)
1/√(1- v²/c²) = Δt
Di quanto rallenta il tempo del treno misurato da chi sta in stazione, dipende dal rapporto tra la velocità del treno e quella della luce (v/c).
Non a caso il rapporto 1/√(1- v²/c²) è conosciuto in tutto l'universo come fattore di Lorentz (indicato come γ = 1/√(1- v²/c²)), poiché da questo dipende di quanto il tempo del treno misurato dalla stazione rallenta.
Se per esempio il treno visto dalla stazione viaggia al 60 % della velocità della luce, ossia v/c = 0,6, se sul treno è passato 1 secondo (Δt’ =1) in stazione sono trascorsi 1,25 secondi, dato che:
1/√(1- v²/c²) = Δt
1/√(1- 0,6²) = 1/√(1- 0,36) = 1/√0,64 = 1/0,8 = Δt
1,25 secondi = Δt
Dopo questa prova una parte dei dubitosi cominciano a pensare che l'orologio luce funziona correttamente solo sul treno, dimenticandosi che questa ipotesi è già stata scartata, poiché la velocità della luce nel vuoto è costante ed insuperabile, mentre un'altra parte pensa che per chi si muove velocemente il tempo rallenta.
Il fatto è che entrambi hanno torto!
Per dimostrarlo basta proseguire l'esperimento.
Ora l'orologio luce viene posizionato in stazione e per chi si trova sulla banchina l'orologio luce è fermo e il nostro amico fotone si muove verticalmente da uno specchio all’altro, mentre è il treno che si muove.
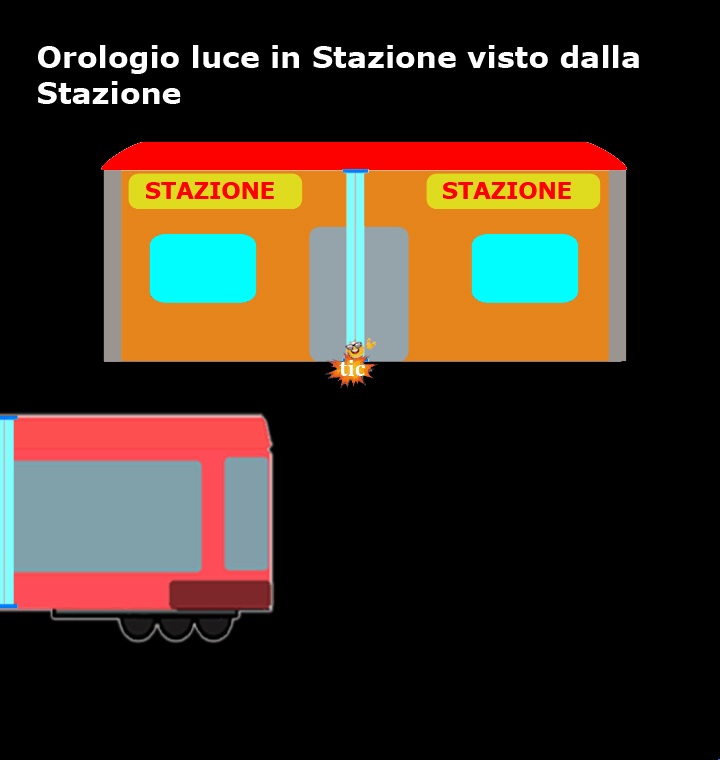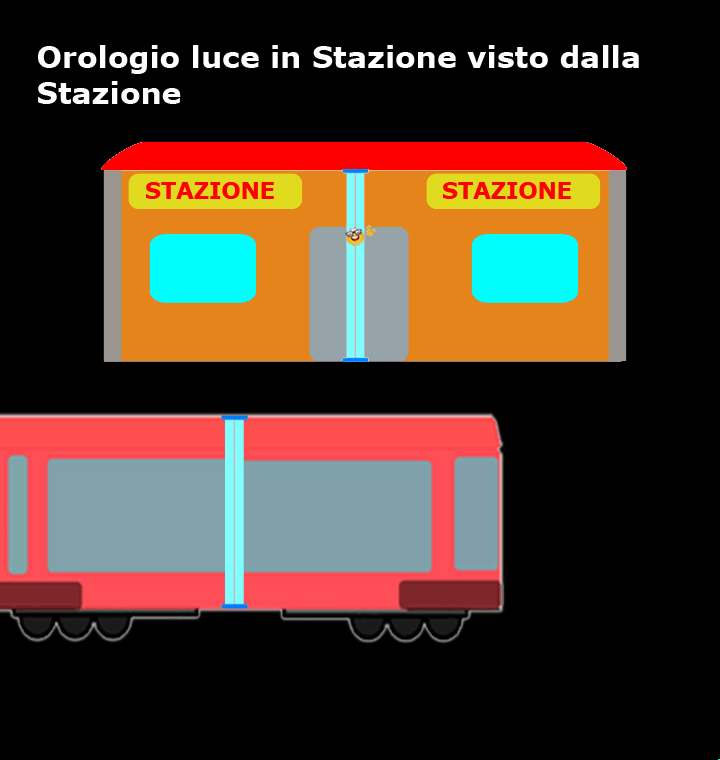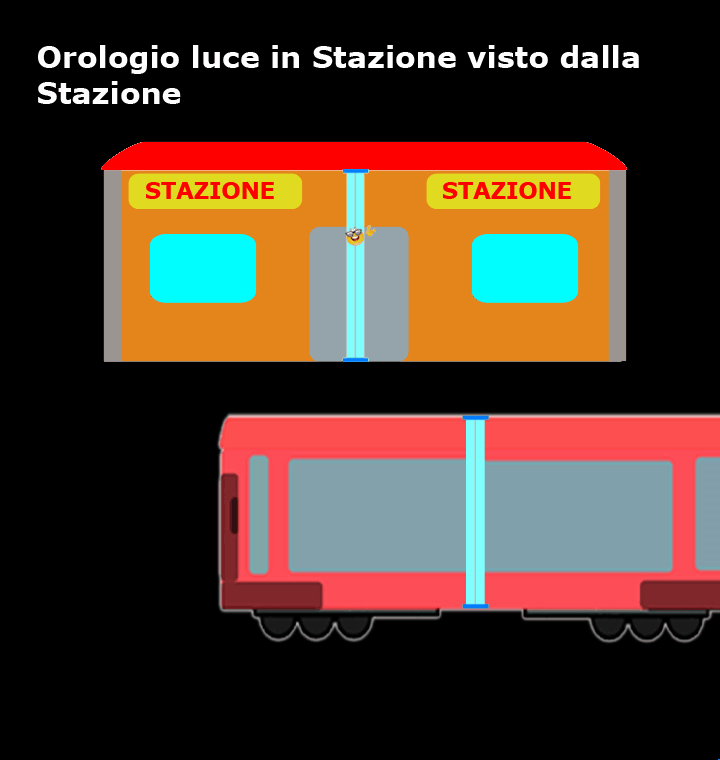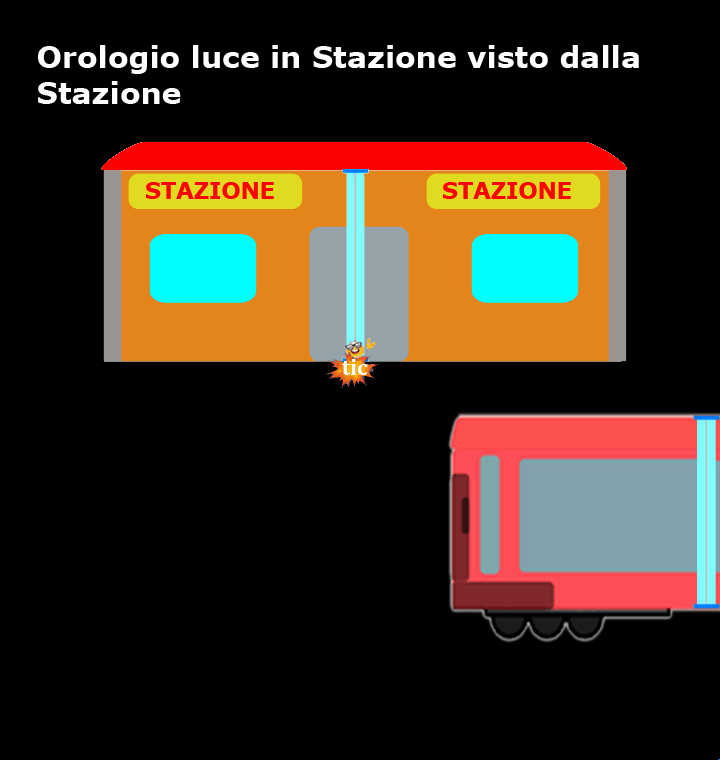
Ora, sono i dubbisti che si trovano in stazione a confermare che l’orologio luce è preciso come promesso dai loro costruttori e la luce compie sempre lo stesso tragitto, da A a B e da B ad A, nel medesimo intervallo di tempo Δt, pertanto:
AB = c Δt
BA = c Δt
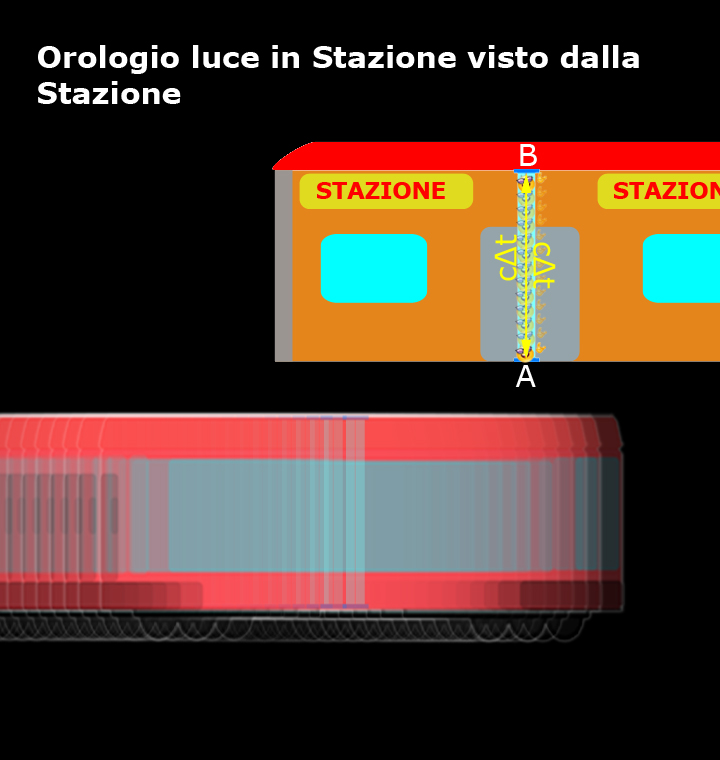
I dubbisti presenti in stazione sono soddisfatti, il loro orologio funziona proprio come promesso.
L'ultima fase dell’esperimento consiste nell’analizzare dal treno il comportamento dell’orologio luce posto in stazione.
Come mostra questo breve filmato, per coloro che si trovano sul treno sono loro ad essere fermi, mentre la stazione e l’orologio luce si muovono a velocità costante (in verso opposto rispetto a ciò che vedevano quelli che stavano in stazione) ed il percorso del nostro amico fotone, tra un tic e un tac, non è verticale, ma diagonale!
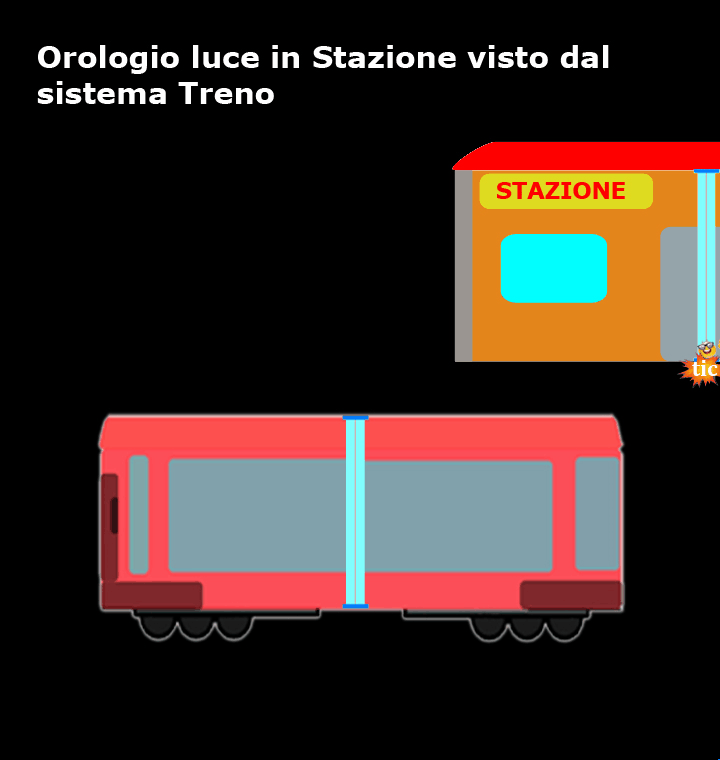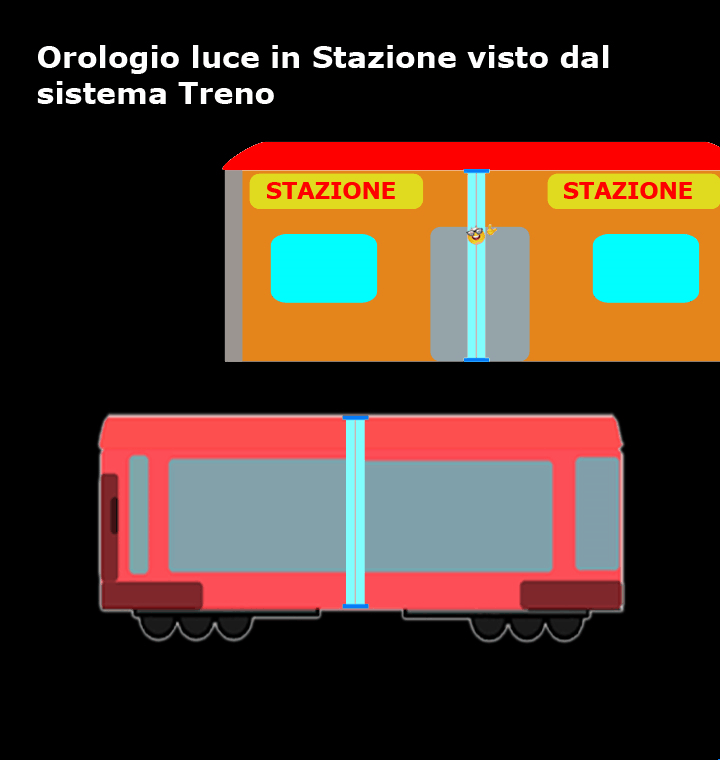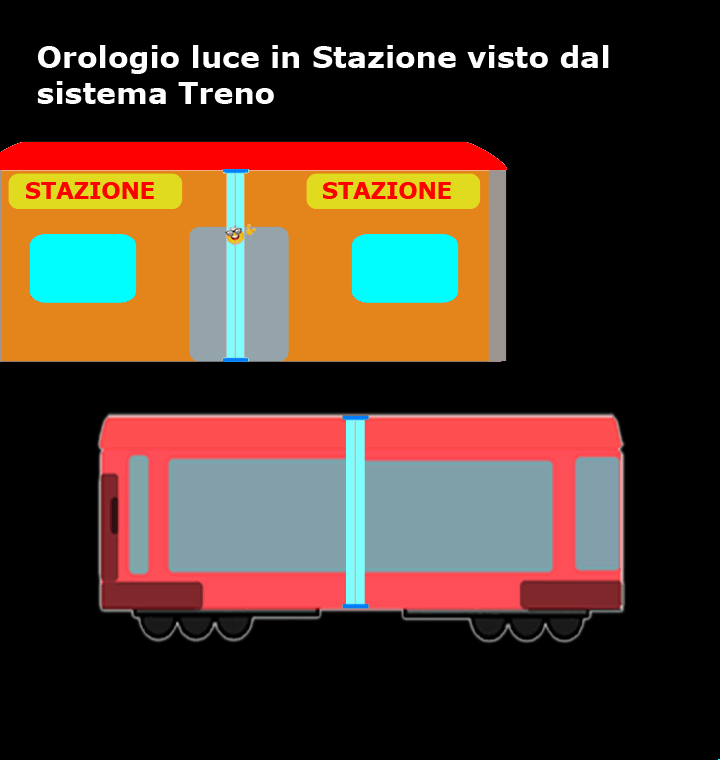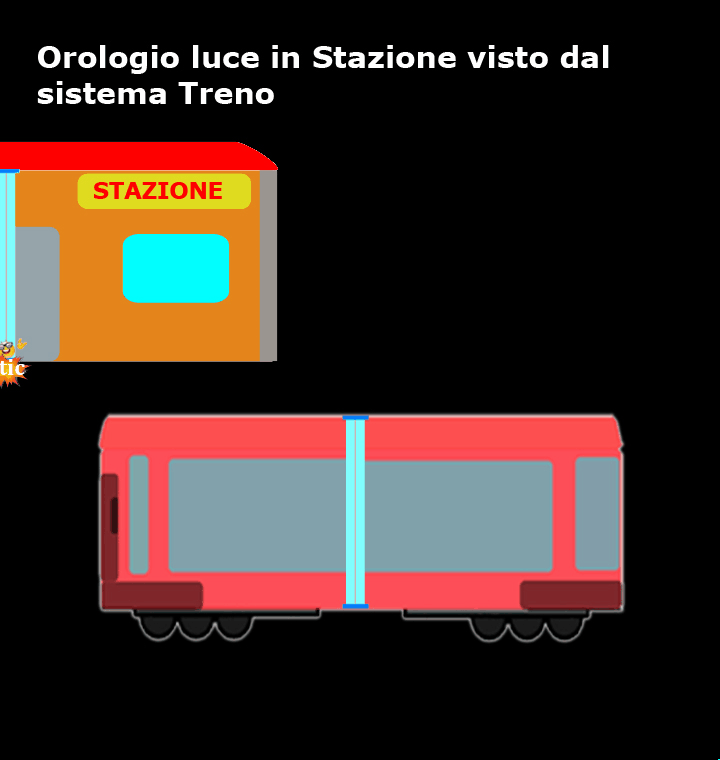
Rispetto a chi si trova in stazione, per chi si trova sul treno la luce ha sicuramente percorso uno spazio maggiore.
I passeggeri del treno vedono il nostro amico fotone compiere sempre lo stesso tragitto, ma non nel breve tratto da A a B e da B ad A come quelli della stazione, ma in un tratto più lungo da C a B e da B a D, come mostra la figura.
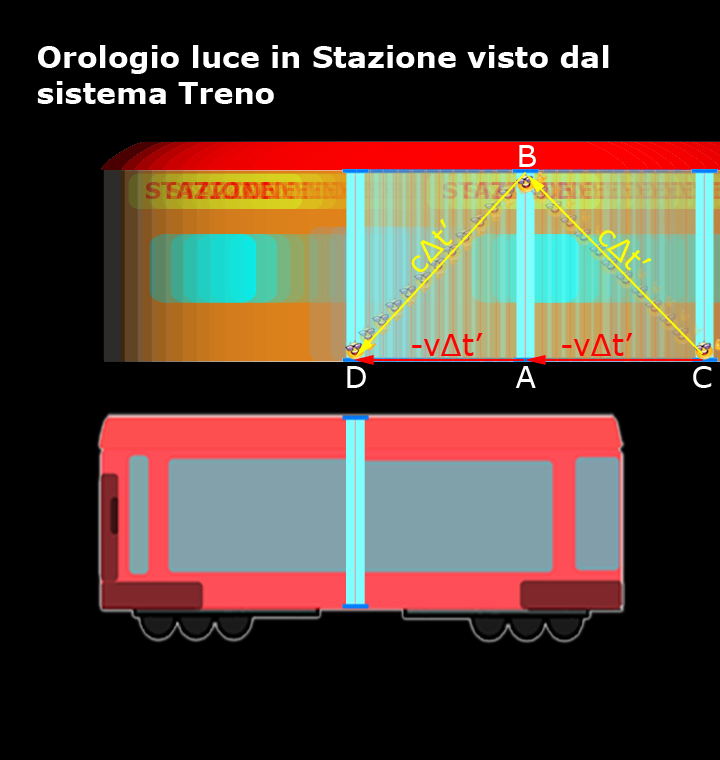
Di nuovo, come prima, ma nel verso opposto e nell'intervallo di tempo Δt' (quello del sistema treno) per chi si trova sul treno:
CB = c Δt'
BD = c Δt'
e nel medesimo intervallo di tempo (Δt') l’orologio luce si muove da C ad A e da A a D, alla velocità -v (il segno meno indica che è cambiato il verso della velocità), ossia alla velocità della stazione misurata da chi si trova sul treno, pertanto:
CA = -vΔt'
AD = -v Δt'
Proprio come prima, cambiando sistema di riferimento inerziale, l’orologio luce posto sull'altro sistema di riferimento (in questo caso la stazione) scorre più lentamente.
Basta confrontare le due visioni ed i rispettivi tragitti percorsi dalla luce per mostrare che il tempo misurato dalla stazione tra un tic e un tac (Δt) è minore del tempo tra un tic e un tac (Δt') misurato dal sistema Treno.

Ora è il tempo della stazione (Δt) che secondo il sistema di riferimento del treno scorre più lentamente:
Δt = Δt' √(1- v²/c²)
Anche i dubitosi più incalliti sono costretti ad ammettere che poco importa se l'orologio luce è sul treno, oppure in stazione, se lo si guarda dal suo sistema di riferimento tutto funziona perfettamente, mentre se si cerca di misurare il suo tempo da un altro sistema di riferimento, questo risulta rallentato.
Vi è una perfetta simmetria tra due sistemi di riferimento inerziali, poiché per chi sta in stazione è il tempo sul treno che scorre più lentamente, mentre per chi sta sul treno è il tempo della stazione che scorre più lentamente.
Questo bizzarro comportamento mostrato nell'esperimento non dipende certo dal tipo di orologio che si utilizza (si poteva anche confrontare l'età di due gemelli), semplicemente mostra che la misura del tempo, il suo scorrere, dipende dal proprio sistema di riferimento inerziale, al suo interno il tempo scorre come sempre, ma se si prova a confrontarlo con lo scorrere del tempo di un altro diverso sistema di riferimento inerziale, quest'ultimo risulta rallentato.... e se cambia il tempo è costretto a mutare anche lo spazio...
Questo articolo è stato inserito nella pagina d'archivio "La Relatività Ristretta per tutti" all'interno della sezione "Velocità della luce, Relatività e Buchi Neri".






19 commenti
ottimo, ma questo esempio necessita di ragionare in 2 dimensioni, mi piacerebbe vedere un esempio in 1 D , cioè con i due specchietti entrambi posizionati sul pavimento del treno in modo da escludere dimensioni "extra".
Caro Leandro, l'orologio luce è stato posto in verticale, poichè la sua altezza non cambia per nessuno dei due sistemi di riferimento (l'asse y è uguale per entrambi i sistemi di riferimento).
In questo modo, a mio avviso, è più semplice mostrare la diltazione del tempo.
Nella prossima puntata invece verrà posizionato in orizzontale, al fine di dimostrare che lungo la direzione del moto la lunghezza dell'orologio posto in un sistema considerato in moto, misurato da un sistema considerato in quiete, risulta contratta.
Ovviamente, come abbiamo appena dimostrato, poco importa se il sistema considerato in quiete è la stazione oppure il treno, così come è sempre il tempo dell'altro sistema a rallentare è sempre la lunghezza dell'altro sistema che risulta contratta.
Paolo
Per accontentare Leandro, propongo la mia versione messa in orizzontale...
Nel sistema in basso (fermo) esiste un orologio virtuale posto nella posizione indicata in T1. T1 è il tempo necessario perché la pallina arrivi in cima. Il sistema in moto (in alto) quando arriva in T1 non può far vedere la pallina in alto dato che lei non può andare più veloce di c. Ne consegue che la pallina è decisamente più indietro rispetto a quella del sistema fermo. Tutto ciò indipendentemente dal tempo proprio dell'orologio in movimento che non cambia per niente e rimane uguale a quello del sistema fermo.
Sono, però, convinto che usare l'orologio in verticale sia più comprensibile e anche più facilmente disegnabile...
Perfetto: è quello che intendevo. Infatti la pallina rimane indietro se vista dal sistema fermo, ma sommando l'effetto della contrazione della lunghezza, rimane meno indietro di quanto si pensi. Ragioniamo così : non sappiamo per adesso di quanto rimane indietro ma sicuramente possiamo dire che, per ogni lunghezza dell'orologio data , essa rimane indietro proporzionalmente alla lunghezza stessa. Poiché la lunghezza determina i tempi (proprio e non proprio) possiamo dire che, fissata una velocità di scorrimento, i tempi sono proporzionali. Questo giustifica pienamente il metodo della K di Bondi che in un baleno dimostra l'effetto doppler relativistico, le equazioni di Lorentz e il NON paradosso dei gemelli.
il calcolo k di Bondi è sicuramente un metodo rapido e istruttivo. Tuttavia, io no lo amo tanto dato che inserendo la luce nel discorso di invio e ricezione si perde un po' di vista il concetto di sistema di riferimento einsteniano. Sarò all'antica, ma preferisco l'orologio di luce. Però, chissà... potrebbe anche essere più facile a capirsi per i neofiti... non so...
Anzi, Leandro... così come abbiamo pubblicato Epstein, potresti occuparti di una esposizione semplificata del calcolo k. Se ne hai voglia e tempo sei il benvenuto...
Concordo con Enzo e provo a tradurlo in un'immagine: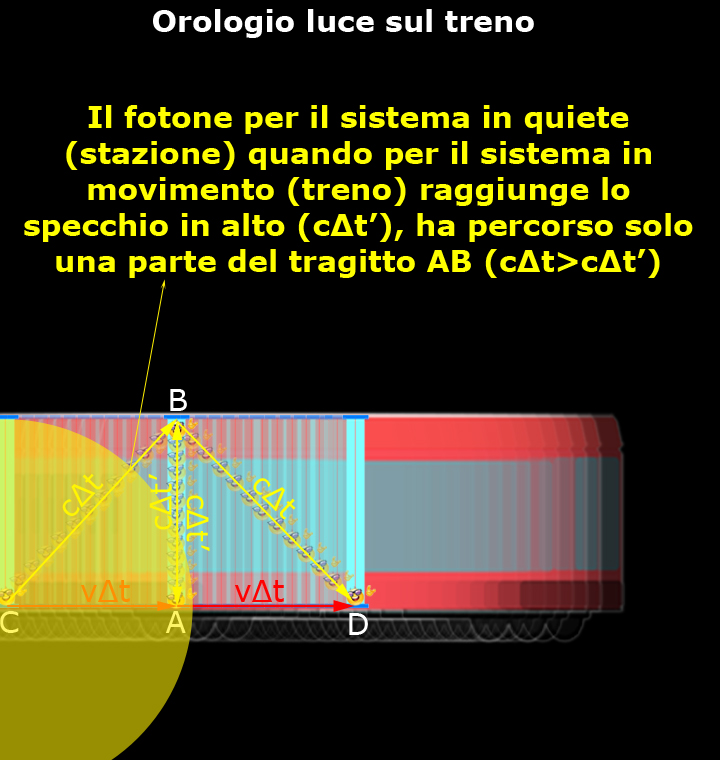
Il tempo del sistema considerato in movimento (Δt'), misurato dal sistema in quiete non può esser lo stesso, solo la velocità della luce è costante (il suo percorso CB è maggiore di AB), è il tempo del sistema considerato in movimento che rallenta (Δt' < Δt).
Paolo
Chiedo scusa mi sono accorto che la dicitura nella figura poteva creare confusione, per cui la ripropongo con un altra dicitura che mi sembra più chiara...
mi sono accorto che la dicitura nella figura poteva creare confusione, per cui la ripropongo con un altra dicitura che mi sembra più chiara...
Paolo
Veramente ben fatto. Un esempio davvero didattico. Il bello della RR è che la si può affrontare prendendo spunto da cose che accadono sotto gli occhi di tutti: basta un treno che passa in stazione e un po' d'immaginazione (neanche poi troppa). Ecco perchè sarebbe davvero utile e produttivo insegnarla nelle scuole. E in più insegna a fare i cosiddetti "esperimenti mentali", cosa su cui trovo che le menti dei ragazzi siano debolissime: faticano a "vedere" nella mente lo svolgersi dei fenomeni. E sì che di realtà virtuale ne mangiano a piacere! Potrei dire: la mangiano ma non la saprebbero cucinare...
Io farei in modo che le figure con il ritardo visibile del fotone a zig zag fossero messe in evidenza se no si rischia di pensare a una figura come quella di Arturo poi tolta e corretta...
E' per questo che ho preferito fare la mia figura 12. Come detto ad Arturo si dovrebbero mettere a fianco le animazioni con il zig zag galileiano e relativistico. Salterebbe subito all'occhio il ritardo della seconda "pallina" e tempi propri e impropri si capirebbero ancora meglio... io non sono capace a creare animazioni, ma Arturo le farà sicuramente...
il testo finale dovrebbe avere incorporate anche molte animazioni per quanto possibile...
Prendiamo il caso dell’orologio luce sul treno in corsa. Io dico che qui i nostri amici fotoni compiono ancora i tratti AB e BA e non CB e BD. Supponiamo che sul vagone vi sia piantata una pertica di cinque metri dal pavimento al soffitto e io, toltimi settant’anni, mi debba arrampicare fino in cima. Lo farò sempre con cinque bracciate e sempre per quella via proprio come se il treno fosse fermo. E ancora, se questa volta sul solito treno in corsa, una formica dal pavimento raggiungesse il soffitto camminando lungo la pertica, a nessuno verrebbe mai in mente di dire che ha percorso nello spazio una linea immaginaria che va dal punto in cui si trovava la base della pertica alla partenza, fino al punto in cui si trova all’arrivo sul soffitto. Non vedo perciò come io e la formichina si debba rallentare nella salita perché il treno è in corsa.
Per rispondere alla tua obiezione forse è meglio precisare due cose.
La prima è che per ogni sistema di riferimento (il treno o la stazione) il proprio tempo scorre come sempre.
Pertanto, all’interno del proprio sistema di riferimento l’orologio luce funziona come sempre (la luce va da A a B e da B ad A) ed il tempo scorre come sempre.
Se invece si prova a misurare il tempo di un diverso sistema di rifermento inerziale, usando molti orologi (ossia il mio sistema di riferimento temporale), il tempo dell’altro sistema di riferimento scorre più lentamente di quello misurato dal mio.
Per esempio, nel caso dell’orologio luce sul treno, per chi sta in stazione la luce va da C a B e da B a D (ossia compie un tragitto più lungo) ed il tempo del sistema treno risulta scorrere più lentamente di quello del sistema stazione (tempo orologi stazione > tempo orologio luce sul treno).
La seconda questione è che la velocità della luce è uguale per qualunque sistema di riferimento, pertanto non posso sommare (vettorialmente) come faceva Galileo alla velocità della luce la velocità del treno, poiché si otterrebbe una velocità maggiore di quella della luce (cosa impossibile).
Non a caso per confrontare i tempi di due sistemi di riferimento è stato usato un orologio luce e non un orologio a formica … la velocità della luce è uguale per entrambi i sistemi di riferimento, pertanto a cambiare è la misura del tempo e dello spazio, o meglio per ogni sistema di riferimento inerziale il tempo di un altro sistema di riferimento inerziale risulta dilatato e lo spazio contratto.
Paolo
Premetto che non ho nessuna base formativa di fisica perché non l’ho mai studiata. Ciononostante mi piace la materia e mi trovo a leggere in rete tutto ciò che tratta l’argomento della dilatazione del tempo e della contrazione delle lunghezze. Tralascerei tutti gli esperimenti che ne danno la prova perché questi accertano solo i fatti ma non dicono mai il motivo per cui si verificano ed è appunto questo che a me interessa. Mi soffermerei per esempio sull’orologio luce di Einstein. Secondo me quando l’apparato è in movimento l’orologio non funziona perché il fotone non raggiunge più lo specchio in alto. Io credo che questo corpuscolo debba proseguire lungo la verticale sul punto dello spazio in cui si trovava il generatore quando l’ha emesso, altrimenti mi chiedo quale sia la forza esatta che lo spinge a rincorrere e raggiungere lo specchio che gli sfugge. Però poi ammetto che ci deve essere qualcosa che a me sfugge e sarei grato se mi si dicesse cos’è.
La risposta potrebbe essere lapidaria; perché uno dei postulati della relatività è proprio che un fenomeno fisico si deve ripetere tale e quale in qualsiasi sistema inerziale. Da cui segue che se la luce colpisce lo specchietto in un sistema, lo deve fare in tutti gli altri. Da un punto di vista più "pratico" possiamo pensare alla luce come un'onda che si propaga e, quindi, ci sarà sempre un raggio di luce che colpirà lo specchietto anche spostato.
Infine, ricordiamoci anche (vedi aberrazione astronomica) che una cosa è non poter sommare le intensità delle velocità e un'altra cosa è la direzione di provenienza... la luce non può sommarsi, ma la sua direzione può cambiare...
Salve, ho difficolta' ad immaginare l'orologio di luce montato su un oggetto in movimento. Mi spiego.
Se la luce dell'orologio compie un percorso verticale oscillatorio continuo, ed il treno si muove in orizzontale costante, nella mia immaginazione la luce dovrebbe "uscire" dagli specchietti prima o poi, poiche', nel caso della luce, la componente orizzontale della velocita' del treno non si somma alla componente verticale della velocita' della luce. Quindi non capisco perche' si parli di un percorso "diagonale" (come se fosse una pallina di ping-pong dove in fatti le componenti delle velocita' verticale e orizzontale si sommano).
La cosa invece non mi "disturba" se l'orologio lo immagino montato su un oggetto fermo.
Capisco che tutto cio' e' contrario all'invarianza dei sistemi di riferimento, quindi penso di sbagliare nel ragionamento.
Potrebbe aiutarmi a capire dove sbaglio nel ragionamento?
P.S. Pensare alla luce come un onda non mi aiuta a capire, il postulato nemmeno e pensare alla luce che "cambia direzione" mi confonde ancora di piu'.
Non so se ho capito bene la sua obiezione.
Se l’orologio luce è montato sul treno, per chi sta nel vagone gli specchi non si muovono e la luce viaggia solo in verticale. D’altronde si parla di sistemi di riferimento inerziali, perciò per chi sta sul treno lui è fermo ed è il paesaggio si muove.
Per chi si trova a terra, invece gli specchi si muovono, eccome, mentre lui si ritiene fermo.
Ovviamente il fenomeno fisico della luce che rimbalza da uno specchio all’altro avviene per entrambi i sistemi di riferimento, solo che non coincidono i tempi.
Infatti per chi si trova a terra, la luce per raggiungere l’altro specchio compie un tragitto diagonale, non perché la luce si sommi alla velocità del treno, ma perché gli specchi si sono spostati e questo pe r chi è a terra è l’unico tragitto che consente alla luce di rimbalzare da uno specchio all’altro mentre questi si muovono.
caro Gianni,
ci sarebbero molti modi per spiegare la faccenda. Te ne cito tre... Il primo -e il più banale- è il rispetto delle leggi fisiche: un fenomeno che capita in un sistema di riferimento deve capitare tale e quale in qualsiasi altro sistema di riferimento. Se la luce colpisce lo specchio per chi sta sul treno lo deve fare anche per chi vede il tutto da terra.
Il secondo può essere proprio relativo all'onda che lascia la sorgente luminosa: essa si allarga a semicerchio e colpisce qualsiasi punto anche se in tempi diversi (come dice Paolo).
Il terzo è legato al diagramma di Minkowski: La luce viaggia sempre a 45° in qualsiasi sistema di riferimento. L'asse del tempo e dello spazio sono però inclinati rispetto a quelli di chi sta fermo. Basta fare la figurina e si vede subito che i tempi non coincidono (relatività della simultaneità), ma lo specchietto è sempre e comunque colpito.
Puoi vedere qui:
http://www.infinitoteatrodelcosmo.it/2015/10/01/lo-spaziotempo-di-minkowski-luniverso-in-un-foglio/
Ieri sera ho lasciato un commento che è stato regolarmente acquisito, infatti rientrando nel sito ho visto che era presente con la data e l'ora dell'inserimento.
Stamattina però il mio commento è scomparso, come mai?
Ripropongo adesso il commento fatto in precedenza, in maniera più sintetica, ma riferendolo sempre all'anno 1900 in modo da svincolarlo completamente dalle previsioni della Teoria della Relatività Ristretta di Einstein.
Credo che se fosse vissuto in quel periodo neanche il prof. Zappalà, libero dai condizionamenti di cui sopra, avrebbe risolto il problema dell'incompatibilità tra la costanza della velocità della luce "c" e le diverse distanze percorse da essa nei due sistemi inerziali "Treno" e "Stazione", ipotizzando che il tempo scorresse in maniera differente per essi.
Probabilmente avrebbe cercato altre soluzioni.
Secondo me la soluzione naturale , ed anche quindi la più semplice, è quella di ammettere che la luce, percorrendo una distanza maggiore nel sistema di riferimento "Stazione" abbia viaggiato ad una velocità maggiore di "c".
Questa affermazione potrebbe sembrare in contrasto con le evidenze sperimentali che confermano che la luce viaggia sempre alla stessa velocità "c", cosa di cui sono anch'io assolutamente convinto, ma di fatto non lo é in quanto la costanza di "c" va sempre riferita ad un osservatore e non ad un qualsiasi sistema di riferimento.
Nell'articolo sugli orologi luce l'individuo che si trova fermo in stazione non può vedere il raggio di luce nel primo tratto del suo percorso, quello obliquo tra i due specchi, pertanto non può essere considerato "osservatore" e quindi per lui la luce può viaggiare a velocità diversa da "c", nel nostro caso maggiore di "c".
Egli diventa "osservatore" nel momento in cui la luce colpisce lo specchio che diventa per lui "sorgente" e quindi in questo caso vedrà la luce viaggiare verso di lui esattamente alla velocità "c".