Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica.

Un problema classico che vale, però, la pena di richiamare: calcolare il punto di caduta di una particella lasciata libera di scivolare su una sfera di raggio R (fissata al suolo) sotto l’effetto della sola gravità terrestre. Un giochino  che non è del tutto intuitivo.

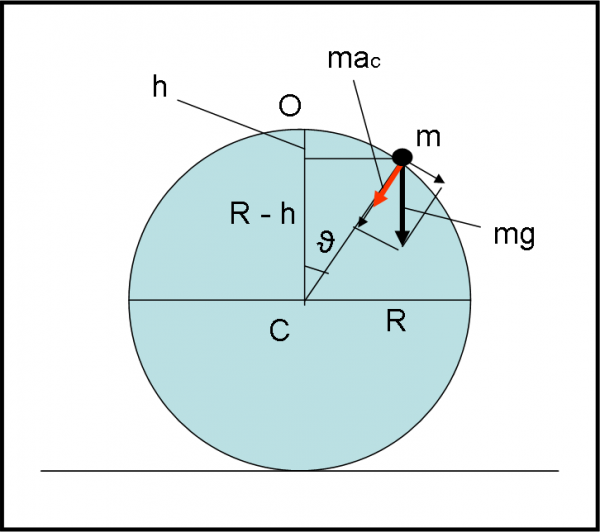
La Figura illustra ogni passaggio necessario al problema.

Analizziamolo, cominciando a definire le forze a cui è soggetta la particella di massa m. Essa subisce la gravità della Terra e questa forza è diretta verso il basso. L’accelerazione  la chiamiamo, ovviamente g.

F_g = m g

Inoltre, la particella si nuove di moto circolare attorno al centro C della sfera e subisce una forza centripeta che vale:

F_c = m a_c

La prima forza è diretta verso il basso, mentre la seconda è diretta verso il centro della sfera.

La forza di gravità può essere scomposta in due componenti: una tangente alla sfera e una diretta verso il centro. Basta un po’ di trigonometria banale per trovare che la componente radiale, F_gR, diretta verso il centro, è data da:

F_gR= m g cosϑ

Cosa tiene la particella a contatto della sfera è la risultante delle forze che agiscono in senso radiale. La componente tangenziale (dovuta solo alla gravità) è proprio quella che vuole farla scappare per la tangente.

In altre parole, chi comanda è la differenza:

mg cosϑ – ma_c

La particella se ne va per la tangente quando:

mg cosϑ – ma_c = 0

Ossia:

g cosϑ = a_c

E, ancora:

cosϑ = a_c/g    …. (1)

La massa m della particella è già scomparsa e ciò vuol dire che poteva essere qualsiasi. Comunque resta ancora g che è legata strettamente alla massa della Terra.

Non ci resta che utilizzare la solita conservazione dell’energia del sistema. L’energia totale è data dalla somma dell'energia potenziale e dell'energia cinetica:

E = E_cin + E_pot

Prima che la particella si muova l’energia è solo potenziale:

E = 0 + E_pot = mgh

Quando la particella se ne va per la tangente, l’energia è solo cinetica:

E = E_cin + 0 = ½mv²

Ma l’energia si deve conservare, perciò:

½mv² = mgh

Ossia

v² = 2gh  …. (2)

Sappiamo però dalla cinematica del moto circolare che:

a_c = v²/R    (l’abbiamo già ricavata varie volte)

Andiamo a sostituire questo valore nell’espressione del coseno (1)

cosϑ = a_c/g = v²/Rg

La (2) ci regala il valore di v² e, sostituendo, si ha:

cosϑ = 2gh/Rg = 2h/R    …. (3)

Accidenti, è sparita anche l’accelerazione di gravità e, quindi, la massa della Terra…

Proseguiamo…

Un po’ di geometria ci dice immediatamente che:

cosϑ = (R–h)/R

La (3) diventa:

(R–h)/R = 2h/R

E, infine:

h = R/3

Abbiamo trovato che la particella lascia la sfera sempre nello stesso punto, indipendentemente dalla massa della pallina e dalla massa della Terra. Tutto dipende solo dal raggio della sfera.

Potete sempre provare a casa…