I due fratelli (Pippo e Pappo), ormai ben noti, eseguono un interessante "lancio della ciliegia" e poi chiedono alla sorella Peppa di descriverne i risultati. Un modo relativamente semplice per fare il punto sui sistemi di riferimento senza utilizzare formule complicate.

Pappo sale su una piattaforma girevole P, mentre Pippo sta fuori di essa con le ciliegie, private del nocciolo. La situazione è quella di Fig. 1. All’inizio, la piattaforma è immobile e Pippo lancia direttamente le ciliegie verso Pappo che deve prenderle con la bocca. Dopo molti esercizi, i due fratelli sono ormai diventati dei veri campioni, sia nel lanciare che nel ricevere.

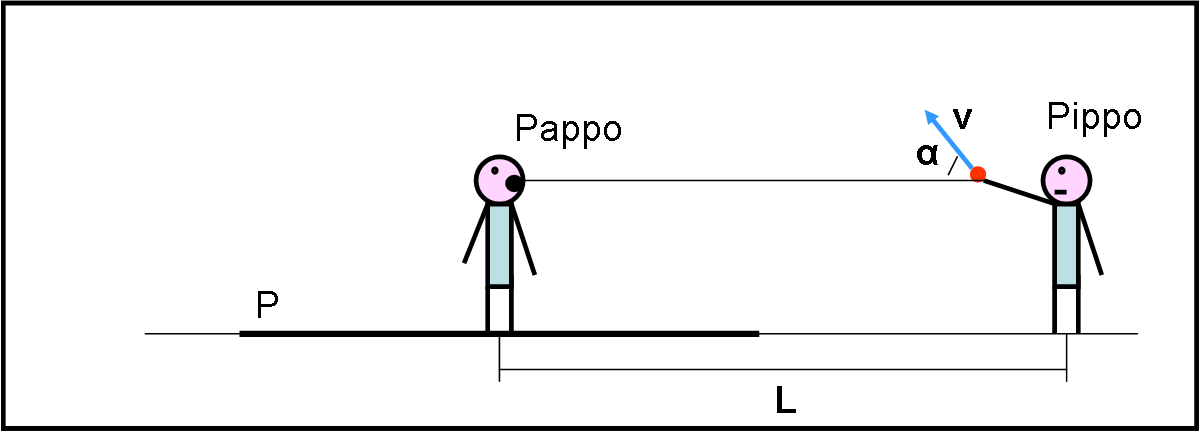
Vediamo le condizioni del gioco. Pippo lancia le ciliegie con una velocità v, che forma un certo angolo α con la linea orizzontale che unisce mano di Pippo e bocca di Pappo. La velocità è contenuta nel piano verticale rispetto al suolo e  la traiettoria è studiata in modo che il punto finale sia proprio la bocca di Pappo. La distanza tra i due fratelli è L.

Nel frattempo, è sopraggiunta Peppa, la sorella minore, un piccolo genio in geometria, che, però,  non ha ancora studiato la fisica a scuola e quindi ragiona in modo molto empirico, ma veramente brillante. Conosce solo la forza di gravità, un poco di scomposizione di vettori e si azzarda a calcolare il seno e coseno di un angolo, poco di più…

I fratelli le chiedono di DISEGNARE la traiettoria della ciliegia, vista sia nel sistema di riferimento di Pippo sia in quello di Pappo. Peppa si sente presa un po’ in giro e risolve immediatamente il problemino sia visto nel piano verticale che in quello orizzontale (ossia in quello della figura e in quello perpendicolare (visione dall’alto)) consegnando i quattro disegni veramente banali.

Abbastanza offesa, chiede ai due ragazzi di complicare un po’ la faccenda in modo da poter dimostrare la sua capacità grafica.

Pippo e Pappo confabulano a lungo e poi prendono la decisione con un bel sogghigno sul volto. L’ha voluto più difficile? e tale l’avrà!

Pappo torna sulla piattaforma girevole e, questa volta, la mette in moto con una velocità angolare costante ω. La velocità è tale che Pappo eseguirà due volte un giro completo prima di ripresentarsi frontalmente a Pippo, dopo un tempo τ, tale che la ciliegia arrivi esattamente nella bocca di Pippo. La velocità di lancio rimane esattamente la stessa della volta precedente (Fig. 2).

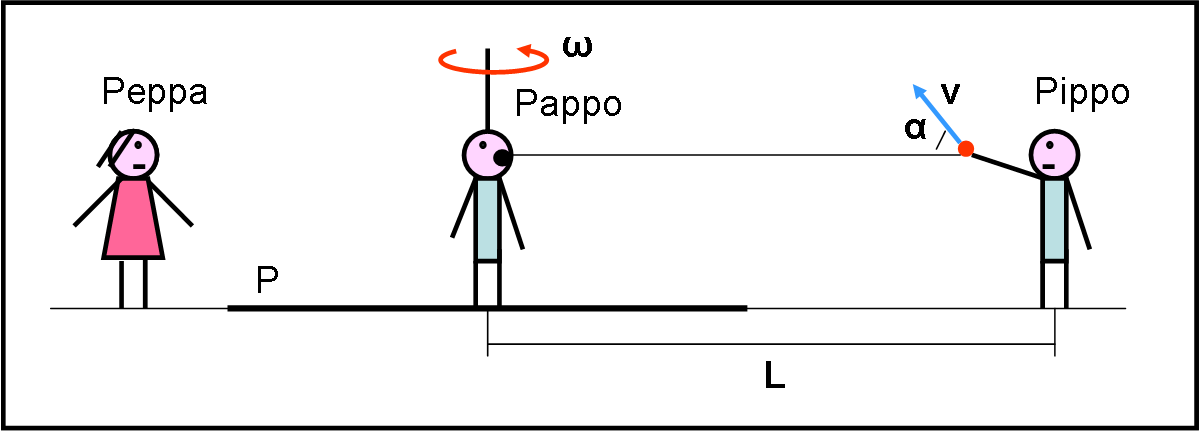
Per dare a Peppa un piccolo aiuto fanno un lancio di prova che riesce perfettamente. La bimba, però, nemmeno lo guarda ed è già completamente presa dal suo disegno. Pippo rimane un po’ sgomento, ma le rivolge lo stesso la domanda: “Disegna la traiettoria della ciliegia sia nel mio sistema di riferimento sia in quello di Pappo. La traiettoria deve anche essere rappresentata sia nel piano orizzontale sia in quello verticale”. Il suo sogghigno sparisce velocemente e si trasforma in meraviglia quando, dopo pochi minuti, Peppa presenta i quattro disegni ai due fratelli.

Tutto è perfetto, anche se la traiettoria è eseguita a mano libera e quindi non è molto accurata. Tuttavia, Peppa ha avuto l’accortezza di riportare i valori di distanza e di altezza della ciliegia in alcuni punti fondamentali della traiettoria.

Ovviamente, non si chiede nessuna legge del moto e nessun programma predisposto. Non c’è nemmeno bisogno di introdurre masse, forze vere o … apparenti. Una risposta puramente grafica legata ai dati del problema.

Peppa non ha ancora molte nozioni di matematica e geometria, ma si accorge di poter fare uno schizzo abbastanza buono senza bisogno di fare considerazioni troppo elevate per lei. Si affida, perciò, all’unica cosa di cui è sicura: la traiettoria vista dal riferimento esterno (Pippo), così come quella vista da Pappo con la piattaforma ferma, deve essere una parabola. E quella la sa disegnare (conoscendo l’accelerazione di gravità g e sapendo come scomporre il vettore velocità)! Ovviamente la parabola vista dall'alto diventa una retta per entrambi i sistemi.

Il problema rimane quello di disegnare la traiettoria nel sistema di riferimento rotante. Ovviamente, per il sistema di Pippo, nulla cambia: la ciliegia percorre la stessa traiettoria parabolica precedente. C’è anche da dire che questa curva rimane sempre valida e ciò che cambia e l’apparenza che essa viene ad avere nel sistema rotante. Il fenomeno fisico deve, comunque, essere lo stesso: la ciliegia parte da Pippo e arriva in bocca a Pappo.

La parabola, dovendo partire e arrivare alla stessa altezza deve avere il suo massimo in L/2 e dopo un tempo τ/2.

Tuttavia sappiamo, anche, che τ = 2T, dove T è il periodo che Pappo impiega a effettuare una rotazione.

Peppa disegna allora la traiettoria di Pippo rispetto a Pappo considerato FERMO. Essa non è altro che una circonferenza di raggio L (Fig. 1, in basso) ed è percorsa in senso orario con velocità angolare

ω = 2π/T

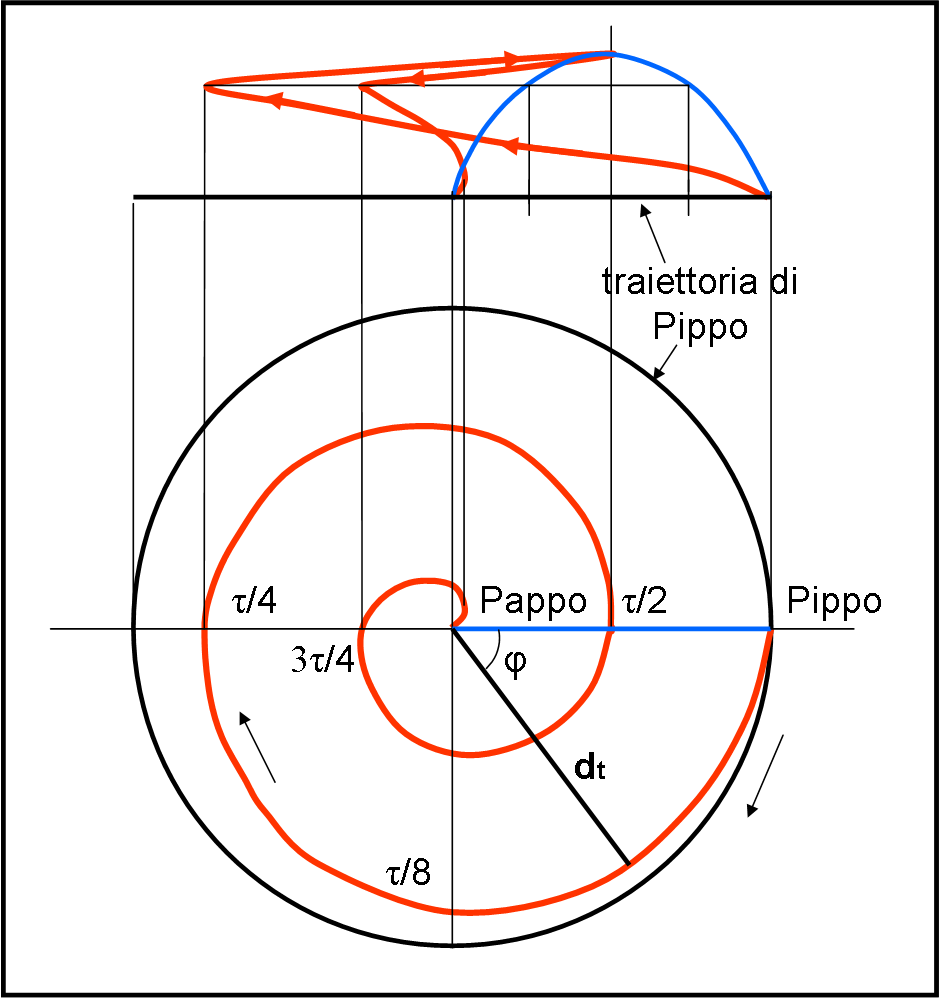
La rotazione angolare è costante, perciò vale anche la relazione (φ è l’angolo percorso da Pippo e anche dalla ciliegia che si muove SEMPRE nel piano perpendicolare alla congiungente Pappo-Pippo, ):

ω = φ/t

φ = ω t

φ = 2π t/T

φ = 4π t/τ         …. (1)    (dato che T = τ/2)

E perciò facilissimo ricavare l’angolo φ relativo al tempo desiderato

Ovviamente, per t = 0, φ = 0

Prendiamo qualche tempo particolare (ma potremmo calcolarne molti di più)

t = τ/8

φ = 4π t/τ = 4π τ/(8τ)

φ = π/2

Abbiamo l’angolo di posizione, ma ci manca la distanza della ciliegia da Pappo…

Tuttavia, se vogliamo disegnare ciò che avviene nel piano orizzontale (quello che contiene la piattaforma), sappiamo che il moto della ciliegia è un moto rettilineo uniforme. In poche parole, la componente della velocità lungo la direzione Pappo-Pippo è sempre la stessa per tutto il tempo τ. Chiamiamo questa velocità costante v_r (ma ci importa poco il suo valore). Chiamiamo, anche, L_t la distanza contata a partire da Pippo, dove t = 0.

v_r = L/τ = L_t/t

L_t = t L/τ

Ma, ricordando la (1):

L_t = L (t/τ) = Lφ/4π

A noi interessa la distanza da Pappo (d_t) che è uguale a:

d_t = L -  Lφ/4π = L (1 - φ/4π)

Per t = τ /8, ossia per φ = π/2

d_τ/8  = L (1 – π/8π) = 7/8 L

Il primo punto da disegnare (t = τ/8), mettendo Pappo al centro, partendo dalla direzione Pappo-Pippo e andando in verso orario, si ha per φ = π/2 e d = 7/8 L.

Disegniamo, adesso dei punti ancora più interessanti, che ci serviranno anche per la seconda parte.

t = τ/4

φ = 4π t/τ = 4πτ/4τ =  π

d_τ/4 =  L (1 - φ/4π) = L (1 - 1/4) = 3/4 L

t = τ/2

φ = 4π τ /2τ = 2 π

d_τ/2 =  L (1 - φ/4π)  = L (1 - 1/2) = L/2

t = 3/4 τ

φ = 4π t/τ  = (4π 3τ)/(4τ) = 3π

d_3/4τ  = L (1 - φ/4π) = L (1 - 3/4) = L/4

t = τ

φ = 4π t/τ = 4π

d_τ  = L (1 - φ/4π) = L (1 - 1) = 0

E via dicendo… Non è difficile tracciare la curva rossa della parte bassa della Fig. 1

Adesso, però dobbiamo disegnare quello che capita nel piano perpendicolare.

La massima altezza raggiunta sarà legata alla velocità iniziale (in particolare alla componente verticale), ma Peppa, che sa disegnare la parabola della traiettoria della ciliegia (questo l’abbiamo accettato fin dall’inizio), non ha bisogno di fare tanti calcoli. L’altezza massima raggiunta deve rimanere la stessa.

A che angolo corrisponde questa altezza massima? Beh… la parabola raggiunge il suo massimo nel punto di mezzo, ossia quando t = τ/2, che corrisponde a φ = 2π, ossia dopo un giro completo di Pappo. Ciò vuol dire che prima di questo istante la traiettoria deve salire e dopo deve scendere, cambiando di verso.

E’ importante allora vedere cosa capita negli istanti τ/4 e 3τ/4. Essi hanno la stessa altezza, che può essere ricavata direttamente dalla parabola di partenza (azzurra). In quei punti la ciliegia cambia rapidamente direzione. Alla fine (parte alta della Fig. 1) deve arrivare nella bocca di Pappo, come mostrato nello “schizzo” qualitativo di Peppa che è più che sufficiente per lasciare di stucco i suoi fratelli.

Tuttavia (sempre graficamente), Peppa può fare molto meglio e studiare la traiettoria nei dintorni dei punti di cambiamento di direzione e anche della parte finale. Basta che consideri angoli φ abbastanza vicini, i quali ovviamente corrispondono a tempi t e distanze d_t facilmente ricavabili. Dato il tempo è immediato ricavare le altezze dal moto parabolico.

i disegni sono un po' approssimati, ma più che sufficienti a descrivere lo strano moto della ciliegia.

Di seguito un disegno ben più accurato ottenuto da Arturo, in cui il moto della ciliegia si vede da vari punti di vista...

 

Calcoli più accurati possono trovarsi nei commenti del quiz originario.

 

Vi è piaciuto calcolare questo percorso? QUI ne troverete altri!