In attesa di unire domanda e risposta sotto un unico articolo didattico che arricchirà l'archivio nella categoria Fisica Classica, ecco la soluzione del quiz di cinematica rettilinea, di tale semplicità che sia Arturo che Marco hanno solo dato un aiutino, sperando in qualche nuovo temerario. Ho cambiato la parola rincorsa con sorpasso, in modo da permettermi di inserire nella foto di copertina una celebre scenda del meraviglioso fil "Il Sorpasso".

Temerari non ce ne sono stati, ma speriamo che, comunque, anche in piena estate, qualcuno abbia speso un po' di tempo per ragionarci sopra e magari risolverlo.

Diamo per scontate le leggi orarie del moto rettilineo uniforme e di quello uniformemente accelerato, ricavate varie volte sia con o senza i due piccoli integrali che aiutano a ricavarle.

Scriviamole ancora una volta:

x = x₀ + v₀t          .... (1)

è lo spostamento di un certo punto per effetto di una velocità costante v0. Ovviamente, se si considera come origine il punto in cui t = 0 ne x0= 0 si ottiene:

x = v₀ t                  .... (2)

che non è altro che la definizione di velocità costante:

v₀ = x/t

Sia la (1) che la (2) sono anche le equazioni di una retta nel sistema spazio-tempo, dove la (2) è quella che passa per l'origine e v₀ è il coefficiente angolare.

L'equazione oraria più generale del moto uniformemente accelerato è data dalla parabola:

x = x₀ + v₀t + 1/2a₀ t²               .... (3)

dove v₀ è la velocità al tempo t = 0. Come già detto QUI, avremmo nuovamente una relazione lineare tra velocità (non più costante) e il tempo attraverso l'accelerazione costante (a₀):

v = v₀ + a₀t

Se l'oggetto partisse da fermo (v₀ = ₀), si ridurrebbe a:

v = a₀t

che altro non è che la definizione di accelerazione costante:

a₀ = v/t

Tornando alla (3) la possiamo scrivere nel caso particolare in cui il punto (o l'automobile) parte da ferma  (v₀ = 0)nel punto x =o e t=0

x =  1/2a₀t²

che è ancora una parabola avente vertice nell'origine degli assi spazio e tempo.

Fatti questi semplici richiami (per andare più a fondo ricordatevi che il tutto si trova QUI) passiamo al nostro esercizio.

Alla prima domanda non possiamo che rispondere SI. Senza fare troppi calcoli è ovvio che permettendo alla macchina A di continuare ad accelerare, prima o poi deve raggiungere la macchina B che va  a velocità costante.

Affrontiamo, adesso, la seconda e la terza domanda:

L’automobile B viaggia a velocità costante, per cui la sua legge oraria (spazio in funzione del tempo) è data semplicemente da:

x = x₀ + ut

andando a velocità costante poco importa la posizione iniziale della sua corsa e possiamo tranquillamente porre come luogo d’inizio del suo moto la posizione della macchina A ferma, indicandola con x₀ = 0.

x = ut

che nel nostro caso (u = 10 m/s) diventa:

xB = 10 t               (4)

La macchina A parte invece da ferma e si muove di moto uniformemente accelerato

La formula di questo moto è data da

x = x₀ + v₀t + 1/2at²

Nel nostro caso x₀ = 0, così come v₀ = 0, partendo A da ferma.

Per cui la legge oraria si riduce a:

x = 1/2at²

Sostituendo il valore di a = 2 m/s², abbiamo:

xA = 2/2 t2 = t²             …. (5)

Nel momento dell’incontro, che deve avvenire per forza dato che l’automobile A continua ad accelerare, si deve avere xA = xB, perciò

10 t = t²

Ossia:

t(t - 10) = 0

Abbiamo due soluzioni; la prima è ovviamente t = o, dato che le due vetture si incontrano alla partenza di A, per definizione. La seconda, quella che ci interessa, è data da:

t = 10 s    (risposta della terza domanda)

Il percorso effettuato prima dell’incontro, a partire dalla posizione iniziale di A, è quindi:

xA = xB = ut = 10 ∙ 10 m = 100 m  (risposta alla seconda domanda)

 

Un procedimento analogo può essere quello di eliminare t tra la (4) e la (5) e porre, ovviamente xA = xB = x

Si ha dalla (4):

t = x/10

che, inserita nella (5) porta a:

x = x²/100

x (x – 100) = 0

Nuovamente una soluzione si riferisce alla partenza di A (x = 0), mentre la seconda ci dà il valore di x al momento del sorpasso:

x = 100 m   (risposta alla seconda domanda)

Poi basta considerare che dalla (4) si ha:

t = x/10 = 100/10 = 10 s      (risposta alla terza domanda)

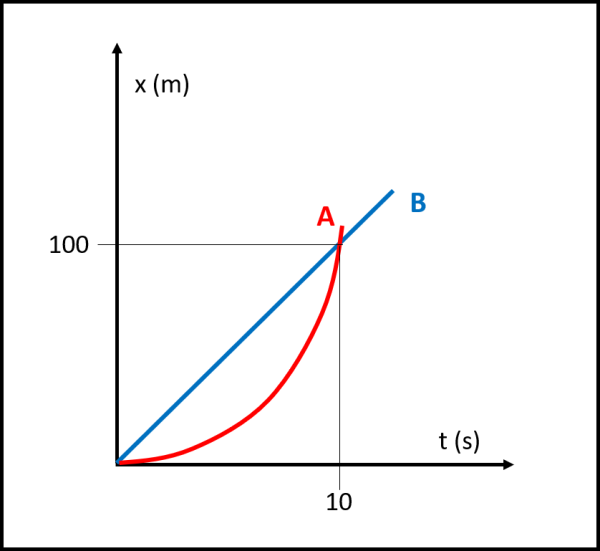
Il tutto può essere visto graficamente. Basta tracciare la legge oraria delle due automobili e leggere le coordinate del secondo punto d’incontro.

Nel moto uniformemente accelerato l’accelerazione è una costante e la velocità varia linearmente con il tempo, per cui si può scrivere :

u = u₀ + at  = at              (l’automobile parte da ferma)

Sappiamo che a = 2 m/s²

E che, nel momento dell’incontro, t vale 10 s

Abbiamo perciò:

u = 20 m/s             (risposta alla quarta domanda).

 

La velocità u può anche essere trovata in quanto non è altro che la derivata della curva dell’accelerazione nel punto voluto.

x = ½ a t²

u = dx/dt = 2a/2 t

per t = 10 s e a = 2 m/s²

si ha:

u = 2 ∙ 10 = 20 m/s          (risposta alla quarta domanda)

Grazie ancora ad Arturo e Marco per il loro aiuto nello stimolare i risolutori nascosti... ci hanno provato, almeno...