Categorie: Fisica classica
Tags: ortogonalità proiettili quiz torre velocità
Scritto da: Vincenzo Zappalà
Commenti:14
Quiz cinematico bidimensionale: Una torre e due spari **
Un quiz, di media difficoltà, che sicuramente vede varie possibilità di soluzione. Io ho usato quella... vettoriale, ma... ormai ho notato la vostra fantasia e interesse, quindi mi aspetto di tutto e di più. Con piacere, noto che nella torrida estate del 2019 (sicuramente la più calda degli ultimi 4800 anni) si stanno facendo vivi lettori prima silenziosi. Forza ragazzi, così mi piacete!
Ormai le difese sono agli sgoccioli e sono rimasti solo due soldati a difendere la città assediata, dall'alto della torre più alta. Hanno un solo colpo in canna e decidono di far fuoco nello stesso momento t = 0 in direzione perfettamente orizzontale. Le due armi da fuoco hanno potenza diversa per cui le velocità di espulsione sono diverse. Uno spara verso destra e uno verso sinistra, in verso perfettamente opposto. Sapendo che ormai dovranno arrendersi, decidono di spendere gli ultimi minuti di libertà risolvendo due piccoli problemi di cinematica (si dice che fossero lettori appassionati dell'Infinito Teatro Medievale del Cosmo):
- Determinare l’istante tP in cui le velocità dei due proiettili sono perpendicolari tra loro
- Determinare la distanza tra i due proiettili al tempo tP
Mi rendo conto che sono problemi relativamente facili per molti dei nostri lettori più esperti, tuttavia, penso che le varie soluzioni proposte -e il richiamo ai concetti base della cinematica e non solo- possano essere d'aiuto e stimolo a molti lettori meno attivi che hanno deciso di passare il tempo estivo impegnandosi in esercizi sicuramente più consoni alle loro capacità mentali. Forza ragazzi, senza paura... la fisica è bella e divertente anche senza parlare di RR, RG e MQ. Quelle sono materie... autunnali e invernali!
14 commenti
Abbiamo a che fare, stavolta, con quello che in Cinematica viene studiato come "moto del proiettile". Esso è caratterizzato dall'avere una componente orizzontale e una verticale. In assenza di attriti, nella direzione orizzontale il moto del proiettile è rettilineo uniforme (non agiscono forze lungo tale direzione) con velocità costante vx. Nella direzione verticale, invece, agisce solo la forza di gravità, diretta ovviamente verso il basso, per cui in tale direzione il moto è uniformemente accelerato. In tale direzione verticale, dunque, la velocità vy varia con il tempo t, in particolare, visto che nel nostro caso il proiettile viene sparato in direzione orizzontale, la componente verticale vy della sua velocità andrà sempre aumentando fino a quando il proiettile, al termine della sua traiettoria parabolica, non tocca il suolo. Estendiamo le considerazioni ai due proiettili. Essi hanno componenti orizzontali delle velocità vxA e vxB, diverse tra loro. La componente verticale delle velocità, invece, è identica per entrambi e pari a gt (verso il basso). Il vettore velocità per ciascuno proiettile considerato all'istante di tempo t, quindi, sarà dato dalla somma vettoriale di vx e vy(t). Quindi, per il proiettile A avremo vxA e vyA(t) , mentre per il proiettile B avremo vxB e vyB(t).
Ipotizzo che il punto di partenza di entrambi i proiettili sia lo stesso, solo che il proiettile A parte verso destra mentre il B parte verso sinistra. Chiamo C il punto comune di partenza. Con coda in C, ora, disegno i due vettori vxA (verso destra) e vxB (verso sinistra) ma aventi entrambi la stessa direzione (orizzontale). Poi, sempre con coda in C, disegno il vettore vyA(t)=vyB(t) (verso il basso) in direzione verticale. A questo punto mi ricavo graficamente la risultante delle due coppie di vettori ora disegnate, cioè quella dei vettori vxA, vyA(t) e quella dei vettori vxB, vyB(t). Sicuramente, a meno di colpi di fortuna, tali due risultanti non risulteranno tra loro perpendicolari. Io cerco proprio la situazione in cui le risultanti sono pependicolari. Beh, allora mi basta considerare il triangolo che ha per vertici il punto C e le punte delle due risultanti prima considerate. Quando questo triangolo fosse rettangolo (come voluto dalla richiesta del problema) , potrei applicare una delle proprietà dei triangoli rettangoli, ossia quella per cui l'altezza relativa all'iptenusa è media proporzionale delle proiezioni dei due cateti. In altre parole potrei scrivere:
cioè (sapendo che le componenti verticali sono identiche e pari a gt, smanettando pochissimo sulla suddetta, arei alla fine:
Questo è l'istante di tempo cercato, in corrispondenza del quale i vettori velocità dei due proiettili risulteranno perpendicolari tra loro.
La distanza tra i proiettili, a questo punto, è presto calcolata:
(per dare dei numeri, occorre conoscere i valori di vxA e vxB. Io direi anche l'altezza della torre, perchè potrebbe succedere che i vettori velocità non ce la facciamo a disporsi perpendicolarmente tra loro prima che i proiettili tocchino il suolo)
ops... ovviamente era
Interessante...
ma mi piacerebbe che entrasse in gioco la velocità iniziale dei due proiettili e non solo la loro componente orizzontale (
). E poi stiamo parlando di vettori e allora... andiamo fino in fondo! (questa è una richiesta più seria).
Ti diverti Arturo, eh!
Comunque, me la fai anche una bella figura da inserire nel testo finale (sempre che sia giusto, ovviamente)...
non so se ho ben capito; i proiettili non vengono più sparati in orizzontale ma in due direzioni qualsiasi?
Ecco 4 figure che chiariscono ciò che avevo descritto nel mio commento.
Nella prima figura ho "fotografato" i due priettili all'istante di tempo generico t dallo sparo:
Nella seconda figura ho semplicemente traslato la costruzione del vettore velocità vA(t) verso sinistra in modo da sovrapporre le due componenti verticali (che sono identiche):
Il triangolo che ha per lati vB(t), vA(t) e il segmento orizzontale in grassetto non è rettangolo.
Ora, nella terza figura, fotografo la situazione dei due proiettili all'istante di tempo cercato tp in cui le due velocità sono perpendicolari tra loro:
Nell'ultima figura, traslo , come prima, la costruzione del vettore vA(t) verso sinistra:
Superfluo dire che ho già l'animazione realizzata con geogebra , implementando per i punti A e B le leggi orarie del loro moto
No, Umberto sparano orizzontalmente come dice il testo...
caro Artù... ma quale è secondo te la velocità di sparo? Ossia, quella iniziale del proiettile... E' solo per fare chiarezza e non rischiare confusioni...
Per aggiungere un concetto ulteriore: sparando come fanno i due soldati il moto parabolico parte dall'altezza massima... ossia dal vertice della parabola.
La velocita' di sparo, orizzontale e, in assenza di attriti, costante nel tempo, e' vxA per il proiettile A e vxB per il proiettile B.
Non so se ci sfugge qualcosa,ma io sono d'accordo con la soluzione di Arturo, anche se ci arrivo con conti diversi. Le componenti orizzontali, che rappresentano la velocità dei proiettili in uscita dal fucile, sono costanti. La componente verticale è invece g*t, ossia dipende dal tempo, pur essendo la stessa per entrambi i proiettili e rappresenta la velocità di caduta istantanea.
Posso pensare di traslare i vettori che rappresentano le due velocità (mantenendoli paralleli a se stessi) in un sistema cartesiano con l'asse y rivolto verso il basso, e l'asse x con l'orientamento naturale, mettendo le code dei vettori nell'origine del sistema; in tal modo le componenti dei vettori diventano le coordinate rispetto a tale sistema. Tanto per usare le stesse notazioni, il vettore A=(-vXA,g*t), mentre il vettore B=(vXB,g*t). Questo posso farlo qualsiasi sia t.
I due vettori sono perpendicolari se e solo se lo sono i vettori traslati; Ricordo adesso la definizione analitica di prodotto scalare, che usa le componenti di un vettore: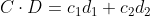
, se C=(c1,c2),D=(d1,d2) sono le componenti di C,D.
ma se due vettori sono perpendicolari il loro prodotto scalare è nullo; pertanto -vXA*vXB+g*tp*g*tp=0
ossia,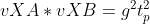
, 
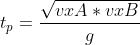
e si arriva allo stesso risultato di Arturo
Solo un abbozzo
Le parabole sono del tipo y=aV^2 t^2 perche x = Vt con V velocità orizzontale di sparo
Le derivate sono
Y'= 2 a V t
I vettori velocita sono tangenti, quindi le derivate sono una inversa dell altra
Cioè 4 a1 a2 v1 v2 t^2 =1
Inoltre per ogni parabola y= 1/2 g t^2 , caduta in asse y
Quindi a1= 1/2 g/V1 e a2= 1/2 g / V2
Sostituendo
t= 1/g radq(V1 V2) , è il tempo richesto
Le x si trovano per sostituzione in x = Vt
Distanza=1/g (v1 +v2) radq(v1 v2)
Come accennavo nella mia soluzione, nel frattempo ho completato una semplice applicazione con geogebra. Nato per giocare" con la geometria, ormai lo uso spesso anche per implementarci situazioni di cinematica. In questo caso, ho implementato le leggi orarie del moto parabolico dei due proiettili, uno verso destra e uno verso sinistra, evidenziando i vettori velocità. Quando tali due vettori risultano tra loro perpendicolari, l'applicazione restituisce sullo schermo il valore di tp. Con tre cursori è inoltre possibile variare il modulo delle due velocità di sparo iniziali vxA e vxB, nonché l'altezza della torre da cui avviene lo sparo.
Ovviamente, per la soluzione rigorosa rinvio a quella pubblicata da Vincenzo. Questo è solo un "gioco" per vedere l'effetto che fa
https://www.geogebra.org/m/wunqwjnz
grazie Arturo! Figura già inserita (il link...) nella soluzione!