L'isola che non c'è *.......* ?
Una strana avventura galattica che racconta di un'epica sfida. Non sempre vince il più forte... L'importante è che Umberto non risponda! Gli asterischi della difficoltà sono a ... piacere.
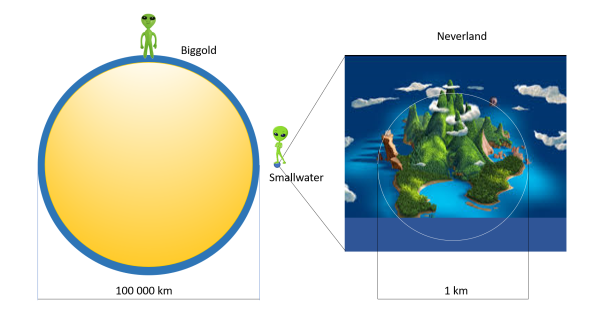
Ai confini della Via Lattea si trova uno dei pianeti più grandi e più strani dell'Universo, completamente ricoperto dall'acqua. Uno strato che, però, non supera mai il chilometro. Sotto l'immenso oceano vi è un nucleo compatto di oro puro a 24 carati. Il suo nome è Biggold ed è abitato da alieni dall'incredibile forza fisica e dalla vita lunghissima, mai minore di 200 anni terrestri. Il suo diametro, acqua compresa, è esattamente 100 000 km.
Idolo di quel mondo ricchissimo e veramente alieno è il più grande nuotatore della galassia, un certo Splashman, detentore del titolo di più veloce circumnavigatore del suo pianeta: 100 giorni terrestri esatti. Il suo stile potente e armonioso gli permette di eseguire manovre quasi impossibili anche in uno spazio ristrettissimo. Oltretutto, ha la capacità di diventare flessibile come un filo d'erba e rigido come una sbarra d'acciaio. Ma la velocità è il suo pregio maggiore.
In un sistema planetario non troppo distante, si trova invece uno dei più piccoli pianeti della Galassia. Il suo diametro è di poche decine di chilometri, ma ha tutti i requisiti dinamici e fisici per essere chiamato pianeta. Lo abitano creature pacifiche e molto intelligenti, che poco gradiscono la superbia e l'arroganza di Splashman. Non solo, però... la popolazione del piccolo corpo celeste, Smallwater, vive in condizioni veramente disastrose, non avendo turismo e nemmeno risorse naturali. Basterebbe anche solo un piccolo pezzo del nucleo d'oro di Biggold per permettergli di venderlo e iniziare una esistenza felice e tranquilla.
Brightbrain, un giovane estremamente astuto del piccolo pianeta disperato, ha però un'idea geniale. Si reca su Biggold e affronta il supercampione proponendogli una sfida. Nel mezzo del piccolo oceano di Smallwater vi è una piccolissima isola, chiamata Neverland, contenuta tranquillamente all'interno di una circonferenza di 1 km di diametro. Bene, se Splashman non riuscirà a fare, nuotando, il periplo perfetto dell'isola in meno di 100 giorni terrestri, Brightbrain e il suo popolo saranno liberi di prelevare tutto l'oro che vorranno dal nucleo di Biggold. In caso contrario saranno per sempre loro schiavi.
Dicono che la risata di Splashman si sia sentita perfino nel lontanissimo terzo pianeta della stella Sole, alla faccia del vuoto cosmico. La sfida è subito accettata, ovviamente, e il supercampione inizia immediatamente la sua nuova, irrisoria, impresa.
Nei mesi che trascorrono dall'inizio della prova di nuoto, i smallwaterani preparano con precisione e tranquillità tutto l'occorrente per gli scavi che iniziano esattamente allo scoccare del centounesimo giorno, come ampiamente previsto dal geniale Brightbrain.
Si dice che di Splashman non si ebbe più notizia per secoli e secoli, forse anche millenni!
Cosa è successo?
La risposta potrebbe essere immediata e lapidaria, ma sarebbe molto meglio cercare di spiegare la magia con una visione più realistica della situazione. Qualsiasi azione "fisica" è ammessa... ma è meglio non andare più indietro degli inizi del secolo scorso.
QUI la soluzione





35 commenti
C'entra di sicuro la gravità visto che è l'unico fattore discriminante capace di deformare il tempo che è la variabile su cui il quiz si basa. Non ho gli strumenti per calcolarla, ma suppongo che i 100 anni terresti su Biggold siano molti ma molti di più su Smallwater per cui Splashman quando nuoterà su Smallwater percepirà il trascorrere del tempo più velocemente, mentre per gli "Smallwateriani" lo vedranno al rallentatore.
Altra cosa possibile soluzione, una struttura fisica di Splashman incompatibile con la gravità di Smallwater. (idea più da biologo). Insomma non ho le competenze per dare una risposta corretta e articolata a dovere, ma sento che l'enorme differenza di gravità dei due pianeti serve a risolvere il quesito. Prendete il mio commento come un suggerimento per chi ha più strumenti di me per approfondire e risolvere.
Colgo l'occasione per ripresentarmi, mi chiamo Marco, sono un biologo ho seguito passivamente e saltuariamente questo blog/circolo/corso di matematica-fisica-astronomia parecchio tempo fa ho lasciato qualche commento qua e là...
Ritorno volentieri e mi impegnerò ad essere più assiduo anche per un altro motivo. A 38 anni suonati e a distanza di 13 anni dalla laurea magistrale in Biologia sto pensando seriamente di iscrivermi a Fisica. Non ho nessuna velleità in ambito lavorativo, i miei prossimi studi saranno la mia personale dichiarazione d'amore verso questo universo che ci ospita e di cui siamo fatti che merita di essere studiato e capito. So bene che non è l'impresa adatta ad una mente della mia età fuori allenamento ma grazie a Dio la mia professione mi consente molto tempo libero da dedicare allo studio e penso che pazienza e tenacia non mi manchino.
Il vostro circolo sarà un prezioso aiuto per allenare un po' la mente ad entrare nel ragionamento matematico di cui i miei studi in Biologia non erano certamente al livello richiesto in facoltà come quella di Fisica. Ringrazio sempre il Prof. Zappalà per la generosità di donare il suo tempo e la sua passione gratuitamente.
Buona giornata a tutti!
caro Spleen81,
ultra benvenuto tra noi in modo assiduo. Un biologo è sempre fondamentale per spiegare tutto ciò che riguarda la vita e la vita è una parte molto importante del Cosmo (forse dovremmo dare un significato più ampio a vita... senza limitarci a quella delle creature come noi e pensare a tutti gli attori dell'Universo come esseri in qualche modo VIVENTI).
Riguardo alla soluzione del quiz... posso dirti che dilatazione di tempi e cose del genere non c'entrano niente. E poi, il nostro nuotatore è veloce, ma non così tanto... E poi tutto è visto nello stesso sistema di riferimento... Chi si avvicina all'orizzonte degli eventi non nota cambiamenti sostanziali. Li nota solo chi sta fuori... E le gravità in gioco sono ben lontane da quelle di buchi neri o stelle di neutroni.
Sotto un certo punto di vista il tutto è molto più semplice... (la biologia, purtroppo c'entra molto poco... a parte certe capacità di Splashman. Tra queste, tanto per tagliare la testa al toro, vi è anche quella di non patire sbalzi di gravità).
Potremmo anche dire che Smallwater ha una densità altissima, tanto da pareggiare la gravità di Biggold...
Insomma, la strada da seguire è tutta un'altra...
a presto e grazie per le belle parole!
Ah... dimenticavo (caro Marco che preferisco a Spleen 81): tra noi del circolo il TU è obbligatorio!
Credo che il trucco sia nel concetto si periplo perfetto.
Il periplo dell'Italia è la navigazione da Trieste a Marsiglia, ed è perfetto se avviene per la via sicura più breve.
Nel nostro caso, Neverland sta dentro una circonferenza che il nuotatore non dovrebbe avere problemi a percorrere nel tempo richiesto, guardandola dall' isola. Se invece la guardo da Biggold probabilmente componendo i moti di rotazione sui propri assi, di rivoluzione intorno alle proprie stelle e poi magari considerando anche i moti relativi delle stelle, la circonferenza non si chiude in tempi inferiori ai 100 gg terrestri, e quindi hai voglia di nuotare, ma nel solito punto non ci torni
chiedo scusa... alla fine avevo scritto Biggold invece di Splashman, ma penso che non abbia influito sulle vostre riflessioni...
Buonasera a tutti.
Magari non c'entrerà nulla ma... una circonferenza di 1 km su un pianeta di diametro 100.000 km è irrilevante, ma su un pianetino di 10, 20 o 30 km di diametro... beh, mi verrebbe da dire che la curvatura sferica si sentirebbe... non è che Il fratello di Aquaman si incastra nelle geodetiche?
direi proprio di no... caro Guido
PICCOLO AIUTO:
Nessuno mi ha ancora chiesto notizie sulle DIMENSIONI dei nostri due eroi...


Effetto Gulliver a Lilliput? Talmente sovradimensionato da non riuscire a nuotare nonostante la sua iperflessibilità?
No, Guido... nuota, nuota... e come nuota!
Buongiorno, premetto che non ho trovato ancora la soluzione al quiz, tuttavia mi sembra che il dato relativo alle dimensioni di Smallwater debba avere significato cruciale, altrimenti non avrebbe senso fornirlo, dato che un'isola delle dimensioni di Neverland potrebbe trovarsi su un pianeta di qualsiasi dimensione che abbia almeno una superficie di 0,5*0,5*3,14 km^2.
direi di no, Guido... poteva anche essere un mondo più grande... poco cambiava...
quello che conta (abbastanza) sono le dimensioni dei personaggi e, per questo motivo, ho preferito far vivere il nuotatore su un mondo molto massiccio... Pensa che fatica per un uomo terrestre vivere su un pianeta come Biggold. Pensa a quanto peserebbe!
Ma il succo del quiz è ben diverso...
Ti ringrazio, comunque, per l'interesse che stai mostrando verso il problema. Domani, aggiungerò un altro piccolo aiuto... oppure do via libera a Umberto!
Mi stupisco un po' che non abbiano ancora parlato Arturo, Leandro, Paolo, Maurizio ...loro hanno via libera...
ah! le vacanze...
Beh mi sono arreso perché ho pensato alla profondita del mare, alla flessibilità ed alla longevità, che non correlavano con le altre informazioni. L unica cosa che mi viene in mente è l effetto Coriolis in un pianeta molto piccolo.
Più che le vacanze, nel mio caso sarà il caldo...
Ho letto e riletto il quiz, i cui dati forniti sono:
diametro Biggold: 100000 km
materiale di cui è fatto il nucleo solido di Biggold: oro (praticamente sulla superficie dell'acqua la gravita di Biggold vale circa 86m/s^2)
spessore strato superficiale d'acqua: 1 km
durata media vita abitanti di Biggold: > 200 anni terrestri
tempo per circumnavigare Bigggold (circa 314159 km) da parte di Splashman: 100 giorni terrestri (praticamente nuota a una velocità di circa 131 km all'ora terrestre)
diametro pianeta Smallwater: poche decine di km (ma è molto denso , tanto da avere in superficie la stessa gravità di Biggold, come leggo nei commenti)
diametro isoletta Neverland: 1 km (quindi periplo pari a 3,14 km)
Ebbene si, sarà il caldo, ma, avendo anche letto gli altri commenti, non riesco a trovare una relazione tra i suddetti dati tale da farmi balenare una possibile soluzione
Allora non sono il solo che non ne esce! Son due giorni che mi lambicco....
Beh in termini di gravità, considerando che la gravità è proporzionale sia al raggio del pianeta che alla sua densità e trattandosi di un pianetino "normale" ( non una stella di neutroni), quindi al massimo è costituito da platino solido , possiamo senz altro affermare che è circa 1/100 di quella terrestre, meno della luna. Rispetto all' enorme gold e' 1/5000 circa.
Anche se non credo influisca sulla soluzione, correggo il valore dell'accelerazione di gravita' sulla superficie di Biggold, data da GM/R^2 (dove M massa la ricavo moltiplicando il volume della sfera per la densita' dell'oro): circa 270m/s^2, avevo dimenticato di moltiplicare per pigreco nel calcolo del volume...
Mah, sono curioso di vedere cosa uscira' dal cilindro del nostro caro Prof questa volta..
Sono stato un po' troppo cattivo... Vi posso dire che tutti dati che ho scritto... NON SERVONO A NIENTE!

La soluzione è ben diversa, anche se la grande massa di Biggold in qualche modo serve ... qualitativamente...
Tornate a quanto detto qualche commento fa...
Splashman è talmente grande che il suo piede copre tutta l'isola e quindi non riesce a nuotare intorno.
Scusate se mi sono intromessa, ma sono affascinata da questo sito.
Buon lavoro.
Paola
grazie Paola!!! e poco importa il quiz... sono stato abbastanza "cattivo", lo ammetto... Fatti sentire
ALTRO AIUTINO-AIUTONE:
ecco una foto ben riuscita di Splashman (presa da molto vicino e anche ingrandita)
e mi voglio rovinare... invitandovi a pensare a un triangolo equilatero...
Stamattina non sono in casa e valuterò le risposte solo nel pomeriggio... SCATENATEVI!!!
Che splashman fosse molto piccolo (o per lo meno con una massa irrisoria, che è ciò a cui pensavo in realtà) l'avevo intuito, ma nonostante ciò non ne ho cavato gran che. Ora questa faccenda del triangolo equilatero m'intriga assai....
Potrebbe essere un triangolo di sierpinski
caro Leandro... sii meno ermetico e spiega meglio cosa sarebbe successo secondo te. Un qualcosa che tende ad avere un'area nulla non mi sembra in sintonia con il nostro problema in cui l'isola c'è e come!
e spiega meglio cosa sarebbe successo secondo te. Un qualcosa che tende ad avere un'area nulla non mi sembra in sintonia con il nostro problema in cui l'isola c'è e come!
Questo triangolo di sierpinski mi riporta alla mente ricordi di dimensioni non intere e il lavoro di Mandelbrot sui frattali e via dicendo...però non capisco bene da dove esce nel ns caso il triangolo, splashman compie una traiettoria circolare sul pianetone e pure una traiettoria circolare deve percorrere sul minuscolo pianetino. Se le dimensioni di splashman rilevano, come Enzo ha suggerito, vuol dire che splashman, presumibilmente approssimabile ad una particella o qualcosa di simile, messo nelle condizioni di dover compiere una traiettoria circolare ma di raggio molto più piccolo, trova insormontabili difficoltà.
Più in là di così non riesco ad andare...peggio di splashman attorno all'isola.
Io non ho detto che l'isola è circolare! Ho solo detto che E' CONTENUTA in un cerchio...
Allora è il vecchio fiocco di neve di Kock, curva frattale di prrimetro infinito a piacere
Seguo con interesse e grazie ai suggerimenti tento un'altra risposta. Se splashman è così piccolo (e non c'era modo di capirlo o di supporlo) allora seguire il contorno delle coste di un'isola molto ma molto frastagliata ci obbliga a considerare un perimetro così irregolare come lunghissimo. Un po' come quando si calcola la superficie del nostro intestino come in svariati metri quadrati grazie ai villi e ai micro villi, ma in questo caso in una sola dimensione. Il tutto dipende dal grado di precisione richiesto per compiere il periplo.
Marco
BRAVI!
Buongiorno professore. Anzitutto grazie per aver fatto pensare a un fiocco di neve in un periodo di caldo torrido... .
.
Però, sommessamente... Splashman non poteva semplicemente circumnavigare l'isola attorno alla circonferenza di un km? Ci avrebbe messo qualche microsecondo... in fondo, lo smallwateriano gli ha chiesto di fare il periplo, non di riprodurre il perfetto perimetro dell'isola (a meno che, matematicamente, periplo non intenda proprio questo... ammetto l'ignoranza...). Ma se il mio ragionamento fila, si dimostra solo una cosa: avere troppo oro in proprietà tende a rendere stupidi...

caro GuidoD io ho scritto:
" il periplo perfetto dell'isola".
in altre parole circumnavigare perfettamente l'isola, ossia seguire bracciata dopo bracciata la sua costa. Io almeno lo intendevo così e penso di non essere stato il solo viste le risposte...
Comunque, l'importante è aver fatto conoscenza con la curva di Koch...
Buongiorno, dopo il cenno al triangolo di sierpinski di Leandro, che mi pare sia stato il primo a tirare fuori i frattali tra gli sventurati che hanno accettato la sfida di Enzo, in effetti la linea di costa infinitamente frastagliata m'è balenata in mente ma il suggerimento al triangolo equilatero me l'ha fatta rigettare perchè l'infame fiocco di neve di Koch me l'ero dimenticato!
Ora faccio questa domanda: ma nel lungo tempo in cui noi ci siamo cimentati col quesito (diciamo 4 giorni), splashman quanta frazione del perimetro dell'isola ha percorso?
caro Guido,
dipende molto dalle dimensioni di Splashman. Diamogli le dimensioni di una formica...o magari di 1mm. Non è difficile calcolare il percorso fermandosi a una certa n che dipende dal lato iniziale (mettiamo 1 km). Provaaaa....