Questo articolo è poco più che uno scherzo e prende spunto da quello splendido romanzo che è Flatland (Flatlandia), scritto nel 1884 da Edwin Abbott Abbott (chi non lo ha letto vada subito a comprarlo!). Un romanzo essenzialmente satirico, che si definisce come “romanzo a più dimensioni”, e che, quindi, la dice lunga sulla sua importanza in un discorso che vuole fare abbracciare strettamente lo spazio con il tempo, ossia riuscire a passare dalle tre alle quattro dimensioni.

A molti di noi sembra ovvio aver capito la rappresentazione grafica dello spazio-tempo, dopo aver accettato di sacrificare una o due dimensioni dello spazio. Tuttavia, il concetto più profondo di questo passaggio è molto più sottile di quanto sembri. Solo comprendendolo bene si può capire la vera differenza tra relatività galileiana e relatività einsteniana. Il tempo, anche se non ce ne accorgiamo, continua a essere considerato come una coordinata “diversa” rispetto a quelle spaziali. La usiamo anche nei grafici della meccanica classica, quando si descrive, ad esempio, la velocità. Però, però, è sempre qualcosa che vive in modo indipendente, capace di modificare lo spazio, ma in qualche modo “intoccabile”. Lui è quello che è e nulla sembra mutarlo.

Invece, per introdurre lo spazio-tempo è necessario fare un passo in più e considerarlo, sotto tutti i punti di vista, una coordinata perfettamente simile alla lunghezza, all’altezza e alla larghezza.  Un’ulteriore informazione che serve per caratterizzare un certo evento. Addirittura può essere espressa nella stessa unità di misura delle altre. Può servire a questo scopo una frase di Einstein che descrive molto bene il problema di fondo che analizzeremo attentamente: “Siccome nella struttura a quattro dimensioni dello spazio-tempo non è più possibile rappresentare obiettivamente l’adesso, sembra naturale pensare alla realtà come a una esistenza quadridimensionale, piuttosto che all’evoluzione nel tempo di una esistenza tridimensionale”.

Pensiamoci sopra e un po’ alla volta il mondo di tutti i giorni ci appare come una errata visione della realtà.  Pur rischiando una trattazione che sembra sconfinare nella “filosofia”, dobbiamo ammettere che il “nostro” tempo è veramente una “strana” grandezza. Diciamo, normalmente, che esso si può dividere in passato, presente e futuro. Tuttavia, il presente, l’unica situazione che fa parte della realtà quotidiana, è quanto di più sfuggente possa esistere. Quanto dura? Un minuto, un secondo, un millisecondo? E’ un po’ come il discorso del limite… dato un certo numero piccolo a piacere possiamo sempre considerare un intervallo di tempo che sia più piccolo di quel numero. In parole povere, il presente, l’unica cosa che ci sembra concreta, è quando di meno reale possa esistere.

Molto più facile è definire il passato e il futuro. Nel primo caso si tratta di tutti gli eventi che non esistono più, ma che sono sicuramente accaduti, nel secondo caso di tutti gli eventi che devono ancora accadere, ma che possono essere legati a quelli passati attraverso le leggi fisiche. La dipendenza di ogni singolo istante con il passato e il  futuro fa sparire qualsiasi concretezza del presente.

E’ molto più logico pensare che la nostra realtà si svolga all’interno di un continuo spaziotemporale quadridimensionale che contiene tutti gli infiniti universi tridimensionali. Ognuno di essi è relativo a un certo istante, ma lo spazio-tempo deve contenerli tutti.

Riflettete bene su questa frase perché già contiene il succo di tutto il discorso.

Matematicamente, anche se appare assurdo per i nostri sensi, ogni avvenimento che a noi sembra svilupparsi nel tempo è già scritto nel continuo spaziotemporale. Non mi picchiate, ma si deve concludere che passato, presente e futuro esistono contemporaneamente. Un diagramma che descrive lo spazio tempo deve quindi essere in grado di riprodurre questa situazione. Solo così si inserisce correttamente la quarta coordinata.

Questa visione va sicuramente contro il concetto di “divenire” che domina ancora il nostro pensiero e quindi è necessario uno sforzo particolare per cambiare la strategia descrittiva. Non per niente, la matematica è perfettamente in grado di descrivere uno spaziotempo realmente quadrimensionale, mentre la filosofia, ossia la scienza del pensiero, non è ancora riuscita a far suo questo cambiamento rivoluzionario.

Non confondiamo, però, la relatività con la meccanica quantistica. La prima non va contro la logica, ma la descrive più correttamente. Essa è quanto di più reale ci sia ed è dominata proprio dalla causalità. La meccanica quantistica, invece, va contro la logica del pensiero e annulla il legame causa-effetto.

Basta, non vogliamo fare filosofia, ma solo mettere i puntini sulle “i”. In poche parole, prima di studiare i passaggi matematici e concettualmente logici introdotti dalla relatività di Einstein e dal metodo grafico di rappresentarla, è bene iniziare a capire esattamente con quale “sistema” abbiamo a che fare. In ogni modo, non preoccupatevi. A mano a mano che andremo avanti, questi concetti saranno ripresi costantemente…

Torniamo al nostro scherzo, che vuole solo mostrarci come sia poco comprensibile (in prima battuta) un passaggio da un mondo  basato su n dimensioni a uno definito da n+1 dimensioni.  Per semplicità descrittiva, seguiamo allora lo schema proposto da Abbott ed eseguiamo il nostro scherzo dimensionale su un abitante del mondo a due dimensioni. Il vantaggio di questa scelta  è indubbio: noi siamo in grado di vederlo dal di fuori, ossia da uno spazio a tre dimensioni, di cui quello a due è solo un caso particolare. Anche questa frase è molto importante: noi cerchiamo sempre di vedere lo spazio dal di fuori, ma in realtà lo vediamo dal di dentro.

Facciamo impazzire un povero cerchio

Noi viviamo in uno spazio a tre dimensioni e lo indichiamo con S3. In questo “mondo” abbiamo un serie infinita di amici che possono aiutarci nello scherzo. Ne abbiamo convinti tre che dopo un po’ di resistenza (sono sempre figure geometriche…) hanno accettato. Non li presento ancora per creare un po’ di “suspence”, ma penso che li riconosciate velocemente.

Chi subisce lo scherzo è un cerchio, di nome CE,  di grande intelligenza (anche se un po’ superbo), che vive nello spazio S2, a due dimensioni. In quello strano spazio, non è facile intuire facilmente con chi si ha a che fare. Un rettangolo e un segmento si vedono nello stesso modo, ma anche una circonferenza, e molte altre figure (pensateci bene). Tutte appaiono come dei segmenti! Bisogna toccare, valutare attentamente lo spessore delle linee e applicare tanti altri piccoli accorgimenti per identificare i vari abitanti. Inoltre, nello spazio di CE, la differenza tra bambini e adulti sta solo nelle loro dimensioni (questa è una mia aggiunta…).

Il nostro amico  CE sa di essere particolarmente dotato e… se la tira un po’. E’ il personaggio giusto per subire uno scherzo un po’ “cattivo”, ma anche per imparare  qualcosa che per lui è veramente incredibile. Per noi, invece, tutto è più semplice, dato che possiamo spostarci nella terza dimensione (che lui non può vedere) e assistere alla sua disperazione crescente. Immaginiamo di posizionarci a una certa altezza (parola sconosciuta a  CE) e disegnare cosa succede nello spazio piano S2.

In Fig. 1 ci sono diversi momenti dello scherzo “visti dall’alto”. Ciò che si vede è, quindi, lo spazio di CE a due dimensioni.

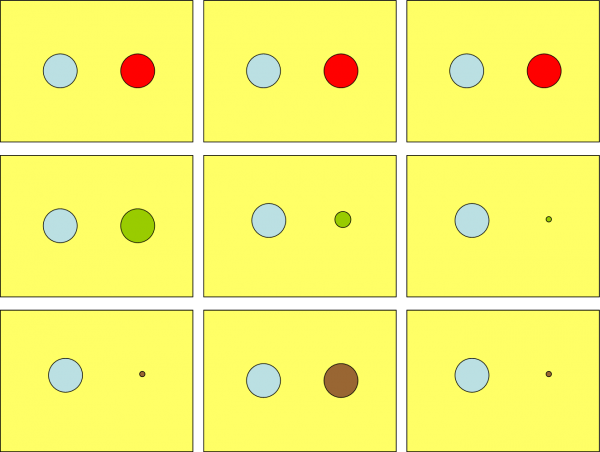
Cominciamo con la prima riga. A sinistra CE vede improvvisamente comparirgli davanti CI. Un attimo di sorpresa, ma subito dopo inizia il colloquio. CI chiede a CE: “Chi sono?” CE non ha problemi a dirlo: “Sei un cerchio come me, di colore rosso; ti riconosco da tante piccole sfumature e so che non puoi essere altro che un cerchio”. CI si mette a ridere e poi dice a CE che adesso si muoverà rispetto a prima ma resterà sempre lì davanti a lui.

Un attimo dopo ecco la seconda scena. CE non ha problemi a dire: “Sei rimasto tale e quale a prima. E’ ovvio…”. CI risponde: “Nemmeno per sogno. Ti posso assicurare che mi sono mosso e anche di molto! Ti voglio aiutare e mi muovo di nuovo, ma cerca di guardare meglio…”. La situazione è quella della terza scena della prima riga. Ancora una volta niente sembra cambiato, ma CI scoppia in una risata sguaiata: “Niente da fare, non riesci a vedere nessuna differenza. Sei proprio un incapace. E tutti dicono che sei intelligente…”.

CE rimane solo e non sa che pensare: “Quello strano cerchio è sicuramente fuori di testa. Restava fermo e mi voleva convincere che si muoveva.  La voce era la sua e anche l’aspetto. Mah… ce ne sono di tipi strani…”.

Poco dopo si passa alla situazione descritta nella seconda riga. Accidenti… eccolo di nuovo! Ma no, non è lui, dato che è di colore verde. CE prende l’iniziativa: “Non dirmi chi sei. Ti vedo benissimo sei un cerchio come me.” Il nuovo personaggio risponde subito: “Ciao, mi chiamo CO e sono amico di CI…  Voglio una conferma della tua incapacità nel riconoscere le persone. Stai attento, perché adesso mi muoverò”. Nella seconda immagine si vede un cerchietto verde un po’ più piccolo di prima. Ma la voce è la stessa e anche la sfumatura del colore. “E allora” dice “chi sono?”. CE è un po’ interdetto. Non può dire che CO è rimasto uguale a prima. E’ sempre un cerchio, ma di dimensioni minori, proprio come se fosse diventato più giovane. D’altra parte, colore e voce non possono ingannarlo: è sempre la stessa persona… solo che è ringiovanita! Impossibile…

CE è ancora lì con la bocca aperta ed ecco che CO cambia ancora. Adesso non è altro che un cerchietto talmente piccolo che sembra un punto, un vero neonato. Eppure è sempre lui e sa parlare già molto bene, quando gli chiede: “Sai dirmi, finalmente, chi sono?”. CE non sa che dire e non riesce a spiaccicare una parola che sia una. E’ del tutto allibito: mai aveva visto un cerchio ringiovanire!

Non si è ancora ripreso dallo stordimento ed ecco che davanti a lui si presenta un nuovo cerchio dal nome di SFE. “Basta, caro CE, questo è l’ultimo tentativo. Sono una cara amica di CI e di CO. Se non sai dirmi chi sono vuol dire che non vali niente!”. Nel mondo di CE nessuno può cambiare il colore e la voce: è costretto ad ammettere che chi è davanti a lui è un personaggio ancora diverso. L’aspetto, però, è lo stesso con cui l’aveva lasciato CO. Davanti a CE c’è un piccolo cerchietto, molto giovane, che sa parlare molto bene ed è di colore marrone.

Un attimo dopo, SFE diventa improvvisamente come gli erano apparsi sia CI (per tutto il tempo dell’incontro) sia CO (al momento iniziale). CE suda abbondantemente (sudano anche nello spazio S2…) e si mette quasi a urlare: “Tu sei un cerchio, solo e soltanto un cerchio come me, ma come accidenti hai fatto a invecchiare così velocemente!? Un attimo fa eri un neonato e adesso sei un adulto tale e quale a me. Che stregoneria è mai questa?”. SFE sembra divertirsi moltissimo e gli risponde: “Questo è niente. Io posso variare la mia età come voglio, anche muovendomi sempre in avanti”.

Accidenti… CE si sente svenire e teme di diventare una parabola, l’aspetto di tutti i cerchi poco prima di morire. Davanti a lui SFE è tornata a essere una neonata, un punto, o poco più, di color marrone. Questo è veramente troppo anche per lui e sicuramente, se ne uscirà vivo, non se la tirerà più. Ci sono persone sicuramente più intelligenti di lui!

CO, CI e SFE decidono che lo scherzo è finito e ricompaiono tutti e tre assieme nelle forme del cerchio simile a CE. Poi iniziano a spiegare…

Non voglio certo scrivere un altro romanzo, scopiazzando da Flatlandia, e quindi posso svelare il semplice trucco. CO, CI e SFE non sono altro che un cono, un cilindro e una sfera, abitanti dello spazio S3 (Figura 2). Loro non hanno fatto altro che muoversi dall'alto verso il basso nella “loro” dimensione z (del tutto invisibile a CE) e fermarsi di tanto in tanto. La sezione con il piano-spazio S2 ha fatto vedere a CE  figure sempre uguali, ma di dimensioni diverse. Qualcosa che CE credeva di conoscere, ma che invece non conosceva affatto: a volte -ha imparato- l’apparenza inganna.

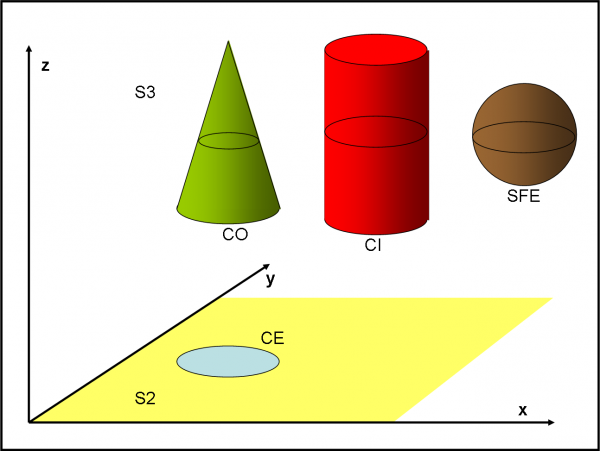
Giura che non sarà più superbo o arrogante e chiede ai nuovi tre “strani” amici di spiegare esattamente cosa o chi sono. Loro lo fanno e CE, che intelligente lo è per davvero, capisce tutto anche se sa che non potrà mai disegnare esattamente il mondo S3. Sa, però, come fare a rappresentare una sfera, un cono  e un cilindro nel suo spazio S2: qualcosa uguale a un cerchio che può ingrandire o restringersi o anche rimanere sempre uguale a se stesso. Impara anche il modo di legare la nuova coordinata che non può disegnare alle due che invece conosce. Basta usare un po’ di matematica e scrivere delle formule di trasformazione o qualcosa del genere. A questo punto, anche CE potrebbe vivere in S3, anche se solo con le sue due dimensioni. Resterebbe sempre lo stesso, ma potrebbe spostarsi lungo la nuova coordinata z.

Bene, tante parole per dire che cosa? Ben poco di più (però… mi sono divertito a raccontare lo scherzo!). Il concetto è semplice: per aggiungere veramente una nuova dimensione a S2 bisogna trovare un modo rigoroso che la sappia legare alle altre due. In qualche modo mettere la terza coordinata sullo stesso livello delle compagne.

Quello che dobbiamo fare noi, allora, è solo e soltanto cercare di legare il tempo allo spazio, considerandolo, però, come una "normale" coordinata in più.

Il tempo quindi deve essere qualcosa che esiste in tutta la sua totalità nel nuovo spazio (lo spazio-tempo) e che può assumere valori negativi e positivi e anche zero, tale e quale alle ben conosciute x,y,e z. Niente di più e niente di meno.

Faccio un esempio per far comprendere meglio il concetto finale. Nello spazio S2 posso scrivere una grandezza, ad esempio la distanza, utilizzando una combinazione di x e y. Lo stesso posso fare nello spazio a tre dimensioni con una combinazione di x, y e z. Non resta che poter scrivere una distanza (o quello che sarà) anche nello spazio a quattro dimensioni, dove ovviamente le quattro dimensioni sono x, y, z e t. Il punto nello spazio S2 è definito da una x e una y. Nello spazio S3 da una x, una y e una z. Nello spazio S4 (lo spazio-tempo) il punto prende il nome di evento ed è caratterizzato da una x, una y, una z e una … t. Niente di così difficile, direi… Avendo due punti si può sempre scrivere la loro distanza. Lo stesso dobbiamo riuscire a fare nello spazio-tempo scrivendo la "distanza" di due eventi.

Capito il concetto, non vi è poi nessun problema a eliminare una o anche due delle coordinate per semplificare i disegni. Ovviamente… non il tempo!

Il tempo è una coordinata speciale?

Il concetto che ho cercato di spiegare è tutt’altro che banale. Credetemi. Qualcuno potrebbe pensare: “Sappiamo già come collegare il tempo con le altre coordinate. Lo facciamo tutte le volte che descriviamo il moto di un oggetto.” Dobbiamo, però, fare sempre molta attenzione. Ad esempio, i due diagrammi riportati nella Fig. 3 sembrano uguali ma rappresentano concetti profondamente diversi. La distanza tra P e Q nella parte di sinistra è una distanza spaziale, calcolabile facilmente nello spazio euclideo x,y. P e Q sono due posizioni dell’oggetto che descrive la traiettoria. Il secondo, a destra, mostra, invece, come varia lo spazio (tre dimensioni compresse in una sola) in funzione del tempo. I due punti P e Q rappresentano, adesso, due eventi dell' oggetto. La "distanza" PQ è un intervallo tra due eventi. La differenza esiste e come!

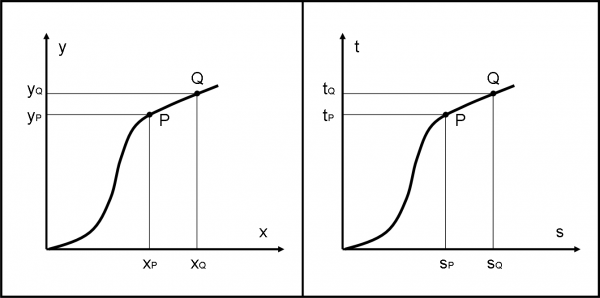
In poche parole, la prima è una traiettoria spaziale, la seconda è la famosa linea di Universo… Nella prima non sappiamo come viene percorsa la traiettoria. Nella seconda sì: conosciamo tutto di lei.

Non fatevi confondere dal fatto che vi è solo una s e non uno spazio a tre dimensioni. Basterebbe disegnare uno spazio a tre dimensioni e aggiungere la quarta (se ne fossimo capaci). Tuttavia, una, due o tre coordinate spaziali fanno poca differenza, concettualmente, e quindi adattiamoci a vedere lo spazio molto "ristretto". L'importante è avere inserito il tempo e disegnare un diagramma spazio-temporale. Ci torneremo a tempo debito, ovviamente. Ricordate, però, che l'ultimo tipo di diagramma l’abbiamo usato molto spesso sia per disegnare il cono di luce che  le figure degli ultimi capitoli della QED. D'ora in poi dovremo sempre usare questa rappresentazione, se vogliamo che il tempo entri  in gioco ad armi pari.

La differenza concettuale è già evidente nello spazio-tempo euclideo (quello di Galileo e Newton). Lo sarà molto di più nello spazio-tempo della relatività enisteniana. Il concetto va capito adesso, prima di complicare le cose con trasformazioni più intricate e meno intuitive. Anzi, la prossima volta, disegneremo lo spazio-tempo galileiano, tanto per capirne l'essenza. Poi lo lasceremo da parte, per confrontarlo, alla fine, con quello relativistico. Vedremo che in esso il tempo rimane qualcosa di scollegato dal resto. Solo la relatività ristretta  riuscirà a fare veramente ciò che è capitato al nostro amico CE.

Scusate se questo articolo è stato lungo e -forse- più filosofico che matematico. L’ho voluto inserire solo per fare comprendere, prima di partire in… quarta (dimensione?), come non sia  immediato, concettualmente, aggiungere una coordinata  a un certo spazio a n dimensioni. Inoltre, come le cose si complichino ancora di più se la nuova dimensione è proprio il tempo.  D’ora in poi procederemo con molta più lentezza, cercando di spiegare, passaggio  per passaggio, come si riescono a ottenere i principi base della relatività speciale e la sua rappresentazione grafica. I vari capitoli saranno anche decisamente più CORTI!

Il tempo è una brutta bestia e solo Einstein poteva trattarlo con tanta disinvoltura, aiutato dal quel genio della geometria che era Minkowski.