Categorie: Relatività Spazio-Tempo
Tags: paradosso dei gemelli relatività ristretta
Scritto da: Vincenzo Zappalà
Commenti:12
Come distruggere “osservativamente” il paradosso dei gemelli ***
Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento
Innanzitutto, vediamo come sia semplicissimo calcolare graficamente quanto passi più lentamente il tempo per chi viaggi a grande velocità su un’astronave, se misurato da un osservatore fermo. Sfruttiamo il fattore di Lorentz, proprio quello che ci permette di valutare la dilatazione del tempo in funzione della velocità dei una astronave.
Eliminiamo, innanzitutto, un errore che si commette spesso. Si legge e si sente dire che il tempo per chi viaggia su un sistema in rapido movimento passa più lentamente. Questa affermazione è sbagliata concettualmente. E’ giusto dire che il tempo dell'astronauta passa più lentamente per chi osserva il viaggiatore da un sistema esterno in quiete, ossia che rimane fermo. Ci torneremo sicuramente sopra varie volte, ma è bene eliminare subito questo concetto veramente deleterio. Un’astronave che si avvicina sempre più a un buco nero, ossia acquista una velocità sempre più prossima a quella della luce, appare fermarsi sull’orizzonte degli eventi a un osservatore esterno. Per il viaggiatore, il tempo passa normalmente ed egli attraversa l’orizzonte senza alcun problema. Questo fatto ci porta al tempo proprio che sarà fondamentale nella relatività speciale.
L’orologio di chi viaggia e quello di chi sta fermo girano nello stesso modo, ma è quello dell’astronave che rallenta se visto dall’osservatore esterno. E', nuovamente, solo e soltanto un problema di sistema di riferimento
Poniamo per semplicità X = v/c, ossia X sia il rapporto tra la velocità dell’astronave e quella della luce. In altre parole, esso ci dice a quale frazione della velocità della luce sta viaggiando la nave spaziale. X = 0.1 vuol dire che va a un decimo di c, 0.9 che va a 9/10, e via dicendo. Ovviamente, se v = 0, X = 0 (astronave ferma) non vi è dilatazione del tempo. Se, invece, v = c, X = 1 la dilatazione è massima e l’orologio dell’astronave appare fermarsi. La formula che lega il tempo T’ di chi sta fermo con quello T di chi si muove è data da:
T = T’ (1 - X2)½ … (1)
Per adesso, prendiamola per buona, ma la ricaveremo in modo molto semplice...
Poniamo, inoltre, Y = T/T’. Y indica, così, il rapporto tra il tempo di chi viaggia e quello di chi sta fermo. In altre parole, di quanto rallenta l’orologio di bordo rispetto a quello di chi sta a terra. Ovviamente, come già detto, Y = 0 se X =1. Il che vuol dire che andando alla velocità della luce l’orologio di bordo non gira più. Ciò vorrebbe dire che per un fotone (se potesse avere un orologio) il tempo non passerebbe, se visto da terra… Tuttavia lui viaggia e come e quindi ci raggiunge sicuramente.
La formula (1) diventa:
Y = (1 – X2)½ e ancora (con passaggi elementari):
X2 + Y2 = 1 … (2).
Accidenti! La (2) non è altro che l’equazione di una circonferenza che ha il centro nell’origine degli assi X e Y. Con questo cerchio possiamo fare molte cose. Notate che ormai il tempo è diventato coordinata a tutti gli effetti...
La Fig. 1 (a sinistra) ci illustra questa semplice, ma utilissima rappresentazione.
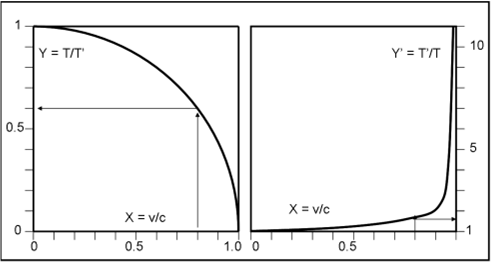
Scegliendo la velocità di crociera si può subito sapere di quanto si dilaterà il tempo dell’astronauta, ossia di quanto il suo orologio girerà più piano di quello terrestre. Ad esempio, se decidiamo che viaggi all’80% della velocità della luce, l’orologio dell’astronave rallenterà del 60%. In altre parole segnerà l’anno 6 quando il nostro segnerà l’anno 10 (sempre che si sia partiti entrambi da zero).
La Fig. 1 (a destra) illustra il viceversa. Ossia rappresenta Y’ = 1/Y in funzione sempre del rapporto X. Y’ è ovviamente il rapporto tra il tempo nostro e quello dell’astronave. Rispetto a quest’ultimo, il nostro orologio viaggia sempre più velocemente a mano a mano che si avvicina alla velocità della luce. Quando la raggiunge, il nostro tempo (T’) è infinito, l’orologio gira in modo pazzesco! Un fotone vede scorrere tutto l’Universo in un attimo. Se invece la velocità dell’astronave diventa zero il nostro tempo e quello dell’astronave diventano nuovamente uguali (Y’ = 1).
La perfetta simmetria
Quanto detto dimostra ancora una volta che le conclusioni sono relative al sistema di riferimento scelto. Se consideriamo il nostro tempo come riferimento, quello dell’astronauta viaggia più lentamente andando verso lo zero. Se consideriamo come riferimento il suo, è il nostro che viaggia in modo sempre più rapido tendendo a infinito.
In entrambi i casi, però, stiamo considerando noi fermi e l’astronauta in viaggio. Lui, però, cosa vede? Esattamente la stessa cosa, ribaltata. Per lui, che può giustamente considerarsi fermo, siamo noi che andiamo a velocità più o meno alta e che subiamo una dilatazione del tempo. La sua astronave è ferma ed è la Terra che si muove a velocità altissima. Ne consegue che nel suo sistema di riferimento è il nostro orologio che appare girare più lentamente, ecc., ecc.
In parole semplici: i due sistemi di riferimento sono inerziali e quindi è possibile invertire completamente i risultati. Un’astronave che viaggia rispetto a una Terra ferma porta alle stesse conclusioni di un’astronave ferma che vede la Terra viaggiare a grande velocità. Ne consegue che per chi sta a terra sarà l’astronauta a invecchiare di meno (è lui che si muove). Per l’astronauta è invece chi sta sulla terra a restare giovane (è la Terra che si muove).
Siamo arrivati nuovamente al paradosso dei gemelli. La relatività ristretta, che si occupa solo di sistemi inerziali, ossia che si muovono uno rispetto all’altro con velocità rettilinea uniforme, comporta questa assurdità: entrambi i personaggi devono invecchiare di meno, dato che entrambi applicano correttamente le formule della dilatazione del tempo.
Il paradosso dei gemelli è ancora oggi spunto per dibattiti più o meno sensati e più o meno complicati. Tuttavia, come tutti i paradossi, non è difficile risolverlo. Basta scegliere le giuste condizioni per affrontarlo. Quello dei gemelli si scioglie come neve al Sole se passiamo alla relatività generale, ossia se si considerano sistemi NON inerziali, sistemi di riferimento che si muovano uno rispetto all’altro con velocità non uniforme, ossia sistemi accelerati.
Ecco che diventa fondamentale conoscere le basi della meccanica classica. Anche lei dice che se si passa da un sistema inerziale a uno accelerato le regole cambiano e uno stesso fenomeno deve essere descritto in modo diverso. Nascono addirittura delle forze fittizie, come quella centrifuga o quella di Coriolis. Ed ecco anche perché, per parlare di Universo, di tempo relativo, di spazio-tempo, ecc., ecc., è necessario conoscere la fisica elementare. Senza di lei il salto verso la relatività diventa un’impresa senza speranza.
Innanzitutto, ribadiamo ancora una volta che il paradosso dei gemelli perde di significato quando il moto dell’astronave e quello della Terra vengono considerati nell’ambito della relatività generale. La Terra può essere considerata un sistema inerziale, ma non certo l’astronave, la quale, per raggiungere una certa velocità deve accelerare e, per tornare a casa, decelerare. Il che implica un moto accelerato e quindi un sistema non inerziale. La simmetria si è rotta. Ne consegue che solo l’astronauta subisce una variazione del proprio tempo e ne conserva il segno al suo ritorno sulla Terra. E’ veramente invecchiato di meno, perché solo lui ha subito accelerazioni e decelerazioni.
Nel libro “L’Infinito Teatro del cosmo” avevo presentato un metodo relativamente semplice per risolvere il paradosso anche ragionando solo nell’ambito della relatività ristretta. Si analizzava il sistema di riferimento dell’astronave che, pur mantenendosi inerziale, cambiava direzione dopo aver raggiunto la stella. Ne conseguiva un “salto” temporale che permetteva di confrontare gli anni effettivi dei gemelli e dare ragione a chi stava sulla terra e pensava di invecchiare di più.
L’osservazione diretta non tradisce mai
Giocherellando, però, con le figure che vi ho mostrato prima, mi è venuto spontaneo considerare anche un altro modo per risolvere il paradosso: un modo puramente “empirico”, ossia osservativo.
Si può dimostrare che chi viaggia è veramente invecchiato di meno, pur mantenendo immutata la simmetria apparente tra chi viaggia e chi sta fermo, come impone la relatività ristretta.
Attenzione, però: non si risolve veramente il paradosso, ma, seguendo cosa succede, si arriva a una conclusione univoca. In altre parole, ci si disinteressa del problema “teorico” o concettuale sulla perfetta inversione dei sistemi di riferimento dettata dalla relatività ristretta, ma si valuto solo ciò che capita osservativamente.
Ciò che mi piace in questo approccio è il fatto che si deve partire dal caro e amato cono di luce.
Solo un accenno, ma quanto basta per capire tutte le connessioni che esistono tra le grandezze in gioco. Attraverso di lui si può fare di tutto e di più… e Minkowski ce lo insegnerà.
Disegniamo, allora, in Fig. 2, il cono di luce della Terra come “sfondo”. Lo mettiamo orizzontale. Lo spazio, ossia la distanza tra la Terra e tutto il “resto” sia l’asse delle ordinate. Le distanze su di esso si misurano in anni luce. L’asse delle ascisse è invece il tempo terrestre, espresso in anni. Sia T’ questo tempo. La linea di Universo della Terra è, ovviamente, proprio l’asse del tempo.
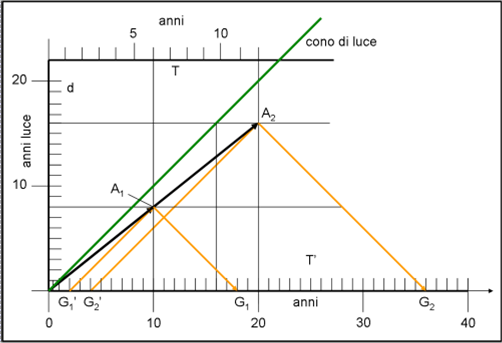
Il bordo superiore del cono di luce futuro, al tempo T’ = 0, è la linea verde, inclinata di 45°. L’inclinazione ottenuta dipende dal fatto che l’unità delle ascisse è l’anno e quello delle ordinate l’anno luce: in un anno di tempo, la luce percorre proprio una distanza di un anno luce. Ricordiamo che, per definizione stessa di velocità della luce, niente, originatosi sulla Terra, può superare la linea verde. Teniamo bene a mente che stiamo vedendo tutto nel sistema di riferimento della Terra intesa come immobile.
Facciamo partire l’astronave A (linea nera), al tempo T = T’ = 0, a un velocità che sia pari all’80% di quella della luce. La Fig. 2 illustra l’astronave inviata nello spazio per sempre (non è previsto il ritorno). Dopo 10 anni terrestri l’astronave giunge sulla stella A1 che dista 8 anni luce da noi. Questo è un dato di fatto, dato che la sua velocità è stata proprio scelta così: v = 0.8c (circa 240 000 km/sec). L’astronauta guarda il suo orologio. Sembra tutto normale, ma sa che rispetto a quello terrestre esso è andato più piano e gli è facile calcolare di quanto attraverso la Fig. 1 che si è portato dietro: essa ci dice che vale T = 0.6 T’, ossia T = 0.6 · 10 = 6 anni. Il suo orologio nel sistema di riferimento terrestre segna 6. Ma, a noi, per adesso, interessa poco quello che vede il viaggiatore…
Possediamo ormai telescopi fantastici e vogliamo vedere direttamente il suo orologio. Quando, però potremo vederlo? Beh… si deve, comunque, aspettare che la sua luce arrivi fino a noi. Per ottenere questo bisogna aspettare 8 anni (la stella dista 8 anni luce da noi). L’orologio dell’astronave, che segna l’anno 6, viene visto sulla Terra in G1, nell’anno 10 + 8 = 18. Dalla pura osservazione possiamo dire che quando l’orologio dell’astronauta segna 6 noi siamo già a 18. Il suo orologio è andato tre volte più lento del nostro.
Anche l’astronave è munita di un fantastico telescopio. Cosa osserva l’astronauta quando giunge in A1? Vede la luce che giunge dalla Terra partita nell’anno 2 da G1’. In altre parole, l’orologio terrestre segna 2 mentre il suo (secondo la Fig. 1) segna 6. Per l’astronauta l’orologio sulla Terra è andato tre volte più piano del suo. Fino a qui nessun problema: cambiando sistema di riferimento si è invertita la visione degli eventi. La simmetria è perfetta e la relatività ristretta è soddisfatta. Ricordatevi che stiamo eseguendo osservazioni perfettamente realistiche. Nessuno può dire che quanto descritto non sia giusto.
L’astronauta riparte (anzi, non si è mai fermato se no avrebbe variato velocità) e giunge dopo altri 10 anni terrestri sulla stella A2 che dista da noi 16 anni luce. Per raggiungerla ha, ovviamente impiegato, totalmente, 20 anni terrestri. Tuttavia, cosa segna il suo orologio ? Beh… facile a dirsi, visto che la velocità è sempre la stessa e che la distanza percorsa da A1 a A2 è nuovamente 8 anni luce. La dilatazione del tempo non cambia e quindi l’orologio segna 6 anni in più di prima, ossia 12.
Notate che sulla parte alta della figura ho inserito la scala del tempo dell’astronauta (il suo orologio visto nel sistema di riferimento terrestre), ottenuta proprio moltiplicando il tempo terrestre per il fattore 0.6. Posso inserire questa scala nel sistema di coordinate terrestri. Se cambiassi sistema di riferimento questa scala non sarebbe più valida, ovviamente. Inoltre, questa scala di tempo vale solo per la velocità scelta. Se cambio velocità, cambia il fattore di Lorentz e quindi anche la scala. Nell’esempio che stiamo descrivendo, però, questa scala è del tutto valida per guardare l’ora del viaggiatore spaziale nel nostro sistema di riferimento.
In A2, quindi, l’orologio dell’astronauta segna 12. Quando viene visto sulla Terra questo orologio con questa ora? Ovviamente, in G2, nell’anno 36 (18 + 18). Cosa si dice sulla Terra? Che il tempo dell’astronauta ha continuato ad andare tre volte più lento del nostro. Tutto secondo le regole. E l’astronauta giunto in A2? Il suo orologio segna 12 (esso segna il tempo che si vedrebbe dalla Terra), mentre quello che vede sulla terra soltanto 4 (luce partita da G2’). Anche per l’astronauta le cose non cambiano. Sulla terra il tempo continua a viaggiare tre volte più lentamente del suo. La simmetria si mantiene perfetta, in accordo con la relatività ristretta.
Potremmo andare avanti all’infinito, ma le cose non cambierebbero. La nostra simulazione è perfettamente logica, esatta e si basa sulle pure osservazioni. Non solo, ma vi è completa simmetria tra chi viaggia e pensa di stare fermo e chi sta fermo ma viene visto viaggiare. Per sapere chi è veramente invecchiato di più bisognerebbe confrontare gli orologi a uno stesso istante in uno qualsiasi dei due sistemi di riferimento. Questo non potremmo mai farlo, dato che noi e l’astronauta ci allontaniamo sempre di più.
Tuttavia, possiamo provarci, cambiando la simulazione. Questa volta, infatti, quando l’astronauta arriva in A1 non prosegue verso A2, ma torna verso la Terra. Finalmente, sarà veramente possibile confrontare gli orologi nello stesso luogo. Manteniamo, ovviamente, sempre uguale la velocità dell’astronave (se no addio alla relatività ristretta) e teniamo conto del cambiamento di direzione valutando SOLO le osservazioni.
Consideriamo la Fig.3. Fino ad A1 tutto funziona come prima, con entrambi i protagonisti (noi e l’astronauta) che osservano l’orologio dell’altro andare tre volte più piano. Noi sulla Terra, siamo già nell’anno 18, in quanto abbiamo osservato l’orologio dell’astronauta quando era in A1 e segnava 6. Sappiamo, però, anche molto bene che il viaggio di andata e ritorno deve durare 20 anni. Questo è un dato di fatto, dato che la velocità dell’astronave è sempre la stessa e percorre 8 + 8 = 16 anni luce in 20 anni: 10 per arrivare in A1 e 10 per tornare sulla Terra. Nell’anno 20 la nave spaziale DEVE tornare.
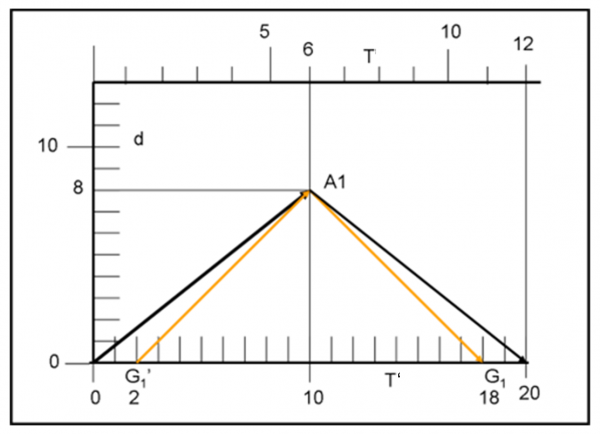
E infatti è così. Nel 20 la nave atterra. Cosa concludiamo noi sulla Terra? Che il viaggio di ritorno è stato rapidissimo: solo 2 anni. Nel 18 l’orologio era ancora in A1 e adesso eccolo davanti a noi! Nel 18 segnava 6 e adesso segna 12. DEVE sicuramente segnare 12 dato che nel viaggio di ritorno l’orologio dell’astronauta ha continuato a rallentare secondo il fattore di Lorentz.
Noi quindi vediamo il nostro che segna 20 e il suo che segna 12. Cosa vede l’astronauta appena giunto sulla Terra? Ovviamente la stessa cosa: il suo orologio segna 12 e quello della Terra segna 20. Accidenti! Ma, allora, il tempo è veramente passato più lentamente per l’astronauta. E’ lui che è invecchiato meno. Dov’è finito il paradosso? Non esiste più…
Un attimo, un attimo. Per cantare vittoria, dobbiamo ancora vedere se si è mantenuta la perfetta simmetria tra chi sta sull’astronave e chi sta sulla Terra. Dunque, per noi sulla Terra sono passati 2 anni (20 – 18), mentre l’orologio dell’astronauta ne segna ben 6 in più (12 – 6). Per l’esattezza, l’orologio spaziale ha viaggiato tre volte più veloce di quello terrestre.
Cosa dice, invece, l’astronauta? Il suo segna 6 anni in più di quando era in A1 (e quindi 12). Quello della Terra, invece, segna ben 18 anni di più (è infatti l’anno 20) di quando l’aveva osservato da A1 (20 – 2). Per lui l’orologio della Terra è andato tre volte più veloce del suo.
La simmetria è rispettata perfettamente anche nel viaggio di ritorno.
Da un punto di vista puramente osservativo, che è poi proprio la realtà, il viaggiatore è veramente il più giovane. Per lui sono passati 12 anni (il suo orologio segna 12), mentre per chi sta sulla Terra ne sono passati 20 (il nostro orologio segna 20).
Dov’è finito il paradosso? Praticamente non esiste più. E’ uno e uno soltanto colui che è invecchiato di meno. Proprio quello che ci direbbe la relatività generale.
E’ chiaro che abbiamo dimostrato la verità nascondendo il vero paradosso sotto il tappeto. Tuttavia, la dimostrazione è a prova di bomba. Come si spiega? Facile, in fondo. Nell’andata abbiamo considerato la nave allontanarsi da noi, al ritorno invece avvicinarsi. In un modo o nell’altro abbiamo rotto la costanza del moto rettilineo uniforme dell’astronave, senza toccare il nostro. E’ quindi ovvio che il paradosso sparisca automaticamente. Il paradosso (da un punta di vista concettuale) continua a esistere nella relatività ristretta, ma le “osservazioni” ci dimostrano che in un viaggio di andata e ritorno è l’astronauta a invecchiare di meno.
Divertitevi a ragionarci sopra, ma posso garantirvi che non fa una grinza… Ricordate sempre, però, che stiamo rappresentando il tutto nel sistema di riferimento della Terra, che è poi quello in cui si svolgono le osservazioni. L’orologio dell’astronauta rallenta perché viene riferito a questo sistema. Nulla toglie però che lui possa sentirsi fermo e osservi la Terra muoversi…
Non dannatevi troppo, però… è solo un piccolo antipasto, per i più esperti, sul quale torneremo appena ci saremo tolti “dai piedi” la relatività galileiana e legheremo in modo indissolubile la coordinata tempo con quella spazio, secondo la regola di Lorentz.
Ricordate , ancora, che il tempo appare passare più lentamente sull’astronave per chi guarda da terra, ma è un po’ come la forza centrifuga che esiste realmente anche se apparente. Il suo orologio va realmente più piano, per noi, e questo è un dato di fatto. Anche se torna a casa non può recuperare il tempo… perso, dato che ha continuato a viaggiare ad alta velocità.
QUI tutti (o quasi) gli articoli riguardanti il paradosso dei gemelli





12 commenti
Caro Enzo, come al solito ho provato a ragionare su questo articolo (bello!).
Ho quindi provato a seguire l'astronave passo, passo, per comprendere meglio cosa succede.
Il grafico sottostante, oltre a calcolare il legame tra tempo terrestre(T') e tempo (T) dell'astronave, mostra diversi punti intermedi nel percorso di andata e ritorno dell'astronave (A1, A2, A3 ….).
Le linee gialle rappresentano la luce alla sua velocità, riferite ai vari punti intermedi dell'astronave.
I numeri in giallo, quindi, indicano il tempo segnato dall'orologio terrestre visto dall'astronauta (0,5; 1, 1,5; 2; 6,5; 11; 15,5), mentre quelli verdi indicano il tempo terrestre in cui il terricolo osserva l'astronave.
I numeri rossi rappresentano il tempo terrestre (T') e quello dell'astronave (T) riferiti ai vari punti assunti dall'astronave nel suo percorso.
http://www.astrobin.com/full/38892/N/
Buona parte di quella rappresentazione, però, deriva da un ragionamento generale, che provo a descrivere.
Innanzitutto, come descritto nel grafico ho calcolato il rapporto tra Tempo astronave (T) e Tempo terrestre (T'), a proposito perchè nella figura 3 T' è sopra e T sotto?
Dopodichè, cosa accade nei vari punti che contraddistinguono il percorso dell'astronave?
Quando l'astronave è in A1, dista dalla terra 2 anni luce, per cui mentre la luce impiega 2 anni per coprire quella distanza, l'astronave viaggiando a 0,8c copre tale distanza in:
2al/0,8 = 2,5 anni Tempo Terrestre
Trasformando il tempo terrestre (T') in Tempo dell'astronave (T)
T = 0,6 T' = 0,6 2,5 = 1,5 anni Tempo Astronave
In A2 percorre 4 anni luce in:
4al/0,8 = 5 anni Tempo Terrestre
T = 0,6 5 = 3 anni Tempo Astronave
In A3 percorre 6 anni luce in:
6al/0,8 = 7,5 anni Tempo Terrestre
T = 0,6 7,5 = 4,5 anni Tempo Astronave
In A4 percorre 8 anni luce in:
8al/0,8 = 10 anni Tempo Terrestre
T = 0,6 10 = 6 anni Tempo Astronave
In A5 percorre 10 anni luce in:
10al/0,8 = 12,5 anni Tempo Terrestre
T = 0,6 12,5 = 7,5 anni Tempo Astronave
In A6 percorre 12 anni luce in:
12al/0,8 = 15 anni Tempo Terrestre
T = 0,6 15 = 9 anni Tempo Astronave
In A7percorre 14 anni luce in:
14al/0,8 = 17,5 anni Tempo Terrestre
T = 0,6 17,5 = 10,5 anni Tempo Astronave
Al rientro sulla terra ha percorso 16 anni luce in:
16 al/0,8 = 20 anni Tempo Terrestre
T = 0,6 20 = 12 anni Tempo Astronave
Già, però in ogni punto (A1, A2 …) cosa vede il terricolo e cosa vede l'astronauta?
Punto A1
Il terricolo vede l' orologio dell'astronave che segna 1,5 anni, mentre sulla Terra sono passati 4,5 anni.
L'astronauta vede l'orologio della Terra segnare 0,5 anni, mentre quello sull'astronave segna 1,5 anni.
Per il Terricolo il tempo sull'astronave scorre più lento di 1/3 (1,5/4,5).
Per l'astronauta il tempo sulla terra scorre più lento di 1/3 (0,5/1,5)
Punto A2
Il terricolo vede l' orologio dell'astronave che segna 3 anni, mentre sulla Terra sono passati 9 anni.
L'astronauta vede l'orologio della Terra segnare 1 anno, mentre quello sull'astronave segna 3 anni.
Per il Terricolo il tempo sull'astronave scorre più lento di 1/3 (3/9).
Per l'astronauta il tempo sulla terra scorre più lento di 1/3 (1/3)
Punto A3
Il terricolo vede l' orologio dell'astronave che segna 4,5 anni, mentre sulla Terra sono passati 13,5 anni.
L'astronauta vede l'orologio della Terra segnare 1,5 anni, mentre quello sull'astronave segna 4,5 anni.
Per il Terricolo il tempo sull'astronave scorre più lento di 1/3 (4,5/13,5).
Per l'astronauta il tempo sulla terra scorre più lento di 1/3 (1,5/4,5)
Punto A4
Il terricolo vede l' orologio dell'astronave che segna 6 anni, mentre sulla Terra sono passati 18 anni.
L'astronauta vede l'orologio della Terra segnare 2 anni, mentre quello sull'astronave segna 6 anni.
Per il Terricolo il tempo sull'astronave scorre più lento di 1/3 (6/18).
Per l'astronauta il tempo sulla terra scorre più lento di 1/3 (2/6)
Punto A5
Il terricolo vede l' orologio dell'astronave che segna 7,5 anni, mentre sulla Terra sono passati 18,5 anni.
L'astronauta vede l'orologio della Terra segnare 6,5 anni, mentre quello sull'astronave segna 7,5 anni.
Per il Terricolo il tempo sull'astronave scorre più lento di 1/3? 7,5/18,5 = 0,405405
Per l'astronauta il tempo sulla terra scorre più lento di 1/3 ? 6,5/7,5 = 0,8666666
Dove è finita la simmetria?
Un attimo, l'astronave ha invertito la sua rotta, per cui bisogna tenere conto di questa inversione di rotta.
Prendendo come riferimento il punto A4, prima dell'inversione di rotta, basta considerare il tempo trascorso dal punto A4.
Quindi, quando l'astronave è in A5:
Per il Terricolo mentre l'astronave si spostava da A4 ad A5 è passato solo 0,5 anno (18,5 – 18), mentre sull'astronave sono passati 1,5 anni (7,5 – 6), per cui per il terricolo il tempo sull'astronave scorre 3 volte più veloce (1,5/0,5)
Per l'astronauta sulla terra sono passati 4,5 anni (6,5 –2), mentre per lui sono passati 1,5 anni (7,5-6), per cui per l'astronauta il tempo sulla terra scorre tre volte più veloce (4,5/1,5)
Punto A6
Il terricolo vede l' orologio dell'astronave che segna 9 anni, mentre sulla Terra sono passati 19 anni.
L'astronauta vede l'orologio della Terra segnare 11 anni, mentre quello sull'astronave segna 9 anni.
Per il Terricolo mentre l'astronave si spostava da A4 ad A6 è passato solo 1 anno (19 – 18), mentre sull'astronave sono passati 3 anni (9 – 6), per cui per il terricolo il tempo sull'astronave scorre 3 volte più veloce (3/1)
Per l'astronauta sulla terra sono passati 9 anni (11 –2), mentre per lui sono passati 3 anni (9-6), per cui per l'astronauta il tempo sulla terra scorre tre volte più veloce (9/3)
Punto A7
Il terricolo vede l' orologio dell'astronave che segna 10,5 anni, mentre sulla Terra sono passati 19,5 anni.
L'astronauta vede l'orologio della Terra segnare 15,5 anni, mentre quello sull'astronave segna 10,5 anni.
Per il Terricolo mentre l'astronave si spostava da A4 ad A7 sono passati solo 1,5 anni (19,5 – 18), mentre sull'astronave sono passati 4,5 anni (10,5 – 6), per cui per il terricolo il tempo sull'astronave scorre 3 volte più veloce (4,5/1,5)
Per l'astronauta sulla terra sono passati 13,5 anni (15,5 –2), mentre per lui sono passati 4,5 anni (10,5 – 6), per cui per l'astronauta il tempo sulla terra scorre tre volte più veloce (13,5/4,5)
All'arrivo
Il terricolo vede l'orologio dell'astronave che segna 12 anni, mentre quello a Terra 20 anni.
L'astronauta vede l'orologio della Terra che segna 20 anni, mentre quello sull'astronave 12 anni
Per il Terricolo mentre l'astronave rientrava da A4 a terra sono passati 2 anni (20 – 18), mentre sull'astronave sono passati 6 anni (12 – 6), per cui per il terricolo il tempo sull'astronave scorreva 3 volte più veloce (6/2)
Per l'astronauta sulla terra sono passati 18 anni (20 –2), mentre per lui sono passati 6 anni (12 – 6), per cui per l'astronauta il tempo sulla terra scorreva tre volte più veloce (18/6)
Ovviamente i risultati ottenuti sono proprio quelli riportati nel grafico iniziale.
Vorrei però usare un punto qualsiasi come per esempio A4 unendo all'osservazione anche un ragionamento.
Quando l'astronave è in A4, il terricolo vede l'orologio dell'astronave che segna 6 anni.
Il terricolo, però, sa bene che A4 dista 8 anni luce, per cui ciò che sta vedendo in realtà è accaduto 8 anni prima (giusto il tempo impiegato dall'informazione trasportata dalla luce per percorrere quella distanza).
Ciò significa che se l'orologio della terra segna 18 anni, quello dell'astronave segnava 6 anni ben 8 anni prima, ossia a 10 anni terrestri dall'inizio del viaggio.
In pratica il terricolo può facilmente trovare la relazione tra i due diversi scorrere del tempo
6 (tempo Astronave)= 10 (tempo terrestre) x
x= 6/ 10 = 0,6
Ovviamente è proprio T = 0,6 T'
Anche l'astronauta può tranquillamente trovare la stessa relazione, dato che se la luce ci ha messo 8 anni per trasportare l'informazione dell'orologio terrestre che segnava 2 anni, ora sulla terra sono trascorsi 8 anni da quando quell'immagine è partita, per cui il tempo terrestre corrispondete è uguale a 2 + 8 = 10 anni terrestri .
Anche l'astronauta, è arrivato alla stessa conclusione.
Fin qui tutto bene, spero.
Il problema sorge quando l'astronauta guarda il suo orologio.
Dunque: ho percorso 8 anni luce, se guardo il Tempo terrestre ho impiegato 10 anni, per cui viaggiavo come previsto ad una velocità di 0,8c.
Se guardo l'orologio dell'astronave ho impiegato solo 6 anni per percorrere 8 anni luce.
Eppure sono sicuro di non aver mai superato la velocità della luce.
O si è rotto l'orologio o si è ristretto il tempo.
Paolo
caro Paolo,
devi pensare che gli osservatori non pensino... ma accettino passivamente le osservazioni. Comunque sei diventato un vero mago e, come al solito, grazie per aver individuato il mio solito errorino...
Penso che con Minkowsky andrai proprio a nozze!
Ero convinto di riuscirmi a ricavare da solo la T = T’ (1 – X2)½ attraverso pitagora ma non ci sono proprio riuscito...

Che asino....
Caro Enzo, hai ragione terricolo e astronauta si limitano ad osservare.
Perciò ho deciso di mettere a dura prova le loro osservazioni.
In pratica dopo aver raggiunto A4, l'astronave compie il suo viaggio di rientro alla velocità della luce.
Sono curioso di notare l'espressione del terricolo, che appena distoglie l'occhio dal telescopio ed annota che al punto A4 l'orologio dell'astronave segna 6 anni, si sente toccare la spalla dall'astronauta che lo informa di essere appena arrivato..... e il suo orologio segna 6 anni (sulla terra dalla sua partenza ne sono passati 18).
Per il terricolo il viaggio di rientro dell'astronave è stato istantaneo (18 anni del punto A4 – 18 anni del rientro= 0).
Per l'astronauta, nel punto A5 legge un tempo terrestre di 6 anni, in A6 10 anni, in A7 14 anni, già ma tutte queste letture avvengono nello stesso istante, dato che il suo orologio non si muove.
Nel medesimo istante l'astronauta vede tutte le posizioni dell'orologio terrestre da 2 (orologio terrestre visto in A4) a 18 anni.
Per l'astronauta il tempo terrestre scorre a velocità infinita.
Ora mi è più chiaro il concetto espresso nella parte iniziale dell'articolo.
La figura sottostante mostra quanto descritto.
http://www.astrobin.com/full/38892/O/
Mi sono anche domandato se il terricolo può vedere la posizione dell'astronave in A5, A6 o A7.
Dato che l'astronave cavalca proprio il bordo del cono di luce, essa viaggia alla stessa velocità dell'informazione, ossia della luce, per cui le informazioni in A5, A6, A7 raggiungono la terra nello stesso istante, ossia 18 anni.
Sono arrivato alla conclusione (mi sbaglio?) che il terricolo dopo l'astronave in A4, non può che rivederla ricomparire istantaneamente al rientro, le informazioni di A5, A6, A7 sono compresse nel medesimo intervallo di tempo zero (forse sarebbe meglio dire che tende a zero).
Avendo a disposizione l'Enterprise, la tentazione è stata grande, per cui ho voluto esagerare lanciandola da una velocità doppia di quella della luce.
Ora dopo 14 anni terrestri dalla partenza, l'astronauta giunge a terra e può tranquillamente osservare insieme al terricolo la sua astronave che si avvicina da A3 a A4, fino a raggiungerlo, quando l'orologio terrestre segna 18 anni.
Il tutto è mostrato in questa immagine
http://www.astrobin.com/full/38892/P/
Un'ultima considerazione, usando la formula T = T’ (1 – X^2 )^ 1/2 = T' (1 – 2^2) ^ 1/2= T' -3^ ½
si ottiene la radice quadrata di un numero negativo, che non dovrebbe esistere (un numero negativo elevato al quadrato fornisce un numero positivo), ma la formula, presumo, parta correttamente dal presupposto che X (v/c) non possa assumere valori superiori ad 1, ossia che la velocità della luce non è superabile.
Paolo
caro Paolo, mi sembra tutto perfetto fino alla velocità della luce. Tuttavia, già in quel caso siamo a un limite non raggiungibile per definizione da corpi che hanno massa. Andare oltre vuol dire non potere più usare la formula che nasce proprio dalla costanza della velocità della luce... v/c NON può essere maggiore di uno se no tutta le leggi vanno al diavolo... e il sistema di riferimento non è più utilizzabile...
Un'astronave che si trova in prossimità di una stella molto distante dal nostro sistema solare è in procinto di partire e fare ritorno sulla Terra.
Proprio nel momento esatto della partenza, l'astronauta assiste all'esplosione di una supernova distante un milione di anni luce (e quindi la supernova è in realtà esplosa un milione di anni fa ma solo adesso l'astronauta ne osserva gli effetti).
Poiché la supernova dista egualmente un milione di anni anche dalla Terra, i terrestri ne osservano adesso gli effetti luminosi.
L'astronauta, la cui astronave viaggia in moto rettilineo uniforme ad una velocità di 0.8 c (per esaminare il caso solo nell'ambito della relatività ristretta, eliminiamo l'accelerazione iniziale e la decelerazione finale), arriva sulla Terra e racconta della supernova esplosa esattamente 5.37 anni fa (quindi si deduce che il viaggio dell'astronave è durato, per l'astronauta, 5.37 anni).
La risposta dei suoi conterranei è: anche noi abbiamo assistito all'esplosione della stessa supernova, ma non è avvenuta, a causa della relatività ristretta, 5.37 anni fa, bensì...
La domanda è: quanti anni prima sulla Terra hanno assistito all'esplosione della supernova?
Più o meno di 5.37 anni?
E perché?
Si noti che la distanza della supernova (un milione di anni fa) è ininfluente; l'importante è l'equidistanza della stella dalla Terra e dall'astronave al momento della partenza di quest'ultima.
E' forse un goffo tentativo di sincronizzare gli orologi della Terra e dell'astronave, ma direi che funziona: i due orologi sono sincronizzati al momento della partenza dell'astronauta.
Si noti altresì che ci sono solo due sistemi di riferimento e, anche se in realtà la Terra è "ferma" e l'astronave è in movimento verso la Terra, entrambi i sistemi vedono sé stesso fermo e l'altro sistema avvicinarsi alla velocità del 80% rispetto a quella della luce.
Grazie infinite per la risposta.
P.S.
Ha già risposto a qualche quesito di mio fratello Giancarlo.
In realtà, la supernova non conta niente, dato che al momento della partenza i due orologi segnano lo stesso tempo, in quanto fanno parte dello stesso sistema. Tuttavia, quando l'astronauta viaggia il suo tempo si dilata e arriva a terra più giovane dei terrestri. L'astronauta una volta arrivato diventa parte del sistema terrestre e, quindi, resta più giovane. Il tempo passato dalla partenza (e quindi dal momento in cui ha visto la supernova) è per lui decisamente minore.
E' esattamente il problema che ho inserito in evidenza... dove sono considerati due gemellini.
Il succo sta tutto nella frase: "i due orologi sono sincronizzati al momento della partenza dell'astronauta.". Da quel momento in poi, però, quello dell'astronauta gira più piano... La frase è valida, comunque, se astronave e Terra sono immobili uno rispetto all'altra al momento della partenza.
Penso di avergli già risposto...
I casi sono due:
1) la Terra è "ferma" (virgolettata perché in realtà nulla è fermo nell'universo) e l'astronave viaggia verso la Terra alla velocità costante di 0.8 c, per cui i 5.37 anni dell'astronauta valgono 8.5 anni terrestri;
2) l'astronave è ferma e la Terra le si muove incontro alla velocità costante di 0.8 c, per cui i 5.37 anni dell'astronauta valgono circa 3.22 anni terrestri.
E' verissimo che quello che succede in realtà è il caso n. 1, ma è altresì vero che non esiste sistema di riferimento privilegiato.
Ammettiamo allora che i sistemi di riferimento siano sempre due; al momento della "sincronizzazione", astronave e Terra non sono nello stesso sistema di riferimento poiché, rettifico, nell'istante dell'avvistamento dell'esplosione della supernova, l'astronave viaggiava già in moto rettilineo uniforme alla velocità 0.8 c e, quando astronave e Terra si incrociano, l'astronave non si ferma ma prosegue il suo moto rettilineo uniforme.
Poiché è impossibile sincronizzare gli orologi di due sistemi di riferimento così lontani, ho usato l'escamotage della supernova equidistante da entrambi gli osservatori: è certo che l'istante X in cui avviene l'avvistamento dell'esplosione della supernova è simultaneo nei due sistemi di riferimento, così come è simultaneo nei due sistemi di riferimento l'incrocio dei due osservatori.
A questo punto, chiedo: esiste o no un sistema di riferimento privilegiato?
Grazie ancora per l'interessamento e la sollecita risposta.
scusa, ma sei tu che hai detto fin dall'inizio che gli orologi sono sincronizzati alla partenza:
"Un'astronave che si trova in prossimità di una stella molto distante dal nostro sistema solare è in procinto di partire e fare ritorno sulla Terra". Supponi, quindi, che astronave e Terra facciano parte del sistema terrestre...
In generale, ognuno dei due sistemi vede l'orologio dell'altro rallentare, ma tutto sta nel fatto che l'astronave si ferma e cambia sistema. Analoga situazione si avrebbe se un osservatore terrestre salisse "al volo" sull'astronave mentre lei passa accanto alla Terra senza fermarsi... In questo caso il più giovane sarebbe il terrestre (è lui che cambia sistema).
No, non esiste un sistema di riferimento assoluto.
L'unica differenza con il paradosso dei gemelli è che lì facciamo partire qualcuno da un punto coincidente con la Terra (e non da una certa distanza) e poi lo facciamo tornare indietro. Il cambiamento di sistema si ha quattro volte: prima della partenza, nel viaggio di andata, nel viaggio di ritorno, dopo il momento del ritorno.
Benissimo.
So come funziona il paradosso dei gemelli, che paradosso non è, e come i sistemi di riferimento siano tre per cui non c'è specularità.
Allora io, per cercare di capire meglio e per avere perfetta specularità, che ho fatto?
Ho ridotto a due i sistemi di riferimento, eliminando il viaggio di andata.
Quindi due soli sistemi di riferimento, uno fermo, la Terra (che in realtà ferma non è ma viaggia a velocità molto inferiori a c, per cui la consideriamo ferma) e uno, l'astronave, in moto rettilineo uniforme verso la Terra alla velocità di 0.8 c.
Ora cosa devo fare?
Faccio partire due timer, uno sull'astronave e uno sulla Terra, naturalmente i due timer devono partire simultaneamente e mi invento un evento che viene visto simultaneamente da entrambi gli osservatori e che viene utilizzato come sincronizzatore.
I due timer devono essere fermati naturalmente simultaneamente quando i due osservatori si incrociano.
Quindi vediamo i requisiti del problema:
- i sistemi di riferimento sono due e sono perfettamente speculari
- un sistema è fermo e uno è in moto rettilineo uniforme alla velocità di 0.8 c
- non esiste alcuna accelerazione né decelerazione dell'astronave
- non esiste alcuna partenza né arrivo: l'astronave è già in moto quando i timer sono attivati e continua a essere in moto quando i timer sono fermati
- i timer sono perfettamente sincronizzati sia nell'istante della loro attivazione sia nell'istante in cui sono fermati.
Forse nei commenti precedenti non mi sono spiegato bene ma, quando dicevo "per esaminare il caso solo nell'ambito della relatività ristretta, eliminiamo l'accelerazione iniziale e la decelerazione finale", intendevo proprio questo: sempre due sistemi di riferimento e non uno alla partenza dell'astronave e due dopo.
A questo punto, se il timer sull'astronave segna 5.37 anni, vorrei capire perché il timer sulla Terra segna 8.5 anni e non 3.22.
Da qualche parte ho letto che esiste un sistema di riferimento privilegiato che sarebbe l'universo in cui tutte le cose si muovono, mentre il sistema di riferimento dell'astronave, oltre che muoversi nell'universo insieme con l'universo, è dotato anche di moto e direzione propri dovuti ai motori e al sistema direzionale.
Ma è un'ipotesi che non mi piace per niente.
Grazie ancora e mi scuso nel caso in cui (ma sono convinto di no) il suo cervello fumi quanto il mio.
I due numeri che trovi vanno d'accordissimo. Se l'astronave si ferma vale il 5.37 ore (minore di quello terrestre). Se l'astronave prosegue chi sale segna un tempo pari a 3.22 ore. Chi cambia sistema è il più giovane e vale sempre la relazione 1/gamma....
A questo punto, comunque, ti consiglierei di riguardare gli appunti di relatività ristretta... e il significato di gamma nei due sistemi di riferimento.
stai tranquillo che non esiste sistema assoluto nella RR. Al limite erano sorti problemi con la RG tenendo in conto il principio di Mach. Ma è tutta un'altra storia....
In tempi orrendi come questi, mi sono fatto una panciata così di relatività ristretta, che considero più di una teoria, molto di più (e a darmi ragione ci sono continue verifiche che confermano quella che ormai dovrebbe essere chiamata legge).
Però mi diverte un sacco trovare casi limite in cui sia difficile trovare una spiegazione esaustiva.
Nel caso precedentemente discusso, non c'è anima viva che cambia sistema di riferimento.
I due timer sono forzatamente sincronizzati quando il fenomeno dell'esplosione della supernova viene osservato dalla Terra (che assumiamo ferma) e dall'astronauta (che si trova già in moto rettilineo uniforme alla velocità di 0.8c).
Quando l'astronave passa nelle vicinanze della Terra, i due timer vengono fermati e fotografati.
L'astronave procede nel suo viaggio alla solita velocità rettilinea e uniforme e i due osservatori continuano a restare ciascuno nel proprio sistema di riferimento: nessuno passa da un sistema di riferimento all'altro.
Le fotografie dei due timer vengono trasmesse telematicamente dalla Terra all'astronave e viceversa e Le posso assicurare che i bit, di cui sono costituite le due immagini, non invecchiano nel passaggio da un sistema di riferimento all'altro (le immagini trasmesse rimangono fedeli agli originali) e non ci interessa minimamente conoscere quanto tempo chi hanno impiegato i bit a essere trasmessi (naturalmente alla velocità della luce).
Ora mi chiedo: se la fotografia scattata sull'astronave, che viaggiava a velocità 0.8c, segna 5.37 ore, che ore segna la fotografia scattata sulla Terra che (anche se nulla è fermo nell'universo, e mi ripeto) abbiamo considerata ferma? E perché?