Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo

Bene. E’ ora di fare nuove conoscenze nel nostro teatro della fisica. La quantità di moto ci ha insegnato a giocare a bocce e a biliardo. Ci ha anche dimostrato che una ferrea volontà permette di conservarsi costante anche quando sembrano apparire forze “aliene”. Nel far questo ci ha permesso di ricavare e di ripassare i tre principi della dinamica. Niente male per una grandezza fisica così semplice.

Nel frattempo, i vettori si sono divertiti a scambiarsi favori, a sommarsi, a sottrarsi, a moltiplicasi e addirittura a crearne uno nuovo di zecca che occupa una terza dimensione rispetto agli altri due.

Che ne direste di insegnare anche alla nostra quantità di moto i giochi di prestigio dei vettori? Non dimentichiamo, infatti, che anche lei è un vettore! In particolare, è molto interessata al prodotto vettoriale. Non possiamo darle torto: abituata com’è a muoversi sempre in linea retta è ovvio che speri di visitare o -almeno- a dar luogo a qualcosa che la imiti in una diversa dimensione. Non ci resta, quindi, che descrivere come nasce questa “sua” creatura  che andrà a dominare lo spazio a tre dimensioni.

Ormai sappiamo benissimo come si calcola il prodotto vettoriale di due vettori. Basta calcolare il seno dell’angolo tra le loro direzioni e poi moltiplicarlo per i moduli dei due vettori. Sappiamo anche che per fare questa operazione non conta quale sia il primo vettore del prodotto: il modulo rimane sempre lo stesso. Anche la direzione è una e una sola: quella perpendicolare al piano individuato dai due vettori. L’ordine dei vettori è importante solo per determinare il verso del vettore finale. Per far ciò, possiamo usare la mano destra oppure rifarci all’avvitamento o allo svitamento di una vite molto speciale.

Prima di scomodare la quantità di moto, traffichiamo un po’ solo con la sua parte vettoriale, ossia con la velocità. In realtà, quello che andiamo a descrivere vale per qualsiasi vettore, ma è meglio applicarlo direttamente alla velocità. In tal modo abbiamo già fatto il primo passo.

E’ il momento del … momento

Disegniamo, allora, la Fig. 20.   Tracciamo la direzione di una certa velocità costante, ossia quello che capita in un moto rettilineo uniforme. La velocità è abbastanza stufa di agire da sola, senza nessuno spettatore che ammiri la sua banale, continua, ma fondamentale azione. E’ quindi contentissima quando un punto O, immobile, compare dal nulla e osserva il suo percorso.

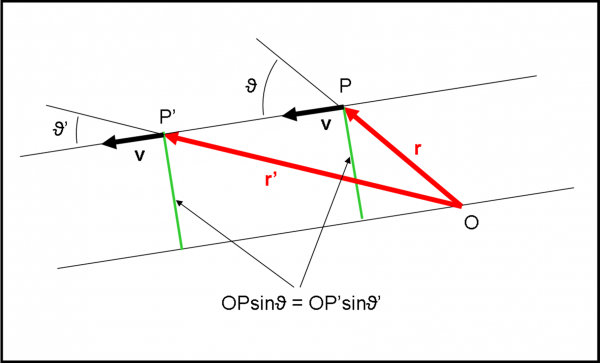
Si scambiano informazioni nel loro linguaggio (che è poi sempre quello della matematica e della geometria) e si rendono conto di una caratteristica geometrica che rimane costante nella situazione che stanno vivendo.

Qualsiasi sia  il punto di applicazione P della velocità, il segmento variabile OP moltiplicato per il seno dell’angolo tra la direzione OP e la direzione della velocità rimane sempre uguale! Beh… niente di straordinario, era facile aspettarselo dato che, in fondo, è la distanza tra la retta della velocità é la parallela ad essa che passa per O. Possiamo vedere graficamente questa banale considerazione aggiungendo nella figura un punto P’. Risulta, senza ombra di dubbio, che OP sinϑ = OP’ sinϑ’. La faccenda è sempre la stessa, qualsiasi sia la posizione raggiunta da v con O sempre fermo a osservarla (all’infinito le cose si complicherebbero un po’, ma a noi interessa ben poco dato che vogliamo introdurre qualcosa di fisicamente concreto): un bel legame tra la velocità e il punto.

OP e v decidono di sfruttare questa conclusione geometrica e decidono di creare una nuova grandezza fisica. La chiamano momento.

In realtà, la velocità, essendo un vettore, conosce bene tutte le operazioni che possono fare i vettori e, quindi, convince facilmente OP a diventare anch’esso un vettore. Non è qualcosa di nuovo, dato che la distanza tra due punti è stata spesso e volentieri considerata un vettore. Oltretutto –state bene attenti!– la variazione della distanza OP al variare di P, in funzione del tempo, è qualcosa di molto ben conosciuta dalla velocità. Non è altro che lei stessa! Se chiamiamo r il vettore OP, si ha proprio che v = dr/dt. In fondo dr è proprio lo spazio percorso dal punto di applicazione della velocità lungo la sua retta. Non dovrei nemmeno perderci del tempo, ma basta fare, in Fig. 21, la differenza dei vettori r(t + dt), ossia OP’, e r(t), ossia OP, per trovare che la loro differenza è proprio il vettore dr.

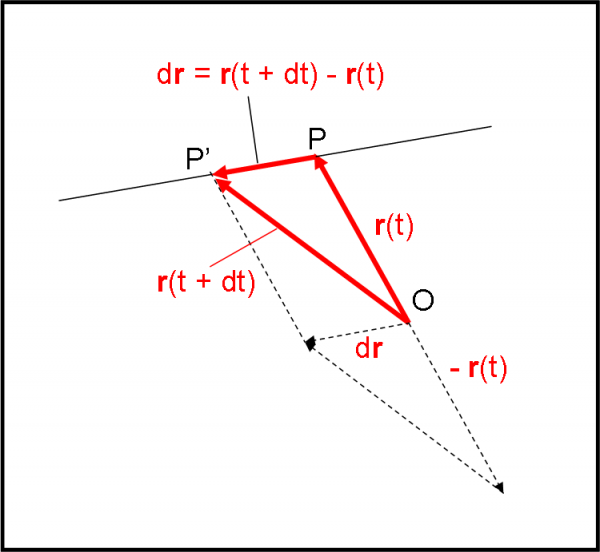
Introduciamo, allora, questa nuova grandezza momento h, che è il prodotto vettoriale tra r e v, ossia h = r Λ v. Scritto in questo modo, indica anche il verso del vettore h. Basta usare la regola della mano destra o quella delle “vite”. Nel caso della Fig. 22, il verso è quello che va verso l’alto.

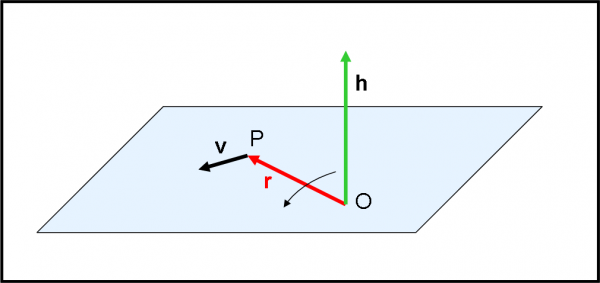
Tuttavia, prima di pensare al verso, pensiamo al modulo. Esso vale, indipendentemente da quale vettore si mette per primo:

h = r v sinϑ

Un attimo, un attimo… Abbiamo appena dimostrato geometricamente che la grandezza scalare r sinϑ è costante al variare della posizione del punto di applicazione P del vettore v che percorre una linea retta. Ne segue, facilmente, che:

h = costante

Il modulo del momento di un vettore costante, che si muove di moto rettilineo, è una costante. Il modulo è costante, ma è anche costante la direzione e il verso del vettore momento. Possiamo tranquillamente dire che il vettore h è costante. Ovviamente, dobbiamo sempre aggiungere rispetto a quale punto è calcolato e quindi h si chiama momento di un vettore rispetto a un punto fisso O.

Non vi è piaciuto il modo con cui abbiamo dimostrato la costanza di questa grandezza vettoriale? Troppo geometrica? Troppa trigonometria? Bene, otteniamo lo stesso risultato attraverso un po’ di matematica….

Usiamo, nuovamente, la Fig. 20. Il vettore r’ = OP’ non è altro che la somma di due vettori: r = OP e PP’. Possiamo allora scrivere:

r’Λ v = OP’Λ v = (OP + PP’)Λ v = OP Λ v + PP’ Λ v

Ma, attenzione! PP’ e v sono paralleli e, come ormai sappiamo benissimo, il prodotto vettoriale di due vettori paralleli è uguale a zero.  Ne consegue:

r’Λ v = OP Λ v = r Λ v

Esattamente quello che volevamo dimostrare!

Una conclusione veramente ovvia che, però, spesso non viene abbastanza evidenziata nei libri… Eppure questa costanza è proprio fondamentale per far decidere alla quantità di moto di dar vita alla sua nuova creatura. Una grandezza costante non può che dare origine a una’altra grandezza costante. Ormai, il passaggio da momento vettoriale a momento angolare è di un’ovvietà puerile.

Momento angolare o momento della quantità di moto: una creatura perfetta

La velocità si è accorta che il suo momento rispetto a un punto fisso O è una costante. Non resta che proporlo alla quantità di moto che è un vettore, costante come lei. La quantità di moto ne è entusiasta e annuncia la nascita di una sua creatura costante come lei: il momento angolare rispetto a un punto O. Esso non è altro che il prodotto vettoriale tra la distanza rispetto al punto O e il vettore quantità di moto. In parole matematiche, se q = mv, il momento angolare rispetto ad O è definito da:

L = r Λ q = r Λ mv

Con:

L = r mv sinϑ

Cosa ci dice, in pratica, questa nuova grandezza (costante)? Se un certo oggetto di massa m (costante) si muove di moto rettilineo uniforme esso crea, insieme al punto O di riferimento, un vettore costante diretto secondo la regola della mano destra. Questo vettore può essere, ovviamente, applicato in O. Per come è stato costruito potremmo anche chiamarlo (forse più correttamente) momento della quantità di moto. Sicuramente ci fa capire molto meglio con chi abbiamo a che fare.

Come varia questo momento angolare, nello spazio? Innanzitutto, la direzione è sempre perpendicolare al piano dei due vettori e il verso segue la regola della mano destra. Se la retta è più distante dal punto O il momento aumenta il suo modulo, a parità di velocità: interessante, molto interessante; se la velocità aumenta,  aumenta anche il momento angolare (sempre come modulo): la cosa più ovvia, forse; se aumenta il seno dell’angolo ϑ tra i due vettori, aumenta ancora il modulo del momento angolare.

Quest’ultima situazione è particolarmente importante e da studiare più a fondo. Notate, innanzitutto che non ci interessa come vari l’angolo, ma come vari il suo seno. Il seno è una funzione (la conosciamo bene e l’abbiamo studiata a fondo nella relativa lezione di “Matematica”), che raggiunge il valore massimo per un angolo uguale a 90°. Questo ci dice che a parità di distanza OP e di velocità v, si ottiene il massimo valore del modulo del momento angolare se la direzione della velocità è perpendicolare alla direzione OP.

In parole matematiche il valore del modulo del momento angolare, uguale a r mv sinϑ, ha come valore massimo la quantità m v r (sin ϑ = 1).

Questo fatto ci ricorda qualcosa che avevamo eseguito per vedere come girava la “vite” del prodotto vettoriale. Proviamo a scomporre il vettore velocità v, punto per punto, in  due componenti: una radiale (v_R) e una perpendicolare (v_T). Eseguiamo il solito prodotto vettoriale che ci regala il momento del vettore:

r Λ v = r Λ (v_R + v_T) = r Λ v_R + r Λ v_T

Ma, r e v_R sono paralleli e quindi r Λ v_R = 0. Ne segue:

r Λ v = r Λ v_T

Questo “esercizio” vettoriale ci porta a dire che per ottenere il momento di un vettore non è necessario utilizzare tutto il vettore, ma basta considerare solo la sua componente perpendicolare al vettore r.

Qualcuno potrebbe dirmi: “Beh? Perché tanta fatica se conosciamo il vettore v?”. Avrebbe sicuramente ragione… Tuttavia, il ragionamento di prima ci conduce a una conseguenza di importanza enorme. Pensiamo, solo per un attimo, a cosa succederebbe se il vettore v non si muovesse in linea retta, ma descrivesse una curva con il modulo della velocità, v, costante.

Gira e rigira...

D’accordo, la sua quantità di moto cambierebbe da punto a punto come direzione (il moto non sarebbe più rettilineo uniforme), ma manterrebbe lo stesso modulo mv. E se il moto fosse proprio circolare con centro in O? Ossia se r fosse costante? Anche il modulo del momento rimarrebbe costante, dato che r è costante, lo è v, ma soprattutto il seno dell’angolo sarebbe sempre uguale a 1, ossia il modulo finale del momento sarebbe soltanto e sempre v r.

Nel caso della quantità di moto, dato che la massa è costante, sarebbe analogamente costante il suo modulo e anche quello del momento angolare rispetto a O. Tuttavia, c’è un vantaggio in più. Il vettore quantità di moto NON sarebbe costante, dato che cambia di verso e direzione istante per istante, mentre il vettore momento angolare rimarrebbe costante, dato che la sua direzione e il suo verso rimangono inalterati durante il moto.

In parole povere, in un moto circolare uniforme NON si conserva la quantità di moto, ma si conserva il momento angolare. Immaginiamo di vedere questo vettore che punta verso di noi (o in verso opposto se la rotazione avviene al contrario) e che rimane costante mentre la massa m gira attorno ad O. E’ o non è un segnale importantissimo per sapere cosa sta avvenendo al nostro oggetto? E’ o non è una grandezza MOLTO esplicativa? Accidenti, la nostra amica q = mv si è scelta un ottimo “figliolo”: se non può conservarsi lei si conserva il momento angolare!

Ma c’è di più… la quantità di moto non si conserva perché esiste una forza F che agisce continuamente sull’oggetto di massa m e questa forza non è altro che quella centripeta. Tuttavia, sembra che l’esistenza di questa forza non dia nessun fastidio al momento angolare. Lui rimane costante… Come mai? Beh… la risposta è facile: la forza F è sempre parallela al raggio r.

Sono andato volontariamente un po’ avanti, per farvi già sentire il “profumo” dei moti rotazionali e l’importanza del momento angolare. La prossima volta torneremo indietro e descriveremo l’ultima parte con maggiore calma. Tuttavia, il succo e il valore indiscusso del momento angolare si sono già manifestati in pieno.

Complimenti quantità di moto! Hai costruito una creatura meravigliosa…