Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica.

Come poter agire per evitare una catastrofe senza speranza per le specie viventi terrestri? Basta unire gli sforzi!

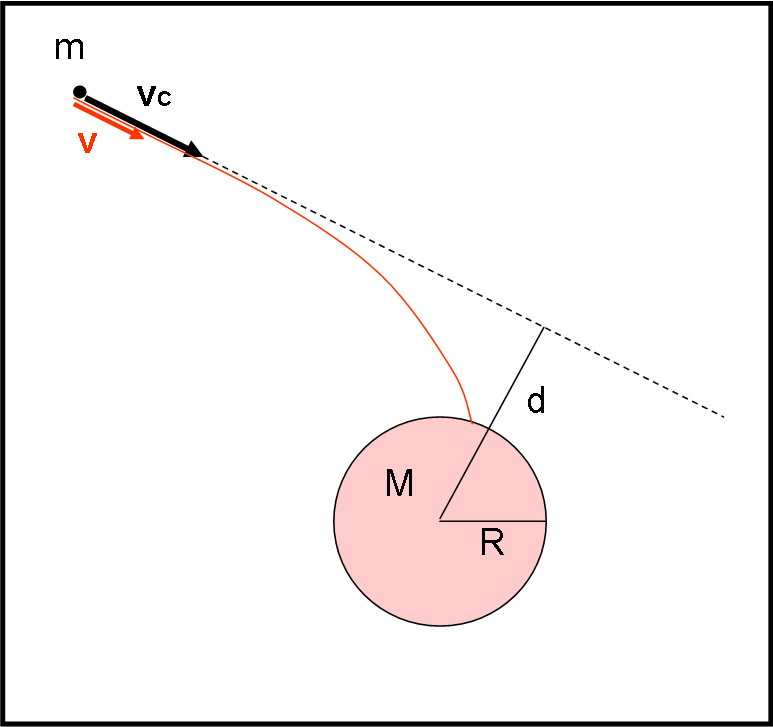
Un asteroide di circa 20 km è in rotta di collisione con la Terra. Sfortunatamente, la sua velocità non è elevata e, tenendo conto del contributo che la gravità del pianeta impartisce alla traiettoria del piccolo corpo planetario, la catastrofe sembra imminente.  Il suo parametro d’impatto d non lascia speranze.

N.B.: Il parametro d’impatto è la distanza (misurata perpendicolarmente) tra la direzione del moto dell’asteroide a grande distanza  (tale da non risentire della gravità terrestre) e il pianeta.

Tuttavia, i governi terrestri uniscono velocemente le proprie forze  per cercare di aumentare la velocità v dell’asteroide. Per far ciò devono calcolare la velocità minima v_C che permetterebbe all’asteroide di sfiorare soltanto la Terra e poi proseguire nella sua corsa sfrenata (anche a costo di sradicare qualche albero troppo alto…). La Fig. 1 mostra la situazione, in cui la curva rossa è la traiettoria prevista senza aver corretto la velocità originaria v.

L’impresa riesce perfettamente attraverso una serie di manovre di “spinta”, ottenute utilizzando tutti i missili terrestri (viva la fantasia!).

Calcoliamo, perciò la velocità minima v_C dell’asteroide, necessaria per scongiurare “al pelo” l’impatto catastrofico. Il diametro dell’asteroide può essere tranquillamente trascurato…

Consideriamo inesistente l'atmosfera terrestre

Disegniamo la Fig. 1, con la traiettoria dell’asteroide che sfiora letteralmente la Terra.

Quando l’asteroide si trova molto lontano con velocità (corretta) v_C, il suo momento angolare rispetto alla Terra è:

I_L = m v_C d

L’unica forza che agisce sull’asteroide è la forza di gravità della Terra, ma essa passa per il suo centro, per cui non aggiunge alcun momento. Ne segue che durante tutto il tragitto il momento angolare dell’asteroide deve rimanere costante (conservazione del momento angolare). In  particolare, nel momento di tangenza, vale:

I_T = m R V

Abbiamo la prima relazione:

m v_C d = m R V

ossia:

V = v_C d/R     …. (1)

Durante il viaggio, però si deve conservare anche l’energia totale. Quando l’asteroide è lontano l’energia è solo cinetica, ossia abbiamo:

E_L = ½ m v_C²

Quando l’asteroide arriva al punto di tangenza la sua energia è sia cinetica che potenziale, dovuta alla gravità terrestre. Abbiamo allora:

E_T = ½ mV² – GMm/R

La conservazione ci impone che:

½ m v_C² = ½ mV² – GMm/R

Ossia:

V² = v_C² + 2GM/R     …. (2)

Uguagliando (1) e (2) si ottiene subito il valore necessario di v_C:

v_C² d²/R² = v_C² + 2GM/R

v_C²(d²/R² -1) = 2GM/R

v_C² = 2GM/(R(d²/R² -1)) = 2GM/(R(d² – R²)/R²) = 2GMR/(d² – R²)

v_C = (2GMR/(d² – R²))^1/2

Un semplice problemino che potrebbe anche attivare molte altre variazioni sul tema...