La figura tracciata nel piccolo quiz stile Halloween è completamente sbagliata. Ma l'errore è difficile a vedersi e normalmente si pensa subito ai vari triangoli uguali facendosi trarre in inganno. L'errore  sta invece proprio all'inizio di tutto: bisettrice di un angolo e asse del lato opposto non possono mai trovarsi nella posizione indicata in figura. Tuttavia, scegliendo un triangolo un po' particolare si cade nell'assurdo senza errori facilmente visibili.

Francesco, come al solito, è arrivato alla conclusione e prometteva anche una spiegazione. Io ne regalo una molto semplificata, ma più che sufficiente per un problemino piuttosto "stupido". Dato che si diceva di prendere un triangolo qualsiasi, nulla ci vieta di prenderne uno rettangolo. Il diagramma che segue mostra subito l'impossibilità di avere due triangoli uguali entrambi all'esterno del triangolo iniziale.

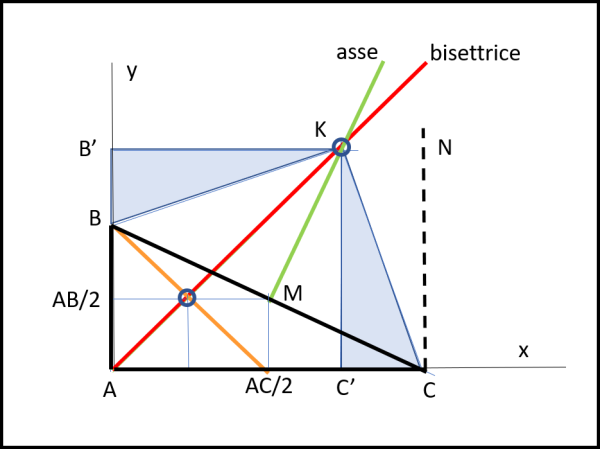
Il punto di mezzo del lato BC si trova immediatamente considerando i punti (0, AB/2) e (AC/2, 0), mentre la bisettrice è la retta rossa y = x. Basta tracciare la perpendicolare verde a BC dal punto M e si ottiene subito l'asse e il punto K. Potete allungare e stringere il triangolo di partenza o far diventare cateto maggiore il lato AB e troverete sempre che i triangoli rettangoli KBB' e KCC' sono veramente uguali, ma... (come ha detto anche Francesco) C' sarà sempre interno al triangolo ABC e B' sempre esterno (o viceversa).

Provate pure quanto volete, ma K non potrà mai superare la linea tratteggiata CN. Vi è un solo caso in cui K perde di significato, in quanto la bisettrice coincide con l'asse, ma in questo caso abbiamo proprio un triangolo isoscele (quello con l'ipotenusa arancione).

Non vale certo la pena di scrivere dimostrazioni analitiche, trattandosi solo di un... errore di sbaglio.

Scherzetto!