Questo è il primo articolo che vuole descrivere un "principio" (che, in realtà, tale non è) conosciuto da tutti, ma che spesso viene enunciato in modo quasi automatico, senza -forse- comprendere del tutto la sua logicità e le sue sfaccettature. Sto parlando del principio di Archimede e della spinta che ogni corpo riceve verso l'alto se immerso in un fluido. Per iniziare, vediamo come dovrebbe veramente essere considerato e come la sua descrizione vada di pari passo con la prima vera prova scientifica della sfericità della Terra.

Abbiamo parlato di Terra Piatta e di Terra Sferica da poco tempo (QUI), divertendoci un poco con i terrapiattisti e con le loro stramberie, figlie di un secolo che sta perdendo la capacità di studiare, di imparare e di riflettere. Come già accennato, l'idea della Terra sferica risale ai popoli più antichi e i grandi filosofi e pensatori greci lo avevano quasi coralmente considerato un dato di fatto. La scomparsa delle navi oltre l'orizzonte, la forma stessa della Luna e del Sole, ecc. davano evidenze osservative tali che non c'è certo da stupirsi se Eratostene e il suo dromedario si fidassero ciecamente di un'ipotesi da tutti accettata anche se mai veramente dimostrata in modo SCIENTIFICO (oggi le cose sembrano ben diverse... evviva l'evoluzione del cervello umano!).

Per avere la prima dimostrazione dobbiamo aspettare Archimede, che proprio studiando il galleggiamento dei corpi riesce a dare una prova decisiva e geniale.  Tutto parte dal vero principio che ha come ricadute dirette sia la spinta ricevuta dai corpi immersi in un fluido sia la sfericità della Terra. A questo riguardo, ricordiamo che il PRINCIPIO scientifico è un qualcosa che non si deve dimostrare, ma che parte dall'evidenza dei fatti. Da esso nascono diverse conseguenze che possono essere dimostrate utilizzandolo.  Sarebbe molto più corretto chiamare queste conseguenze TEOREMI. Ne segue che il celebre Principio di Archimede dovrebbe essere enunciato come Teorema di Archimede.  Potrebbe sembrare un discorso pignolo e inutile, ma tale non è, se non altro perché dimostra l'infinita grandezza del genio siracusano che non si è certo fermato a questa trattazione... basterebbe ricordare le leve, gli specchi ustori e mille altre scoperte di importanza fisica eccelsa.

Scriviamo, allora, in modo più comprensibile e semplice il vero Principio di Archimede:

Due porzioni contigue di fluido (poste alla stessa altezza rispetto alla superficie del fluido) non sono in equilibrio se sulla loro compressione agiscono forze di diversa intensità, ossia se le relative colonne di fluido sovrastanti ciascuna porzione sono di diversa altezza; la misura della compressione è quindi data dall’altezza di dette colonne, a patto che il fluido non sia compreso in qualcosa e compresso da qualcos’altro.

In questa frase ci sono risvolti a dir poco eccezionali: primo fra tutti l'idea della gravità, di una forza diretta verso il basso e, più esattamente, verso il centro della Terra; subito dopo la definizione di compressione che prenderà in seguito il nome di pressione; infine, il finale della frase che sembrerebbe poco importante e che invece fa perfettamente capire come il problema  dei vasi comunicanti fosse già ben conosciuto.

Traduciamo ancora meglio quanto detto. Se abbiamo una particella di fluido che è maggiormente compressa rispetto alla sua adiacente, viene a mancare l'equilibrio e si assiste un movimento verso la particella meno compressa. Beh... un'evidenza sotto gli occhi di tutti: un fluido sotto pressione tende a dirigersi verso zone a bassa pressione. Compressione che è totalmente dovuta alla colonna di fluido sovrastante che altro non è che la legge di Stevino (di cui parleremo in seguito) e che fa uso della forza di gravità. Tutto ciò avviene a patto che non vi siano altre costrizioni al possibile movimento del fluido, come un ostacolo naturale (ad esempio un tubo) o una forza esterna diversa da quella puramente gravitazionale.

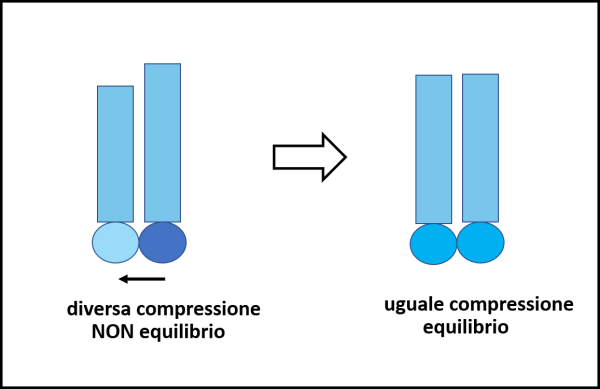
Immaginiamo in Fig. 1 due particelle di liquido, che siano compresse in modo diverso. La più compressa spinge quella meno compressa fino a che non si raggiunga l'equilibrio (ovviamente bisogna tener conto anche delle particelle limitrofe). La compressione è evidenziata dalla colonna di fluido che le sovrasta. Scusate la banalità della figura, ma è essenziale partire con il piede giusto fin dall'inizio, anche semplificando al massimo.

Vediamo subito in Fig. 2 come questa semplice constatazione porti al fenomeno dei vasi comunicanti.

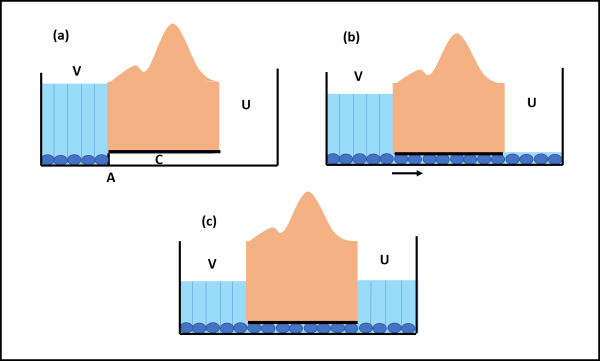
In (a) abbiamo una vasca V piena d'acqua in perfetto equilibrio (tutte le colonne sono uguali). Vi è un condotto (tubo) C in cui le pareti costringono le particelle che non risentono della colonna di materia sovrastante: il fluido (per adesso solo aria) è COMPRESO IN QUALCOSA (vedi principio, parte finale) e quindi poco importa la materia esterna al tubo. Una paratia A le separa dall'acqua contenuta in V.

In (b) solleviamo la paratia A. Le particelle di V sono più compresse e, quindi, spingono le particelle di aria verso U. Il tubo C si riempie di particelle di acqua che rimarrebbero in equilibrio tra loro (dato che non sono compresse dalla colonna sovrastante), ma che vengono continuamente spinte verso U dalle particelle di V che con loro hanno buon gioco.

In (c) le particelle di acqua che sono arrivate in U subiscono la stessa compressione delle particelle di V. Si è raggiunto l'equilibrio totale. Non è pensabile che l'acqua in U raggiunga un livello superiore, dato che a questo punto il processo si invertirebbe. Le particelle di V e di U hanno tutte la stessa compressione dovuta alla colonna d'acqua che le sovrasta, mentre le particelle nel tubo sono anch'esse in equilibrio dato che SONO CONTENUTE IN QUALCOSA (tubo) che rende ininfluente la colonna sovrastante. Se vogliamo, possiamo anche dire che esse sono mantenute in equilibrio in quanto COMPRESSE in ugual modo sia a destra che a sinistra.

Il fenomeno dei vasi comunicanti era già ben conosciuto nell'antica Grecia, ma Archimede ne dà una dimostrazione veramente scientifica, basandosi sul suo principio.

Altrettanto banale è la dimostrazione della spinta verso l'alto su un corpo immerso nell'acqua, Esso diventa un teorema, in quanto si dimostra con il principio della compressione. Lo possiamo raffigurare in modo estremamente qualitativo nella Fig. 3, riservandoci di dare spiegazioni quantitative nel proseguo degli articoli. Non credete, però, che Archimede sia stato solo qualitativo... le sue conclusioni sono state affiancate da precise quantificazioni.

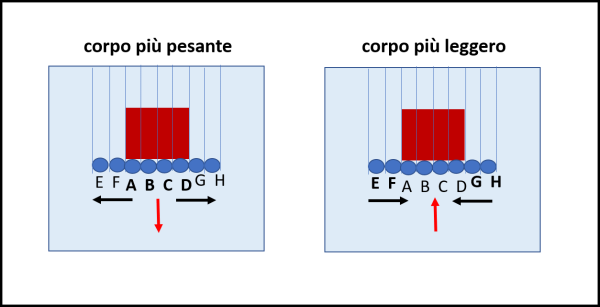
A sinistra, immergiamo nell'acqua un corpo che è più pesante della stessa. Cosa succede intorno al bordo più basso del corpo? Lungo tutta la linea d'acqua sottostante vi sono particelle di fluido con relative colonne sovrastanti che le comprimono. Tuttavia, la compressione su quelle a contatto con il fondo del corpo immerso è maggiore, in quanto la colonna sovrastante contiene sia acqua che materiale più pesante dell'acqua. Queste particelle, perciò, non si trovano in equilibrio con quelle che sono compresse da colonne di sola acqua. La conseguenza è un moto di  quelle più compresse verso quelle meno compresse e si crea un "vuoto", sotto al corpo che scende. In altra parole, l'acqua sottostante si fa da parte e crea lo spazio per la caduta del corpo.

A destra, consideriamo un corpo più leggero dell'acqua. Il discorso si inverte e sono adesso le particelle esterne al corpo che si muovono, accumulandosi sotto il corpo e creando così una barriera che lo costringe a tornare verso l'alto. E' anche ovvio che vi sono fasi intermedie, tra cui quella classica di un corpo che pesa come l'acqua.

Tra le righe si legge benissimo la consapevolezza del peso specifico dei materiali e si ha una chiara dimostrazione del perché ciò che conta è il peso del liquido spostato, dato che è proprio l'acqua che agisce sul corpo permettendogli o vietandogli la discesa.

Questa è una trattazione estremamente qualitativa, ma la riprenderemo con maggiore precisione in seguito, accorgendoci, però, di quanto una trattazione fisica "moderna" coincida quasi perfettamente con quanto dimostrato da Archimede. Vale la pena anche ricordare nuovamente come la "compressione", ossia la odierna pressione, sia un'anticipazione perfetta della legge di Stevino, che si basa proprio sulla colonna di fluido sovrastante la particella considerata.

Passiamo infine alla dimostrazione del teorema più stupefacente, ossia quello che dimostra come la Terra DEBBA essere una sfera.

Innanzitutto, con una precisione da orologiaio della fisica, Archimede trasporta un problema a tre dimensioni in uno a due dimensioni (meriterebbe leggere o quantomeno immaginare le sue figure contenute nel Libro I dei corpi fluttuanti) e poi ragiona per assurdo, come mostrato in Fig. 4.

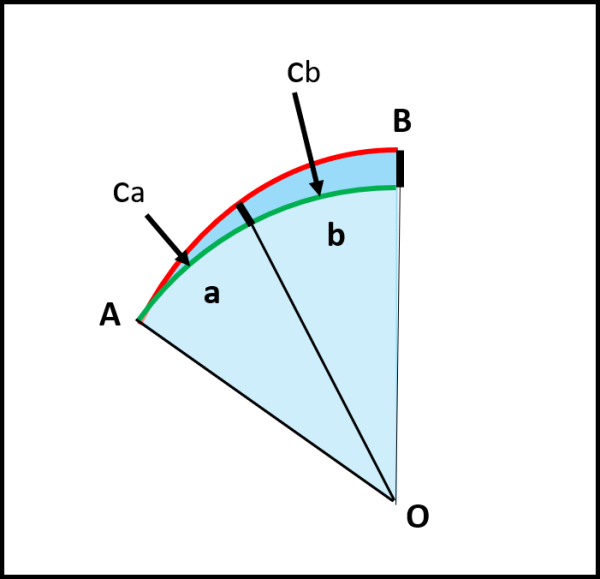
Prima di procedere, dobbiamo ricordare che a quei tempi si era già a conoscenza di quello che oggi chiamiamo baricentro o centro di massa. Esso prendeva il nome di CENTRO DEI PESI ed era rappresentato dal centro della Terra supposta (da molte evidenze) sferica. Inoltre, si supponeva che la Terra fosse all'origine completamente fluida e che solo in un secondo tempo parte della superficie si sarebbe solidificata. Da ciò derivava la convinzione che il mare riproducesse la forma primigenia e che la terraferma  riproducesse, con qualche imperfezione locale (montagne), la stessa forma. Era, quindi, ovvio e corretto riferirsi solo alla superficie liquida.  Archimede dice (con parole mie...): "Immaginiamo per assurdo che la Terra, ossia la superficie marina, non sia una superficie sferica (linea rossa). Questo comporta che le distanze tra A e O e tra B e O sono diverse, per definizione di cerchio. Con raggio AO tracciamo la circonferenza verde e consideriamo i due settori circolari a e b. Il settore b ha una compressione, dovuto alla massa d'acqua sovrastante, maggiore di quella di a (poco importa cosa ci sia sotto la superficie verde), da cui ne deriva che il settore b non è in equilibrio con il settore a e ci deve essere uno scorrimento di b verso a. In poche parole il mare dovrebbe muoversi costantemente verso una direzione. Dato che questo non capita e che la superficie marina è in equilibrio in ogni sua parte, la Terra non può che essere sferica".

Banale, ovvio, ... no, direi veramente geniale e un vero caposaldo della fisica!

Reso il giusto onore ad Archimede, la prossima volta inizieremo il percorso più "moderno"...

Terrapiattisti, che magari utilizzate il teorema di Archimede per i vostri lussuosi panfili, leggete Archimede e imparate... e, già che ci siete, leggete anche QUI, così scoprirete perché non sarebbe così comodo vivere su una Terra piatta...

 

Gli altri articoli dedicati al Teorema di Archimede li trovate QUI