Questo articolo è stato inserito nella sezione d'archivio "Antichi Greci, che passione!"

Una formula forse troppo spesso dimenticata che vede una piccola lotta "storica" tra Archimede ed Erone di Alessandria (con qualche infiltrazione cinese). Richiamiamola in quanto può essere di grande aiuto per il quiz sul mostro.

Noi lo chiamiamo Erone, ma più propriamente si dovrebbe chiamare Heron o anche Hero. Vissuto dal 10 al 70 d.C. viene considerato uno dei più grandi sperimentatori dell'antichità, passando dalla meccanica all'idraulica e via dicendo. La sua fama, però, è legata soprattutto a una formula matematica, forse non molto conosciuta, ma di utilità enorme. In realtà, si dice  che forse la paternità della formula sia da attribuire addirittura ad Archimede, vissuto due secoli prima, ma... Archimede è già così famoso che mi permetto di fare il tifo per il nostro Hero. In modo del tutto indipendente, anche i cinesi arrivarono a una formula analoga.

Scriviamola per farla ricordare a chi l'ha dimenticata:

A = √(s(s-a)(s-b)(s-c))

Che tradotta in parole dice:

Dato un triangolo qualsiasi, è sempre possibile determinare la sua area dalla conoscenza dei suoi tre lati. Se A è l'area cercata  e a, b e c sono i  lati, basta calcolare il semiperimetro s del triangolo e poi estrarre la radice quadrata del prodotto tra il semiperimetro e le differenze tra il semiperimetro e i tre lati. Il risultato è proprio l'Area cercata.

Il teorema si può dimostrare in vari modi, soprattutto utilizzando la trigonometria. Tuttavia, noi preferiamo esporre il metodo che fa uso del solo teorema di Pitagora, tanto per restare legati all'epoca storica, e qualche trucchetto di algebra.

Prendiamo un triangolo qualsiasi e chiamiamo a, b e c i suoi tre lati, come in Fig. 1.

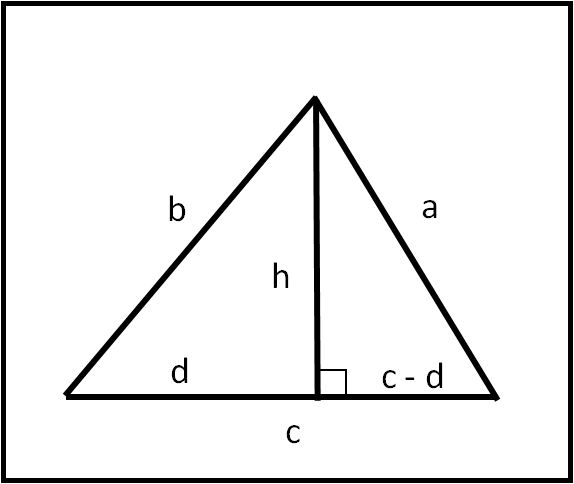
Tracciamo l'altezza h relativa al lato c. Esso sarà diviso nei segmenti d e (c-d)

Cominciamo con applicare il teorema di Pitagora ai due triangoli rettangoli così ottenuti:

b² = h² + d²                                .... (1)

a² = h² + (c-d)²

a² = h² + c² + d² -2cd              .... (2)

Ricaviamo h² + d² dalla (1) e dalla(2) e uguagliamo ...

h² + d² = b²

h² + d² = a² - c² +2cd

b² = a² - c² + 2dc

Ricaviamo d:

d = (b² - a² + c²)/2c

ed eleviamo al quadrato:

d² = (b² - a² + c²)²/4c²

Riprendiamo la (1)  ricavando h² e sostituendo il valore di d trovato

h² = b² - d² = b² - (b² - a² + c²)²/4c² = (4c²b² - (b² - a² + c²)²)/4c²

A questo punto ricordiamo uno dei più usati prodotti notevoli:

(A + B)(A - B) = (A² - B²)     .... (3)

Nel nostro caso:

A² = 4c²b²

B² = (b² - a² + c²)²

Ossia

A = 2cb

B = (b² - a² + c²)

Per cui, dalla (3)

4c²b² - (b² - a² + c²)² = (2cb + b² - a² + c²)(2cb - b² + a² - c²)

E, infine, inserendo nell'espressione di h²:

h² = (4c²b² - (b² - a² + c²)² )/4c²= (2cb + b2 - a2 + c2)(2cb -b2 + a2 - c2))/4c2

Notiamo che i termini in grassetto (sia nero che rosso) non sono altro che due quadrati

2cb + b² + c² = (b + c)²

2cb - b²  - c² = - (b - c)²

Andiamo a sostituirli nella espressione di h²

h² = ((b + c)² - a² )( - (b - c)² + a²)/4c2

Abbiamo  ben due prodotti notevoli come quello appena utilizzato:

(b+c)² - a² = (b + c -a)(b + c + a)

a² - (b-c)² = (a + b - c)(a - b + c)

Andiamo a sostituirli nella espressione di h²

h² = (b + c + a)(b + c - a)(a - b + c)(a + b - c )/4c²

Eseguiamo un piccolo trucchetto, aggiungendo e togliendo a nella seconda parentesi del secondo membro, b nella terza e c nella quarta parentesi del secondo membro:

h² = (b + c + a)(b + c - a + a - a)(a - b + c + b - b)(a + b + c + c - c)/4c²

Sappiamo, però, che a + b + c = p (perimetro), per cui:

h² = p(p - 2a)(p - 2b) (p -2 c)/4c²

Il perimetro p è, ovviamente, uguale a 2s (dove s è il semiperimetro), ossia:

h² = 2s(2s -2a)(2s -2b) (2s -2c)/4c² = 2s · 2(s-a) · 2(s-b) · 2(s-c)/4c² = 16 s (s-a)(s-b)(s-c)/4c² = 4 s(s-a)(s-b)(s-c)/c²

h = 2 √(s(s-a)(s-b)(s-c))/c             .... (4)

Il gioco è finito, in quanto sappiamo che l'area del triangolo è dato dal prodotto tra base e altezza diviso per 2, ossia:

A = c · h/2

Sostituendo in questa espressione la (4), abbiamo finalmente:

A = c · 2 √(s(s-a)(s-b)(s-c))/2c

semplificando:

A = √(s(s-a)(s-b)(s-c))

c.v.d.

Questa formula vale per qualsiasi triangolo e importa poco se le lunghezze dei lati siano o non siano numeri interi... però Hero, il nostro eroe, non si è accontentato...

 

Questo articolo è stato inserito nella sezione d'archivio "Antichi Greci, che passione!"