Quiz: Un grafo con sei vertici **/***
Continuiamo nel nostro viaggio alla scoperta di Ramsey, ma questa volta con un quiz. Nell'ultimo articolo, che trovate qui, abbiamo dato la definizione di grafo completo. Abbiamo poi dimostrato che in un grafo completo con 5 vertici, non sempre esiste un triangolo monocromatico, qualsiasi sia la colorazione dei lati. Lo abbiamo dimostrato con un semplice esempio, comunque lo riporto così come è scritto nell'articolo :
" in esiste sempre, qualsiasi sia la colorazione, un triangolo monocromatico, ovvero un sottografo con tre vertici? La risposta è no basta guardare la figura seguente:"
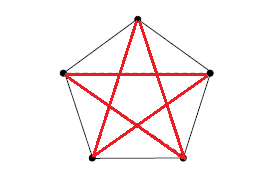
E in ?
In realtà, quello che ho scritto nell'ultimo articolo, non è un prerequisito necessario per risolvere il quiz. Per chi è ostica la parola grafo, la sostituisca con "figura composta da punti e lati che li collegano". Qui la teoria dei grafi non serve a niente.
A scampo di equivoci, e per chi non avesse letto bene l'articolo citato, e per evitare incomprensioni, il quiz è il seguente:
Chiamiamo un grafo completo con 6 vertici, ovvero un grafo in cui ogni vertice è collegato con tutti gli altri. E' vero o falso che, comunque colorando i lati del grafo con due colori, esiste sempre un triangolo monocromatico contenuto in esso?
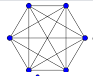
(da questo poi dedurremo poi che ogni colorazione con due colori di un grafo completo con almeno sei vertici contiene un
triangolo monocromatico).
Chiaramente potete risolverlo con il metodo che più vi aggrada. Questa volta niente angoli e niente geometria. Il problema è di tipo topologico, ovvero non dipende da come sia fatto il grafo, l'importante è che abbia 6 vertici e che siano tutti collegati fra loro. Nessun calcolo, solo pensiero allo stato puro.






13 commenti
Aggiungo il sesto punto al centro della figura del grafo con 5 vertici
Ora collego il nuovo punto al vertice 1 con un lato nero . Per evitare di avere un triangolo con lati dello stesso colore, devo collegare il centro a al punto 2 con un lato rosso. Per lo stesso motivo sono costretto a collegare il punto 4 con un lato nero.
Ora però se collego l'ultimo punto, il 5 con un lato rosso si forma il triangolo monocromatico rosso tra i punti 5 2 e il centro. Ma se uso un lato nero si forma un triangolo monocromatico nero tra i punti 5 1 e il centro.
In ogni caso avrò un triangolo monocromatico.
si Maurizio, ma in questo caso. Il quiz è "qualsiasi sia la colorazione" non in specifico quella del disegno.
spero di averlo scritto bene, ma è così anche nel testo.
Ho scelto deliberatamente di costruire il grafo K6 partendo proprio da quella configurazione di K5 perché è una configurazione che non presenta già in partenza triangoli monocromatici.
Altrimenti ne esisterebbe già uno.
Il precedente commento ammette una variante intermedia che comunque porta alla stessa conclusione
Riassumo le due varianti
Mi sembra che l'idea di un approccio incrementale dovrebbe essere valida, nel senso che scelgo come punto di partenza una configurazione che mi garantisce di non avere alle spalle un triangolo monocromatico e la estendo con il nuovo vertice che aggiungo, studiandone le ulteriori connessioni.
non so se ho capito bene, ma ti ripeto che deve valere per qualsiasi colorazione e ti assicuro che ce ne sono tante.
Qualcosa di vero c'è in quello che dici, ma bisogna ragionare più in astratto, e più in generale.
In attesa che mi venga una idea migliore propongo questa osservazione:
Dati N nodi, il grafo completo, avrà un numero di lati L = N*(N-1) /2
Il numero di triangoli che si formeranno con questi lati sarà T = N*(N-1)(N-2)/3!
Considero ora il rapporto R tra il numero di triangoli T e il numero di lati L.
R = T/L = N*(N-1)(N-2)/3! / N*(N-1) /2 = (N-2)/3
Se N =< 5 R =< 1 Se invece N>5 R>1
Quindi un grafo completo, con al massimo 5 nodi, avrà R minore o uguale 1 , mentre con 6 o più nodi R > 1
Andrebbe dimostrata la seguente affermazione:
Se i triangoli che si creano sono in numero maggiore dei lati che li costituiscono e i lati possono assumere solo 2 colori , avremo almeno un triangolo monocromatico.
Il caso in esame propone N=6. Ci saranno 20 triangoli e 15 lati. il loro rapporto R vale 4/3 > 1
quindi avremo almeno 1 triangolo monocromatico. Ma occorre dimostrarlo.
Scusa Maurizio perché il numero di triangoli sarebbe T = N*(N-1)(N-2)/3! ?
Ogni triangolo è formato da tre elementi scelti nell'insieme di N nodi.
Quindi il loro numero è dato dalle combinazioni. ( n 3) , che andrebbe scritto con latex...
Verificando triangolo e il quadrato sembra che la formula vada bene. (scusa ma come vedi erano le 4 del mattino)
il ragionamento poi sembrerebbe filare, ma non so.. dimostrare che:
Se i triangoli che si creano sono in numero maggiore dei lati che li costituiscono e i lati possono assumere solo 2 colori , avremo almeno un triangolo monocromatico.
bisognerebbe provare. IO ho fatto in altro modo, ma non importa , meglio se troviamo un altra soluzione
un piccolo suggerimento: tenete presente i due articoli che ho scritto prima di questo quiz, soprattutto :
http://www.infinitoteatrodelcosmo.it/2020/03/15/principio-della-colombaia/
questo lo scritto appositamente per il quiz
Intanto proseguo con un approccio alternativo, cercando di generalizzare...
Premessa : un grafo K6 contiene sempre, come sottoinsieme, un grafo K5.
Affinché un grafo K5 non contenga triangoli monocromi è necessario che, in ciascuno dei suoi 5 nodi, i 4 lati che lo collegano agli altri nodi siano 2 coppie di due colori distinti. Per esemplificare , due rossi e due neri.
Possiamo convincerci di questo osservando questi grafi K5 , che rispettano questa regola: se in uno di essi commutiamo il colore di un qualsiasi lato: si viene a formare subito un triangolo monocromo.
Partendo da una configurazione K5 priva di triangoli monocromi, ( ad esempio quella di sinistra, nella figura soprastante) introduciamo i collegamenti con un punto P6.
Se colleghiamo P6 al punto P1 del grafo K5 , con un lato di colore nero, avremo cinque lati che convergono in P1: due lati rossi e tre neri .
Per non generare un triangolo monocromo nero ( P6 P2 P5), non devo collegare ambedue P2 e P5 al punto P6 con lati neri neri. Uno potrà essere nero ma l'altro deve essere rosso. Lo vediamo nella immagine seguente:
Proseguendo nei collegamenti , mi occupo di P3. Per non generare un triangolo monocromo nero P6 P1 P3 , dovrò collegare P3 a P6 con un lato rosso, così:
Resta ora da collegare l'ultimo punto P4. E ciò porta inevitabilmente alla generazione del triangolo monocromo. Infatti, se collego P6 a P4 con un lato nero si forma il triangolo P6 P4 P1 nero, ma se lo collego con un lato rosso, si forma il triangolo P6 P4 P5 rosso.
Un grafo bicolore, estensione di K5 consente , quindi, al massimo 4 collegamenti con un punto P6, senza generare triangoli monocromi. Al quinto collegamento, inevitabilmente, si genera un tale triangolo.
Dato che K6 contiene almeno un triangolo monocromo e qualsiasi grafo completo Kn con n>6 include come sottoinsieme K6, necessariamente anche Kn conterrà almeno un triangolo monocromo
scusa Oreste, la vedo adesso. Non dico niente però...
Nella prima figura del precedente commento di Oreste, i due esempi di grafi K5 proposti sono uno il negativo dell'altro, quindi sostanzialmente sono lo stesso grafo con i colori invertiti. Esistono però altre configurazioni che graficamente hanno un aspetto diverso, come questa...
Ma la diversità , da un punto di vista topologico non esiste, perché vale comunque la medesima regola di avere per ogni punto 2 lati rossi e 2 neri.