Categorie: Fisica classica
Tags: meccanica classica quiz velocità
Scritto da: Vincenzo Zappalà
Commenti:31
QUIZ: avventura a lieto fine su Papalla *
Come tutti sanno, Papalla è un pianeta piuttosto particolare. Esso è completamente ghiacciato e ha un cielo rosa. Anche i suoi abitanti sono rosa e sembrano delle piccole sfere. Si muovono scivolando perfettamente su quel terreno senza attriti. La massa e le dimensioni di Papalla sono esattamente quelle della Terra, per cui ogni cosa pesa esattamente quanto sul nostro pianeta.
Anche su Papalla i bambini sono spesso disobbedienti e corrono in lungo e in largo, anche dove non dovrebbero andare. Gli esseri viventi del pianeta sono tutti pacifici, tranne uno, il terribile mostro di Papalla, il Papallostro arancione. Questa creatura si ciba di tutto ciò che respira e ha una tecnica di cattura molto particolare. Il Papallostro si sistema sul fondo di un buco conico dalle pareti perfettamente lisce e attende che qualche malcapitato cada nella sua trappola. Fortunatamente, è obbligato a stare fermo e i suoi artigli acuminati non possono arrivare oltre una certa altezza: se qualcuno cade nel cono-trappola non può superare l’altezza di salvezza hS,dal vertice del cono. Dopo quel punto non avrebbe più speranza.
Il nostro Papallino, di massa m, si è spinto troppo lontano da casa e, guardando a destra e a sinistra, non si rende conto del buco conico, sempre ben mimetizzato, e vi scivola dentro. La tragedia sembra inevitabile, ma Papallino, come tutti i bambini di Papalla, sa come comportarsi in queste situazioni. Conosce perfettamente l'altezza limite hS che può raggiungere prima di essere catturato.
Scivola un po’ per prepararsi alla manovra e, quando raggiunge il valore di hS, inizia a correre lungo una circonferenza orizzontale (linea tratteggiata rossa). La sua conformazione fisica, che gli permette di muoversi scivolando perfettamente su qualsiasi pendenza, rende attuabile il suo tentativo. Non potrà resistere a lungo, ma emettendo a squarciagola gli ultrasuoni che indicano un pericolo mortale, il padre accorrerà sicuramente in suo aiuto, tirandolo fuori dalla trappola.
E' facile prevedere cosa succederà dopo : su Papalla, le punizioni per i bambini disobbedienti sono molto severe!
Da amici papalliani ho saputo l’esatto valore di hS, che quindi possiamo considerare una grandezza ben conosciuta. Vi chiedo, perciò: “A che velocità Papallino deve correre in tondo, scivolando perfettamente sulla superficie conica, per tenersi sufficientemente lontano dal mostro?”
La soluzione è piuttosto facile, date le conoscenze di meccanica elementare che ormai abbiamo acquisito. Invito, perciò, i più bravi ad aspettare a darmi il risultato. Spero che molti lettori si cimentino in questo facile quiz, senza nessuna paura di sbagliare. La vita di Papallino merita qualche sforzo aggiuntivo…
Posso anche dirvi che esiste un sistema alternativo, estremamente elegante e rapido, per ricavare il risultato. Sono convinto che “qualcuno” cercherà di usarlo (anzi DEVE usarlo), spiegandomi perfettamente, però, le motivazioni per cui PUO’ usarlo… Ovviamente, anche in questo caso, silenzio sul blog, per qualche giorno…
Forza, voglio vedere all’azione molti amici… vi assicuro che è molto facile! E poi… vogliamo o non vogliamo salvare il povero (anche se disobbediente) Papallino?
La figura che segue vi dà tutti i dati necessari per la soluzione del problema, ossia ... solo hS, niente di meno e niente di più…
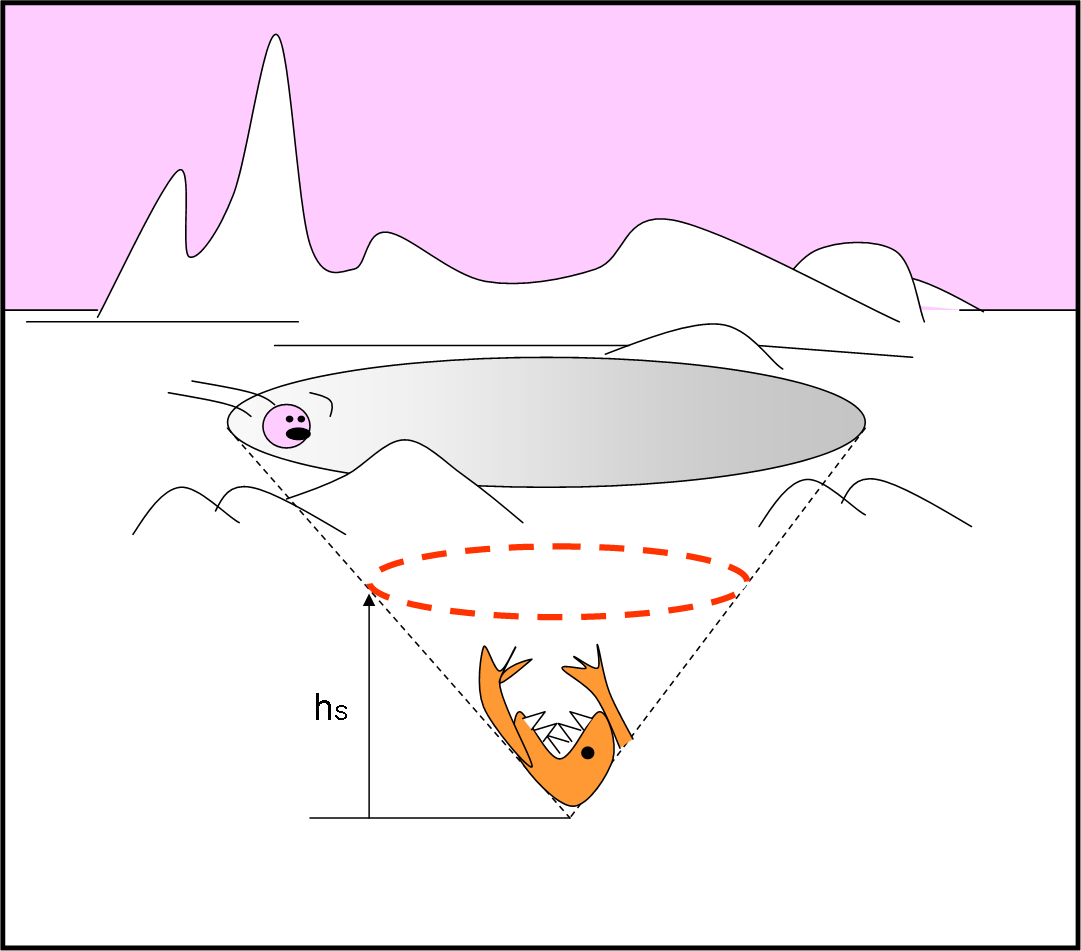
QUI la soluzione (e un approfondimento sul tema introdotto dal quiz)






31 commenti
Scusami Enzo, una precisazione ed una domanda.
PRECISAZIONE:
Il pianeta Papalla dista dalla Terra 100.000 a/l , o almeno questa era la distanza negli anni '60.
Inoltre ricordo che i papallesi erano tutti bianchi, ma questo forse dipendeva dalla TV.
DOMANDA:
Accettando la tua correzione cromatica, ti chiedo se posso assimilare l'arancio del papallostro al rosso. Questo mi faciliterebbe i calcoli della pressione di radiazione esercitata dalla luce riflessa dal papallino (bianca, quindi più energetica) sul papallostro, che riflette sul papallino luce rossa, quindi meno energetica.
La massa non serve...
Solo la velocità può salvare il nostro papallino!!
Essa deve essere superiore a....
No Alvy!
arancione è e arancione deve essere!!!! Se no sarebbe troppo facile...
Oggi, purtroppo, nessuna novità: ad Alba non c'è posto e deve rimanere a Cuneo ancora qualche giorno... Va beh... mi sto preparando per il tour Parigi-Pekino... Per il resto tutto OK.
Beh, l'importante è che si continui lungo la rotta intrapresa (parlo di tua figlia, non della traversata Parigi-Pechino!).
... e visto che il buon Enzo ha voluto riesumare il mitico carosello (quello vero, non la puttanata che la rai ha trasmesso recentemente) , ripropongo il testo (il video lo potete vedere su you tube) del GRINGO, forse il mio preferito; sarebbe riduttivo definirla pubblicità, quei filmini erano piccoli capolavori.
eeeehhh ragazzuoli, allora ero bambino, che ricordi ....
“Laggiù nel Montana tra mandrie e cow-boys/c’è sempre qualcuno di troppo tra noi/
Black Jack va dicendo che troverà il modo/di farmi sembrare un bel colabrodo/
per’ se a provarci un bel dì lo costringo/vedremo chi cola, parola di Gringo
Dal più antipatico dei suoi brutti grugni/m’ha fatto sfidare a un incontro di pugni/
e per ricevuta quel grugno demente/con mezza percossa rispedisco al mittente/
ed ora a noi due sporco fiore del fingo/eh sarebbe ‘del fango’ ma è per far rima con Gringo
In piazza in attesa c’è tutto il villaggio/la Dolly è tremante e le faccio coraggio/
saliamo sul ring ed inizia il gran ballo/ma Black ha per pugno un ferron di cavallo/
così che di un metro all’ingiù mi restringo/ma adesso gli faccio vedere chi è Gringo
Lo invito alla carica lui parte in seconda/mi scanso e le corde facendo da fionda/
ti fanno volare quel grosso salame/a testa all’ingiù in un bidon di catrame/
così che ora sembra un nativo del Chingo/ ehm Congo, mannaggia la rima con Gringo
E adesso siam giunti alla resa dei conti/siam fermi di fronte immobili e pronti/
qualcuno di noi deve fare trasloco/sarà mezzogiorno, mezzogiorno di cuoco/
e vedendo la carne Montana che stringo/alé, vengon tutti a mangiare con Gringo.
Mangiate Montana, è carne ben scelta, così, in gelatina, è pratica, svelta,
il tipo normale o esportazione, in casa, all’aperto, in ogni occasione.
C’è poi Jambonet che puoi fare a fette, comunque le mangi son sempre perfette.
Così nutriente, appetibile, sana, è carne ben scelta, è carne Montana.
Sì... hai ragione... e c'erano fior di registi e di attori... perfino Fellini!
Aspetto la soluzione fatta da altri , dovrei avere più tempo per ragionarci sopra. Posso dire , però , di aver visto veramente il mostro Papallostro intanato o meglio insabbiato sotto l'apice di un cono di sabbia (esattamente come Papallostro nella figura ). D'estate, il pavimento ( in terra battuta) del portico posto a ridosso del mio bellissimo fienile presenta numerosi piccoli coni . Basta avere pazienza , guardare attentamente e appena una incauta formica si avventura lungo la sponda del cono , la si vede inesorabilmente scivolare fino al fondo dove con uno scatto felino escono due uncini ricurvi che azzannano e fanno sparire in un nanosecondo la malcapitata ( papallina ) . Papallostro non è altro cha la " formicaleone " ; certo che ne ha di fantasia la natura !
Grande Claudio! Hai proprio ragione...
Beh... signori! nessuna risposta?
I più bravi stanno zitti... gli altri tentennano e la nostra papallina prima o poi cade! Abbiate pietà di lei, sta aspettando cosa deve fare
Guardate che è proprio semplice... moto circolare uniforme e un paio di forze da contrapporre, senza nemmeno scomodare l'energia... Da "qualcuno" aspetto sempre la "parola" magica (mi basta quello...)
Ho trovato la risposta! E' il raggio di Alzheimer!
Ah no! Quello è il dottore tedesco che mi nasconde le cose...
Va beh, allora mi espongo ... però non voglio responsabilità eh?!?!
SOLUZIONE BRUTTA, SPORCA e CATTIVA (cioè dinamica)!
Ragioniamo sul piano considerando la sezione del cono intercettata da un piano verticale passante per l'asse del cono stesso.
Chiamiamo α il semiangolo al vertice del cono. La pallina si muove di moto circolare uniforme alla quota hs, come da figura.
Sulla pallina agiscono due forze: la forza peso, diretta verso il basso e la forza centrifuga (la pallina NON è infatti un riferimento inerziale) diretta orizzontalmente verso l'esterno del cono.
Imponiamo la condizione di equilibrio tra le due forze, ovvero tra le due componenti parallele alla parete obliqua del cono. Queste due componenti, orientate in modo opposto, varranno:
Fg = m*g*cosα
Fc = m*v^2*sinα/r
in cui:
g è l'accelerazione di gravità nel punto occupato dalla pallina;
r è la distanza della pallina dall'asse del cono.
v è la velocità periferica della pallina.
Si ottiene:
m*g*cosα = m*v^2*sinα/r , da cui:
v = (g*r*cotgα)^0,5
Osservando che: r=hs*tgα , ovvero hs=r*cotgα si può scrivere:
v = (g*hs)^0,5.
SOLUZIONE BELLA, LINDA ed AULICA (cioè energetica)!
Poniamo la condizione di equilibrio, sempre nel caso del moto circolare uniforme, tra forza centrifuga e forza centripeta di tipo gravitazionale.
Fc = m*v^2/r
Fg = G*M*m/r^2
Dall'equzione di uguaglianza si ottiene:
m*v^2 = G*M*m/r
Al primo membro ho il doppio dell'energia cinetica, al secondo l'energia potenziale.
REGOLA GENERALE (sempre e solo nel caso di moto circolare uniforme):
Data una circonferenza, si ha che Ep = 2*Ec.
Se si passa da una circonferenza ad un'altra di diverso raggio, la relazione viene mantenuta: ΔEp = Δ(2*Ec).
Ora, nel nostro caso, immaginiamo di calcolare la variazione di energia potenziale che si ha passando dal vetice del cono all'altezza hs: ΔEp = m*g*hs.
La variazione di energia cinetica corrispondente sarà: ΔEc = 0,5*ΔEp , ovvero:
0,5*m*v^2 = 0,5*m*g*hs, da cui, ancora una volta:
v = (g*hs)^0,5.
La condizione restrittiva cui accenna Enzo consiste nel fatto che, nel calcolo di ΔEp, ho indebitamente considerato costante l'accelerazione di gravità g nel passare da una quota ad un'altra; sappiamo infatti che g dipende dall'inverso del quadrato della distanza dal centro di gravità.
Se però la differenza di quota è trascurabile rispetto al raggio della Terra, questa approssimazione è permessa.
COMPLICAZIONE
Che succede se, a seguito di un non meglio identificato sommovimento, l'angolo al vertice del cono cambia? Perchè, caro Enzo, non proponi un approfondimento del quiz in tal senso?
caro Alvy,
nella soluzione energetica non vedo h... (roba da poco).
La velocità dipende solo da h e g, per cui anche la tua complicazione sembra facilmente risolta...(se g è ammessa costante, ma lo è).
Da te, però, mi aspettavo un "nome" che avrebbe risolto subito il problema con una sola formula. Ci sei girato intono (lo ammetto), ma volevo vederlo scritto insieme al perché si può usare...
Scusa Enzo, non capisco a quale h ti riferisci nella soluzione energetica.
hs c'è, ma sicuramente si tratta di altro.
Sull'altra questione, beh forse ti riferisci al principio di conservazione dell'energia.
caro Alvy,
Dovresti, poi, spiegare meglio come ottieni l'uguaglianza tra forza centripeta gravitazionale e forza centrifuga... Questo è vero solo se la pallina ruota attorno alla massa M. In tal caso h perde di senso...
Tu forse hai cercato di descrivere in modo generale proprio quello che io mi aspettavo... Ma la spiegazione del perché lo puoi estrapolare al cono mi sembra insufficiente...
ma può darsi che sia io a non capire il tuo procedimento logico. Puoi spiegarti meglio?
Allora.
Ho considerato il caso del moto circolare uniforme di un oggetto m ruotante intorno ad un oggetto M che lo attrae gravitazionalmente. In questo caso va da sé che deve esserci equilibrio tra la forza centrifuga e la forza centripeta gravitazionale. Dall’equazione di equilibrio si vede, con un semplice passaggio matematico, che: Ep = 2*Ec, dove Ep è l’energia potenziale del sistema ed Ec è l’energia cinetica dell’oggetto m, visto che M è considerato fermo.
Di qui discende la regola, evidentemente generale (sempre in riferimento ai moti circolari uniformi) che l’energia totale posseduta dal sistema è pari a:
Ep = - G*M*m/r
Ec = 0,5*m*v^2
Et = Ep + Ec = - 2*Ec + Ec = - Ec.
Questa regola, come detto, ha validità generale. Ora, se varia il raggio dell’orbita circolare, la regola non viene meno, nel senso che alla variazione dell’energia potenziale corrisponde anche una variazione dell’energia cinetica secondo il rapporto già individuato.
Se ora, nel nostro caso, io considero una variazione del raggio dell’orbita portando l‘oggetto rotante dal vertice del cono fino alla posizione finale all’altezza hs, posso valutare la variazione dell’energia potenziale come: Ep = m*g*hs.
A questa variazione di Ep corrisponde la variazione di Ec, nella misura di: ΔEc = 0.5 *ΔEp = 0,5*m*g*hs.
In definitiva: v^2 = g*hs.
Temo di non riuscire a spiegarmi meglio di così. Può bastare?
Sai, non vorrei essere off-topic, nè flame, nè ... vattelapesca!
Ops, dimenticavo ... l'estrapolazione al cono.
In effetti mi limito ad applicare al moto circolare uniforme le regole generali che valgono per quel tipo di moto.
Mi sembra che la presenza del cono non abbia molta importanza, o mi sbaglio?
Non è che stai cercando di confondermi le idee?

No Alvy,
ho avuto conferma dell'approccio che stavi usando, ma di cui non ero sicuro perché il passaggio da moto circolare a cono era un po' aleatoria. In altre parole, e non giriamoci più attorno, hai enunciato il teorema del viriale! Quello che mi aspettavo da te, dato che l'hai già proposto varie volte. La situazione (particella in moto, soggetta a energia cinetica e energia potenziale) è tale da poterlo applicare e quindi basta dire che Ec=1/2 Ep e questa formula dà il valore di v, qualsiasi sia l'apertura del cono, senza bisogno di passare dalle forze...
Comunque, complimenti! sei molto ferrato in meccanica e non solo. Non è che sei un fisico in incognito che cerchi di mettermi alla prova???????
Si Enzo, effettivamente il mio vero nome è Werner Heisenberg ed ho un pò giocato con te!
Senti Enzo, ho solo messo in pratica qualche formuletta di fisica elementare studiata, a suo tempo, tra liceo ed università. Il mio solo merito, davvero poca cosa, è di aver mantenuto un minimo di "destrezza" avendo continuato a coltivare la mia passione per la fisica e l'astronomia.
A proposito: anche se mi sarebbe molto piaciuto frequentare il corso di laurea in fisica, ho dirottato su ingegneria (scelta di compromesso a fini lavorativi. Ho sbagliato? chissà ...) .
Riguardo al teorema del viriale, ho un sacro terrore a nominarlo, giacchè ogni volta sono bacchettate da orbi.
Sono comunque contento di non aver scritto fesserie e di non esere off-topic ...
Ciao Enzo, ero arrivato alla soluzione dinamica (abbastanza semplice) Fc=Fg. In genere mi incaglio sempre quando si inizia a parlare di angoli, per esempio mi sono perso per trovare r, quando poi era una banalità assurda (devo anche dire che non ho avuto molto tempo per pensarci, ma mi sarebbe dovuto venire in mente all'istante). Purtroppo non avendo fatto trigonometria alle scuole non mi viene molto naturale
Allora Enzone, scusami ma sono curioso di vedere cosa succede se varia α (semiangolo al vertice del ... triangolo).
Sfruttando il momento angolare P (così applichiamo … tutto) , abbiamo che quest’ultimo si mantiene costante al variare dell’apertura del cono.
P = m*v*r
in cui r è la distanza di m dall’asse di rotazione.
Abbiamo stabilito che:
v = (g*hs)^0,5
r = hs*tg α.
da cui: P = m*[(g*hs)^0,5]*hs*tg α.
Uguagliamo ora i momenti angolari di due generiche situazioni :
[(g*hs)^0,5]*hs*tg α = [(g*hs’)^0,5]*hs’*tg α’
In conclusione:
(hs/hs’)^3/2 = tg α’/tg α
OK?
scusa Alvy,
ma non ti seguo... cosa vorresti trovare? La relazione tra hs e gli angoli è cosa puramente geometrica e non fisica. E' inutile introdurre relazioni fisiche, dato che vi sono solo rapporti tra lunghezze e angoli... Il punto -mi sembrava- era di capire cosa succedeva alla pallina se si apriva il cono e non di avere una relazione tra hs e l'angolo di apertura. Il fatto stesso che la velocità della pallina dipende solo da hs, è sufficiente a dire che è indipendente dall'apertura del cono, ossia dall'angolo alfa...
O volevi trovare un'altra cosa?
Mi sono limitato ad applicare il principio di conservazione del momento angolare.
L'assunto, sempre che sia corretto, è che variando l'apertura del cono rimanga immutato il momento angolare della pallina (sempre, ovviamente, al netto delle inevitabili dissipazioni di energia che, d'altra parte, non consideriamo mai nei nostri esperimenti ideali).
La relazione (hs/hs’)^3/2 = tg α’/tg α indica come varia la quota raggiunta dalla pallina al variare dell'apertura del cono, partendo dal presupposto che si conservi il momento angolare.
Non è corretto?
Cavolo Enzo, hai ragione, ho ottenuto una relazione puramente geometrica.
Però sono partito da un principio fisico (la conservazione del momento angolare!).
Davvero curioso?!
Come si spiega Enzo?
caro Alvy,
stiamo dicendo due cose diverse...
io intendevo dire che se allargo il cono, ma mantengo sempre la stessa altezza hS, la velocità rimane la stessa. Il problema era questo e l'apertura del cono è ininfluente per il risultato. hS era un dato fisso di partenza e l'apertura del cono non comporta nessuna variazione nel risultato finale. Tu, invece, ammetti che hS possa cambiare, ma allora il problema è un altro...E' ovvio che in quel caso cambia la velocità della pallina, ma noi volevamo trovare la velocità per una certa hS. Tuttavia, bastava rifare il calcolo cambiando hS e si trovava la nuova v, funzione della sola hS.
Sulla conservazione del momento angolare... attenzione. Se il moto avviene nel piano orbitale, allargare o diminuire il raggio implica una variazione di forza centripeta e centrifuga che passa per il centro, e quindi ha momento nullo (pattinatrice su ghiaccio). Nel caso particolare, il momento della forza di gravità non è nullo e varia in funzione della distanza...
Scusa se ti scrivo a rate, è che ho la caffettiera sul fuoco!
Allora Enzo, il fatto che, partendo da un principio fisico sia approdato ad una ovvia relazione geometrica SEMPRE vera, dovrebbe dimostrare che l'assunto (conservazione del momento angolare) è NECESSARIAMENTE vero.
E' chiaro che la mia elucubrazione non ha risolto alcun mistero dell'universo; è comunque stata un utile esercizio, almeno per me.
Devo sapere altro Enzone? Mi sfugge qualcosa?
Adesso, in attesa di gustare la tua risposta, mi gusto il mio caffè!
riporto la tua "complicazione":
"Che succede se, a seguito di un non meglio identificato sommovimento, l’angolo al vertice del cono cambia? Perchè, caro Enzo, non proponi un approfondimento del quiz in tal senso?"
La risposta è che se cambia l'angolo non cambia niente, dato che la velocità è indipendente dall'angolo... Lo stesso risultato si ottiene per qualsiasi apertura del cono, a parità di hS.
OK. Grazie
ma, forse, intendiamo due cose diverse... e abbiamo ragione tutti e due...
Penso di aver capito...
Tu imponi la conservazione del momento angolare e lasci libera la pallina di muoversi in su è in giù. Allora le cose funzionano, ma è un problema diverso da quello impostato. Per conservare il momento deve cambiare la velocità e quindi anche hS... Ti torna?
OK Alvy,
per farti contento scrivo un articoletto sul teorema del Viriale, che ha come ricaduta la legge di Keplero nel caso che avevi proposto tu... In realtà, riprendo quanto avevo scritto nel libro "Il gioco delle stelle"...
Non so se riesco oggi, dato che ci hanno chiesto di stare accanto a Barbara oltre ai tempi di visita per aiutarla a stare seduta e magari a muoverla (forse non oggi, ma nei prossimi giorni). Meno sta sdraiata e meno problemi polmonari possono insorgere... In tal caso, mi resteranno solo le ore pre-mattutine per il blog. Se tutto va bene la faccenda dovrebbe durare un mesetto (ci sarà anche l'alimentazione da seguire attentamente). Seguirà una valutazione psicofisica e si deciderà se ha bisogno di riabilitazione presso un istituto o se basterà portarla a casa. Teniamo anche conto che per almeno tre mesi non possono rimettergli il pezzo d'osso e bisogna stare bene attenti che non prenda colpi alla testa... Insomma, un periodo di grande tensione e responsabilità. Da un lato il morale è salito, dall'altro le incombenze pratiche si sono appesantite. Ma ne sono ben contento!!! E voi avrete sicuramente pazienza...
Si Enzone, ora ci siamo.
In quanto all'articolo sul teorema del .... posso dirlo? ... del ..... viriale, beh, amico mio, lo attendo con (vera) ansia!
Vai grande Enzone!
Per il resto, come hai giustamente detto, benvengano queste incombenze pratiche.
Salutoni a Barbara, anche se non mi conosce ... per sua fortuna!
Senti Enzo, mi devi scusare, ma a volte parto per la tangente con i miei pensieri dando per scontate cose che non lo sono!
In questo caso ho cambiato le regole del gioco rispetto alla tua impostazione del problema e, seguendo il mio ragionamento, ho ritenuto che tu mi seguissi senza difficoltà.
Abbi pazienza; è che, come si dice dalle mie parti, "me devo dà 'na carmata!"
P.S.: No, non sono di Bergamo Alta.
Figurati Alvy...
oltretutto cade a fagiolo con il viriale...