Categorie: Meccanica quantistica
Tags: disuguaglianza di Bell ket legge di Malus notazione di Dirac polarizzazione fotoni vettori
Scritto da: Fabrizio
Commenti:9
Disuguaglianza di Bell parte 2 - Alcuni fatti sperimentali
Questo articolo è stato inserito nella pagina d'archivio dedicata alla Disuguaglianza di Bell
LA DISUGUAGLIANZA DI BELL
Alcuni fatti sperimentali
Parto ricapitolando i punti principali dell'articolo precedente.
|
I fotoni che transitano in un cristallo polarizzante assumono particolari proprietà di polarizzazione e posizione. I fotoni vengono rivelati da contatori posti su due diverse traiettorie. I fotoni rivelati dal medesimo contatore hanno la stessa direzione di polarizzazione. La direzione di polarizzazione dei fotoni rivelati da un contatore è perpendicolare a quella dei fotoni rivelati sull'altro contatore. Le direzioni di polarizzazione dei fotoni rivelati dipendono dall’orientamento del cristallo, ma non dipendono dalla direzione di polarizzazione dei fotoni entranti. Il numero di fotoni rivelati in uscita è, idealmente, uguale a quello dei fotoni entranti. |
Per arrivare a valutare l’effetto della disuguaglianza di Bell occorre sapere quale è la frazione di fotoni rivelati in ciascuno dei due contatori quando i fotoni in ingresso sono polarizzati in una direzione definita.
L’unico modo per saperlo è tramite esperimenti. Si fa uso di strumenti di misura in grado di rivelare e contare, direttamente o indirettamente, i fotoni. Due di questi strumenti sono posti in corrispondenza delle due traiettorie dove appaiono sullo schermo i fotoni transitati nel cristallo.
Noi possiamo immaginare di utilizzare una configurazione di prova come quella schematizzata nella figura. Le configurazioni di prova che descrivo sono molto idealizzate. Le riporto perché spero servano a visualizzare e capire meglio il fenomeno che è al centro della disuguaglianza di Bell.

Figura 2.1
La configurazione è simile a quella del precedente articolo. La differenza è nella sorgente che produce fotoni tutti polarizzati in una certa direzione.
Potrebbe essere l’uscita di un altro polarizzatore. Possiamo immaginare di cambiare la direzione di polarizzazione dei fotoni prodotti ruotando questa sorgente.
La sorgente invia i fotoni prodotti verso un cristallo polarizzante. Sappiamo che i fotoni passati nel cristallo saranno rivelati da uno dei due contatori. I fotoni rivelati dai due contatori hanno polarizzazione perpendicolare tra loro. Nella figura i fotoni rivelati dal contatore A sono polarizzati verticalmente e, di conseguenza, i fotoni rivelati dal contatore B sono polarizzati orizzontalmente.
Uso i termini verticale ed orizzontale solo per identificare delle direzioni nella figura. Questi termini non hanno alcun riferimento alla direzione del campo gravitazionale che non ha effetti sensibili su quanto sto dicendo.
La prova consiste nel variare la direzione di polarizzazione dei fotoni entranti e verificare come cambia il numero di fotoni rilevati dai due contatori.
Quello che ci interessa sono gli angoli tra la direzione di polarizzazione dei fotoni entranti e quelli rivelati nei contatori.
Chiamiamo γ l’angolo tra la direzione di polarizzazione dei fotoni entranti e quello dei fotoni nel contatore A e chiamiamo δ l’angolo tra la direzione di polarizzazione dei fotoni entranti e quello dei fotoni nel contatore B. Ricordiamo che la polarizzazione rivelata dai contatori è determinata dal posizionamento del polarizzatore.

Figura 2.2
Questi due angoli sono in relazione tra loro γ=δ-90°.
Ciò che otterremmo ruotando la sorgente, almeno idealmente, è quello che vediamo nella figura.
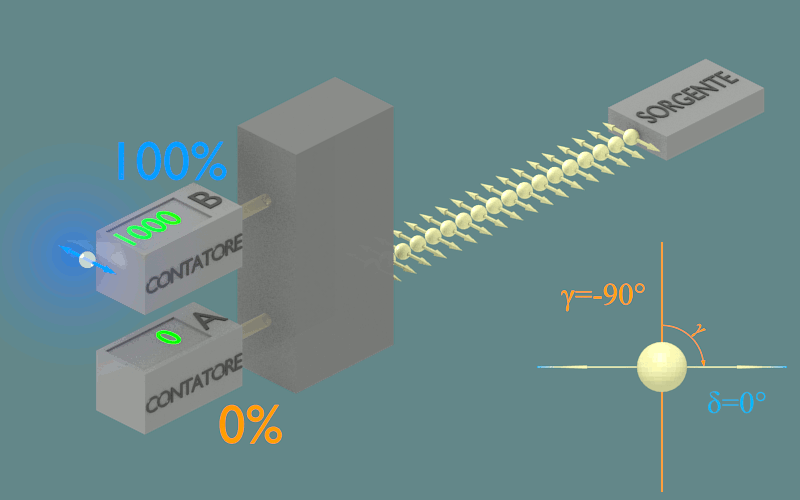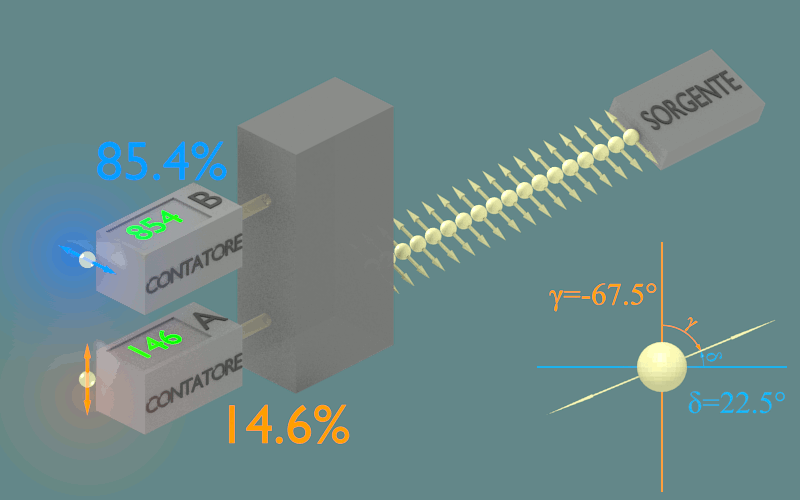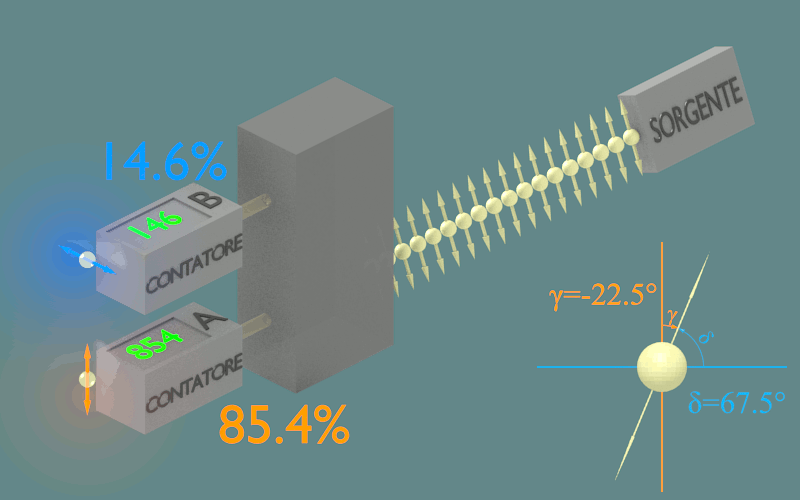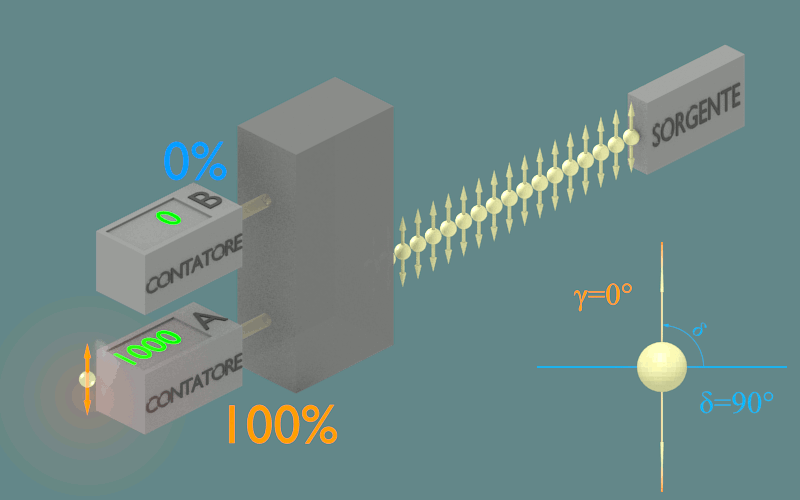
Figura 2.3
Solo se la direzione di polarizzazione dei fotoni entranti è uguale ad una delle due possibili indicate dai contatori, δ=0° o γ=0°, allora tutti i fotoni mantengono la loro direzione di polarizzazione e vengono tutti rivelati dal contatore corrispondente. Solo in questi due casi abbiamo la certezza del risultato della misura.
Quando la direzione di polarizzazione dei fotoni entranti e diversa da quella dei fotoni uscenti (δ≠0° e γ≠0°) allora i fotoni saranno rivelati su entrambi i contatori. Ciascun fotone è comunque rivelato da un solo contatore, l'uno o l'altro in modo casuale.
La frazione di fotoni che sarà rivelata da ciascuno dei due contatori è data da un grafico come questo.
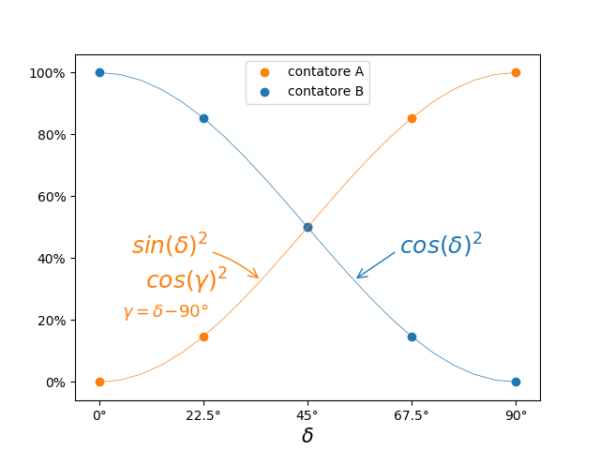
Figura 2.4
I risultati ottenuti si posizionano su due curve che seguono ciascuna una nota funzione trigonometrica: cos(δ)² e cos(γ)².
Questa legge è nota come legge di Malus.
Notate che cos(γ)²= cos(δ-90°)²=sin(δ)² per la relazione che lega seno e coseno di angoli che differiscono di 90°. Relazione che abbiamo visto nell'appendice del precedente articolo.
Ci sono alcune caratteristiche di queste funzioni che torneranno utili in seguito. Le elenco qui sotto:
|
Negli esperimenti ideali visti sopra abbiamo immaginato di variare la polarizzazione dei fotoni entranti con la rotazione della sorgente. Ci possiamo domandare che cosa accadrebbe se invece lasciassimo invariata la polarizzazione dei fotoni entranti e ruotassimo il cristallo polarizzatore.
Il risultato sarebbe lo stesso poiché dipende solo dal valore assoluto dell’angolo tra polarizzazione del fotone entrante e la direzione di polarizzazione dei fotoni rivelati.
Ruotare la sorgente o ruotare il cristallo fa cambiare quest’ultimo angolo ed il risultato cambia nello stesso modo. In effetti non dipende neanche dal senso di rotazione, poiché ciò che interessa è il valore assoluto dell'angolo. Le due configurazioni nella figura sotto sono equivalenti. In effetti sarebbe molto strano se fosse il contrario. Significherebbe che lo spazio non è isotropo, cioè il risultato dell'esperimento dipende da come siamo orientati nell'universo. O, più probabilmente, che qualcosa che non abbiamo considerato interferisce con il nostro esperimento.

Figura 2.5
A questo punto abbiamo accumulato una serie di fatti. Dal prossimo articolo inizieremo a vedere come spiegano questi fatti le due teorie che vogliamo mettere a confronto. Inizieremo con la teoria standard e poi vedremo come gli stessi fatti potrebbero essere spiegati con una teoria locale, che non prevede azioni a distanza istantanee.
Nella teoria standard della MQ hanno un ruolo fondamentale i vettori. Conviene iniziare qui a prendere confidenza con queste entità matematiche. Vi propongo qui di seguito una scheda introduttiva ai vettori, almeno ai vettori nella loro forma più semplice. Sarà sufficiente per gli scopi di questa serie di articoli.
|
La prima immagine che viene normalmente associata alla parola vettore è qualcosa di questo tipo.
Figura 2A.1 Uno spostamento nello spazio che possiamo rappresentare con una freccia. Si tratta quindi di un oggetto geometrico con una direzione, un verso ed una lunghezza che può essere considerato il prototipo del vettore. ...
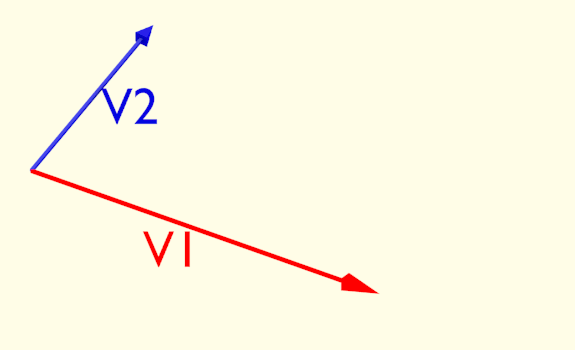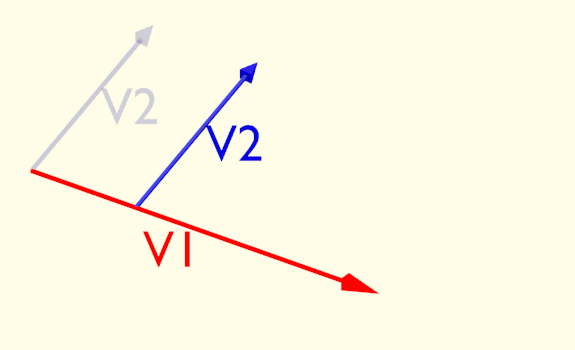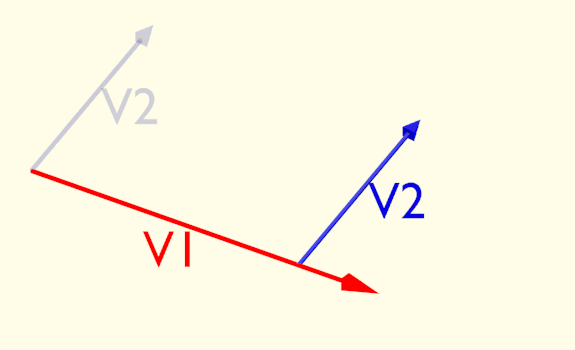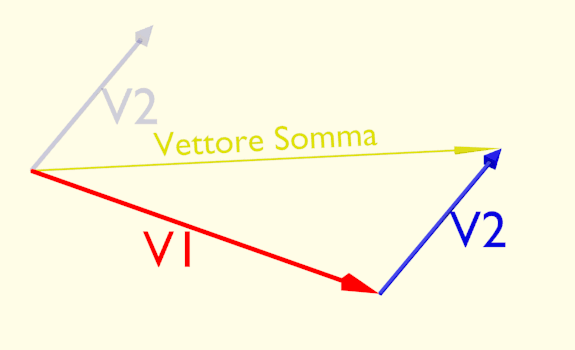
Sui vettori e con i vettori possono essere fatte delle operazioni. La prima è la somma di due vettori. Il risultato di questa operazione è un altro vettore. Quando pensiamo ad un vettore come uno spostamento nello spazio, la somma viene naturale. Dalla fine di un vettore spostamento proseguo con l’altro spostamento ed ottengo il punto di arrivo delle spostamento totale. Il vettore che unisce il punto di partenza con quello di arrivo è il vettore somma.
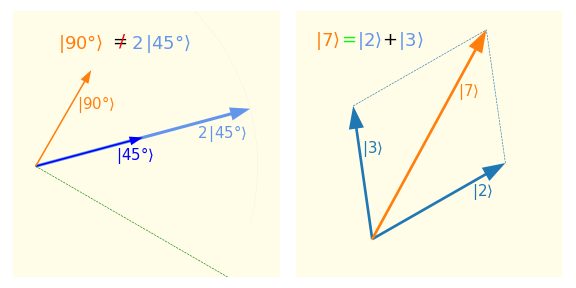
Figura 2A.2 Vediamo l'operazione di somma di vettori come può essere espressa nella notazione di Dirac.
Figura 2A.3 La seconda operazione è il prodotto di un numero con un vettore che produce un altro vettore. Nel caso del vettore freccia che abbiamo visto nelle figure sopra, il risultato sarà un vettore con la lunghezza ottenuta moltiplicando la lunghezza originaria per il numero, la direzione sarà la stessa ed il verso sarà determinato dal segno del numero. Vediamo un paio di esempi.
Figura 2A.4 In questo modo è possibile “mescolare numeri e vettori”. Vederemo più avanti che ci sarà molto utile.
A noi basterà utilizzare solo numeri reali in queste operazioni.
Il risultato delle due operazioni che abbiamo visto sono vettori. A loro volta, questi vettori risultanti possono entrare a far parte di altre operazioni. Le regole che seguono queste operazioni sono sostanzialmente uguali a quelle dell'algebra elementare che abbiamo studiato a scuola. Vediamo alcuni esempi.
Figura 2A.6 Un suggerimento preso da un noto libro di MQ: “C'è un buon modo per ricordare tutte queste regole: fate come vi viene naturale.”. Aggiungerei con qualche attenzione come abbiamo visto nei due casi di figura 2A.5. Le operazioni di prodotto tra numero e vettore e l’operazione di somma aprono la possibilità di rappresentare i vettori utilizzando altri vettori. Il termine normalmente utilizzato è quello di combinazione lineare di vettori. Questo ci permette di lavorare più agevolmente con i vettori. Cerco di spiegarmi.
Figura 2A.7 Qualsiasi operazione faccio, il risultato alla fine può essere espresso come combinazione lineare degli stessi vettori. Questo mi sembra un vantaggio evidente. Certo, il vantaggio si ha se utilizziamo uno stesso insieme di vettori per rappresentare tutti gli altri. Ma quanti vettori servono per poter rappresentare tutti gli altri vettori? Dipende dal problema che stiamo affrontando. Nel nostro spazio fisico normalmente ne servono 3. Per questo diciamo che viviamo in uno spazio tridimensionale. Se ci limitiamo a vettori che giacciono su uno stesso piano ne bastano 2. Per questo diciamo che il piano è bidimensionale. Per trattare la polarizzazione dei fotoni ci basterà uno spazio bidimensionale.
Un insieme di vettori con i quali possiamo rappresentare tutti gli altri vettori del nostro problema è detta base, nome che mi sembra già significativo per indicarne l’importanza. Nella prossima tabella introduco la terminologia normalmente utilizzata.
Figura 2A.8 Normalmente ci sono infinite basi tra le quali scegliere quella con la quale scomporre i nostri vettori. La scelta è fatta tenendo conto di eventuali semplificazioni che si possono ottenere e considerando il significato fisico che può avere una particolare base. Può anche accadere che nel corso del processo di risoluzione si cambi la base con la quale si opera. Non è obbligatorio, ma ci sono numerosi vantaggi se una base è formata da vettori ortogonali. Ed altri vantaggi se i vettori base, oltre ad essere ortogonali tra loro, sono anche di lunghezza unitaria. Queste basi costituite da vettori unitari e perpendicolari tra loro vengono chiamate ortonormali. Noi utilizzeremo basi sempre ortogonali e spesso unitarie, come normalmente avviene in MQ, dove questo tipo di basi hanno un importante significato fisico. La espansione di un vettore unitario in una base ortonormale ha una espressione particolare come appare nella figura seguente.
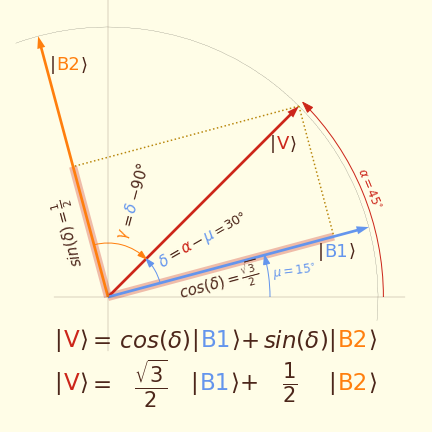
Figura 2A.9 Conviene ricordare l'espressione evidenziata in fondo alla figura facendo attenzione a come sono collocati nella figura gli elementi che la compongono. In varie forme, ritornerà spesso nei prossimi articoli. Notate che le componenti, cos(δ) e sin(δ), corrispondono alla lunghezza delle proiezioni ortogonali del vettore sulle basi. Qui sotto un esempio di elaborazione della figura sopra con qualche dato numerico.
Figura 2A.10
|
Per ora è tutto, arrivederci alla prossima.
Fabrizio Panaioli 2020













9 commenti
crediamo che l'universo stia subendo una espansione accelerata.
sappiamo però che il vuoto non può essere vuoto per il principio di indeterminazione e di conseguenza man mano che si crea nuovo vuoto si deve creare anche nuova massa/energia.
ma se questa massa/energia che prima non c'era si crea dal nulla questo viola il principio che l'energia totale di un sistema deve rimanere costante
come si spiega?
Ciao Michele, ti riferisci alla teoria dell'universo stazionario di Hoyle, Gold, Bondi (1946) ?
Credo che quel modello cosmologico non sia confermato dai dati osservativi e oggi non sia ritenuto valido.
Michele,
la domanda che fai va molto oltre l'argomento trattato nell'articolo dove ho appena accennato ad alcuni aspetti della meccanica quantistica non relativistica. Per rispondere compiutamente alla tua domanda occorrerebbe rivolgersi alla teoria quantistica dei campi. La teoria che tratta anche la creazione e la annichilazione delle particelle. Servirebbe anche invocare qualche teoria cosmologica che inquadri l'espansione dell'universo più o meno accelerata. La mia risposta onesta sarebbe quindi: non lo so. Forse una risposta semplicistica può rimandare allo stessa indeterminazione che citi come causa della creazione di materia/energia. Localmente per un tempo sufficientemente breve l'energia non necessariamente si conserva.
C'è anche da dire che il fenomeno della espansione dell'universo e quello della creazione e annichilazione di particelle nel vuoto possono avere una relazione. Purtroppo sembra che le teorie ed i dati sperimentali dei due fenomeni non vadano molto d'accordo. Sembra ci sia una 'modesta' divergenza di circa 120 ordini di grandezza.
innanzitutto grazie.
questa è una questione che mi incuriosisce parecchio, ma più cerco meno trovo risposta.
peraltro mi sembra ancora più assurdo perchè la creazione di nuova massa/energia dovrebbe rallentare l'espansione dell'universo mentre i dati sperimentali suggeriscono che sia in espansione accelerata, tant'è che è stata introdotta una energia oscura di segno opposto per spiegarla
sarei curioso di sapere se qualcuno ha mai provato a calcolare la posizione delle galassie 11 miliardi di anni fa per vedere quale poteva essere la loro posizione e se la cosa poteva aver senso.
mi spiego, se calcolando a ritroso si ottenessero ad esempio galassie una sopra all'altra o troppo lontane per essere emerse dal periodo caldo nei tempi giusti evidentemente c'è un problema nei dati/formule che abbiamo oggi.
Michele,
la tua domanda ha sollecitato anche la mia curiosità. Ho cercato di recuperare e mettere ordine nel poco che so sulla materia.
Te lo propongo sperando di darti qualche informazione utile anche se approssimata.
In qualche modo si può ricavare dalla famosa equazione di Einstein (in realtà anche da quella di Newton per quanto riguarda la massa) che il tasso di espansione dipende dalla densità di energia dell'universo. (Nota che nei modelli cosmologici si suppone l'universo omogeneo, quindi in ogni istante la densità d'energia varia nel tempo mantenendosi uguale in ogni punto dello spazio.)
C'è una differenza importante tra la densità dell'energia/materia oridinaria e quella del "vuoto"
La densità dell'energia/materia oridinaria si riduce con l'espansione perchè l'energia/materia si diluisce con l'aumento di volume (in modo leggermente diverso tra materia e radiazione), invece la densità di energia del 'vuoto' rimane costante perchè è proprio associata al volume.
Quindi il contributo che materia/energia ordinaria danno al tasso di espansione decresce con l'espansione, quindi l'espansione tenderebbe a rallentare. Il contributo dell'energia del vuoto rimane costante con l'espansione. Cioè c'è un contributo costante al tasso di espansione. Se il tasso di espansione è costante significa che l'espansione cresce esponenzialmente. Se il tasso di interesse è costante e reinvesto gli interessi, il valore degli interessi cresce ogni anno. Magari inizialmente è poco perchè il capitale è piccolo, ma sommando al capitale gli interessi, di anno in anno diventa sempre più grande.
Per spazi curvi le cose si complicano un poco, ma la sostanza credo rimanga invariata.
no, aspetta, non mi è chiaro quello che stai dicendo.
in che senso "il contributo che materia/energia ordinaria danno al tasso di espansione decresce con l'espansione"?
stai dicendo che il tasso di espansione aumenta all'aumentare della densità di materia/energia?
cioè, la materia ordinaria attrae e di conseguenza dovrebbe (secondo me) rallentare l'espansione. E man mano che la densità diminuisce questo freno dovrebbe diminuire a sua volta, di fatto aumentando la velocità di espansione.
Caro Michele,
tu dici: "sappiamo però che il vuoto non può essere vuoto per il principio di indeterminazione e di conseguenza man mano che si crea nuovo vuoto si deve creare anche nuova massa/energia.
ma se questa massa/energia che prima non c'era si crea dal nulla questo viola il principio che l'energia totale di un sistema deve rimanere costante".
In parte è vero, ma non completamente.. Vi sarebbe infatti una continua nascita e morte di particelle e antiparticelle che creerebbero energia senza aggiungere alcuna massa. Molti fenomeni sembrano dimostrarlo, come l'effetto Casimir e la stessa produzione di raggi gamma. Capire come tutto ciò avvenga e su che scala è ancora un mistero (non per niente si ipotizza un'energia oscura). Andare a fondo vorrebbe dire risolvere il problema che, come dice Fabrizio, è ancora ben lontano dalla nostra comprensione. Direi, quindi, di accontentarci della conferma dell'esistenza di effetti non locali. Oltre ciò non è materia per un blog divulgativo...
Devo dare ragione a Enzo. Non è un argomento adatto ad essere trattato, specialmento limiatandosi allo spazio di un commento. Provo comunque a non lasciare appeso l'ultimo punto sollevato da Michele. Spero che Enzo mi perdoni.
Probabilmente ho usato nella mia risposta dei termini non completamente adatti a descrivere il caso, almeno se lo si interpreta in termini Newtoniani.
Il tasso di espansione decresce con il decrescere della densità di materia. Intendo dire che nella espressione del tasso di espansione c'è un termine che dipende dalla densità di materia.
Un esempio molto vicino a quello dell'espansione, almeno in termini Newtoniani, è il lancio di un missile da un pianeta su una traiettoria radiale. Per semplicità lo lanciamo alla velocità di fuga. L'energia cinetica è uguale alla energia potenziale: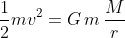 . Riorganizando l'espressione, dividendo per r quadro e accorpando le costanti ottengo che
. Riorganizando l'espressione, dividendo per r quadro e accorpando le costanti ottengo che ^2=K\frac{M}{r^3}{\color{Blue}&space;}}) . A sinistra c'è il quadrato del tasso di crescita della distanza del missile. A destra, oltre alla costante, c'è una espressione che è proporzionale alla densità media di materia nel volume attorno al pianeta sottostante il missile. In questo caso un modo strano per interpretare questo termine, ma comunque corretto. Questo termine diminuisce più il missile si allontana e cosi fa il tasso di crescita della distanza. E' questa la relazione tra tasso di crescita e densità alla quale mi riferivo.
. A sinistra c'è il quadrato del tasso di crescita della distanza del missile. A destra, oltre alla costante, c'è una espressione che è proporzionale alla densità media di materia nel volume attorno al pianeta sottostante il missile. In questo caso un modo strano per interpretare questo termine, ma comunque corretto. Questo termine diminuisce più il missile si allontana e cosi fa il tasso di crescita della distanza. E' questa la relazione tra tasso di crescita e densità alla quale mi riferivo.
Cosa c'entra questo con l'espansione dell'universo? Se sostituisci il tasso di crescita della distanza con il tasso di espansione, cioè la costante di Hubble ( che non è costante); sostituisci ad M la massa della materia uniformemente distribuita nel volume che si sta espandendo; ed al missile un pezzettino di materia che si allontana anche esso con l'espansione e l'analogia è fatta. La formula ottenuta è identica a quella ottenibile applicando la relatività nel caso di spazio piatto con predominanza della materia. Per l'iterpretazione corretta della formula occorre però riferirsi alla relatività.
con il tasso di espansione, cioè la costante di Hubble ( che non è costante); sostituisci ad M la massa della materia uniformemente distribuita nel volume che si sta espandendo; ed al missile un pezzettino di materia che si allontana anche esso con l'espansione e l'analogia è fatta. La formula ottenuta è identica a quella ottenibile applicando la relatività nel caso di spazio piatto con predominanza della materia. Per l'iterpretazione corretta della formula occorre però riferirsi alla relatività.
Ma figurati Fabrizio! Spiegato così va benissimo. L'importante è non cercare di scendere nei dettagli di un qualcosa che è ancora un argomento non risolto e che mette alla prova professionalmente le migliori menti. Pretendere di dare qui una risposta è a dir poco pretenzioso e ben lontano dall'umiltà di chi cerca di insegnare. Sai, sarebbe il primo passo verso quel tipo di forum dove c'è sempre qualcuno che dice: "Premetto di non sapere niente della relatività, ma ho avuto un'idea che spiegherebbe il tutto!"
Comunque, grazie per la cautela e per la chiarezza!