Categorie: Fisica classica
Tags: accelerazione gravità cinemtica moto uniformemente accelerato quiz
Scritto da: Vincenzo Zappalà
Commenti:29
QUIZ: un incontro in aria **
Cominciamo con la cinematica e con un esperimento veramente molto “pratico” ed eseguibile da tutti (con un po’ di pazienza).
Un veloce richiamo al moto uniformemente accelerato (ossia un moto rettilineo in cui la velocità è variabile, mentre l’accelerazione è costante). Per esso valgono le semplici equazioni del moto:
v = v0 + at
s = s0 + v0t + ½ at2
dove s0 e v0 sono la posizione e la velocità iniziali (se non sono uguali a zero), mentre a è l’accelerazione (costante). s e v descrivono le variazioni della posizione e della velocità in funzione del tempo. Le equazioni del moto si ricavano facilmente dalla definizione di velocità e accelerazione (come mostrato, ad esempio, nella “Fisica Addormentata nel Bosco”).
L’esempio più classico e famoso di un moto uniformemente accelerato è la caduta di un oggetto al suolo (la famosa mela di Newton).
Il problema di cinematica che vi propongo è veramente facile, ma può servire per prendere dimestichezza con le basi stesse della fisica. Chiedo, ovviamente, ai più preparati di tacere, mentre stimolo i meno preparati a “provare” senza preoccuparsi dei risultati. Il non sapere o lo sbagliare sono i primi passi fondamentali per la conoscenza.
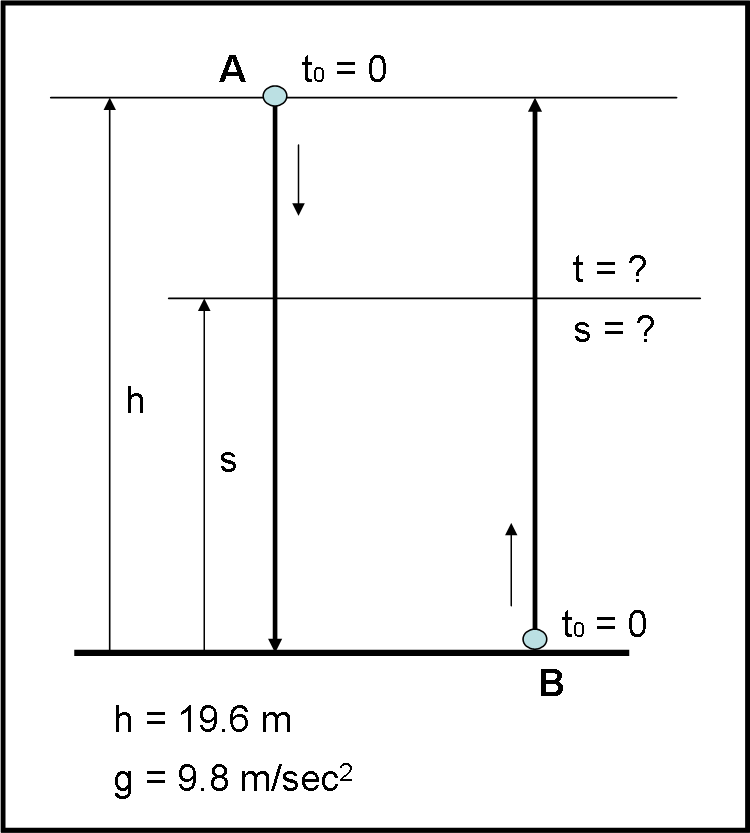
Immaginiamo di avere due persone con una pallina in mano. Il primo (A) si trova a un’altezza h = 19.6 m, mentre il secondo (B) è al suolo. Ammettiamo che non esistano attriti di nessun tipo. Nello stesso istante in cui A lascia cadere la sua pallina, B lancia la propria verso l’alto in modo perfettamente verticale, imprimendogli una velocità, costante, tale che possa raggiungere, ma non superare, l’altezza h.
Vi chiedo: “Quanti secondi dopo il lancio, contemporaneo, si incontrano le due palline e a quale altezza s dal suolo?”
Ovviamente, conosciamo anche l'accelerazione di gravità che consideriamo costante e vale g = 9.8 m/sec2
Non datemi solo i "numeri" finali, ma anche la descrizione dei vari passaggi... Riporto anche una banale figura esplicativa
Buon lavoro e fatevi sentire in molti.
QUI la soluzione






29 commenti
ssssssssshhhhhh!!!!!!!!!!!!!
comunque, Alvy, se vuoi mandarmi la soluzione in via privata la accetto volentieri. Ci sono vari modi per risolverlo e mi piacerebbe sapere quale hai scelto tu (almeno lo imparo e poi posso scriverlo per tutti ). Ah, questi supplenti!!!!!
). Ah, questi supplenti!!!!! 
Forza ragazzi, datevi da fare!!! Senza fisica elementare è inutile parlare di MQ & co.....
hai ragione enzo pero' per me e' gia' impegnativo, ho bisogno di un tavolo su cui sedermi e fare i conti...
Questo pomeriggio o piu' probabilmente domani pomeriggio provo a scrivere le mia soluzione....
Ciao Enzo, anzitutto grazie per aver eliminato le circonferenze dai quiz
Posso darti la soluzione o aspetto?
Caro Enzo, penso di aver trovato un modo per risolvere il problema, ma non so se esporlo o aspettare.
Come hai giustamente intuito ho diverse lacune da colmare in questo campo (per cui non è detto che la soluzione sia corretta), però non vorrei togliere spazio ad altri, per cui dimmi tu se attendere (se questo serve per stimolare molte altre risposte attendo volentieri )..
)..
Paolo
Le palline si incontrano dopo un secondo a 14.7 metri da terra:
La velocità con cui deve partire la pallina da terra è: v = (2 s g)^1/2 = 19.6 m/sec
L'altezza di incontro delle palline è:
dal basso: s = vt - 1/2 g t^2
dall'alto: s = 19.6 - 1/2 g t^2 sostituendo questa nella prima, trovo: 19.6 = vt da cui
t = 19.6/v = 1 sec
e quindi l'altezza: s = 19.6 - g/2 = 14.7 m
per perfetta simmetria a meta' altezza
Ciao Silvano
Caro Silvano, non hai torto a parlare di simmetria. In effetti a metà strada qualcosa di comune accade, ma non l'incontro!
Aspettiamo ancora un po'... ma inviterei coloro che l'hanno risolto a scriverlo pure. L'interessante è anche vedere con quale sistema è stato risolto... ne ho pronti altri di molto carini (senza cerchio per adesso... ).
). ).
).
Scusate se abuso un po' con i quiz... ma mi impegnano poco e riesco a pubblicarli facilmente tra un'andata all'ospedale e l'altra. Tuttavia, tutto va bene e i progressi continuano (oggi le ho dato da mangiare io!!!
Buon weekend a tutti!!!!
Per trovare una soluzione al quiz, ho provato ad analizzare il moto delle due palline.
Al tempo T0, la pallina A è ferma, ossia la sua velocità iniziale Vo è uguale a zero, appena viene lasciata cadere viene accelerata dalla forza di gravità, fino a raggiungere il suolo ad un certa velocità, dopo un certo intervallo di tempo.
Durante il tragitto la velocità della pallina varia, ossia subisce un'accelerazione costante, pari a g (accelerazione di gravità).
Trattandosi di moto accelerato uniforme:
S = S0 + V0 t + ½ a t^2
Ponendo S0 = 0 (partendo dall'altezza h per andare verso il suolo) e V0 = 0 (la pallina è ferma)
S = ½ g t^2
Dunque la pallina A per arrivare al suolo, ossia per percorrere lo spazio h (altezza dal suolo), impiega:
h = ½ g t^2
t^2 = 2 h/ g
t = (2 h/ g) ^ ½ = (2 19,6 / 9,8 ) ^ ½ = ( 39,2/9,8) ^ ½ = (4) ^ ½ = 2 secondi
Cosa succede alla pallina B?
Al tempo T0 la pallina viene portata a una certa velocità, solo che ora la forza di gravità frena il moto della pallina, fino ad arrestarlo all'altezza h dal suolo, dove la sua velocità per un'istante è uguale a 0 (dopodichè ricade irrimediabilmente al suolo).
Mentre la pallina A trasforma una parte della sua Energia di potenziale in Energia cinetica, acquistando velocità, il moto della pallina B è dovuto ad una forza esterna che le imprime una certa velocità in direzione verticale rispetto al suolo.
Tale Energia esterna è sufficiente per vincere la forza di gravità solo fino all'altezza h dal suolo.
In quel punto la pallina A possiede un'energia di potenziale di:
Epot = mgh
La sua Energia cinetica è nulla, poiché nell'istante iniziale la pallina è ferma.
L'energia Totale è in quel punto pari a:
Etot = mgh + 0 = mgh
Quando la pallina cade al suolo, ha una certa velocità, ed una certa Energia cinetica:
Ec= ½ m v^2
l'Energia Totale è uguale a:
Etot = mg 0 + Ec = Ec = ½ m v^2
Dato che l'Energia Totale della pallina A non può cambiare (non ha subito alcun forza esterna, ma solo quella di gravità)
Etot = mgh = ½ m v^2
per cui
mgh = ½ m v^2
gh = ½ v^2
2gh = v^2
v = (2gh) ^1/2 = (2 9,8 19,6) ^1/2 = 19,6 mt/sec
Questa dovrebbe essere la velocità con cui la pallina A arriva al suolo.
La pallina B per arrivare fino all'altezza h dovrà possedere un'energia che le consente di contrastare il movimento verso il suolo dovuto alla forza di gravità.
Tale Energia, diventa uguale a zero, quando la pallina B arriva all'altezza h.
Perciò il valore di tale Energia non può che essere uguale a quella di potenziale della pallina A al tempo zero, e quindi vale tanto quanto la sua energia cinetica (anche se di segno opposto)
Ne segue, che la velocità iniziale da impartire alla pallina B è pari a quella appena trovata:
v = (2gh) ^1/2 = 19,6 mt/sec
Al medesimo risultato si poteva arrivare senza scomodare le Energie.
Partendo dalla relazione:
S = S0 + Vo t + ½ at^ 2
Ponendo So = 0, (partendo dal punto B, ossia il suolo), Vo = velocità iniziale della pallina B e cambiando di segno l'accelerazione (che si contrappone al moto di B):
Lo spazio percorso dalla pallina B, nel tempo è pari a :
Sb = Vo t - ½ gt^ 2
Lo spazio percorso dalla pallina A (partendo dall'alto) nel tempo è pari a:
Sa = ½ gt^ 2
Quando i due percorsi si trovano alla stessa altezza dal suolo si realizza la seguente condizione:
h = Sa + Sb dove Sa è lo spazio percorso da A e Sb quello da B
Per cui, sostituendo a Sa e Sb i valori trovati, si ha:
h = Vo t - ½ gt^ 2 + ½ gt^ 2
h = Vo t
Vo = h/t = 19,6 mt/ 1sec
Quindi dopo 1 secondo lo spazio percorso dalla pallina B (partendo dal suolo) è pari a:
Sb = Vo t - ½ gt^ 2 = 19,6 - ½ 9,8 = 19,6 - 4,9 = 14,7 metri
Lo spazio percorso dalla pallina A (partendo dall'alto) dopo un secondo è pari a:
Sa = ½ gt^ 2 = - ½ 9,8 = 4,9 metri
giusto per conferma:
h = Sa + Sb = 14,7 + 4,9 = 19,6 metri
Dunque entrambe le palline, dopo 1 secondo, si trovano alla medesima distanza dal suolo di 14,7 metri.
Per la pallina B questa corrisponde allo spazio percorso in 1 secondo, per la pallina A alla differenza tra l'altezza di partenza h e lo spazio percorso in 1 secondo (19,6 – 4,9 = 14,7 metri).
Qualcuno parlava di simmetria, in un certo senso anche a me sembra che non ha tutti i torti, però non si tratta di un comportamento linearmente speculare quello tra A e B,ossia non sono due palline che in assenza di gravità si muovono alla stessa velocità costante,.
Infatti mentre A accelera, B decelera, A parte da velocità zero e raggiunge la massima velocità al suolo, B parte con la stessa velocità di A quando raggiunge il suolo ed arriva all'altezza h decelerando fino a velocità zero.
Tutte e due le palline impiegano 2 secondi per percorrere lo spazio h (altezza dal suolo).
Per mostrare cosa intendo per comportamento speculare, ma inverso, parto dalle relazioni appena trovate.
Dopo 1 secondo la pallina A ha percorso 4,9 metri e la pallina B 14,7 metri.
Proviamo a invertire le parti, per cui ora è la pallina A che deve percorrere 14,7 metri.
S = ½ gt^2
Dato che S = 14,7 mt:
t = (2 S /a) ^ ½ ( 2 14,7 / 9,8) ^ ½ = (3)^ ½ = 1,732 secondi
Ora questo tempo lo chiamiamo ta.
Dato che per percorrere l'intero tratto la pallina A (come la B) impiega 2 secondi, per percorrere i rimanenti 4,9 metri che la separano dal suolo impiega:
2 secondi – 1,732 secondi = 0.268 secondi
Il tempo trovato non è altro che tb, ossia il tempo da utilizzare affinché la pallina B percorra 4,9 metri (situazione inversa rispetto a quella iniziale)
Sb = Vot – ½ gt^2
Usando come tempo tb, si ha:
Sb = 19,6 0,268 - ½ 9,8 0,268^2 = 5,2528 – 0,3519 = 4,9 metri
Esattamente la situazione inversa rispetto a quella iniziale (t = 1 secondo), solo che la pallina A ha impiegato ben 1,732 secondi per percorrere 14,7 metri, mentre la pallina B ha impiegato 0,268 secondi per percorrere 4,9 metri.
La relazione trovata tra ta e tb, dovrebbe funzionare, quindi, anche a metà del reciproco percorso, ossia h/2 = 9,8 metri.
S = ½ g t^2
Dato che S =9,8 mt:
t = (2 S /a) ^ ½ ( 2 9,8 / 9,8) ^ ½ = (2)^ ½ = 1,414 secondi
tb = 2 secondi – 1,414 secondi = 0,586 secondi
Sb = Vot – ½ gt^2
Sb = 19,6 0,586 - ½ 9,8 0,586^2 = 11,4856 – 1,6826 = 9,8 metri
Sembra proprio funzionare.
Paolo
Per trovare la velocità di lancio della pallina da terra, considerato che la somma tra energia potenziale e cinetica deve essere costante, deve essere: gmh = 1/2mv^2
da cui si ottiene che h = v^2/2g e ponendo h=19,6 e sostituendo abbiamo v =19,6m/sec
Le due palline si incontreranno quando la somma delle distanze percorse è uguale ad h (cioè 19,6m) e quindi avremo Sa + Sb = 19,6m
Sa = 1/2gt^2
Sb = vt - 1/2gt^2
quindi:
1/2gt^2 + vt - 1/2gt^2 = 19,6
vt = 19,6 e quindi t = 1 (dopo 1 secondo le palline sono alla solita altezza)
sostituendo in Sa abbiamo: Sa = 1/2*9,6 = 4,8 metri
sostituendo in Sb abbiamo: Sb = 19,6 - 1/2*9,6 = 14,8 metri
Logicamente la pallina che parte dall'alto (Sa) si troverà a 19,6 - 4,8 (distanza percorsa) = 14,8 metri, anch'essa dopo 1 secondo si troverà alla stessa altezza di Sb.
Ottimo ragazzi!
A questo punto chi vuole provare può fare a meno di guardare i vostri risultati e controllare solo alla fine. Devo aggiungere, per onestà, che anche Alvy ha risposto esattamente (l'ha fatto in privato come gli avevo chiesto...).
Posso solo aggiungere che il discorso energetico può essere trascurato, dato che il problema è di pura cinematica e basta considerare, come fatto da quasi tutti, le leggi del moto.
Se non vi dispiace, continuerei a proporre alcuni esercizi di questo genere e poi magari li mettiamo assieme e possono sempre servire. Che ne dite? D'altra parte, ho visto che il numero di lettori è abbastanza alto e quindi vuol dire che, rispondendo oppure no, sembrano comunque stimolare l'interesse.
Non devo faticare tanto e mi serve poco tempo, in attesa di riuscire ad aumentarlo insieme alla tranquillità...
Scusa SuperMagoAlex mi sono chiesto perchè hai ottenuto risultati diversi..... penso che nelle relazioni finali hai usato come valore di g 9,6 invece di 9,8 m/sec^2... dagli un occhio.
Buona domenica
Paolo
nooo che vergogna non ci riesco!
da s = s0 + v0t + ½ at^2 ho trovato che la pallina cade in 2 secondi, infatti diventa:
19,6=0+0+4,9t^2 da cui t^2 = 4 e t = 2
per trovare la velocità con cui viene lanciata la pallina ho modificato la formala da s = s0 + v0t + ½ at^2 in s = s0 +v0t - ½ at^2 in quanto la pallina è sottoposta a un moto decelerato uniformemente e non più accelerato e mi diventa:
19,6 = 0+v0*2-4,9*4 da cui ricavo 2v0=39,2 e quindi v0=19,2
Adesso però non riesco a mettere insieme i dati ricavati per risolvere il problema, copierò da paolo che è sempre chiaro nelle spiegazioni...
Insomma rimandato a settembre (per non dire bocciato)!
Alex guarda che hai solo toppato un calcolo:
S= S0 + Vot - 1/2 a t^2
t = 2 secondi S = h = 19,6 metri a = 9,8 m/sec^2 So = 0
h= 0 + Vo 2sec - 1/2 9,8 2^2
19,6 = 2Vo - 1/2 9,8 2^2
19,6 = 2 Vo - 4,9 4
19,6 = 2Vo - 19,6
19,6 +19,6 = 2 Vo
39,2 = 2 Vo
Vo = 39,2 /2 = 19,6 m/sec
39,2 diviso due fa 19,6 e non 19,2
Paolo
Scusa Alex, invece di copiare che non serve a molto, prova a vedere se questa figura che fissa una condizione importante, può risultarti utile per risolvere il quiz.
http://www.astrobin.com/full/34209/F/
Paolo
Ho calcolato che la pallina lasciata cadere da A, senza attriti, raggiunga il suolo in 2 secondi (19.6/9.8=2 sec )
A questo punto B dovrà lanciare verso l'alto la pallina ad una velocità che le permetta di superare l'attrazione gravitazionale e in più di raggiungere i 19,6 mt di altezza nello stesso tempo che A ha impiegato per raggiungere il suolo.
Quindi 9,8+9,8=19,6 ms
A questo punto mi blocco perchè se considero l’assenza di attriti, le due palline dopo 1 secondo si incontrano a metà strada ossia ad 1 mt di altezza, perché avranno la stessa velocità, una di caduta e l’altra di salita. (???)
Ma potreste spiegarmi per favore perchè nella formula è indicato Sb = Vot – ½ gt^2 e il valore di attrazione gravitazionale è dimezzato? Aiuto


Nella relazione del moto accelerato uniforme.
S = S0 + Vot + 1/2 a t^2
Sia Vot, sia 1/2gt^2, non sono altro che misure di spazio percorso in un certo tempo.... non è la gravità che viene dimezzata, semplicemente 1/2 a t^2 indica quanto spazio nel tempo percorre un corpo (fermo) sottoposto ad un accelerazione costante (in questo caso quella di gravità), ovviamente se il corpo non è fermo lo spazio percorso dipende anche dalla velocità inziale V0 (nel caso della pallina B questa possiede una velocità inziale e l'accelerazione si contrappone al moto per cui va sottratta - 1/2 a t^2) .
Paolo
Non voglio mettere il naso più di tanto... Attenta Gio che hai trovato la velocità della pallina all'inizio, ma mentre sale rallenta... Mentre l'altra aumenta la velocità ma parte con v = o. Tutto sta nel trovare una relazione che lega g,h e il tempo con s...
Molte risposte sono esatte e qualcuna anche elegante e rapida... Il risultato può essere visto dalle risposte, ma lascio ancora un po' di tempo per chi vuol provare...
Intanto ne preparo uno più semplice...
La formula che non convince Gio si deriva pari pari dal moto di un corpo uniformemente accelerato e dalle definizioni di velocità e accelerazione (al limite ricordandosi di fare una media delle velocità di partenza e di fine percorso..., da cui il valore 1/2). Magari un giorno spiegheremo anche la cinematica, ma si trova tutto sulla Fisica addormentata nel bosco...
Infatti era proprio questo il mio dubbio, se lancio una pallina verso l'alto all'inizio della corsa avrà una velocità maggiore rispetto alla fine... Ora mi studio meglio le formule....
scusate tutti... ma in questo periodo riesco a fare poco di più e... faccio lavorare voi!
Comunque, le cose vanno bene e da un giorno all'altro dovrebbero eliminare tutti i vari tubi... Bisogna darle da mangiare, però... e preferiamo farlo noi...
Questi esercizi verranno utili, li metteremo tutti assieme e saranno sempre a disposizione per chi vuole mettersi alla prova. Quanto prima spero di ricominciare con la relatività, ma devo avere più tempo e più concentrazione...
Ancora un po' di pazienza...
@Paolo
Si è vero, ho usato un pò 9,6 e un pò 9,8... potevo fare una media sui 9,7
grazie Paolo per il suggerimento, infatti se poi dopo inserisco la condizione che lo spazio totale percorso (19,6 metri) corrisponda alla somma dello spazio percorso dalla pallina A e quello percorso dalla pallina B allora tutto mi torna.
A pensarci bene era ovvio, io mi perdevo facendo la sottrazione e non la somma (chissà perchè)...
Diventa 19,6 = 19,6*t - 1/2at^2 + 1/2at^2 e quindi 19,6 = 19,6* t e quindi t =1
Sostituendo 1 in s0 + v0*t - 1/at^2 ottengo: 0 + 19,6 - 4,9 che diventa 14,7.
La pallina lanciata dal basso deve fare 14,7 metri
Quella dall'alto 1/2*9.8*1 = 4,9
La somma 14.7+4.9=19.6.
L'incontro avviene dopo 1 secondo.
Insomma non ho saputo intuire da solo la chiave per risolvere l'enigma
Ho provato diversi metodi per risolvere il quiz ed a mio avviso questo è il più rapido.
Tempo per percorrere h
Pallina A
h = ½ g t^2
t = (2h/g)^ ½ = ( 2 19,6/ 9,8)^ ½ =2 secondi
Dato che anche la pallina B ci mette 2 secondi per percorrere lo spazio h
h = Vot – ½ gt^2
h = 2Vo – ½ g 2^2 = 2Vo – ½ g 4 = 2Vo – 2 g
2Vo = h + 2g
Vo = h/2 + g = 19,6/2 + 9,8 = 9,8 + 9,8 = 19,6 m/sec
Per trovare il tempo che impiegano le due palline per trovarsi alla stessa altezza dal suolo conviene analizzare il moto usando lo stesso sistema di riferimento, ossia con il suolo come origine.
Per cui, le relative altezze dal suolo sono:
Pallina A
ha = h – 1/2gt^2
Pallina B
hb = Vot – ½ gt^2
Dato che dobbiamo trovare quando le palline hanno la medesima altezza dal suolo, tradotto significa che ha = hb
h – 1/2gt^2 = Vot – ½ gt^2
h = Vot
t = h/Vo = 19,6/19,6 = 1 secondo
Una volta trovato il tempo (1 secondo) impiegato da ogni pallina per raggiungere la medesima altezza dal suolo, è semplicissimo calcolare il valore di tale altezza
Pallina A
ha = h – 1/2gt^2 = 19,6 – ½ 9,8 1^2 = 19,6 -4,9 = 14,7 metri
Pallina B (per conferma, dato che ha=hb):
hb = Vot – 1/2gt^2 = 19,6 1 - ½ 9,8 1^2 = 19,6 – 4,9 = 14,7 metri
Una piccola domanda di ordine matematico: ammettiamo che ci sia solo la pallina B, come è possibile ricavare il tempo partendo dalla relazione del moto:
S= Vot – ½ gt^2
Senza introdurre altre relazioni non sono riuscito a risolvere questa equazione ricavando il tempo. ..
..
Paolo
caro Paolo,
se ho capito bene il tuo problema, è necessario conoscere almeno due variabili: la velocità di partenza e l'altezza di arrivo. La tua equazione deve essere risolta rispetto a t. E' di secondo grado e avrà due soluzioni, di cui sarà da escludere... Prova a fare un esempio e poi vedi cosa ti viene...
Ormai la risposta è di dominio pubblico... Penso, comunque, di riassumere la risposta in un articoletto, in modo che sia sempre facilmente a disposizione. Ne approfitto anche per fare un richiamo a come si determinano le equazioni del moto... OK?
Mi metto al lavoro... e poi inserisco un nuovo quiz MOOOOOOLTO semplice, proprio per i meno esperti!
A dopo...
Caro Enzo hai capito benissimo (ovviamente V0 e S, l'altezza di arrivo, devono essere noti)....
Gulp non ho ancora letto il tuo articolo sulle equazioni di secondo grado ed è passato troppo tempo per ricordarmi quando le ho studiate a scuola, per cui non mi resta che trovare un po' di tempo e studiarmi le equazioni di secondo grado.
Grazie.
Paolo