Il presente articolo è stato inserito nelle pagine d'archivio  "Quattro passi nella storia della Scienza"

 

A volte si pensa: "Ma come ha fatto Keplero a enunciare tre leggi praticamente perfette pensando e tracciando poliedri e sfere che li racchiudevano?". In realtà il modello kepleriano del Sistema Solare sembra più un gioco di incastri, cosparso di un forte sapore esoterico. Non per niente, la base di tutto è la visione filosofica di Platone e quella mistica e geometrica di Pitagora. Ma proprio questa simbologia, apparentemente risibile per occhi moderni, ha fatto scattare varie molle di puro intuito scientifico, provocando una rivoluzione epocale, quasi paragonabile a quella einsteniana.

L'uomo e le dimensioni

In campo puramente geometrico lo spazio in cui è immerso l'uomo, o -forse più correttamente- che è percepito dall'uomo, è decisamente ridotto: solo tre dimensioni! Escludiamo il tempo in quanto ci farebbe entrare in ambito relativistico e non è certo questo il nostro scopo.

Avesse dimensione UNO sarebbe costretto a vivere su una linea (retta o curva ha poca importanza); con uno spazio a DUE dimensioni vivrebbe in un piano; con lo spazio a TRE dimensioni entra decisamente in un volume, ciò che viene anche comunemente chiamato "spazio". Gli assi cartesiani individuano in modo molto semplice e sintetico questa diversificazione, ovvero questa scalata verso dimensioni maggiori. La matematica ci permette di entrare abbastanza facilmente in spazi superiori (come l'ipersfera), ma resta un qualcosa di teorico o  -se preferite- di irraggiungibile per i nostri sensi. Non per altro la rappresentazione dantesca del mondo, percepibile solo alle anime elette, è probabilmente proprio un'ipersfera che Dante riesce a "vedere" solo attraverso gli occhi di Beatrice, ormai anima del Paradiso.

Torniamo, perciò, alla realtà in cui viviamo e saltiamo indietro di qualche secolo (in realtà tanti secoli) e affacciamoci alla Scuola Pitagorica. Tutto ciò che esiste ha la sua origine nei numeri, che ne permettono una descrizione globale.

Il punto corrisponde al numero UNO e viene inteso come "spazio" senza dimensioni. Il DUE corrisponde a un segmento che definisce UNA dimensione; il TRE permette di costruire un triangolo che definisce le DUE dimensioni; il QUATTRO permette di costruire il tetraedro che porta alle TRE dimensioni. Questa è la base della Tetraktis, il quartetto divino, i primi 4 numeri interi, che danno come somma il 10, il numero che indica l'intero Universo. La stessa  scuola portava questo nome e i suoi discepoli prestavano giuramento sulla Tetraktis. Il numero dieci che è rimasto sempre tra i "favoriti" in moltissime culture: il 10 è  considerato simbolo di pace e di fratellanza, infatti, con una stretta di mano, due persone uniscono fra loro le dieci dita; i Comandamenti divini sono 10; o, ancora più semplicemente, il 10 è il voto più bello che si può prendere a scuola...

Il triangolo e il divino numero dieci

I primi 4 numeri, la loro somma, il triangolo... legami indissolubili associati alla divinità, alla creazione, al Tutto. Lo stesso Dante (Convivio 2, XIV, 3) aveva questa idea del dieci, come numero perfetto:

Dal diece in su non si va se non esso diece alterando cogli altri nove e con sé stesso.

Basta riportare 10 punti come fatto nella Fig. 1 e vediamo subito una rappresentazione illuminante e geniale.

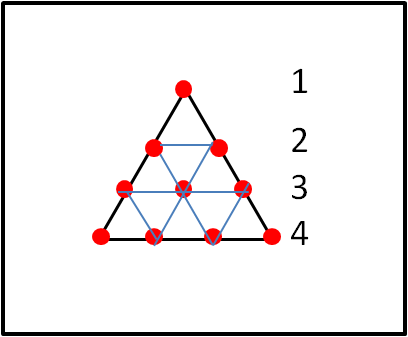
Con questo intreccio di teoria e di magia dei numeri, di simboli esoterici, di setta religiosa e di comunità scientifica, la figura di Pitagora  può essere vista come filosofo e matematico, ma anche come profeta e mago e la sua comunità come scuola, ma anche come setta segreta.

Scrive Bertrand Russell: "Sono i due aspetti di Pitagora, il profeta religioso e il matematico puro. Da entrambi i punti di vista ebbe una incommensurabile influenza, e i due aspetti non si possono separare come potrebbe credere una mente moderna". Questa frase fa già capire come certe conquiste scientifiche degli antichi debbano essere sapute leggere, a volte, attraverso simbologie di carattere  religioso o filosofico o mistico.

Armonia, Bellezza e Natura attraverso la Geometria

L'influenza esercitata dai pitagorici risultò fondamentale per lo sviluppo della filosofia greca classica e del pensiero medioevale europeo. Nel Rinascimento alcune idee dei pitagorici, come la Tetraktis o le proporzioni armoniche, vennero ampiamente applicate anche in campo artistico. Lo stesso Copernico dichiarava che il suo sistema, con il Sole nel centro, era un sistema pitagorico così come Galileo era considerato pitagorico in quanto il grande greco  era visto come il padre di tutte le scienze esatte.

Ma torniamo a Pitagora, ai suoi numeri e alle loro rappresentazioni geometriche.

Particolare importanza aveva sicuramente il triangolo, attraverso cui si arriva facilmente ai poliedri regolari, che è lo scopo del nostro articolo. Un triangolo può essere di diverso tipo, in particolare  equilatero, la figura armonica per eccellenza, che, tuttavia, ha la sua origine da un triangolo scaleno, quello giudicato il più "bello" tra di loro. Esso non è altri che il triangolo rettangolo con un lato che è la metà dell'ipotenusa (quanta importanza avrà in seguito lo sappiamo benissimo... è sufficiente chiedere ad Euclide, ad esempio). Basta duplicarlo e, unendo i due "fratelli", si ottiene proprio il triangolo equilatero (Fig. 2).

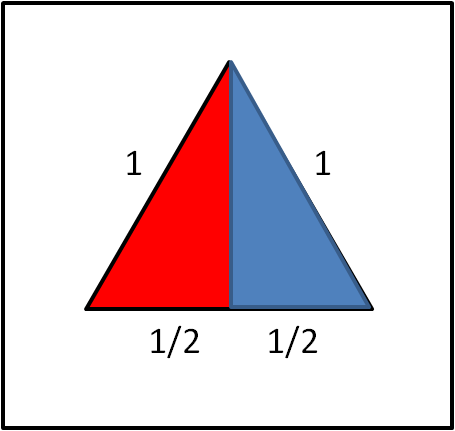
Non è molto da meno il triangolo isoscele, che sotto alcune forme particolari, assume un ruolo fondamentale per creare il quadrato (due triangoli isosceli rettangoli). Più complessa e articolata è la formazione del pentagono. Esso si ricollega facilmente alla stella a cinque punte, altro simbolo divino per i pitagorici (pentagramma) e al numero aureo.

Disegniamo un pentagono regolare e prolunghiamo ogni lato fino a formare la punta della stella, oppure tracciamo tutte le diagonali di un pentagono fino a incontrarsi tra loro (come fatto in Fig. 3).

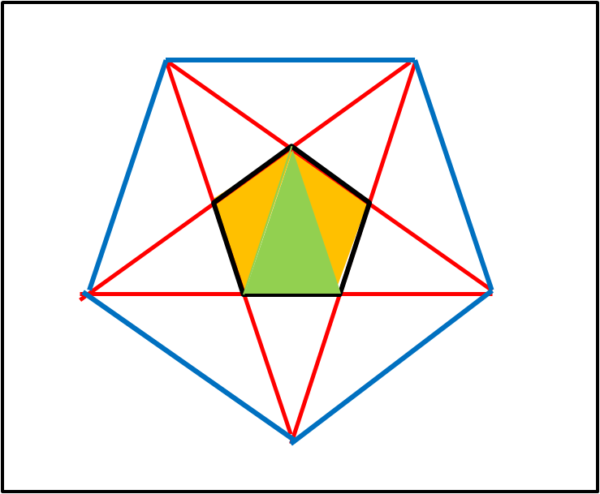
Le punte che escono dal pentagono centrale o che toccano i suoi vertici, sono particolari triangoli isosceli, per la precisione triangoli "aurei", nel senso che i lati uguali stanno a quello minore come il rapporto aureo. Ma lo stesso triangolo aureo (verde) si ottiene tracciando due diagonali del pentagono che partono dallo stesso vertice. I due triangoli isosceli rimanenti (arancione) prendono  il nome di gnomoni aurei (in questo caso il rapporto è quello inverso a prima).

I solidi platonici

Fatte queste dovute premesse, passiamo ai poligoni regolari. Essi sono infiniti, dato che possiamo aumentare quanto vogliamo il numero dei lati, mantenendoli uguali a se stessi e ottenere sempre una figura che abbia anche gli angoli interni uguali; in altre parole, una figura che sia inscrivibile e circoscrivibile in/da una circonferenza. Sappiamo bene che se il numero dei lati tende a infinito, il poligono tende a sovrapporsi alle due circonferenze. Noi, però, vogliamo fare il passo successivo e costruire un poliedro, ossia una figura tridimensionale chiusa e convessa che abbia tutte le sue facce uguali tra loro e che queste siano anche poligoni regolari.

La prima impressione potrebbe essere quella di dire: "Ce ne sono infiniti..." E, invece, no! Sono molti meno, in particolare solo CINQUE. Essi vennero quasi sicuramente definiti dai pitagorici, ma divennero famosi per l'interpretazione metafisica che ne diede Platone. Non per niente prendono anche il nome di Poliedri (o solidi) Platonici.

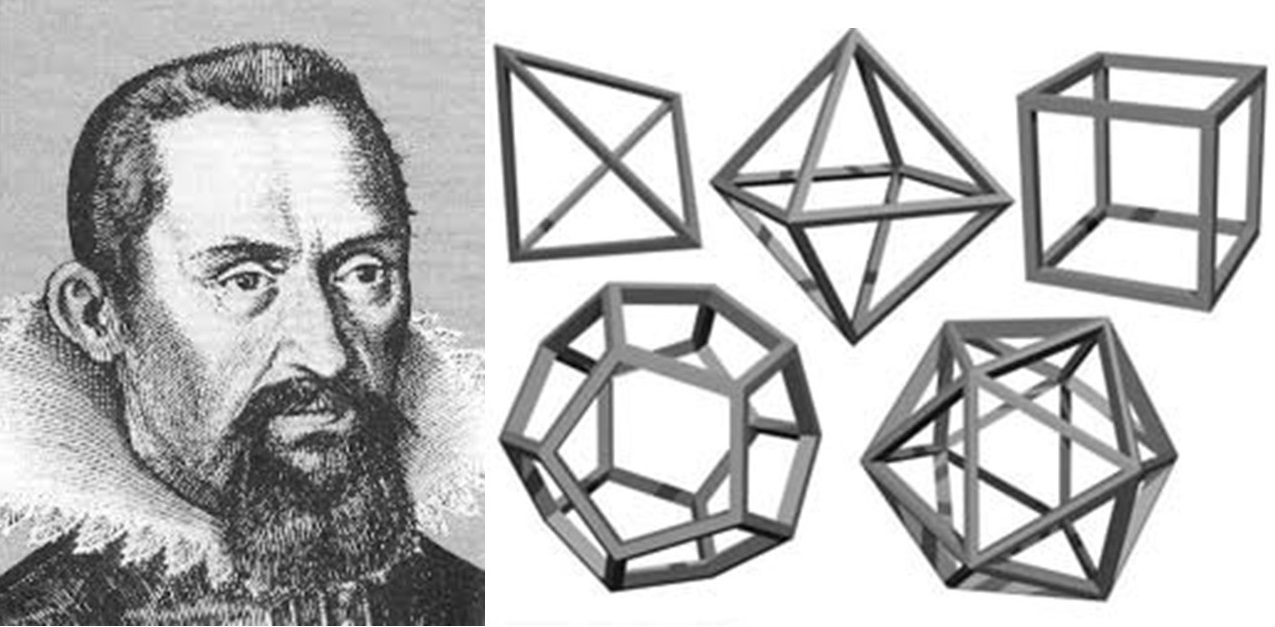
Prima di vederli da vicino, dimostriamo facilmente che essi non possono essere più di cinque. Utilizziamo il fatto che solo pochissimi poligoni regolari possono diventare le loro facce. Ogni poliedro deve avere dei vertici in cui confluiscano almeno tre facce, altrimenti ricadremmo in una figura piana. Lo spazio racchiuso da queste tre facce può essere chiamato angoloide. Esso, perciò, deve essere formato da poligoni che abbiano un angolo al vertice tale che la somma di tre o più di loro sia sempre MINORE di 360° Se la somma fosse 360° le facce convergenti nel vertice del poliedro sarebbero complanari e il solido cadrebbe nelle due dimensioni. Nel caso dei poliedri regolari le facce devono essere tutti poligoni uguali e, di conseguenza, la somma di un certo numero di angoli uguali a se stessi deve essere inferiore a 360°.

Riassumiamo: (a) ci vogliono almeno TRE facce per formare un angoloide; (b) la somma degli angoli delle facce che formano l'angoloide deve essere minore di 360° (c) le facce devono essere poligoni regolari, con angoli interni tutti uguali tra loro, e quindi, dovendo essere almeno TRE e non dovendo superare come somma 360°, il poligono con più lati da poter considerare deve avere un angolo MINORE di 120° (120 x 3 = 360).

Cominciamo, allora a selezionare i nostri poligoni e cerchiamo di farli diventare delle facce di un poliedro regolare, ossia platonico.

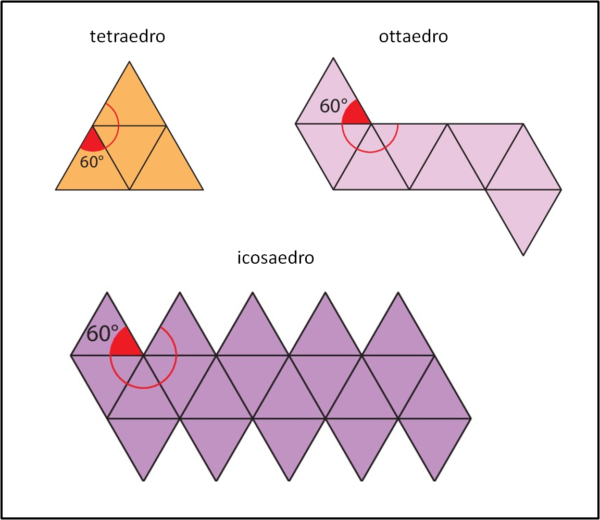
Il primo poligono è sicuramente lui, simbolo di perfezione, il triangolo equilatero. Quanto misura l'angolo al vertice di un triangolo equilatero? Facile... 60°. Il che vuol dire che non solo ci possiamo permettere di costruire un angoloide con tre triangoli equilateri convergenti in uno spigolo (60 x 3 = 180), ma anche con quattro (60 x 4 = 240) e addirittura con cinque (60 x 5  = 300).

Il primo è il più immediato e porta al tetraedro: 4 facce uguali a triangoli equilateri, ricollegandosi subito alla Tetratkis. Passando a 4 facce si costruisce ancora facilmente un solido con 8 facce, l'ottaedro. Concludiamo con il solido più elaborato: l'icosaedro, con ben 20 facce. Di tutti e tre possiamo vedere lo sviluppo su un piano in Fig. 4 (disegnando e ritagliando si possono facilmente costruire...).

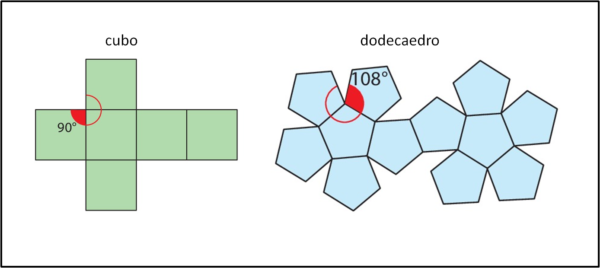
Un altro poligono regolare che può essere utilizzato è il quadrato, il cui angolo è 90°. Tuttavia, non possiamo superare le tre facce per angoloide: 3 x 90 = 270, ma 4 x 90 = 360 (troppi). Beh... il poliedro che deriva dal quadrato (che ricordiamo è composto da due triangoli isosceli rettangoli) è forse il più celebre per tutti noi: il cubo con le sue 6 facce.

Andiamo oltre e passiamo al pentagono. E' ancora possibile utilizzarlo? Sicuramente sì, dato che il suo angolo interno è 108° e 108 x 3 = 324°. Anche per lui, però, è l'unica possibilità, dato che 108 x 4 = 432 > 360°. Otteniamo il dodecaedro con 12 facce.

In Fig. 5 vediamo gli sviluppi su un piano anche di questi due ultimi poliedri regolari.

Di seguito, invece, una loro animazione molto ... "solida".

Il dodecaedro è sempre stato considerato il punto di arrivo, il solido per eccellenza, la cui forma era considerata da Platone la forma stessa dell'Universo.

I poliedri regolari o platonici hanno assunto un'importanza fondamentale pur nella loro semplice struttura geometrica. Platone li associa agli elementi: il tetraedro rappresenta il Fuoco; il cubo la Terra; l'ottaedro l'Aria e l'icosaedro l'Acqua. Il dodecaedro, come già detto, l'Universo, il Tutto. Una visione non tanto religiosa quanto armonica che ha sconfinato facilmente in tutte le arti "belle", come la musica, l'architettura, la pittura, ecc. Un mezzo per legare microcosmo e macrocosmo, dato che negli stessi cristalli che formano molti composti chimici si ritrovavano le stesse forme.

Una visione in qualche modo esoterica che non poteva non fare breccia negli astrologi e colleghi vari (ancora oggi gli elementi platonici sono tenuti in alta considerazione), ma che era facilmente applicabile alle armonie della Natura e alle opere dell'uomo. Leonardo li aveva disegnati per il trattato  di Luca Pacioli sulle Divine Proporzioni e Piero della Francesca per la sua ossessionante ricerca della metrica perfetta. Perfino Salvator Dalì si è richiamato spesso ai poliedri regolari e soprattutto al dodecaedro.

Dalla visione filosofica di Platone alla rivoluzione scientifica di Keplero

Ma a noi quello che interessa di più è il risvolto astronomico che è stato fondamentale nel lavoro di Keplero. Sembra quasi impossibile che la definizione di tre leggi veramente rivoluzionarie e assolutamente perfette (nei limiti delle conoscenze di allora e per molti secoli dopo) partisse proprio dalla ricerca dell'armonia platonica e dall'ossessione di riportare tutto il Cosmo nell'ambito di una metrica rigorosa. Copernico, in fondo, aveva solo spostato il Sole al centro, ma molte cose restavano ancorate al passato, compresi gli epicicli che cercavano di superare la difficoltà di mantenere i moti sempre e soltanto circolari. Keplero vuole fare di più e lo vuol fare cercando di impostare il tutto sulla base dei poliedri regolari. Provando e riprovando, a volte deriso e spesso costretto a ricominciare da capo, alla fine riesce a trovare la situazione ottimale dalla quale, quasi "per caso", derivano le sue leggi. In parole semplici, anche per Keplero la Terra rimaneva un pianeta "particolare" più importante degli altri. Il suo eliocentrismo portato verso la perfezione, rimaneva in qualche modo un geocentrismo psicologico. Alla Terra doveva in qualche modo essere associato il dodecaedro, il solido di massimo valore. E così, allora, ecco la sua soluzione che gli diede quasi totale soddisfazione.

"L'orbita della Terra è la misura di tutte le cose. Si circoscriva attorno ad essa un dodecaedro, e il "cerchio" che lo contiene è l'orbita di Marte; attorno a Marte si circoscriva un tetraedro, e il cerchio che lo contiene è l'orbita di Giove; si circoscriva attorno a Giove un cubo, e il cerchio che lo contiene è l'orbita di Saturno. Poi si inscriva nell'orbita terrestre un icosaedro, e il cerchio contenuto sarà l'orbita di Venere, e ancora si inscriva all'interno dell'orbita di Venere un ottaedro e il cerchio contenuto sarà l'orbita di Mercurio." 

Egli dice, inoltre, una frase che appare modernissima:

Il vero miracolo non è che i numeri hanno effetto sulle cose, quanto piuttosto che essi possono esprimere la natura delle cose."

E ancora:

"L'essenza della mia posizione è presto detta: che gli astri abbiano una qualche influenza sulla gente lo si vede abbastanza con chiarezza, ma quale sia specificatamente questa influenza resta un mistero. […] Fra gli astri non c'è buono o cattivo, qui solo le categorie dell'armonia, del ritmo, del bello, del forte, del debole e del casuale sono valide. […]. Ma su cosa si basano queste categorie del bello e del non bello, del forte e del debole, eccetera? Ebbene, si basano sulla divisione delle orbite secondo i conoscibili, ovvero costruibili, poligoni regolari […] cioè sono relazioni armoniche primordiali previste nell'essere divino.

Ciò che risulta evidente è una vera rivoluzione di tipo scientifico:  indagare la Natura vuol dire rintracciare le relazioni geometriche che la descrivono. Una visione apparentemente quasi paranoica, ma che ha aperto veramente le porte alla Scienza moderna.

Analizzando la realtà sotto forma di forme e rapporti di pura armonia, le sue leggi ne derivano quasi automaticamente. Le orbite stanno dentro una sfera, ma l'importante è che la sfera sia abbastanza spessa da permettere al corpo celeste di muoversi su una traiettoria non più circolare (dogma fino ad allora assoluto). Ne nasce il legame con l'ellisse, con la velocità variabile e con la seconda legge. Il Sole diventa parte integrante di tutto ciò occupando uno dei fuochi, ergendosi a vero motore propulsore. Poi, infine, le distanze armonicamente e quantitativamente legate a rapporti musicali, ricordo degli assunti platonici, permettono di costruire la retta perfetta che lega distanze e tempi di percorrenza, ossia la terza e fondamentale legge che è uno dei capisaldi di tutta la dinamica del Cosmo.

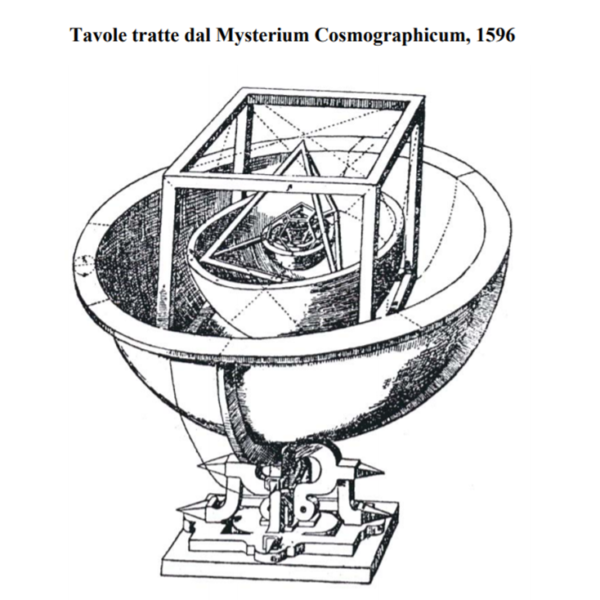
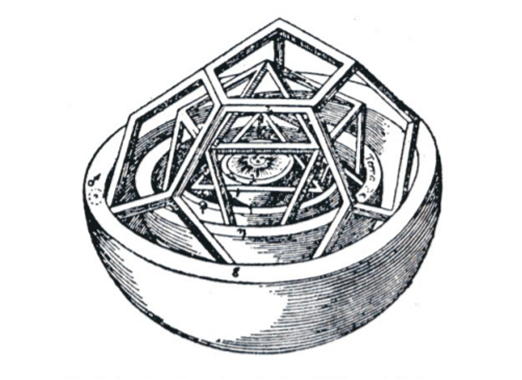
Non ridiamo quindi  nel vedere il modello fatto di sfere e di poliedri costruito da Keplero (Fig.re 6 e 7). Giudichiamolo, invece, come il punto di svolta da una Scienza ancorata ad assunti divini a una Scienza rigorosamente esprimibile in termini matematici e in leggi generali.

La Fig 8 che segue mostra la situazione con i valori dei "semiassi" e poi con i suoi quadrati:

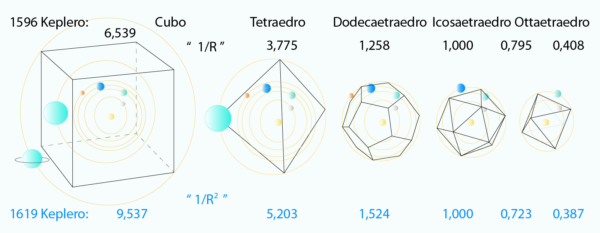
In qualche modo (perdonatemi...) potremmo paragonare Keplero a Einstein: la ricerca continua della perfezione (ottenuta grazie alla precisione delle misure di Tycho Brahe, suo grande maestro e oppositore) gli diede il coraggio di abbandonare qualsiasi teoria precedente, distruggendo con coraggio proprio gli assiomi di Platone e di tanti secoli successivi. Un coraggio e una fantasia che solo Einstein ha poi mostrato nell'abbandonare le leggi di Newton, pur giudicandole essenziali.

Risalta ancora una volta la frase di Feynman rivolta alla relatività generale: "... non mi stupisce la teoria in sé quanto il come abbia fatto a pensarci". Bene... la stessa cosa vale per Keplero: non stupisce la teoria finale (forse addirittura ovvia come un uovo di Colombo), ma il fatto che Keplero abbia  potuto pensare a orbite ellittiche e a velocità non uniformi, piazzando il Sole nell'unico punto che gli poteva competere. Dalla metafisica a una visione di impressionante realtà.

Quante cose si possono ancora imparare dagli antichi... la vera scuola non dovrebbe mai dimenticarlo. Argomenti  mai obsoleti, ma sempre pronti a dare capacità razionale e stimoli agli allievi.

So che questo articolo è, in qualche modo provocatorio e fuori dal pensiero comune, ma a volte prima di giudicare bisogna sapere e volere riflettere. Consideriamolo un tributo al grande Keplero!