Categorie: Relatività
Tags: Muone paradosso dei gemelli quiz relatività ristretta simmetria della RR sistemi di riferimento
Scritto da: Vincenzo Zappalà
Commenti:32
NEW: Se esiste il paradosso dei gemelli deve esistere il paradosso del muone (con soluzione molto personale)
Se è la prima volta che vi imbattete nel Paradosso dei Gemelli (o se ne avete già sentito parlare, ma volete rinfrescare la memoria) tutto quello che vi serve sapere per comprenderlo (e anche per "scherzarci" un po' su!), lo trovate QUI
Tentiamo di risolvere il paradosso dei gemelli (ancora lui!) senza fare tornare indietro l'astronave. Vi è differenza tra il viaggio del muone e quello dell'astronauta? Sembrerebbe di no, se il gemello "sedentario" fosse un po' particolare. Questa conclusione sembrerebbe portarci a distruggere completamente un paradosso che tale non è. Dove sbaglio?
Un modo apparentemente diverso per far coincidere il paradosso dei gemelli con la favola del muone e trarre conclusioni che renderebbero il paradosso dei gemelli un gioco da bambini. In particolare, un caso "normale" di relatività ristretta (?).
Cosa ci dice la favola del muone? In breve, dimostra che il muone che arriva dallo spazio vive di più del muone che nasce e muore sulla Terra. Questo non è certo un paradosso e l'abbiamo dimostrato con l'applicazione della relatività ristretta soltanto, dato che ne è un esempio perfetto. E lo dimostra anche la realtà dei fatti.
Vediamo, allora, cosa succede al nostro muone viaggiatore rispetto al muone sedentario. Ammettiamo che essi nascano nello stesso momento. E già qui si pone il primo problema. "Nello stesso momento" in quale sistema di riferimento? Dobbiamo dirlo, dato che sappiamo che la simultaneità dipende dal sistema di riferimento.
Bene, consideriamo quello della Terra. Possiamo allora rappresentare il tutto nel solito utilissimo diagramma di Minkowski.
Al tempo t = 0 (terrestre) nascono entrambi i muoni (mS e mT), ma uno nasce alla distanza d dalla Terra. Come questo nasce, però, raggiunge istantaneamente una velocità molto prossima a quella della luce, dirigendosi verso il pianeta. Il "fattaccio" è già stato compiuto, abbiamo perso la simultaneità degli eventi nei due sistemi di riferimento, ossia quello della Terra e quello del muone "spaziale".
Non preoccupiamocene, per adesso, e lasciamo terminare al muone il suo viaggio verso la Terra e verso il muone sedentario. Seguendo la relatività ristretta sappiamo benissimo che il tempo misurato dal suo orologio -e quindi dal suo "cuore"- passa più lentamente se osservato da Terra. Ne segue che, quando il muone viaggiatore arriva a Terra, il sistema di riferimento terrestre lo vede molto più giovane (nel tempo terrestre) del muone che è nato nello stesso momento (terrestre) ma è rimasto "fermo" nel sistema terrestre. La differenza di tempo è indicata dal segmento verde Δt nella Fig. 1.
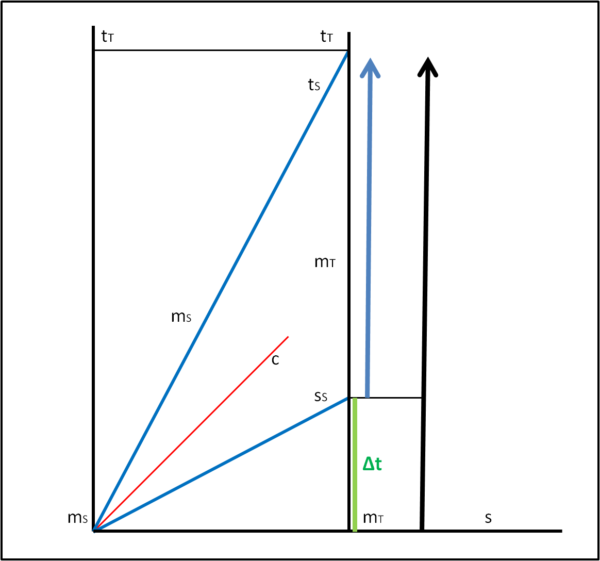
Attenzione: abbiamo detto arriva a Terra, ma non che si è fermato. Immaginiamo che imbocchi un tunnel speciale e che continui a viaggiare. Rimaniamo perfettamente nella relatività ristretta e chi è a terra VEDE il muone spaziale più giovane del muone terrestre. Tuttavia, la faccenda deve essere simmetrica e quindi basta invertire i due sistemi di riferimento (entrambi inerziali) per assistere al contrario: il muone spaziale che si considera fermo VEDE il muone terrestre più giovane di lui. Perfetto... ma allora perché il muone spaziale risulta veramente più giovane di quello terrestre (e gli esperimenti effettuati lo confermano)? Non introduciamo la contrazione della distanza, quella serve solo a dimostrare che alla fine del viaggio anche il muone spaziale concorda nell'essere il più giovane.
Pensiamo che il muone continui il suo viaggio. La relatività ristretta continua a essere seguita perfettamente e non possiamo rompere la simmetria: il muone mS DEVE vedere il muone terrestre più giovane di lui. Il vero problema è che Solo e che noi viviamo sulla Terra e ci interessa sapere quello che accade nel nostro sistema di riferimento. Facciamo quindi una SCELTA fondamentale: decidiamo di FERMARE improvvisamente il muone viaggiatore e confrontare il suo orologio (cuore) con quello del muone terrestre mT. Facendo questa azione, attraverso un rivelatore di muoni, BLOCCHIAMO, per così dire, il cuore del muone nell'istante in cui è stato trasferito dal suo sistema a quello terrestre. Il cuore perciò segna senza alcun dubbio il tempo trascorso, misurato nel sistema di riferimento del muone viaggiatore, e questo è decisamente più breve. Chi comanda il risultato è il sistema di riferimento in cui ci si mette.
Se, invece, facessimo un esperimento alquanto più difficile da realizzarsi, otterremmo esattamente il contrario, in pieno accordo col la RR: nel momento in cui il muone viaggiatore passa vicinissimo al muone terrestre, trasferiamo quest'ultimo, con qualche diavoleria tecnologica, nel sistema in moto del muone spaziale che continua a viaggiare con velocità costante. Se quest'ultimo muone avesse l'attrezzatura adatta concluderebbe senza ombra di dubbio che è il muone terrestre a essere più giovane di lui. Tutto ciò è più che normale per la relatività ristretta.
Qualche problema fino a questo punto? Tutto sembrerebbe tornare... chi si sente fermo (ossia nel sistema di riferimento che viene scelto) vede l'altro muone invecchiare più lentamente. La simmetria della RR è rispettata!
Dimostriamo, adesso che il paradosso dei gemelli può essere riportato esattamente a questo caso emblematico.
Basta solo e soltanto considerare un gemello GT "lontano", considerato gemello solo perché è nato nello stesso momento del gemello astronauta GS. Anche qui dobbiamo scegliere in quale sistema viene misurato lo stesso momento. Prima di nascere i due gemelli "speciali" stavano, in embrione, nello stesso sistema di riferimento, ossia in quello del gemello GS. Ancora una volta scegliamo il sistema del gemello (o muone) che chiamiamo sedentario GT, perché anche noi ci troviamo in quello.
Appena partito, l'astronauta GS cambia sistema di riferimento proprio come ha fatto il muone mS, e quando arriva all'incontro con il gemello sedentario, quest'ultimo lo VEDE più giovane di lui. In qualche modo, il gemello sedentario riesce a bloccare istantaneamente l'astronauta, senza farlo impattare violentemente (prodigi della tecnica!).
Bene, possiamo nuovamente concludere che l'astronauta, ormai inserito di nuovo nel sistema del gemello sedentario, è REALMENTE più giovane del suo gemello sedentario. Tutto perfettamente uguale al caso del muone. Siamo in relatività ristretta e non c'è bisogno di cambiare la Fig. 1, basta cambiare mT e mS in GT e GS.
Se, invece, fosse GT a venire trasferito improvvisamente nel sistema del viaggiatore GS, che ha deciso di non fermarsi, sarebbe il sedentario a essere realmente più giovane dell'astronauta. ESATTAMENTE COME E' CAPITATO AL MUONE.
Non appaiono differenze tra l'esempio del muone e quello dei due gemelli a ... distanza. Continuiamo a seguire perfettamente la simmetria della RR.
Bene, ora non ci resta che giocare un pochino col diagramma di Minkowski. Facciamo partire l'astronauta GS vicino al VERO fratello gemello G'T. Attenzione: poco importa la distanza iniziale tra i due gemelli, dato che il sistema di riferimento di GT è sempre lo stesso di GT, ossia i loro orologi da polso e quelli biologici girano sempre nello stesso modo, anche ad anni luce di distanza.
Appena giunto a metà percorso rispetto a GT (nel punto O), lo facciamo tornare indietro fino a tornare sulla Terra (Fig. 2), senza mai cambiare il modulo della sua velocità, ossia senza cambiare il fattore di Lorentz che vede la velocità al quadrato).
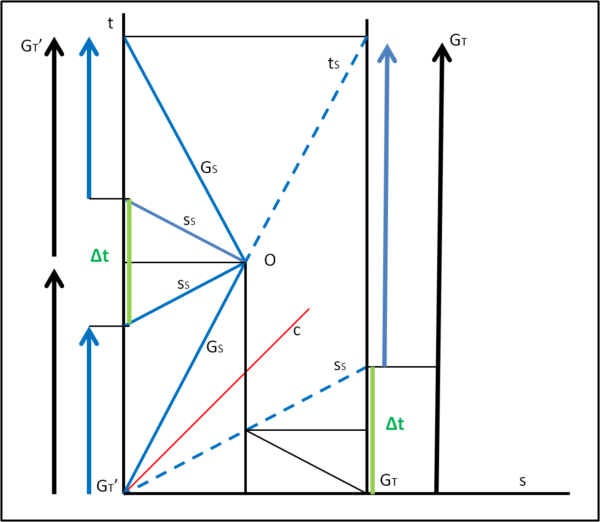
E' cambiato qualcosa nei tempi trascorsi dai due gemelli GT e G'T? Assolutamente no! L'astronauta arriva VIAGGIANDO vicino al suo vero fratello gemello G'T nello stesso tempo in cui era arrivato a incontrare il gemello lontano. Il gemello terrestre e il gemello lontano misurano lo stesso tempo ed entrambi DEVONO concludere che l'astronauta è più giovane di loro. Basta utilizzare qualche triangolo simile e la cosa risulta banalissima.
Cosa abbiamo dimostrato? Che, in fondo, ben poco è contato il cambiamento di percorso effettuato a metà del viaggio. Bastava considerare un gemello lontano e uguagliarlo a quello reale. Nuovamente, scegliendo di fermare il viaggiatore, quest'ultimo continua a risultare più giovane anche per il fratello gemello, avendo conservato il numero di battiti più rallentati del suo cuore, ossia la durata della vita trascorsa dalla partenza.
Arriviamo perciò a una specie di assurdo che tale non sembrerebbe: se il gemello reale sedentario si trasferisse sull'astronave in movimento costante del fratello astronauta sarebbe veramente il sedentario a essere più giovane. Ancora una volta la relatività ristretta avrebbe mantenuto la sua simmetria perfetta.
Il paradosso risulta tale solo perché si favorisce il sistema terrestre e si vuole fare tornare il gemello a casa. Lasciando libere tutte le possibilità non esiste assolutamente nessun paradosso.
QUIZ
Troppo "bello" per essere vero... dove sto sbagliando?
Un errore c'è e ciò comporterebbe il raggiungimento della velocità della luce, cosa impossibile!
P.S.: Ringrazio Massimiliano per avere solleticato lo sviluppo di questa "strana" favola e invito i più volenterosi a distruggermela o -almeno- a commentarla... malgrado il gran caldo!
Soluzione (molto personale).
Partiamo da un dato sicuro: il paradosso dei gemelli esiste veramente e il risultato che ci dice che il fratello viaggiatore rimane più giovane di quello sedentario è un dato di fatto. Quindi, il risultato che ho mostrato deve avere un baco. D'altra parte l'articolo su questo argomento affronta e risolve il problema in molti modi tutti perfettamente accettabili. Il ragionamento da me fatto è essenzialmente giusto fin quando consideriamo i due gemelli nati in luoghi diversi. Il loro incontro, come quello del muone con la Terra, rientra perfettamente nella RR. L'errore compare quando, lavorando sugli intervalli di tempo, concludo dicendo che vi è una perfetta simmetria tra il caso del gemello lontano e del gemello vicino.
Per scoprire il baco (in un modo secondo me convincente) basta mettersi nei panni dell'astronauta e vedere la situazione secondo il suo sistema di riferimento. Facendo così si dimostra che la simmetria va a rotoli. Infatti, assumiamo che l'asse del tempo verticale sia quello del viaggiatore dopo la partenza. Fino a metà percorso tutto resta all'interno della RR e vi è simmetria perfetta tra i punti di vista dei due sistemi di riferimento (quello del terrestre e quello del viaggiatore). A metà percorso, il viaggiatore decide di tornare indietro. E qui casca l'asino... Se vogliamo rappresentare questa manovra nel sistema di riferimento scelto all'inizio come "fermo", il nostro viaggiatore deve modificare la sua velocità. A questo punto prendo a prestito quanto detto prima della Fig.6 dell'articolo già menzionato, riguardo allo scambio dei segnali luminosi tra i due gemelli.
Cosa ci resta ancora da fare? Dimostrare che il fenomeno dell’invecchiamento UNIVOCO può essere confermato anche cambiando sistema di riferimento. In altre parole, il fenomeno deve rimanere lo stesso anche se si ci mette dal punto di vista dell’astronauta e si descrive il viaggio sotto questa nuova luce. Un esercizio molto utile per “pasticciare” nel nostro “amico” diagramma.
Imponiamo, perciò, come sistema di riferimento “fisso” quello dell’astronave alla sua partenza e vediamo a che soluzione si arriva. Il tutto è riportato in Fig. 6.
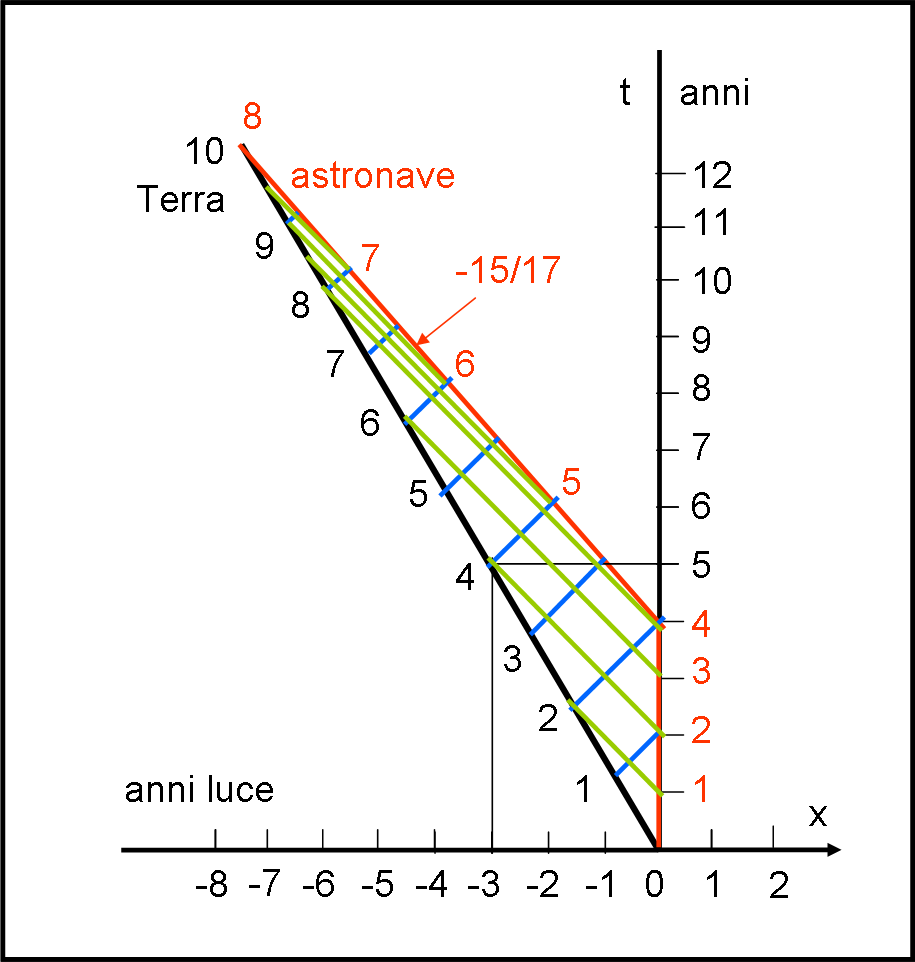
l’astronave, dopo 4 dei suoi anni "propri" cambia rotta e lascia il sistema di riferimento iniziale. Quale sarà la traiettoria descritta dall’astronauta rispetto alla linea di partenza? Beh… deve muoversi verso sinistra con velocità -v , ma non basta. In questo modo si muoverebbe parallelamente alla Terra e noi vogliamo, invece, che torni a casa! Per ottenerlo dobbiamo sommare un’altra velocità - v. Eccoci alla composizione relativistica delle velocità! Per ottenere la velocità con cui si muove l’astronave rispetto alla traiettoria iniziale è necessario applicare la formula della somma relativistica delle velocità.
u = (u’ + v)/(1 + u’v)
il che comporta una velocità finale, rispetto al sistema iniziale del viaggiatore che è ben diversa da - v, come mostrato nella figura precedente, tenendo ovviamente conto che i tempi propri devono restare sempre gli stessi. La simmetria va a rotoli e, in parole molto rozze, possiamo dire che quel poco che l'astronauta sembra perdere nel "breve" viaggio di andata, lo guadagna largamente quando decide di raggiungere la terra mantenendosi più giovane. Tuttavia, si è caduti nell'assurdo, perché la figura mostra tre sistemi di riferimento e non due come nel caso del muone o del gemello lontano.
Sicuramente ci sono molti modi per smontare un errore e chi ha risposto ha usato modi diversi. Insomma, non complichiamoci la vita inutilmente: il paradosso può essere risolto in tanti altri modi che comportano comunque solo e soltanto il fatto che se si cambia il sistema del viaggiatore si deve pensare di aggiungere un terzo incomodo e la differenza con il caso del muone diventa lampante.
Va bene, finiamola qui e non gettiamo maggiore confusione su chi pensava di aver capito (e aveva capito...). Chiedo scusa per essere stato proprio io a gettare confusione!






32 commenti
Quello che secondo me è sbagliato è considerare che venga rappresentata una linea spezzata nel diagramma spazio-tempo.
Consideriamo il gemello astronauta che deve percorrere una certa distanza fissa rispetto al sistema di riferimento terrestre, in questo caso le distanze si contraggono rispetto al gemello viaggiatore.
Se consideriamo l'astronauta fermo, il moto apparente della Terra è simmetrico rispetto a quello dell'astronauta e non avviene il fenomeno della dilatazione temporale (se consideriamo l'astronauta fermo infatti tutto l' Universo si muove rispetto ad esso, sarà per questo contratto e di questo ne ho parlato molto in vari commenti su questo blog "relativamente" al paradosso dei gemelli).
Tra moto dell'astronauta e moto apparente della Terra c'è simmetria, le distanze si contraggono allo stesso modo e non avviene il fenomeno della dilatazione temporale.
Il triangolo invece evidenzia un'altra situazione, ossia quello che succederebbe se fosse la Terra a spostarsi di una distanza che è fissa rispetto all'astronave ferma.
In quel caso il diagramma spazio-tempo è esatto, in quanto se la Terra si spostasse di una distanza fissa rispetto all'astronave il tempo di viaggio secondo i terrestri sarebbe ovviamente minore del tempo misurato dall'astronauta (le distanze in questo caso si contraggono rispetto ai terrestri e anche qui valgono le considerazioni fatte in precedenza relativamente al moto apparente che in questo caso è dell'astronauta)
Se il gemello terrestre (che ha viaggiato spostandosi di una distanza fissa rispetto al sistema di riferimento solidale con l'astronave) salisse alla fine in astronave continuerebbe ad essere più giovane del fratello.
Le trasformazioni di Lorentz sono simmetriche, questo è chiaro! Nessuno lo metterà mai in dubbio, Lorentz è Lorentz!
Invito tutti a riflettere quando all'inizio si considera il moto dell'astronauta che deve viaggiare per andare verso una posizione la cui distanza sia fissa rispetto al sistema di riferimento terrestre.
L'altra situazione di cui si discute è invece relativa al fatto che la Terra debba viaggiare per andare verso una posizione la cui distanza sia fissa rispetto al sistema di riferimento dell'astronauta.
Ciao Vincenzo, spero in futuro di riuscire a convincerti che la mia non è una "strana favola", un abbraccio!
Scusatemi, volevo completare il mio messaggio precedente nel sottolineare che i diagrammi spazio-tempo di Minkowski hanno la loro importanza e sono affascinanti (figuriamoci, è bellissimo lavorarci con le curve di calibrazione, all'Università era il mio passatempo preferito! I giovani magari borbotteranno ma Internet sì c'era ma era uscito da poco, costava e non ho mai provato a verificare se esistessero blog affascinanti come questo)
La mia obiezione ai diagrammi di Minkowski è solo dovuta al fatto che perdono il loro fascino se vogliamo rappresentare con uno di essi il moto dell'astronauta ed il moto apparente della Terra, in quel caso l'asse delle distanze e l'asse dei tempi coincidono. (e naturalmente il moto di un fotone sarà identico per entrambi)
Quando invece avviene il fenomeno della dilatazione temporale allora sì che sono preziosi.
Ci tengo a sottolineare che Lorentz è Lorentz e, d'altra parte, Minkowski è Minkowski.
Buona estate a tutti!
forse ho trovato il nocciolo della questione che salva il muone e nega l'andata e il ritorno mostrato in figura... sta diventando un quiz...
Quando ho detto che l'asse delle distanze e l'asse dei tempi coincidono mi riferivo al fatto che sono i due assi delle distanze a coincidere e i due assi dei tempi a coincidere (scusatemi, magari avevate capito ma non voglio che si crei ambiguità)
La soluzione, caro Massimiliano, è molto più semplice. Commetto un grave errore, ma è divertente trovarlo...
Ok Vincenzo, se però vuoi salvare il muone e l'andata e il ritorno come dici (perché sta diventando un meraviglioso quiz) intanto cercherò di non commentare più in futuro (sono solo desideroso di sapere che ne pensano altri, come ti ho detto è bello condividere le proprie opinioni ascoltando le altrui), però forse è meglio aspettare che rinfreschi un pò (in molti sono in vacanza e magari non parteciperebbero al dibattito).
Ripropongo a mia difesa (con il COPIA E INCOLLA e con qualche piccolissima variazione) il commento dove avevo svolto l'esercizio che avevo mostrato a Vincenzo. (in questo caso i due gemelli potrebbero essere due muoni, perché no?)
Immaginiamo che un gemello (inizialmente sulla Terra) arrivi ad una distanza di 17,32 anni-luce per poi tornare indietro.
Poniamo che la sua velocità all'andata ed al ritorno sia costante e pari a v = 0,866 c (una bella velocità, quasi il 90% della velocità della luce); ho scelto tale valore in modo che il fattore di Lorentz equivalga a 2.
Tra andata e ritorno, rispetto ad un terrestre, trascorrono 40 anni (20 per l'andata e 20 per il ritorno)
Quindi, per chi è rimasto sulla Terra, sono trascorsi 40 anni ed è stata percorsa una distanza doppia di 17,32 anni-luce (34,64 anni-luce)
Secondo l'astronauta, l'Universo è in movimento rispetto ad esso e si è perciò contratto. Essendo il fattore di Lorentz uguale a 2, ogni distanza è per lui la metà rispetto a come misurato sulla Terra.
Sempre rispetto al gemello in astronave, la Terra (che si è inizialmente allontanata per poi tornare indietro) non ha percorso tra andata e ritorno 34,64 anni-luce ma la metà di tale valore che ovviamente equivale a 17,32 anni-luce (essendo stato scelto il fattore di Lorentz uguale a 2 è chiaro che tale valore coincide con la distanza di andata rispetto ad un terrestre, ma si può scegliere un altro valore della velocità e operare con un fattore di Lorentz diverso)
Riassumendo, rispetto al gemello astronauta, la Terra tra andata e ritorno ha percorso (sempre alla velocità v = 0,866 c ) una distanza di 17,32 anni-luce e sono perciò trascorsi solo 20 anni.
Dov'è la simmetria? Sono due moti che di uguale hanno solo la velocità.
Per il gemello rimasto sulla Terra l'astronave ha percorso 34,64 anni-luce in 40 anni ,
per il gemello in astronave la Terra ha percorso 17,32 anni-luce in 20 anni .
Quando i due torneranno nella stessa posizione, il gemello rimasto sulla Terra sarà più vecchio rispetto all'altro e questo vale a prescindere se i gemelli cambieranno "sistema di riferimento".
Se l'astronave non si fermasse e se il gemello rimasto ad aspettare sulla Terra riuscisse in qualche modo a salire in astronave (cambiando sistema di riferimento) continuerebbe ad essere più vecchio dell'altro.
E' chiaro poi che, prima di invertire la rotta e quando si tornerà sulla Terra, occorrerà decelerare. E' ovvio lo stesso considerare che quando l'astronave parte e subito dopo aver cambiato rotta occorrerà accelerare, in questo caso per determinare i tempi di viaggio è un pò più complesso perché occorre risolvere qualche integrale (che potrebbe benissimo essere stimato), ma il problema non cambia più di tanto.
“Se, invece, facessimo un esperimento alquanto più difficile da realizzarsi, otterremmo esattamente il contrario, in pieno accordo col la RR: nel momento in cui il muone viaggiatore passa vicinissimo al muone terrestre, trasferiamo quest'ultimo, con qualche diavoleria tecnologica, nel sistema in moto del muone spaziale che continua a viaggiare con velocità costante. Se quest'ultimo muone avesse l'attrezzatura adatta concluderebbe senza ombra di dubbio che è il muone terrestre a essere più giovane di lui. Tutto ciò è più che normale per la relatività ristretta.”
Dieri che è una affermazione sbagliata.
Ci sono in generale fondamentalmente 2 errori.
Il deltaT non è un tempo assoluto, ma è per definizione la differenza tra 2 tempi t2-t1.
Se poi t1 è zero allora esiste la corrispondenza, ma è un caso specifico.
La dilatazione dei tempi non calcola un t, ma un deltaT che è una cosa diversa.
Per trovare il t finale serve sempre il tempo iniziale.
Tutto questo per arrivare a dire che la dilatazione dei tempi calcola lo scorrere del tempo, ma non ti dà il valore finale.
Se io dico che per una persona sono passati 10 anni, e non conosco il tempo inziale, non posso sapere quale sia la sua età finale.
La simmetria nella RR vale per il deltaT.
Se A e B sono in moto tra loro, A misura il tempo di B scorrere più lentamente del proprio, e B misura il tempo di A scorrere più lentamente del proprio, il tutto in accordo con la formula della dilatazione dei tempi.
Ma per sapere il tempo finale reale di A e B per poi confrontarli, devo sapere il loro tempo iniziale.
E qui arriva il secondo errore.
Il tempo iniziale dipende dal sistema di riferimento e segue la variazione di simultaneità tra i 2 sistemi, nel caso ci sia una variazione di velocità.
Per A e B può ad esempio scorrere lo stesso tempo deltaT, ma non è detto che il tempo finale sia lo stesso perché il tempo inziale può essere diverso.
Ovvero possiamo mantenere la simmetria tra lo scorrere del tempo di A e B (deltaT o dilatazione del tempo), ma comunque avere valori finali del tempo diversi a causa di una variazione di sistema di riferimento ovvero di simultaneità.
Il tutto per arrivare a questo caso.
A è sulla terra, B è lontano su un pianeta.
A e B hanno la stessa età, 20 anni.
B parte e torna a casa.
Quindi A non cambia sistema di riferimento, B invece sì.
Dal punto di vista di A.
A vede B muoversi nello spazio.
Dopo la partenza, B ha sempre 20 anni, ma il suo tempo scorre più lentamente rispetto ad A, quindi arriva sulla terra che è più giovane.
Ovvero se per A passano 10 anni(deltaT) e si ritrova ad avere 30 anni (deltaT più tempo iniziale), il tempo di B scorre più lentamente secondo la formula della dilatazione dei tempi, ovvero 8 anni e si ritrova ad avere 28 anni.
Quando B arriva sulla terra, ovvero coincide spazialmente con A, poco importa se si ferma (cambiamento di sistema di riferimento) o se continua il suo viaggio (nessun cambiamento di sistema di riferimento)
Come è irrilevante che A salti sull’astronave (cambiamento di sistema di riferimento).
Perché la variazione del sistema di riferimento fa cambiare la simultaneità, ovvero cambia l’angolo della retta, ma se siamo nello stesso punto il tempo percepito (la simultaneità) di A con B e B con A non cambia.
Concludendo
Quando A e B coincidono spazialmente, il primo ha 30 anni il secondo ne ha 28.
Dal punto di vista di B.
B vede A muoversi nello spazio, ma solo B ha cambiato sistema di riferimento.
Per B passano 8 anni, perché dal suo punto di vista la distanza con la terra si riduce, contrazione delle lunghezze, e arriva sulla terra (che si fermi o no) all’età di 28 anni.
Ma, subito dopo la partenza, dal punto di vista di B, si ha che A non ha più 20 anni.
Il punto è tutto qua, cambia la simultaneità tra B e A, perché B ha cambiato sistema di riferimento, quindi percepisce A avere un altro tempo.
Cambia la retta di simultaneità del sistema di B.
B misura, subito dopo la sua partenza, A avere 23,6 anni (tempo iniziale di A visto da B).
A fa un salto in avanti, magia?
Forse, ma è così, può non piacere, ma è così.
In realtà bisogna dire, che il salto è progressivo, perché non esiste una accelerazione istantanea.
Questo comporta una variazione continua dell’angolo della retta di simultaneità.
Oppure durante l’accelerazione, chi sta più in alto ha l’orologio che gira più velocemente…
Quindi se nel viaggio di B passano per lui 8 anni, dal suo punto di vista per A scorrono (deltaT) 6,4 anni.
Perfetta sintonia con la dilatazione dei tempi, e perfetta simmetria.
Quando B arriva sulla terra, che si fermi o no o che A salti sull’astronave, per A sono passati 6,4 anni (deltaT) più 23.6 anni come tempo inziale, si ha 30 anni.
Dal punto di vista di B, il tempo (deltaT) di A è passato più lentamente (totale simmetria), ma avendo un tempo inziale più alto (per il cambio di simultaneità), ne risulta che A è più vecchio.
Nessun paradosso e simmetria rispettata.
A me sembra tutto perfettamente logico e semplice.
In una delle volte precedenti che abbiamo affrontato questo (non)paradosso avevo provato a fare una figura per mettere in evidenza l'assimmetria dei due gemelli. La ripropongo sperando che possa essere utile per chiarire come il cambio di direzione più o meno repentino generi l'assimmetria tra i due gemelli.
Per descrivere il problema si può ancora utilizzare il sistema di riferimento del gemello stanziale che non subisce accelerazioni.
In questo sistema di riferimento la linea d'universo del gemello stanziale è l'asse verticale. La linea d'universo del gemello viaggiatore è invece composta da 5 tratte. Ci sono le due rette (nere) dei percorsi fatti a velocità costante nell'andata e nel ritorno. Queste due rette sono raccordate tra loro e con la linea d'universo dell'altro gemello con curve per i periodi nei quali è presente l'accelerazione alla partenza, all'arrivo e nella inversione di rotta. Queste curve sono iperboli se supponiamo l'accelerazione costante. Le linee verdi sono le linee di simultaneità di istanti equidistanti per il gemello viaggiatore. Il loro diradarsi sull'asse dei tempi del riferimento del gemello stanziale (asse verticale) evidenziano lo scorrere più lento del tempo di questo gemello in presenza dell'accelerazione quando visto nel sistema di riferimento del gemello stanziale, cioè con il tempo proprio del gemello stanziale.
Nel caso il cambio di direzione fosse repentino, l'effetto del rallentamento del tempo si concentrerebbe in un punto. Si manifesterebbe con un salto istantaneo della linea di simultaneità che farebbe corrispondere un istante del gemello viaggiatore ad un intervallo di tempo finito per il gemello stanziale.
Un diagramma analogo non può essere fatto scambiando i sistemi di riferimento dei due gemelli perchè non esiste un sistema di riferimento del gemello viaggiatore. Occorrono almeno due sistemi di riferimento inerziali per descrivere lo stesso fenomeno visto dal gemello viaggiatore.
Ohi... ohi...
Simone vuole dimostrare, se non sbaglio, che anche senza inversione di rotta non si ha simmetria (A resta sempre il più vecchio). Beh, questo non può essere vero dato che ognuno ha mantenuto il suo unico sistema di riferimento e ognuno vede l'altro più giovane. Spostandosi magicamente sull'altro sistema non cambia il suo tempo proprio che è sempre lo stesso. In un caso risulta più giovane A e in un caso B. Sempre che abbia capito bene cosa vuol dire Simone... Una figura ci starebbe bene.
Fabrizio tocca meglio il problema, secondo me. Soprattutto si avvicina alla mia deduzione (ma può non essere la migliore...), quando dice: "Un diagramma analogo non può essere fatto scambiando i sistemi di riferimento dei due gemelli perché non esiste un sistema di riferimento del gemello viaggiatore. Occorrono almeno due sistemi di riferimento inerziali per descrivere lo stesso fenomeno visto dal gemello viaggiatore."
Secondo me siamo ricaduti nel caso illustrato dal capitolo su "i due gemelli mantengono il contatto", Fig. 6, dell'articolo
http://www.infinitoteatrodelcosmo.it/2018/02/07/cio-avreste-voluto-sapere-quei-paradossali-gemelli/
Componendo due velocità bisogna ricordarsi la loro somma relativistica e ciao simmetria!
In poche parole, se non vi è cambiamento di rotta, ossia di sistema, i diagrammi di Minkowski fatti cambiando sistema "fisso" sono perfettamente simmetrici. Se, invece, costringo l'astronave a eseguire il cambio di rotta, questo cambio di rotta si traduce in un diagramma non più simmetrico con quello terreste. Fig. 5 e 6...
Bello, siamo in tanti!
Vorrei proporvi una domanda di cui saprò l'esatta risposta tra una settimana e questa volta i personaggi della storia non sono due gemelli, potrebbero comunque anche esserlo (e il problema non cambia), so solo che si chiamano Alfa e Beta (entrambi terrestri) e devono ancora tornare per raccontarci della loro esperienza.
Una settimana fa Beta è salito a bordo di un'astronave per un piccolo viaggio (alla velocità v = 0,866 c) , si è allontanato per poi riavvicinarsi e ben sapeva che quando sarebbe tornato in prossimità della Terra il suo tempo di viaggio (misurato secondo il sistema di riferimento dell'astronave) sarebbe durato 15 minuti , era comunque rimasto d'accordo con Alfa che avrebbe dovuto continuare a rimanere a bordo dell'astronave.
Siamo tutti d'accordo che per l'orologio di Alfa (rimasto sulla Terra) il viaggio è durato 30 minuti e così è stato.
L'esperimento che hanno voluto realizzare è questo: poiché Alfa ha avuto una mezz'ora di tempo di attesa ne doveva approfittare per farsi una doccia nei primi 20 minuti (non un minuto di più e non un minuto di meno), poi si è vestito e ha aspettato l'astronave su cui Beta è tornato. (puntualissima!)
Appena l'astronave è passata, Alfa è riuscito a salire a bordo e si è allontanato con lui (e su questo vi assicuro che sono in tanti a poterlo testimoniare). Torneranno tra una settimana e sicuramente chiederò a loro in futuro come è andato l'esperimento.
Scusatemi, stavo per inviare il commento, ma non vi ho detto che cosa dovevano effettivamente sperimentare.
Vogliono sapere se Alfa sia pulito e ben vestito una volta salito a bordo dell'astronave, se sia ancora insaponato e intento a lavarsi o se stia succedendo qualcos'altro, anche relativamente a Beta.
Vi chiedo gentilmente se sapete già come andrà a finire.
E siate sinceri perché da loro saprò tutto. (come vi ho detto, devo solo aspettare una settimana!)
Un altro quesito è per PapalScherzone (il grande Scherzy che mi sta aiutando nel preparare le prossime verifiche). Chiedo a lui perché vorrei parlare di un fotone e, a dire la verità, ne conosco molti tristissimi perché non riescono a salire a bordo di nessuna astronave (nessuna è veloce come loro purtroppo)
Vorrebbero tanto viaggiare in una di esse anche perché sanno che il sindacato dei gemelli (che si offrono volontari per i nostri esperimenti ideali) ha ottenuto che le astronavi debbano essere dotate di ogni confort. Giustamente qualche esperimento ideale dura anche anni ed ogni gemello in viaggio ha diritto ad una buona cucina (non viaggia da solo, oltre ad uno chef personale che prepara ogni tipo di prelibatezze ha anche compagni di viaggio con cui "ingannare" il tempo), inoltre in astronave ci sono piscine, campi di calcio, di tennis e camere confortevoli per il riposo.
Il quesito è questo: se un fotone viaggia fino ad arrivare ad una distanza di 20 anni-luce dalla Terra, come sarà per lui il moto apparente della Terra stessa?
Sappiamo che per noi il viaggio dura 20 anni e, anche se non viaggerà in astronave, si è portato con sé tantissime paste alla crema. Secondo te Scherzy, quante ne potrà mangiare?
Mi raccomando, se puoi, raccontaci una storia divertente!
Piano...piano Massimiliano...
Cerca di non intasare il blog. Se vuoi puoi pure prospettare i tuoi problemi, ma uno alla volta e -ti prego ardentemente- di accompagnarli a delle figure! Senza figure diventa tutto troppo confuso e -a volte- male interpretato.
Mi raccomando...
Scusami Scherzy, un'altra domanda. Il fotone durante il viaggio si è portato una torcia elettrica (lo so è strano!)
Se in viaggio mentre si allontana dalla Terra accende la torcia elettrica puntandola verso la Terra, con quale velocità noi terrestri vedremmo viaggiare i fotoni emessi dalla torcia?
Anche qui una storia divertente, grazie!
Ok, hai ragione ma le domande non avevano bisogno di figure e due erano solo per Scherzy!
Scusami.
E poi attento! Per un fotone il tempo passa normalmente... Siamo noi che vediamo il suo orologio sempre fermo! Occhio alla differenza tra tempo proprio e tempo improprio. Cerchiamo di non creare confusione, ti prego...
Il fotone mangia una pasta ogni minuto con il suo tempo proprio, ossia secondo il suo orologio, ma noi non lo vedremo mai mangiare!
Se tu intendi: quante paste mangerà secondo i nostri 20 anni, la risposta è nessuna. Se intendi secondo il suo orologio la risposta è una ogni minuto.
Come per il muone... la sua vita misurata con il suo orologio è lunga 2, per noi è molto più lunga, misurata con il nostro orologio. Un fotone ha per noi una vita infinita, dato che non riusciremo mai a vedere girare il suo orologio biologico. Non riusciremo mai a vedergli mangiare una pasta.
Se in viaggio mentre si allontana dalla Terra accende la torcia elettrica puntandola verso la Terra, con quale velocità noi terrestri vedremmo viaggiare i fotoni emessi dalla torcia?
Questa la so ! Noi terrestri vediamo viaggiare i fotoni della torcia alla velocità della luce, che è sempre costante e non si somma né si sottrae ad altre velocità, nemmeno a se stessa.
! Noi terrestri vediamo viaggiare i fotoni della torcia alla velocità della luce, che è sempre costante e non si somma né si sottrae ad altre velocità, nemmeno a se stessa.
Per il resto, caro Massimiliano, vorrei accontentarti all'istante, ma per quanto provi a correre velocemente, il mio tempo disponibile non si ancora è sufficientemente dilatato (sarà colpa dei chiletti di troppo... )
)
La relatività papalliana ancora non è stata scritta, ma, come si dice a PapalFirenze... di'cche c'è, 'un manca nulla! (trad: di tutto ciò che c'è nel blog, non manca niente!).
Infatti le storie divertenti ed istruttive in questo blog non mancano. Intanto puoi goderti quelle che ha scritto il mio amico Paolino Papallicolo: le trovi qui http://www.infinitoteatrodelcosmo.it/la-fisica-classica-papalla/ e qui http://www.infinitoteatrodelcosmo.it/tag/i-papalli-nel-mondo-subatomico/.
Se, poi, vuoi dare il tuo contributo, scrivi a infinitoteatrocosmo@gmail.com e ti garantisco che valuteremo seriamente ogni tua proposta. Perché qui si ride e si scherz(y)a, ma la relatività la prendiamo molto seriamente.
Ritornando alla domanda '.. dove sto sbagliando?', credo che lo 'sbaglio' sia nella affermazione "se il gemello sedentario si trasferisse....sarebbe il sedentario ad essere più giovane".
Questa affermazione non è vera. Le considerazioni fatte sulle età dei gemelli, o meglio sul tempo trascorso dalla partenza del primo gemello viaggiatore, rigurdano il tempo proprio del gemello sedentario e la somma dei tempi propri dei due gemelli viaggiatori. Questi valori non dipendono dal sistema di riferimento nel quale si opera. Sono valori calcolabili in ogni sistema di riferimento, sui quali tutti gli osservatori concordano.
Nella figura del mio precedente commento si vede che le tacche del tempo sono di meno per il/i gemello/i viggiatore/i che quello per il gemello sedentario.
E che dire, caro Massimiliano, delle storie divertenti scritte qui http://www.infinitoteatrodelcosmo.it/tag/astericcio/ dagli astericci??
Credo di averti dato abbastanza compiti per l'estate... leggi, studia... e poi a settembre ti interrogo
Caro Fabry,
temo che il problema in generale sia anche quello dell'interpretazione di certe frasi...
Il muone (classico) quando impatta contro il rilevatore terrestre è come se si trasferisse con il suo tempo proprio nel sistema terrestre. E questo tempo resta quello che è. In questo senso intendo il "trasferimento".
Quando il gemello viaggiatore torna sulla Terra, i battiti del suo cuore (tempo proprio) rimangono quelli che sono e quindi, nel "trasferimento" , è veramente più giovane. E' il solito problema del tempo improprio e di quello proprio... Misurato con l'orologio terrestre il tempo proprio del viaggiatore risulta un tempo improprio.
Non vorrei che si dicesse la stessa cosa, gettando, però, confusione nei lettori...
Forse è meglio lasciar perdere e non aggiungere altro. Che ne dici? Noi ci capiamo, ma non vorrei che facessimo un cattivo servizio per molti altri.
Grazie mille Scherzy e grazie a Vincenzo. Vorrei comunque che mi rispondiate alla storia di Alfa e Beta anche senza troppi calcoli e potete benissimo rispondere che il problema è mal posto, che Alfa si è fatto la doccia oppure no, che Beta è arrivato prima, dopo, insieme (quello che volete) e anche senza calcoli, magari i calcoli in futuro. È solo per vedere se ci intendiamo, poi Vincenzo se viene posto un problema devo indicare il tempo rispetto a chi altrimenti se non lo dico mi potresti rispondere che non l'ho detto. Lo so come si fa si sbaglia (prometto comunque che non parlerò più di tempo proprio perché su quello siamo d'accordo da ieri che è invariant e). Vi prego, fatemi sapere di Alfa e Beta, devo ancora aspettare una settimana e va a finire che non saranno in grado di dirmelo neancge loro (se tornano sulla Terra come hanno promesso)
“Simone vuole dimostrare, se non sbaglio, che anche senza inversione di rotta non si ha simmetria (A resta sempre il più vecchio).”
No, forse mi sono spiegato male.
Voglio dimostrare che anche senza inversione di rotta si ha la simmetria, ma A resta sempre più vecchio di B per entrambi i sistemi.
Il punto è che la simmetria si ha sul tempo trascorso (deltat), ovvero durante il viaggio, A misura l’orologio di B girare più lentamente, e B misura l’orologio di A girare più lentamente.
Ma alla fine sempre e solo uno resta più giovane, perché il tempo finale è dato dal tempo iniziale più il deltat e il tempo iniziale tra A e B è diverso dopo che è avvenuta l’accelerazione a causa del cambio di simultaneità.
In pratica si vorrebbe vedere la simmetria nell’età finale di A o B, ma è sbagliato.
Ovvero si vorrebbe vedere B più giovane di A, e simmetricamente A più giovane di B.
No, è il rallentamento del tempo dell’altra persona visto da se stessi che è simmetrico, questo è quello che dice la RR (dilatazione dei tempi con perfetta simmetria).
Poi il tempo finale, o l’età finale è data dalla somma del tempo trascorso con il tempo iniziale, e qui interviene la simultaneità.
In pratica ci sono 2 fattori da combinare: la dilatazione temporale e la simultaneità.
“Beh, questo non può essere vero dato che ognuno ha mantenuto il suo unico sistema di riferimento e ognuno vede l'altro più giovane.”
No, perché?
È qui l’errore.
Nell’esempio da me fatto, A resta sempre nel suo sistema di riferimento, ma B no.
Io ho detto:
A è sulla terra, B è lontano su un pianeta.
A e B hanno la stessa età, 20 anni.
B parte e torna a casa.
Ma quando B parte, accelera, ovvero cambia sistema di riferimento, e quindi cambia la simultaneità tra i due sistemi.
Un istante prima della partenza B vede A avere 20 anni, un istante dopo lo vede avere 23,6.
Guardando la tua figura 1, mt ha fatto un salto pari a deltat, segmento verde, dovuto alla retta di simultaneità Ss.
Sia A che B vedono l’altro andare al “rallentatore” (simmetria), ma quel deltat ti porta ad avere una età finale che non è più simmetrica.
Questa è una delle possibili soluzioni del paradosso dei gemelli.
Poi che si possa fare il percorso con andata e ritorno, cambia poco, raddoppia il tempo di viaggio, ma alla fine vi è sempre almeno un cambio di sistema di riferimento.
Io ho fatto questo esempio in risposta al tuo quesito inziale posto nell’articolo, che riporto:
“Vediamo, allora, cosa succede al nostro muone viaggiatore rispetto al muone sedentario. Ammettiamo che essi nascano nello stesso momento. E già qui si pone il primo problema. "Nello stesso momento" in quale sistema di riferimento? Dobbiamo dirlo, dato che sappiamo che la simultaneità dipende dal sistema di riferimento.Al tempo t = 0 (terrestre) nascono entrambi i muoni (mS e mT), ma uno nasce alla distanza d dalla Terra. Come questo nasce, però, raggiunge istantaneamente una velocità molto prossima a quella della luce, dirigendosi verso il pianeta. Il "fattaccio" è già stato compiuto, abbiamo perso la simultaneità degli eventi nei due sistemi di riferimento, ossia quello della Terra e quello del muone "spaziale".”
Lo hai già detto tu, occorre tenere conto della diversa simultaneità.
Il muone nasce e dopo istantaneamente accelera: è cambiato il suo sistema di riferimento e quindi gli eventi che prima erano simultanei ora non lo sono più.
Attenzione, qui ci può essere un problema di interpretazione e forse questo è il vero problema.
Il muone nasce, e dopo parte, io ho capito così.
Questo è riconducibile all’esempio di A e B che ho fatto nel commento precedente.
Simmetria sul tempo trascorso, ma età finali diverse.
Se tu invece stai dicendo che il muone nasce già accelerato, allora cambia tutto.
Tu stai dicendo che A è sulla terra, e B è sull’astronave in moto.
In un certo istante e a una certa distanza sia A che B hanno 20 anni.
Ovvio che non c’è nessun cambio di sistema di riferimento, ma…
È un confronto assurdo, perché sono comunque 2 sistemi diversi con una diversa percezione degli eventi.
Istante di chi? di A o B, non è lo stesso istante, visto dal proprio sistema di riferimento.
Oppure, l’astronave dovrà pur aver accelerato, o è nata magicamente in moto?
Se A e B sono gemelli con l’astronave in moto (ovvero simultanei, stessa età), sicuramente quando l’astronave è partita in un passato remoto, ovvero prima della partenza, non erano gemelli, ovvero simultanei.
Non possono essere sempre simultanei, allora addio alla RR.
Allora è inutile parlare del paradosso dei gemelli, se i gemelli non ci sono.
Possiamo sempre dire che nel viaggio, A vede B andare al rallentatore, e B vede A andare al rallentatore, ma l’età finale è sempre dato dal tempo trascorso più quello iniziale.
E quale è questo tempo inziale?
Non si sa, nel senso che dipende dagli eventi prima che l’astronave si sia messa in moto, quando, in questo caso, i gemelli non erano gemelli.
Quindi può essere che quando B passa per la terra, A veda B essere più giovane.
Ma attenzione, altro grave errore, se questo è vero allora anche B deve dire di essere più giovane di A.
Non ha importanza se A salta sull’astronave, quando A e B coincidono nello stesso punto spaziale devono descrivere la realtà nello stesso modo, altrimenti addio secondo postulato della RR, non esistono 2 realtà diverse.
Direi per ora basta, fa troppo caldo per ragionare…
E naturalmente grazie anche a Fabrizio e a Simone. Se volete potete anche considerare che l'astronave acceleri (quando parte e cambia rotta) e che deceleri prima di cambiare rotta e prima di tornare a Terra. Se il problema non ha soluzione potete benissimo dirlmelo, ho fatto di tutto per cercare di fare meno confusione possibile ma il caldo gioca brutti scherzi.
Nell'invitarvi tutti a riferirmi su Alfa e Beta che poi gemelli non sono e comunque a prescindere da come risponderete
Buona Domenica a tutti!
Simone... come ho detto a Fabrizio, stiamo dicendo cose simili in modo diverso. Ovviamente, essendo in RR, non considero nessuna accelerazione: un oggetto passa da v = 0 a v = V in un tempo 0. E, quindi, il muone o chi per lui si trova allo stesso tempo sia appena nato che già in moto con una velocità costante. Nello stesso momento, nel riferimento terrestre, nasce anche l'altro muone.
Massimiliano... abbi pazienza. Per il fotone ti abbiamo già risposto...
Certamente il tempo proprio di un riferimento diventa 'improrio' se misurato con l'orologio di un altro riferimento. Quello che intendo dire è che il tempo prorio di un riferimento è calcolabile in ogni altro riferimento (distanza relativistica tra i due eventi). Su questo calcolo tutti i riferimenti concordano. Per questo calcolo non basta l'orologio, serve anche il metro. Nel confronto fra le età, implicitamente è stato fatto questo calcolo, che rimane valido su ogni riferimento. Credo che la cosa importante sia che il tempo biologico corrisponda al tempo prorio. Quindi non dipende dal sistema di riferimento che lo valuta.
Inoltre un cambio di velocità istantaneo, essendo istantaneo, non cambia il tempo proprio di chi lo subisce.
Per questo è indifferente da quale parte avviene il salto.
Sì aspetterò, potete benissimo parlare ancora d'altro, mi interessa lo stesso!
Caro Max,
dovresti spiegarti meglio su alfa e beta. Fanno tutti e due la doccia? Quanto dura la doccia in tempo proprio?
Forse questo quiz risponde alla tua domanda, almeno in parte
http://www.infinitoteatrodelcosmo.it/2018/12/02/minkowski-tutti-3-supernova-imprevista/
Veramente solo Alfa fa la doccia, però volendo anche Beta potrebbe farsela. Lì sono indicati i tempi o rispetto alla Terra o rispetto all'astronave e, appunto per '' calibrarci'' tra di noi vorrei sapere se in questo modo riesci a determinare il tempo proprio considerando la Terra come origine del sistema di riferimento Terrestre e considerando l' astronave come origine del sistema di riferimento dell'astronave. Sembra che il problema di Alfa e Beta non abbia nulla a che fare con il paradosso dei muoni viaggiatori ma, secondo me, a seconda di come risponderemo potremmo capire come noi interpretiamo personalmente il salto da un sistema di riferimento all'altro che possiamo anche considerare pensando che l'astronave acceleri o deceleri per passare da un sistema di riferimento all'altro. Leggendo i commenti di tutti noi ho infatti capito che iniziamo a considerare giuste le opinioni altrui e poi, stranamente, ci accorgiamo che gli altri stiano sbagliando e forse perché non ci capiamo quando affermiamo che non vale la simmetria (ad esempio) Fammi inoltre sapere se il tempo proprio di una doccia non è secondo te calcolabile e se quindi il problema di Alfa è Beta non ha senso. Se ci mettiamo d'accordo tutti su cosa intendiamo per simmetria, che cosa intendiamo per tempo proprio e inoltre per salto (anche non immediato) tra un sistema di riferimento all'altro potremo poi senza ambiguità passare nuovamente al problema dei muoni viaggiatori.
caro Max,
ti prego di non continuare a questo ritmo... sto preparando altre cose. Cerco di risponderti al volo, poi però lasciami andare avanti con altri argomenti.
Il tempo di alfa è tempo terrestre e tu m i dici che sono trascorsi trenta minuti tra la partenza e l'arrivo di Beta. Bene, non vedo problemi... E' come il paradosso dei gemelli. Alfa ha veramente avuto 30 minuti di tempo e non ha problemi a farsi trovare lindo e pulito. Poco importa a lui che quando arrivi beta gli sembri più giovane di 15 minuti rispetto a lui. Avendo fatto il percorso "chiuso" è caduto nel paradosso e quindi beta è veramente più giovane anche per lui stesso. Lasciamo perdere le divagazioni più o meno assurde e confermiamo chiaramente il risultato: beta cambia sistema tra andata e ritorno e quindi non può seguire le leggi della RR. Ed è inutile parlare di accelerazioni...
Vincenzo, purtroppo continuo a constatare che traspare una certa antipatia nei miei confronti, così come è stato in altri messaggi precedenti. Sei stato tu a chiedermi chiarimenti relativamente ad Alfa e Beta, avresti poi risposto un altro giorno. E quando ho detto che è possibile considerare che l'astronave acceleri e deceleri è perché a qualcuno non piace l'idea che si cambi velocità istantaneamente.
Tu invece mi hai detto che ho introdotto delle divagazioni assurde, ritenendomi in un certo senso uno sprovveduto.
D'altra parte, per quanto riguarda come si muove la Terra rispetto ad un fotone in viaggio, la risposta è che non si muove per niente ed un fotone in viaggio non avrebbe tempo di accendere una torcia elettrica.
Ti saluto definitivamente.
no, caro Massimiliano, nessuna antipatia, ma solo problemi di tempo a disposizione e ... non mi piace lasciare domande in sospeso... E poi devi ammettere che ciò che scrivi (senza alcuna figura) non è facile da interpretare correttamente ... le figure le puoi sempre mandare a Scherzy che le pubblica velocemente nei commenti.