Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica.

 

Un simpatico fenomeno di fisica classica  (facilmente riproducibile "praticamente") che porta a un risultato a prima vista sorprendente... Oltretutto, ci permette di ricordare alcune grandezze fondamentali e le loro relazioni. I due asterischi valgono per chi conosce già le basi della meccanica, altrimenti è meglio andarle a studiare nell'archivio... o nel libro "La Fisica Addormentata nel Bosco".

Cos'è l'impulso?

Siamo in un campo da golf e la pallina è sistemata sul suo appoggio, perfettamente ferma. Un giocatore a caso, ad esempio il nostro Frank, si accinge a colpirla. Se tutto viene fatto a regola d'arte, la mazza viene a contatto con la pallina per un tempo brevissimo, sicuramente molto più corto del tempo che la pallina impiega a fermarsi nuovamente. E' indubbio, comunque, che la pallina abbia acquistato velocità, partendo da ferma, ossia sia stata soggetta a un forza applicatale per un tempo che possiamo chiamare dt. La velocità è passata da zero a un certo valore v e quindi ha subito una variazione pari a dv.

Scriviamo la seconda legge della dinamica...

F = m a     (dove m è la massa della pallina che subisce l'accelerazione)

Possiamo anche scriverla:

F = m dv/dt

Ma la massa è una costante (siamo in fisica classica), per cui possiamo inserirla all'interno del differenziale dv...

F = d(mv)/dt

Cosa abbiamo scritto?

Abbiamo scritto che la forza è uguale alla variazione della quantità di moto rispetto al tempo.

Possiamo anche scriverla come:

F dt = d(mv)

E chiamare la prima parte a sinistra impulso, ossia assumere questa nuova grandezza vettoriale come una forza moltiplicata per il tempo in cui agisce. La forza potrebbe anche variare in questo piccolo intervallo di tempo, ma noi possiamo considerarla costante per i nostri scopi.

Ne segue un'interessante constatazione: l'impulso è uguale alla variazione della quantità di moto a seguito dell'applicazione brevissima di una forza costante.

i = d(mv)

Dato che immaginiamo che la pallina sia ferma al tempo t = o, possiamo scrivere che:

i = F(t - 0) = v m - 0 m = vm

In poche parole, sotto queste ipotesi, l'impulso non è altri che la quantità di moto posseduta dalla pallina.

Trattare le forze come forze impulsive è molto utile in tutti quei casi in cui la forza agisce per tempi brevissimi, come calciare un pallone, colpire una pallina da tennis, urtare contro qualcosa, ecc., ecc.

Ma, tra questi casi, ve n'è uno particolarmente interessante che abbiamo visto o causato chissà quante volte: far cadere una matita che è stata messa in verticale sopra un tavolo. Parlo di matita, ma potrebbe essere qualsiasi bacchetta rigida messa in equilibrio sopra una superficie piana.

Vogliamo vedere quale configurazione ci permette di fare toccare lo spigolo del tavolo alla punta della matita? Forza e coraggio... chi vuol provare da solo è liberissimo di farlo, anche perché ci sono sicuramente vari modi per ottenere il risultato. In poche parole, ci chiediamo: qual è la configurazione finale e da quali grandezze dipende?

Attenzione! A seconda dell'impulso che diamo la matita può cadere sia sopra il tavolo che andare a finire sul pavimento. Noi vogliamo descrivere il caso in cui la punta della matita tocchi esattamente lo spigolo del tavolo.

 

Una matita su un tavolo

In Fig. 1 usiamo proprio la matita e, con un po' di pazienza, la mettiamo in verticale. Per comodità, immaginiamo anche che la matita sia a base quadrata (non cambierebbe niente se fosse a base circolare, ma ci elimina l'uso del solito pi greco...). Cosa succede se diamo un colpetto alla base della matita? Sicuramente vediamo che la matita perde l'equilibrio e cade sul tavolo. Beh... un esperimento che sembra proprio inutile e banale...

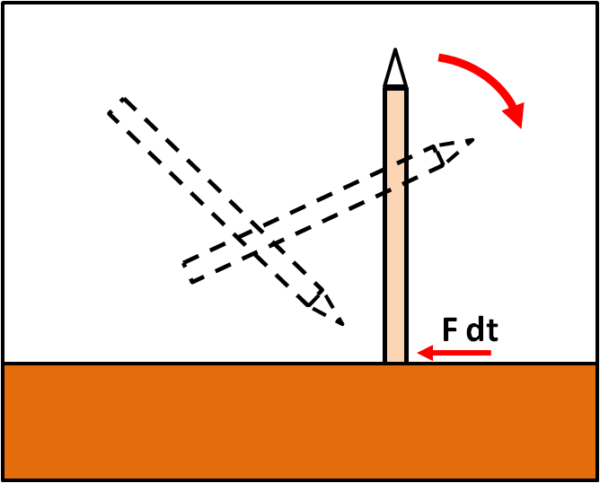
Un momento, un  momento... senza accorgercene abbiamo descritto un movimento non così banale... abbiamo, infatti, impartito un momento angolare alla matita (la stiamo facendo ruotare attorno al centro di massa) mentre quest'ultimo si muove di moto rettilineo uniforme con velocità v, lungo la perpendicolare all'asse iniziale della matita (la componente verticale del suo moto è quella che fa cadere la matita e non la tiene sospesa per aria...).

In fondo è quello che capita a un pianeta che gira intorno al Sole. Il pianeta subisce sia la rotazione attorno al Sole, ma anche lo spostamento rettilineo del Sole attorno al centro della galassia (abbiamo fatto coincidere il centro del Sole con il centro di massa del sistema pianeta  più Sole).

In parole povere la matita è soggetta a due movimenti: quello traslatorio con velocità v e quello rotatorio attorno al proprio baricentro, oltre alla caduta verso il basso.  I due moti devono combinarsi per potere spiegare compiutamente le configurazioni assunte dalla matita dopo che ha subito l'impulso iniziale. Cosa fondamentale è che la rotazione e la traslazione non sono indipendenti tra loro.

 

Spostiamo la matita sul bordo

Cerchiamo di rendere l'esperimento ancora più interessante e mettiamo  la nostra matita, in equilibrio, sul bordo del tavolo, come mostra la Fig. 2.

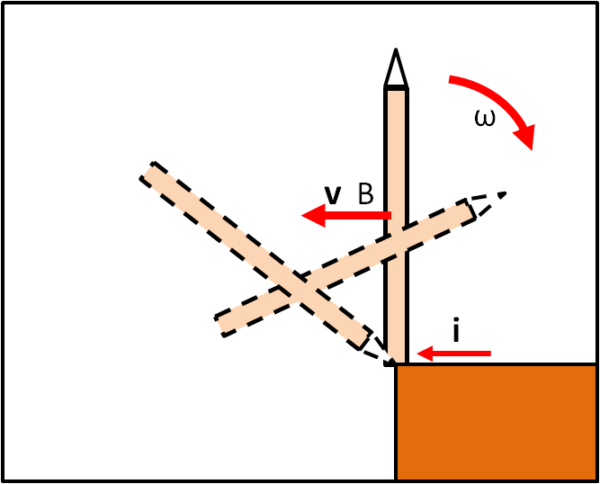
A questo punto diamo il solito colpetto alla base e... cosa succede? La punta della matita può toccare lo spigolo del tavolo?

Per saperlo, dobbiamo trovare la soluzione limite, ossia la configurazione in cui durante il suo moto roto-traslatorio, la punta della matita vada a toccare esattamente la punta del tavolo.

Ovviamente, la possibilità di toccare il tavolo esattamente con la punta è una configurazione che dipende essenzialmente dall'impulso che abbiamo dato alla matita o, in altre parole, alla velocità che abbiamo impresso all'estremità inferiore della matita. Tuttavia, a noi interessa vedere come questa configurazione limite possa essere raggiunta e da quali grandezze dipenda.

Ovviamente, c'è più di un metodo per ottenere il risultato, ma quello che utilizziamo è sicuramente molto elegante e ci permette di "rinfrescare" la memoria su alcune grandezze fondamentali della fisica classica.

 

Un momento...

Cominciamo a scrivere il momento angolare.

Ricordiamo che esso è il momento della quantità di moto, ossia è il prodotto vettoriale tra la quantità di moto e la distanza tra il punto di applicazione e il baricentro (nel nostro caso). In realtà la nostra quantità di moto è perpendicolare al vettore posizione e quindi possiamo tranquillamente considerare il modulo del momento angolare senza aver paura del seno dell'angolo (che vale 1).

Assumendo che la matita sia lunga 2a, a è la distanza tra base e centro di massa. Il modulo del momento angolare (momento della quantità di moto) è dato da:

L = m v a = i a           .... (1)

Il momento angolare è quindi il prodotto tra la distanza rispetto al baricentro e l'impulso.

 

Ancora un momento ...

Tuttavia, il momento angolare può anche essere determinato in altro modo. Invece di considerare l'inezia a muoversi (m), possiamo considerare l'inerzia a ruotare, che abbiamo chiamato momento d'inerzia. In tal caso, avevamo trovato che:

L = I ω                         .... (2)

dove I è il momento d'inerzia e ω la velocità angolare.

 

Esercizio facoltativo

Quanto vale il momento d'inerzia rispetto al baricentro? Potremmo trovarlo in moltissimi siti del web, ma possiamo anche permetterci di calcolarlo utilizzando un integrale estremamente facile. Ricordiamo la definizione di momento d'inerzia di un punto che dista r dal punto di riferimento:

I = m r²

Come ben sappiamo da ballerine che ruotano sul ghiaccio o da pulsar che ruotano, il momento d'inerzia, ossia l'inerzia alla rotazione, cresce con la distanza.

Nel nostro caso non abbiamo un punto, ma un insieme di punti che formano un corpo solido. Beh... basta dividere il nostro corpo (la nostra matita) in tanti volumetti piccoli piccoli e fare la somma di tutti i loro momenti d'inerzia. Fare una somma di elementi molto piccoli che tendono a zero vuole anche dire fare un'integrale con la distanza che va da 0 a r.

Prendiamo la nostra matita, ipotizziamola a base quadrata per semplificare le formule (non cambia assolutamente niente) e sezioniamola in tanti pezzetti piccoli piccoli di altezza dr e di base S. Sia ρ la densità del materiale, abbiamo che ogni volumetto dV moltiplicato per la densità ci regala la massa m del pezzetto considerato.

dm = ρ dV

Ma ogni volumetto è dato da:

dV = S dr

dm =  ρ S dr

Bene, a questo punto possiamo sommare tutti i momenti d'inerzia e trovare quello complessivo:

I = ∫₀^r ρ S r² dr

In realtà, avendo preso il baricentro come punto rispetto a cui dobbiamo calcolare il momento d'inerzia, dobbiamo calcolare sia quello tra o e r sia quello tra o e -r. Ossia fare la somma tra - r e r che, passando alla matita, diventa tra a  e - a.

I = ∫_-a^aρ S r² dr = ρ S [r³/3 ] _-a^a = ρ S 2a³/3 = (m/V)(2Sa³/3) = 2mS a³/(3 V) = 2m S a³/(3 2a S)

I = 1/3 (m a²)

 

La massa non serve

Non ci resta che inserire il risultato dell'esercizio nella formula del momento angolare, ossia nella (2) e abbiamo:

L = I ω = 1/3 (ma²) ω             ... (3)

Bene abbiamo trovato due equazioni ((1) e (3)) che ci forniscono il momento angolare e possiamo uguagliarle:

ia = 1/3 (ma²) ω

Ma sappiamo anche che l'impulso i vale proprio mv

mv a = 1/3 (ma²) ω

semplificando:

v = 1/3 a ω            .... (4)

Questo risultato può sorprendere a prima vista: la velocità di traslazione è legata alla velocità angolare senza che intervenga la massa. In altre parole la massa della matita può essere qualsiasi, ma il movimento non cambia!

 

La configurazione limite

Portiamoci, allora, nella configurazione limite che ci siamo prefissi: la punta della matita riesce a toccare il tavolo. La situazione è quella della Fig. 3.

 

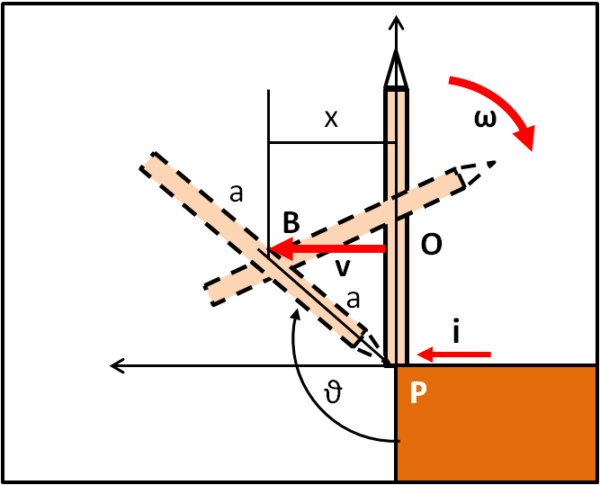
Cosa possiamo dire? Beh... che il baricentro della matita si è spostato di un certo valore x rispetto alla verticale di partenza e che la punta della matita ha descritto un certo angolo θ. La posizione assunta ci mostra un bel triangolo rettangolo con vertice nella punta della matita... In altre parole abbiamo che

x = a sin (180 - θ) = a sin θ

 

Sparisce anche la lunghezza

Sappiamo che:

v = (1/3) a ω

moltiplichiamo ambo i membri per t

vt  = 1/3 a ω t

ma

vt = x

e, ricordando il valore di x:

a sin θ   = (1/3) a ω t

Sappiamo, però, che la velocità angolare è data da:

ω = θ/t

e quindi:

a sin θ= 1/3 a θ

Semplifichiamo e abbiamo un'equazione in cui compare solo l'angolo e il suo seno:

sin θ = 1/3 θ            .... (5)

Altro risultato sorprendente: la configurazione finale è indipendente anche dalla lunghezza della matita!

Non ci resta che calcolare l'angolo θ (espresso ovviamente in radianti).

 

Una soluzione grafica

L'equazione (5) non è certo facile da risolvere, comparendo un funzione trigonometrica e un angolo. Potremmo usare qualsiasi programma della rete che ci fornisca il risultato. Non illudiamoci, però... quel risultato sarebbe sempre qualcosa di approssimato dato che è necessario troncare una serie (scrivere il seno in funzione dell'angolo...). Tanto vale farne a meno e rivolgerci a un semplice grafico.

I valori che soddisfano la (5) si possono trovare come intersezione delle due funzioni

y = sin  θ

e

y = (1/3) θ

entrambe facilissime da disegnare, come mostrato in Fig. 4.

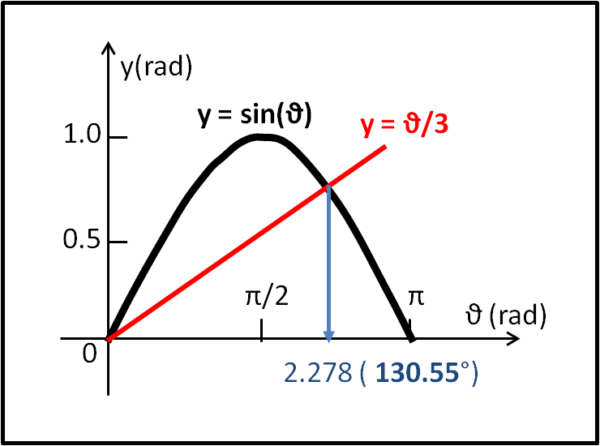
Tralasciamo, ovviamente, la soluzione più immediata, ossia quella relativa a θ = 0 (la matita non si muoverebbe...).

Molto più interessante è quella che deve trovarsi tra π/2 e π. A occhio sembra proprio a metà strada... Non ci resta che andare per tentativi in un intorno di 3π/4. Ovviamente, θ va espresso in radianti per confrontarlo con un seno.

Proviamo proprio per θ = 135°

sin 135° = 0.707

135/3 (in radianti) = 0.785

Dobbiamo diminuire l'angolo...

proviamo con 130°

sin 130° = 0. 766

130/3 = 0.756

Molto meglio, ma adesso è troppo piccolo... aumentiamolo di un grado

sin 131° = 0.755

131/3 = 0.762

troppo grande, un po' di meno...

sin 130.5 = 0.760

130.5 = 0.759

un pochino  di più

sin 130.6 = 0.759

130.6/3 = 0.760

Può bastare e concludere che l'angolo descritto dalla matita, per toccare esattamente il bordo del tavolo, deve essere uguale a 130.55 circa, qualsiasi sia la massa e la lunghezza della matita!

Ovvio? Forse sì, ma è un risultato intrigante e un bel... ripasso.

 

N.B.: non dobbiamo stupirci se non abbiamo fatto entrare in gioco la forza di gravità. Volendo trovare la soluzione limite abbiamo automaticamente trovato che il baricentro scende rispetto alla posizione verticale che aveva all'inizio. In pratica, questo vuol dire che è stata considerata la forza peso. Tuttavia, la componente verticale, può benissimo essere trascurata, dato che nel moto parabolico la componente  orizzontale della velocità rimane costante ed è proprio lei che ci permette di ricavare l'angolo. Inoltre, che la massa sparisca è già prevedibile pensando che la caduta libera di un grave è indipendente dalla massa. Meno prevedibile che sparisca anche quella "portata" dietro dal momento d'inerzia.