Categorie: Matematica
Tags: 45 gradi assi cartesiani geometria quiz rimbalzi soluzione y = x
Scritto da: Vincenzo Zappalà
Commenti:2
Soluzione del tiro eccezionale *
Nessuna risposta a un quiz molto facile (troppo facile?)... In ogni modo, noi la diamo lo stesso...
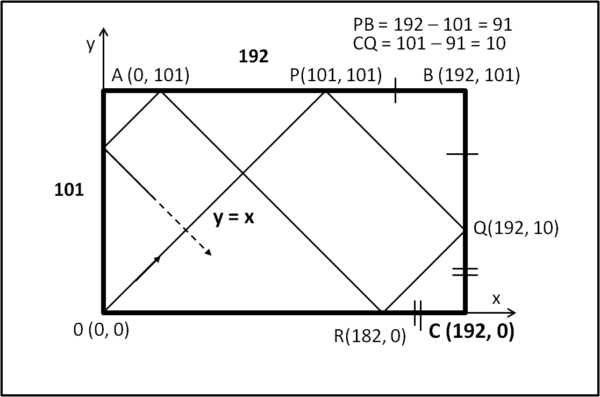
La soluzione è praticamente scritta nelle dimensioni del tavolo. Disegniamo nuovamente il nostro tavolo da biliardo, inserendolo in un sistema di assi cartesiano x e y, in cui y segue il lato corto e x il lato lungo. O sia l'origine degli assi e anche la posizione della palla al momento del tiro iniziale.
I quattro vertici del tavolo hanno quindi coordinate:
O (0.0)
A (0, 101)
B (192, 101)
C (192, 0)
Ricordiamo cosa significa effettuare un tiro a 45° rispetto agli assi: tracciare la retta y = x.
Il che vuol dire che i soli punti che la retta può incontrare sono quelli che hanno l'ordinata uguale all'ascissa. Se l'ascissa è pari lo deve anche essere l'ordinata; se l'ascissa è dispari lo deve essere anche l'ordinata. Dopo qualsiasi rimbalzo si effettui sulle sponde, la traiettoria continua a essere una eretta inclinata di 45° rispetto agli assi, anche se cambia l'origine e la direzione. Ne segue che le coordinate dei punti successivi devono mantenersi o entrambi pari o entrambi dispari (come mostrato per i primi punti P, Q e R). E' solo una questione di triangoli isosceli...
Ne segue che poco importa quanti rimbalzi faccia sulle sponde, ma la palla può solo toccare i punti del tavolo che abbiano come ascissa e ordinata due numeri pari o due numeri dispari.
L'unico vertice, a parte l'origine, che abbia entrambe le coordinate pari è solo e soltanto il punto C. Questo sarà perciò l'unico punto che potrà toccare la palla nel suo viaggio, per lungo che sia...
Tiralà, quindi, è sicurissimo del vertice che colpirà la sua palla, dato che i suoi tiri sono perfetti e la forza per far girare la palla anche per ore e ore la possiede. E' o non è il più bravo del mondo?
Il quiz lo trovate QUI






2 commenti
ZERO è un numero pari !
certamente... sono detti pari tutti i numeri che sono multipli di 2 e quindi dato che 0 x 2 = 0, anche lo zero è un multiplo di 2.