Categorie: Fisica classica
Tags: accelerazione centripeta moto circolare uniforme quiz
Scritto da: Vincenzo Zappalà
Commenti:2
SOLUZIONE del quiz sulla meccanica papalliana **
Risolviamo il problema usando solamente i vettori e le loro componenti secondo i due versori i e j relativi agli assi x e y. Utilizziamo sempre la Fig. 1.
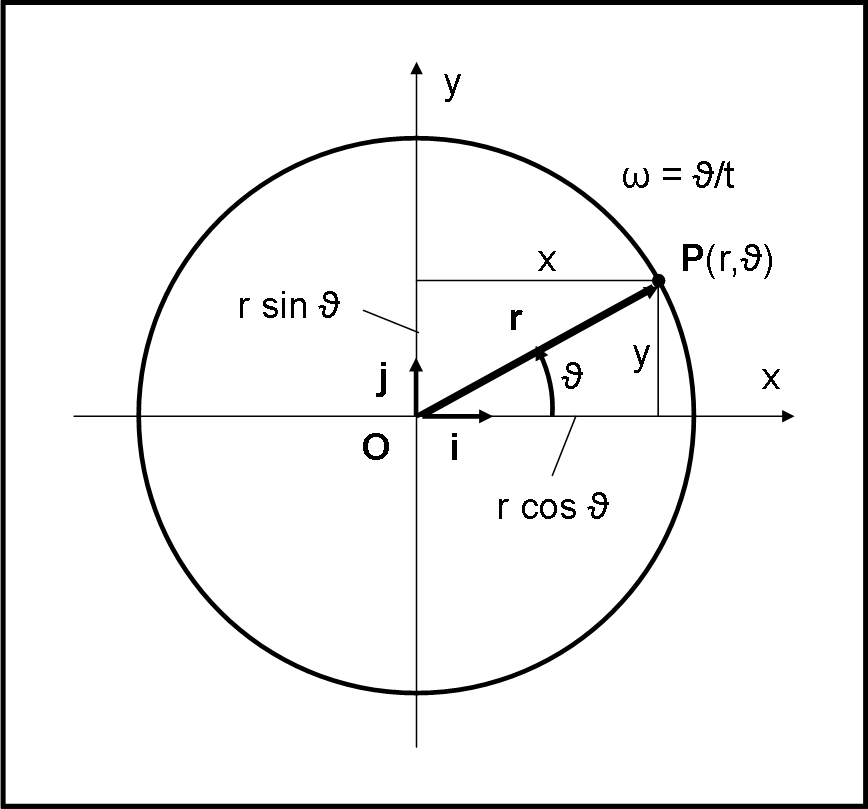
Dato il punto P di coordinate polari (r,ϑ), possiamo subito scrivere le relazioni tra (x,y) e (r, ϑ), ossia:
x = r cos ϑ = r cos ωt
y = r sin ϑ = r sin ωt
e, di conseguenza il vettore r che identifica la posizione di P rispetto a O:
r = xi + yj = (r cos ωt) i + (r sin ωt) j …. (1)
La velocità di P è data dalla derivata del vettore r rispetto al tempo, ossia
v = dr/dt = - ω (r sin ωt) i + ω (r cos ωt) j .... (2)
Per avere il suo modulo, basta applicare il teorema di Pitagora alle sue due componenti secondo gli assi ortogonali x e y:
v = (ω2r2 sin2ωt + ω2r2 cos2ωt)1/2 = (ω2r2(sin2ωt + cos2ωt))1/2 = (ω2r2)1/2 = ωr .... (3)
(Potevamo anche usare triangoli simili...)
Eseguiamo, adesso, il prodotto scalare tra r e v (ricordiamo che i x j = 0 e i x i = j x j = 1)
r x v = - (r cos ωt) (ωr sin ωt) + (r sin ωt) (ωr cos ωt) = 0 .... (4)
Se il prodotto scalare è nullo (e nessuno dei due vettori è nullo), i due vettori devono essere perpendicolari!
Per trovare l’accelerazione di P, basta fare la derivata della velocità rispetto al tempo:
a = dv/dt = - (ω2r cos ωt) i – (ω2r sin ωt) j = - ω2 ((r cos ωt) i) + (r sin ωt) j)
Ma, la (1) ci dice che:
(r cos ωt) i + (r sin ωt) j = r
E, quindi:
a = - ω2 r .... (5)
Il vettore è quindi diretto come r, ma di verso opposto. Il suo modulo è, ovviamente:
a = ω2 r
NB: le varie grandezze potevano essere calcolate con altri metodi anche più immediati, ma lo scopo del quiz era di utilizzare i vettori e le coordinate polari.






2 commenti
... e così, mentre io sudavo le proverbiali sette camicie (puff ... pant ... pant ... puff ), il buon Enzo, con due o tre pennellate d'artista risolveva il busillis.
), il buon Enzo, con due o tre pennellate d'artista risolveva il busillis.
Eeeeeeeeeeeh , d'altronde la classe non è acqua!
ma va là Alvy! Sei stato bravissimo e si poteva anche fare prima se non mi fossi incaponito con i vettori e le loro operazioni (si capisce che adoro i vettori e i loro figlioletti versori?)