Questo articolo è stato inserito nella sezione d'archivio "Sezione Aurea, spirale di Fibonacci e altre forme ricorrenti nell'Universo"

 

Questo articolo riguarda una delle forme più amate dalla Natura, l'esagono. Ci porta quasi automaticamente a una delle domande più intriganti dell'Universo. Consiglio di legare questo articolo con quello apparso da poco sullo scutoide che ne è la giusta e più moderna prosecuzione.

Una domanda senza risposta

Una delle domande fondamentali riguardanti la Natura (e quindi l'Universo) rimarrà forse senza risposta. Sintetizziamola:

la Natura usa il linguaggio della matematica o siamo noi che cerchiamo di descriverla adottando questo linguaggio?

La risposta assume risvolti filosofici e addirittura teologici. Cerchiamo di evidenziare alcuni punti fondamentali.

Se la matematica fosse realmente il linguaggio della Natura, sarebbe universale e come tale tutte le civiltà del Cosmo dovrebbero capirsi una con l'altra. Non confondiamolo, però, con il linguaggio parlato. Gli abitanti di Vega difficilmente capirebbero l'inglese così come noi avremmo grossi problemi con il vegano. Ma, la lingua parlata è ben lontana dal significato profondo di linguaggio. Potremmo sempre venire a un compromesso e utilizzare dei segni e, anche se con grande fatica, alla fine potremmo intenderci. Maggiori difficoltà esisterebbero se fosse proprio diverso il modo di esprimere le proprie sensazioni e riflessioni. Noi utilizziamo le parole, i vegani potrebbero utilizzare i colori e le loro sfumature... o anche solo la musica. E perché non gli odori, come succede per molti animali?

Questa è comunque una scelta che può essere benissimo molto differenziata, ma che poco ha a che fare con il reale significato di un concetto fisico. Per semplificare, potremmo dire che in qualsiasi lingua ci esprimessimo otterremmo un risultato perfetto utilizzando forme geometriche o formule matematiche. A partire dal teorema di Pitagora per finire all'equazione di campo di Einstein. Se così fosse daremmo ragione alla risposta che accetta il linguaggio della matematica come il vero linguaggio utilizzato dall'Universo. Cambierebbe solo il modo "pratico" con cui le varie civiltà lo sanno esprimere.

Matematica concettuale e non matematica espressa con simboli, con parole, con colori o con odori. Forse, se così fosse, una lingua veramente più universale di tutte le altre, potrebbe essere quella basata sui colori, in quanto essi sono legati al mezzo di comunicazione e informazione più usato nell'Universo, la luce. Tuttavia, dobbiamo andare cauti... se qualche specie intelligente non avesse occhi potrebbe, magari, essere sensibile alle più deboli onde gravitazionali e quindi esprimere gli stessi concetti in modo completamente diverso e praticamente incomprensibile. Ma questo è solo un esempio che si rifà a una nostra recente conquista, ossia quella di aver verificato che Einstein aveva ragione.

Chissà quante altre forme di comunicazione ha l'Universo che noi non immaginiamo nemmeno, pur parlando sempre in linguaggio matematico... Forse dovremmo chiedere ai soli abitanti dell'Universo che non cambiano caratteristiche in qualsiasi angolo remoto essi siano. Parlo, ovviamente, delle "particelle" che costituiscono la materia e l'energia: fotoni, elettroni, neutroni, protoni, neutrini sono gli stessi ovunque. Purtroppo il loro linguaggio è ancora in gran parte segreto, a tal punto che riescono facilmente a superare molte leggi fisiche fondamentali della nostra conoscenza terrena, quali la velocità della luce (entanglement), certe barriere energetiche  (effetto tunnel), ma anche a bloccarsi davanti a una misura perfetta, momento decisivo per qualsiasi trattazione matematica (principio di Heisenberg). Per non parlare della doppia (multipla, in verità) essenza degli stessi abitanti,  capaci di agire sia come onde che come oggetti solidi (doppia fenditura, effetto fotolelettrico).

Le cose sono, perciò, ancora più complicate e ben lungi dall'essere risolte con la sola "nostra" matematica. Come vi dicevo si fa presto a cadere nella filosofia o, più facilmente ancora, nella teologia. Consideriamo tutto ciò una premessa e occupiamoci di cose molto più pratiche e alla portata di chiunque. Possiamo ammettere, senza tema di essere smentiti, che la Natura AMI particolarmente certe forme geometriche. Il nostro linguaggio matematico a volte sa spiegare il perché, altre volte tenta solo soluzioni abbastanza traballanti.

Abbiamo visto che l'Universo è entusiasta della forma a spirale. Una forma che è stata studiata fin dall'antichità e che nel medioevo, giudicato così "buio", un certo signor Fibonacci è riuscito a esprimere con un'operazione veramente elementare: scrivere il numero successivo come somma dei due antecedenti. La sezione aurea che tanto aveva ispirato l'arte greca e tutta quella che ne è seguita (fino ai nostri giorni) nasceva quasi automaticamente... e con essa, la spirale.

Più passa il tempo e più la serie di Fibonacci e i suoi numeri sbocciano un po' ovunque, come il tarassaco in un qualsiasi giardino.

Abbiamo capito perché? Non del tutto e le spiegazioni variano a seconda dell'organismo vivente o non vivente che la mostra, dai più piccoli ai più grandi. Per le chiocciole si segue una certa linea di ragionamento fisico (e, quindi, matematico) che è diverso da quello che comanda la forma di molti fiori, per non parlare dei cicloni atmosferici o delle immense galassie. Più che un linguaggio matematico della Natura, sembrerebbe di avere a che fare con un gioco molto divertente. Sempre che tutto non sia regolato da quelle "terribili" particelle dell'infinitamente piccolo, fotoni ed elettroni ci hanno abituato a giochi d'equilibrismo veramente pazzeschi!

Di Fibonacci, della sezione aurea, di spirali abbiamo parlato spesso e ne parleremo di nuovo molto presto.

Occupiamoci adesso di un'altra forma che sembra anch'essa molto amata dalla Natura: l'esagono regolare. Per entrare nel vivo del discorso permettetemi di utilizzare la mia solita "favoletta", in modo che i concetti che andiamo ad esprimere siano facilmente trasferibili anche ai più giovani (malgrado la tristezza dell'inciviltà e dell'ignoranza che ci circonda, resto sempre, in fondo in fondo, ottimista sulle capacità di reazione dell'essere umano... i grandi greci, le antiche civiltà sumerica, egiziana, cinese, maya, ecc. e lo splendore dell'arte medioevale e rinascimentale europea mi lasciano un filo di speranza per un ritorno dell'uomo al pensiero e alla voglia di conoscenza).

Nove punti cercano casa

Immergiamoci, per semplicità di trattazione, in un mondo a due sole dimensioni e che sia anche completamente piano. Ma sì, consideriamo proprio il mondo di Flatlandia...

A nove punti, giunti da molto lontano e molto amici tra loro, viene assegnata una certa area per costruirsi la casa, una per ogni punto.  I nove amici decidono  di utilizzare la stessa forma  e, seguendo le regole della nazione che li ha ospitati, essa deve essere un poligono regolare.  I nove amici, prima di scegliere, vogliono rifletterci bene,  per cercare di limitare sia i costi che  la fatica manuale. Essendo esperti in matematica, si ricordano che a parità di area (quella assegnata che non può essere cambiata), aumentando il numero di lati del poligono, diminuisce il perimetro. Diminuire il perimetro, vuol dire consumare meno mattoni (risparmiare soldi) e faticare meno (risparmiare energia).

Usiamo una matematica ultra semplice per descrivere le conclusioni dei nove amici.

l'area di un poligono regolare è data dal prodotto del perimetro per l'apotema diviso due, ossia:

A = p · a/2

il perimetro risulta quindi:

p = 2A/a

Il che vuol dire che a parità di area si ottiene un perimetro minore al crescere dell'apotema. Ma, essi sanno anche che l'apotema non è altro che il raggio del cerchio iscritto nel poligono. Devono perciò cercare di prendere l'apotema più grande possibile per ottenere il minimo perimetro a parità di area. Non è difficile concludere che l'ideale sarebbe decidere per un numero infinito di lati, ossia far coincidere il poligono con il cerchio stesso di raggio r = a.

L'area a loro disposizione vale πr² e , ponendola uguale a 1, ottengono subito il raggio con cui descrivere il perimetro della loro casa ideale che gli permetta di usare il minor numero di mattoni.

πr² = 1

r = 1/√π

Magnifico!

Iniziano subito a segnare per terra i limiti delle loro case e decidono di metterle una accanto all'altra, come mostra la Fig. 1.

Presentano addirittura due progetti, leggermente diversi, e fanno domanda di edificazione.  L'incaricato, giunto sul posto, però, boccia le loro proposte, dato che all'interno delle loro nove  case vi è terreno pubblico non più utilizzabile. Accidenti! Devono rinunziare  alle loro case circolari. Di conseguenza devono scegliere poligini regolari diversi...

Quali potrebbero andare bene? Cominciano con il triangolo equilatero e questa soluzione li soddisferebbe (Fig. 2a), ma il numero di mattoni da utilizzare sarebbe veramente notevole.

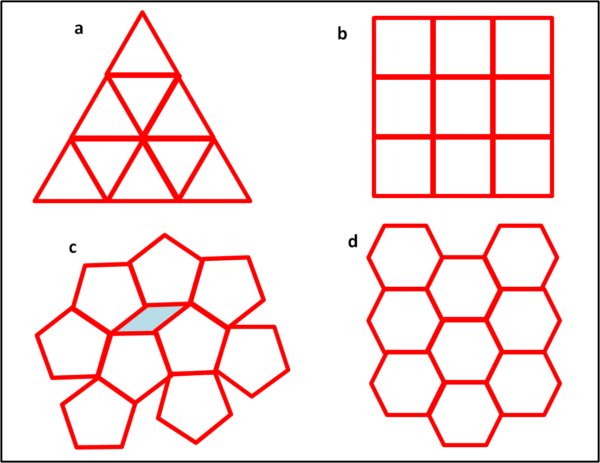
Provano con il quadrato (b), ma anche con questa soluzione il perimetro scende di poco. Magari potrebbero usare il pentagono (c)... No, non va bene, dato che gli resta spazio non utilizzabile. Stanno quasi decidendo per il quadrato, quando uno dei punti si ricorda delle case che fanno alcuni insetti molto laboriosi, che cercano veramente di usare meno materiale (cera) e di risparmiare tempo. Essi vengono chiamati flatapi e riescono a usare l'esagono (d).

Perfetto! Il perimetro è ovviamente sceso e hanno una accostamento senza spazi vuoti. E' inutile proseguire... non esiste altro poligono che permetta di escludere spazi vuoti tra le case e che gli permetta di stare molto uniti tra loro.  I nostri nove punti si ritengono soddisfatti: non potevano fare di meglio con il minimo sforzo e con la minima spesa.

Morale della favola: se si è è da soli, il cerchio è la figura migliore. Se si è in compagnia è necessario venire a un compromesso: diminuire il perimetro (ossia l'energia che si spende), ma non lasciare spazi vuoti. Un discorso perfettamente matematico? Sì, forse... ma analizziamo meglio come si comporta la Natura.

La Natura decide a priori o durante la sua evoluzione?

Traduciamo in termini più fisici la nostra favola. L'ideale per fare ciò è considerare una bolla di sapone. Ricordando i vecchi tempi, prepariamo una giusta mistura di acqua e sapone e poi soffiamo con una cannuccia. Oggi ci sono modi più semplici e più tecnologici per ottenere tante bolle di sapone (cerchietti vari e cose del genere), ma la soddisfazione di riuscire a ottenere la mistura giusta e di veder crescere sempre di più una singola bolla all'estremità libera della cannuccia, mentre i suoi colori cambiano continuamente, si è persa del tutto (provare per credere!).

La forma della bolla è una perfetta sfera (cerchio nel mondo di Flatlandia). Perché? Beh... le molecole di aria che sono contenute all'interno della bolla tendono a distanziarsi e ad occupare la maggiore area possibile, ma per evitare che il tutto scoppi, le molecole della pellicola che si crea attorno alla bolla cerca di contenere l'ingrandimento dell'area e di minimizzare il perimetro attraverso la tensione superficiale che è in pratica il lavoro necessario per aumentare la superficie senza "strappare" il bordo esterno. Lavoro vuole dire energia e quindi le molecole superficiali cercano di minimizzarla e far sì che siano contente sia le molecole interne sia loro stesse, quelle  a contatto con l'ambiente esterno. Un perfetto compromesso che si traduce, ovviamente nella forma sferica. Gonfiamo la nostra bolla in Fig. 3a.

Tutto bene? Sì, ma adesso vogliamo aggiungere una bolla alla prima. Le due bolle sono costrette a scendere a un nuovo compromesso e a dividersi il territorio. Lo fanno secondo un segmento (Fig. 3b). Aggiungiamone una terza. La faccenda si complica, ma il compromesso è ancora trovato e inizia a saltare fuori un angolo molto particolare, quello pari a 120° (Fig. 3c): i tre segmenti che delimitano le tre bolle  lo sottendono tra di loro. Un angolo che fa già pensare alla conclusione... In Fig. 3d è stata aggiunta una quarta bolla. Non può più esserci un punto in comune per le quattro bolle, ma il compromesso si trova aggiungendo un ulteriore segmento, mantenendo immutato l'angolo tra i segmenti. Ormai la nascita dell'esagono risulta quasi ovvia, proprio grazie all'angolo che è stato "scelto". In Fig. 4 abbiamo il risultato ottenuto con 7 bolle, più che esauriente per i nostri scopi: l'esagono si mostra in tutta la sua semplicità e armonia.

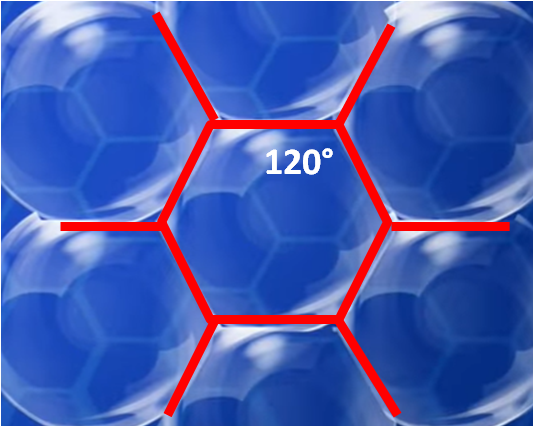
Volendo andare ancora più nel "tecnico" potremmo dire che l'angolo di 120°, quello che comanda la forma finale, è il  più meccanicamente stabile quando su un unico punto agiscono tre forze  che vogliono ottenere l'equilibrio. Ma, è inutile approfondire troppo la questione.

Una configurazione del tutto simile poteva anche essere ottenuta lavorando con la pura matematica, attraverso il diagramma e le "celle" di Voronoi. Abbiamo già detto che le forme poligonali delle celle possono essere ottenute allargando l'area a disposizione di ogni ogni "seme" (andatevi a rileggere questo articolo che merita sicuramente una maggiore attenzione, visti i risvolti a cui si è arrivati in biologia molecolare). Bene... facendo questo, ecco che dalla Fig. 5a, dove vi sono celle che crescono, si ottiene la Fig. 5b, in cui le celle devono fermarsi e venire a un compromesso. Le figure finali sono "quasi" sempre degli esagoni, soprattutto quando la disposizione dei semi (in pratica, i "punti" di Flatlandia) partono da configurazioni molto regolari (le celle di partenza di questi casi le abbiamo segnate in rosso).

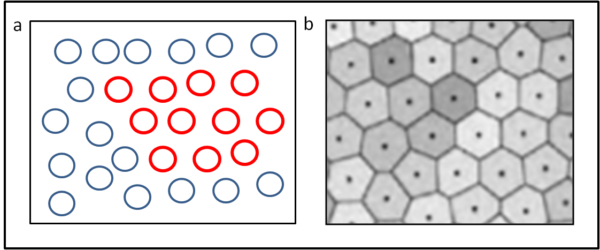
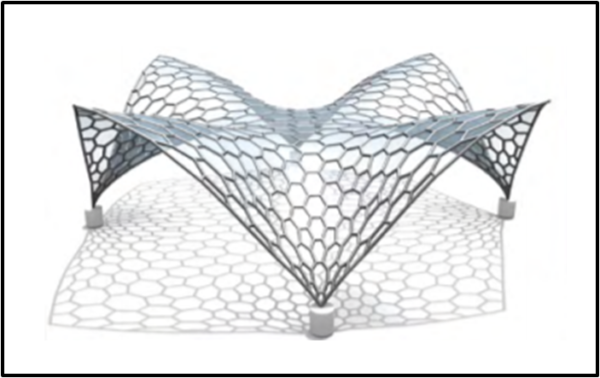
Ogni tanto ci "scappa" qualche pentagono e la forma è irregolare, ma questo diventa importante soprattutto quando i semi non partono da configurazioni regolari o la superficie smette di essere piana. Il discorso ci porta rapidamente agli scutoidi di recentissima scoperta. I prismi esagonali assumono forme più complesse proprio per meglio rispondere alle sollecitazioni esterne e per sistemarsi al meglio sul tessuto epiteliare che, certo, non è piano. Una sezione esagonale "modificata" sapientemente... L'architettura moderna non si è certa fatta scappare certi insegnamenti naturali, come vediamo in Fig. 6

A questo punto potremmo concludere che sembra proprio che la Natura utilizzi forme geometriche, descrivibili perfettamente con il linguaggio matematico. In qualche modo tutto nasce già seguendo queste regole? Regole che condizionano a priori i processi fisici?

La faccenda si complica (o si semplifica) cambiando palcoscenico naturale. Finora abbiamo analizzato forme legate a energia ed equilibrio strutturali, proprio come nelle costruzioni artificiali basate sulla matematica. Tuttavia, l'esagono la fa da padrone anche nelle attività di altri "alieni", ossia delle api. Guardiamo i loro alveari e l'esagono diventa l'essenza stessa. Potremmo dire: "E' ovvio... le api hanno capito le proprietà delle sezioni esagonali!". Non mi dispiacerebbe certo essere d'accordo, dato che questo vorrebbe dire che le api sono in grado di riflettere, pensare, decidere... proprio alieni ricchi di cervelli superiori (sapete come la penso sulle potenzialità animali, mai studiate abbastanza).

Tuttavia, la faccenda potrebbe riportarci allo stesso meccanismo precedente. Le api farebbero delle forme a sezione circolare, ma poi il calore le farebbe allargare, rendendo morbida la cera e permettendo alle "celle" di assumere la forma esagonale. C'è anche chi pensa che sia stato un segno evolutivo e che le api, a furia di provare, abbiano imparato automaticamente a utilizzare la forma di minimo sforzo con il massimo spazio. In altre parole, una "scelta" dovuta all'evoluzione e non a una decisione o a un meccanismo del tutto indipendente che agisca su tutte le forme che non seguono le regole "naturali". Fatto sta che gli alveari sono una meraviglia di regolarità, come mostra la Fig. 7.

Si potrebbe concludere che anche la biologia segue le stesse leggi della materia non vivente. Probabilmente sì, dato che analogo risultato lo possiamo ammirare nella composizione degli occhi degli insetti. Essi non sono semplici, ma composti da un numero enorme di componenti ottiche di forma esagonale, come illustra la Fig. 8

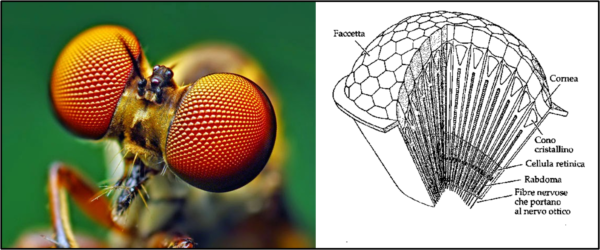
Il discorso si amplia e ci porta rapidamente agli scutoidi di recentissima scoperta. I prismi esagonali assumono forme più complesse proprio per meglio rispondere alle sollecitazioni esterne e per formare al meglio il tessuto epiteliare che, certo, non è piano. In entrambi i casi non può certamente esserci stata una volontà, sempre che non si pensi che anche le singole cellule abbiano la capacità di decidere e scegliere. Sembra più ovvio che sia proprio un risultato dovuto a una scelta evolutiva.

Possiamo ritrovare gli esagoni anche in un processo geologico che ha veramente del prodigioso: le colonne di lava indurita, tipo quelle fantastiche della "strada dei giganti" vicino a Belfast, nell'Irlanda del Nord, ma anche in varie parti del mondo (Fig. 9),

o nella famosa Devils Tower, nel Wyoming, resa celebre dal film di Spielberg "Incontri ravvicinati del terzo tipo" (tra parentesi in quel film gli alieni comunicano con suoni e colori...).

In Fig. 10 la possiamo vedere nella sua maestosità e potremmo anche scegliere un processo fisico molto "diverso" e "leggermente" leggendario, dove la sua formazione si deve a un orso gigantesco che cerca di raggiungere delle innocenti fanciulle, lasciando sulla roccia i segni delle sue unghiate (tra parentesi le fanciulle, volate libere, in cielo sono diventate le Pleiadi).

A parte le splendide leggende, il processo fisico è in qualche modo simile a quello delle bolle di sapone, anche se, in parte, invertito. Immaginiamo una colata lavica che ricopre il terreno. Lentamente si raffredda e la roccia tende ad occupare meno spazio e nasce la solita lotta tra tensione superficiale e materia interna a "celle" di lava indurita. La lava si spacca cercando, ovviamente, di avere le fratture formanti angoli di 120° (equilibrio meccanico), da cui la solita forma esagonale delle colonne, dalle dimensioni simili tra loro (materiale omogeneo e parimenti resistente).

Potremmo chiudere qui il nostro articolo, rimanendo senza una decisiva risposta alla domanda iniziale. Vale, però, la pena di ricordare un altro esagono, di dimensioni decisamente maggiori: il famoso esagono polare di Saturno.

Atmosfera, cicloni, temperatura, ma anche musica e recentemente colori. Come dicevamo negli articoli a lui dedicati è proprio la musica il linguaggio dell'Universo e la matematica la sua migliore traduzione? Come diceva Pitagora (mica l'ultimo arrivato): " La geometria delle forme è musica solidificata".

Restiamo con tanti dubbi, comprendendo, però, sempre più a fondo la gioiosa armonia dell'Universo, sempre che, in tutto ciò, non ci sia lo zampino un po' diabolico e sempre scherzoso delle particelle elementari che vivono nel mondo di Alice. Forse il loro linguaggio non è assolutamente "matematico", ma per farci contenti lo fanno apparire tale nel macrocosmo, quello in cui noi possiamo parlare...