Categorie: Astronomia Elementare Matematica Meccanica Celeste Pianeti Terra
Tags: astronomia geogebra geometria sistema solare Terra Venere
Scritto da: Arturo Lorenzo
Commenti:9
Geometria (N)ello Spazio - Venere e la Terra (*)
Questo articolo è stato inserito nelle sezioni d'archivio "Astronomia classica", "Geometria dello spazio" e "Venere: la dea della bellezza"
E' bello scoprire anche aspetti artistici e geometrici in ciò che avviene nell'Universo. Nei giorni scorsi, desideroso di avere un mio modello geometrico da cui ricavare in qualsiasi momento la distanza tra Venere e la Terra, ho implementato nel solito software Geogebra le orbite dei due pianeti. Entrambe hanno una eccentricità molto bassa (0,0067 per quella di Venere e 0,0167 per quella della Terra). Inoltre la differenza di inclinazione dei rispettivi piani orbitali è piccola. per cui approssimare le due orbite a circonferenze complanari e aventi come comune centro il Sole è , si, una imprecisione, ma in fin dei conti non eccessiva per i miei scopi.
Ho, poi, fatto muovere i due pianeti lungo le rispettive orbite e ciascuno con la propria velocità angolare media (3,2364x10^-7 rad/s per Venere e 1,9924x10^-7 rad/s per la Terra), naturalmente sfasandoli della differenza angolare rilevata al momento della creazione del modello (il 21 dicembre scorso, la distanza angolare tra i due pianeti era di circa 126 °).
Per sapere in qualsiasi momento t la distanza tra i due pianeti, ho considerato il segmento che idealmente li congiunge all'istante t. Tale segmento avrà una lunghezza d(t) variabile nel tempo. Visto che c'ero, ho provato a far partire l'animazione , impostando una sua durata di 8 anni terrestri e un passo di avanzamento di 80 ore. Durante l'animazione ho lasciato visibile il segmento congiungente i due pianeti. Ebbene, godetevi anche voi il risultato finale mentre si forma davanti ai vostri occhi. Il punto giallo centrale è il Sole, il punto celeste è la Terra e quello arancione è Venere.
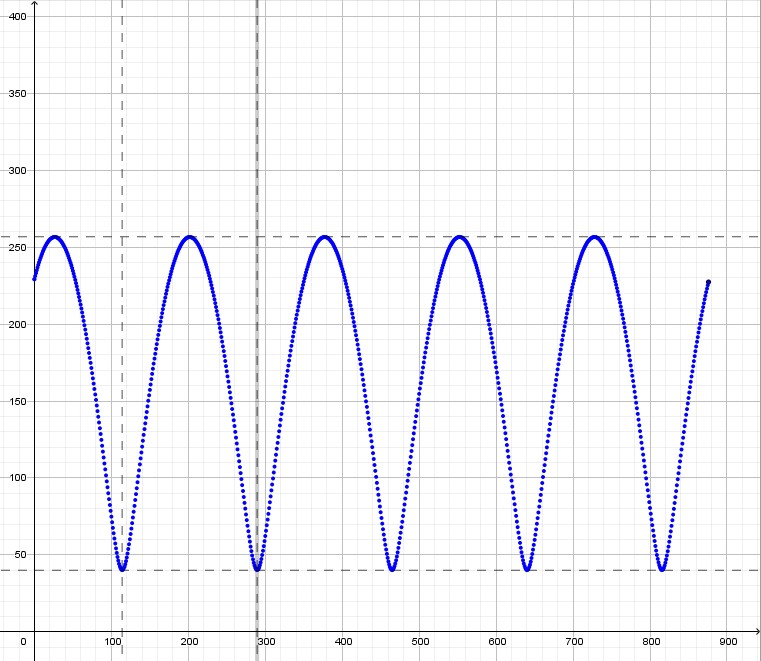
L'obiettivo iniziale del modello geometrico è stato comunque raggiunto. Allego di seguito l'andamento della distanza tra i due pianeti al variare di t.
Nella figura, l'asse delle x è quello dei tempi (una unità corrisponde a 80 ore), mentre su quello delle ordinate è riportata la distanza. Venere e la Terra si danno appuntamento ogni 585 giorni terrestri, circa, quando la loro minima distanza è approssimativamente di 39 milioni di kilometri. Quella massima è, invece, di circa 260 milioni di kilometri.
Qui trovate un articolo di Vincenzo sui due pianeti.
[Appendice]
Procedura seguita per realizzare il modello geometrico con Geogebra
Prima di tutto , ho lavorato nel piano, quindi non con i Grafici 3D. Ho posizionato il Sole nell'origine degli assi x e y. Ho fatto disegnare al software la circonferenza avente centro nell'origine degli assi e raggio pari a quello medio dell'orbita terrestre. Naturalmente, poiché parliamo di milioni di kilometri, ho impostato come unità di misura in geogebra la quantità 10^7 metri (cioè 10 milioni di kilometri) . Essendo il raggio orbitale medio reale della Terra , pari a 148, 350 milioni di km, ho impostato, quindi, il raggio della circonferenza in geogebra pari a 14,835 unità. Stesso discorso per l'orbita di Venere, avente stavolta raggio orbitale medio
in geogebra pari a 10,821 unità.
A questo punto dovevo individuare la posizione dei due pianeti sulle rispettive orbite al generico istante di tempo, tenuto conto delle rispettive velocità angolari medie, che ho indicato con e
. Sapendo che la Terra compie un giro completo attorno al sole in circa 365 giorni, mentre Venere lo fa in circa 225 giorni (intesi sempre come giorni terrestri), ho calcolato le due velocità angolari medie con la formula:
dove T è il periodo , ossia la durata di un giro completo, espresso in secondi. Quindi, nel caso della Terra T= 365*24*3600=31.536.000 s. Nel caso di Venere, invece, T=225*24*3600=19.440.000 s.
Ho così ottenuto i valori delle velocità angolari medie dei due pianeti, che ho richiamato nell'articolo.
Ho poi impostato in geogebra la variabile t, corrispondente all'unità di misura del tempo. Partendo dalla posizione iniziale, il pianeta Terra, muovendosi lungo la sua orbita, all'istante di tempo t spazzerà un angolo pari a . La posizione iniziale della Terra al momento della costruzione del modello (21 dicembre scorso) è stata da me ricavata mediante consultazione di uno dei tanti planetari disponibili online. In particolare, io ho utilizzato solarsystemscope. Ho così constatato che, guardando il sistema solare dal polo nord celeste, e adottando lo stesso sistema di riferimento O,x,y di geogebra, la Terra si trovata quasi esattamente nel punto di coordinate (0, -Rt). Partendo da questa posizione iniziale , man mano che la Terra avanza lungo l'orbita (ruotando attorno al Sole in senso antiorario), le sue coordinate cartesiane nel sistema di riferimento in geogebra, all'istante di tempo t, saranno quindi date da:
Allo stesso modo ho individuato la posizione di Venere che, il 21 dicembre scorso, risultava in avanti rispetto alla Terra di circa 126°, quindi , considerata la posizione iniziale della Terra vista sopra, risultava a 36° (126-90) dall'asse x, nel primo quadrante. Pertanto, le coordinate cartesiane del pianeta Venere nel sistema di riferimento in geogebra , all'istante di tempo t, saranno date da:
A questo punto, per visualizzare i due pianeti ho disegnato due punti Pt (di colore celeste) e Pv (di colore arancione), aventi rispettivamente le coordinate e
.
Ho poi collegato i due punti con un segmento, impostandone visibile la traccia.
Infine, per la variabile temporale t ho impostato uno slider con valore iniziale zero, valore finale 252.288.000 s (pari a 8 anni terrestri) e incremento 288.000 (pari a 80 ore).
A questo punto, si attiva l'animazione sulla variabile t e il risultato è quello proposto nell'articolo.
9 commenti
grazie Artù! un magnifico regalo per tutti!
Bellissimo! mi piacerebbe vedere tutti i passaggi che hai fatto con Geogebra.
Li trovo sul sito di Geogebra o li puoi inserire qui ?
Grazie e BUON NATALE
Giorgio, posso spiegare qui i passaggi seguiti. Intuisco che tu conosca questo software.
Prima di tutto , ho lavorato nel piano, quindi non con i Grafici 3D. Ho posizionato il Sole nell'origine degli assi x e y. Ho fatto disegnare al software la circonferenza avente centro nell'origine degli assi e raggio pari a quello medio dell'orbita terrestre. Naturalmente, poiché parliamo di milioni di kilometri, ho impostato come unità di misura in geogebra la quantità 10^7 metri (cioè 10 milioni di kilometri) . Essendo il raggio orbitale medio reale della Terra ,
pari a 148, 350 milioni di km, ho impostato, quindi, il raggio della circonferenza in geogebra pari a 14,835 unità. Stesso discorso per l'orbita di Venere, avente stavolta raggio orbitale medio 
in geogebra pari a 10,821 unità.
A questo punto dovevo individuare la posizione dei due pianeti sulle rispettive orbite al generico istante di tempo, tenuto conto delle rispettive velocità angolari medie, che ho indicato con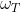
e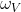 
. Sapendo che la Terra compie un giro completo attorno al sole in circa 365 giorni, mentre Venere lo fa in circa 225 giorni (intesi sempre sempre giorni terrestri), conoscendo i rispettivi raggi orbitali medi, ho calcolato le due velocità angolari medie con la formula:
dove T è il periodo , ossia la durata di un giro completo, espresso in secondi. Quindi, nel caso della Terra T= 365*24*3600=31.536.000 s. Nel caso di Venere, invece, T=225*24*3600=19.440.000 s.
Ho così ottenuto i valori delle velocità angolari medie dei due pianeti, che ho richiamato nell'articolo.
Ho poi impostato in geogebra la variabile t, corrispondente all'unità di misura del tempo. Partendo dalla posizione iniziale, il pianeta Terra, muovendosi lungo la sua orbita, all'istante di tempo t spazzerà un angolo pari a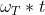
. La posizione iniziale della Terra al momento della costruzione del modello (21 dicembre scorso) è stata da me ricavata mediante consultazione di uno dei tanti planetari disponibili online. In particolare, io ho utilizzato solarsystemscope. Ho così constatato che, guardando il sistema solare dal polo nord celeste, e adottando lo stesso sistema di riferimento O,x,y di geogebra, la Terra si trovata quasi esattamente nel punto di coordinate (0, -Rt). Partendo da questa posizione iniziale , man mano che la Terra avanza lungo l'orbita (ruotando attorno al Sole in senso antiorario), le sue coordinate cartesiane nel sistema di riferimento in geogebra, all'istante di tempo t, saranno quindi date da:
Allo stesso modo ho individuato la posizione di Venere che, il 21 dicembre scorso, risultava in avanti rispetto alla Terra di circa 126°, quindi , considerata la posizione iniziale della Terra vista sopra, risultava a 36° (126-90) dall'asse x, nel primo quadrante. Pertanto, le coordinate cartesiane del pianeta Venere nel sistema di riferimento in geogebra , all'istante di tempo t, saranno date da:
A questo punto, per visualizzare i due pianeti ho disegnato due punti Pt (di colore celeste) e Pv (di colore arancione), aventi rispettivamente le coordinate)
e )
.
Ho poi collegato i due punti con un segmento, impostandone visibile la traccia.
Infine, per la variabile temporale t ho impostato uno slider con valore iniziale zero, valore finale 252.288.000 s (pari a 8 anni terrestri) e incremento 288.000 (pari a 80 ore).
A questo punto, si attiva l'animazione sulla variabile t e il risultato è quello proposto nell'articolo.
La
caro Artù,
se hai voglia potresti anche inserire il tuo commento nell'articolo... ci starebbe bene e verrebbe sicuramente letto di più...
Veramente notevole. Complimenti per il lavoro!
Bellissimo grazie.
Come spesso mi capita vedrò di copiare il lavoro fatto, grazie ancora anche per aver pubblicato il percorso seguito per ottenere il risultato. Bravo!
Lavoro interessante non solo per l'immagine artistica che ne esce.
A prima vista non avrei pensato che la distanza avesse un andamento così regolare.
Un domanda. Come si rapporta il periodo della distanza con quelli dei due pianeti?
Ciascun pianeta ha, ovviamente, il proprio periodo. Per la Terra è 365,25 giorni , per Venere è 224,70 giorni. Data una configurazione iniziale del sistema Terra-Sole-Venere, la stessa configurazione si ripete dopo 8 anni circa, cioè 2920 giorni. Se divido 2920 per il periodo della distanza Terra-Venere (584 giorni), ottengo 5, quanti sono i lobi del disegno che si forma nell'animazione. Sarà un caso ?
Aggiungo che nel frattempo ho provato anche con la coppia Marte - Terra
Come mi aspettavo, stavolta il disegno che viene fuori facendo muovere il segmento congiungente i due pianeti non si chiude perfettamente e facendo proseguire ulteriormente l'animazione, i nuovi lobi interferirebbero con quelli già tracciati. Le due orbite, infatti, non sono almeno approssimativamente concentriche. Anche la distanza minima e quella massima tra i due pianeti è diversa da quella che si ottiene semplicemente sottraendo e sommando i raggi medi delle due orbite. Quello che, invece, mi torna, confrontandolo con altre fonti, è il periodo con cui i due pianeti . Marte e Terra, si danno appuntamento alla minima distanza: circa 780 giorni (26 mesi). Allego l'immagine ottenuta e l'andamento della distanza tra i due pianeti.