La sfera di Hill. 2 ***
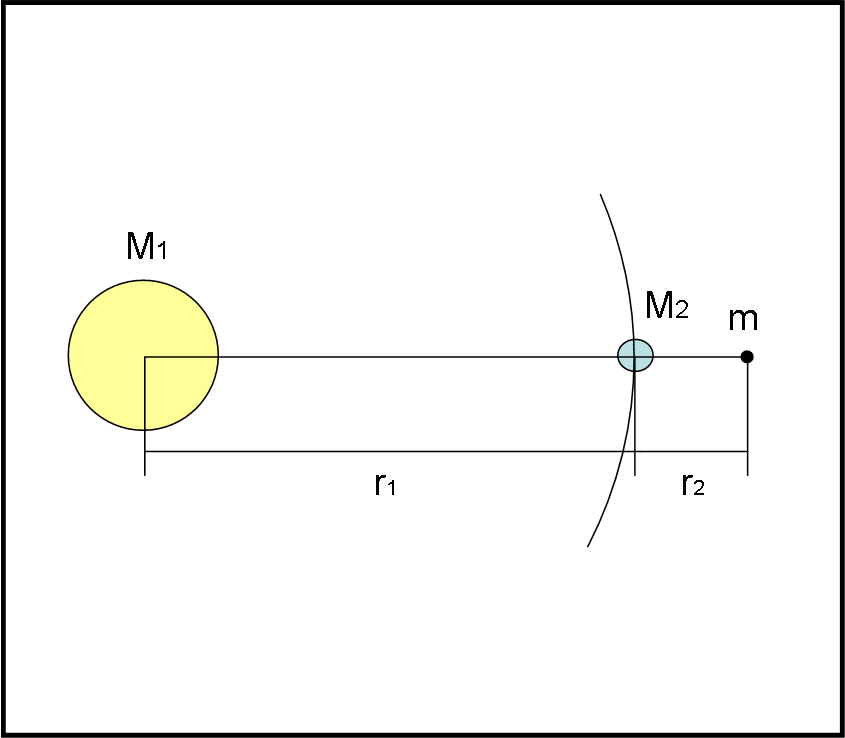
Mettiamoci nelle condizioni in cui il satellite stia dalla parte più lontana della sua orbita rispetto alla stella di massa M1. In altre parole, il satellite sia in fase “piena” permanente (Fig. 1). Assumiamo, cioè, che la velocità angolare del satellite attorno alla massa M1 sia uguale a quella attorno al pianeta di massa M2. Sia r1 la distanza tra M1 e M2, e r2 la distanza tra M2 e il satellite di massa m. Queste condizioni possono essere prese come limite per la sfera di Hill.
Le condizioni di equilibrio per il pianeta (uguaglianza tra forza centrifuga e forza di gravità) si ha quando:
M2ω2r1 = GM2M1/r12
Da cui:
ω2 = GM1/r13 …. (1)
Il satellite deve muoversi con la stessa velocità angolare sotto l’effetto delle due forze di gravità (quella di M1 e quella di M2),
mω2(r1 + r2) = GmM1/(r1 + r2)2 + GmM2/r22
Sostituendo ω, ottenuta dalla (1), abbiamo:
GmM1(r1 + r2)/r13 = GmM1/(r1 + r2)2 + GmM2/r22
M1(r1 + r2)/r13 = M1/(r1 + r 2)2 + M2/r22
Riduciamo tutto allo stesso denominatore (r13(r1 + r 2)2 r22) che non può mai essere zero.
M1(r1 + r2)3r22 = M1r13r22 + M2r13(r1 + r2)2
Eseguiamo il cubo di un binomio
M2r13(r1 + r2)2 = M1 r22(r13+3r12r2+3r1r22+r23) – M1r13r22
M2r13(r1 + r2)2 = M1r23(3r12+3r1r2+r22)
A questo punto si possono eseguire due approssimazione tenendo conto che r2 << r1
(r1 + r2)2 ≈ r12
e
3r12 + 3r1r2 + r22 ≈ 3r12
L’equazione si riduce a:
M2r15 ≈ M1r23(3r12)
Dividendo per r12, si ha:
M2r13 ≈ 3M1r23
Da cui:
r2 ≈ r1 (M2/3M1)1/3
Devo dire, però, che non mi piace molto… preferisco la versione precedente, meno precisa, ma più … elegante.






7 commenti
GRANDISSIMO ENZONE!
VERAMENTE UN GRANDISSIMO ARTICOLO, DEGNO DEL NOBEL!!!
Ho esagerato un tantino?
Che volete ragazzi, me lo devo tenere buono
tenetemi...se no lo sbrano!!!!


Alvy.... mi sa che siamo rimasti soli... abbiamo fatto sparire tutti???!!!
Hai visto che notizia BOMBA?
No Enzo, di che si tratta?
Sto calcolando il raggio di Hill risolvendo l'equazione non approssimata per valutare lo scostamento in tre diversi casi:
Sole-Terra
Terra-Luna
Sole-Saturno.
Lo sai che ho la mente malata no?
Allora Enzo, ho ottenuto i seguenti risultati.
Sistema TERRA-LUNA
- raggio di Hill approssimato: 61.360 km
- raggio di Hill non approssimato: 64.450 km
- scostamento: 4,8%
Sistema SOLE-TERRA
- raggio di Hill approssimato: 1.500.691 km
- raggio di Hill non approssimato: 1.505.000 km
- scostamento: 0,3%
Sistema SOLE-SATURNO
- raggio di Hill approssimato: 65.269.655 km
- raggio di Hill non approssimato: 66.200.000 km
- scostamento: 1,4%
Dai valori degli scostamenti sembra, come era forse da attendersi, che il sistema Sole-Terra sia quello che meglio approssima la condizione di approssimazione (rapporti di distanze e masse) della formula semplificata.
Ora voglio provare a risolvere l'equazione di L2 per fare i relativi confronti con il raggio di Hill.
Situazione finale.
Sistema TERRA-LUNA
- raggio di Hill approssimato: 61.360 km
- raggio di Hill non approssimato: 64.450 km
- scostamento: 4,8%
- distanza L2 non approssimata: 64.300 km
Sistema SOLE-TERRA
- raggio di Hill approssimato: 1.500.691 km
- raggio di Hill non approssimato: 1.505.000 km
- scostamento: 0,3%
- distanza L2 non approssimata: 1.500.000 km
Sistema SOLE-SATURNO
- raggio di Hill approssimato: 65.269.655 km
- raggio di Hill non approssimato: 66.200.000 km
- scostamento: 1,4%
- distanza L2 non approssimata: 66.200.000 km.
non siete soli. questo universo (blog) brulica di vita