Categorie: Matematica Riflessioni
Tags: eliminazione James Bond possibilità quiz sicurezza soluzione
Scritto da: Vincenzo Zappalà
Commenti:2
Soluzione al quiz sulla spia ****
Per risolvere questo quiz, non veramente proibitivo, è necessario farsi uno schema accurato e completo di tutte le configurazioni possibili e, poi, eliminarne un po' alla volta, fino a che garantiscano una risposta esatta. Ovviamente, Fabry e Paolino lo hanno risolto brillantemente.
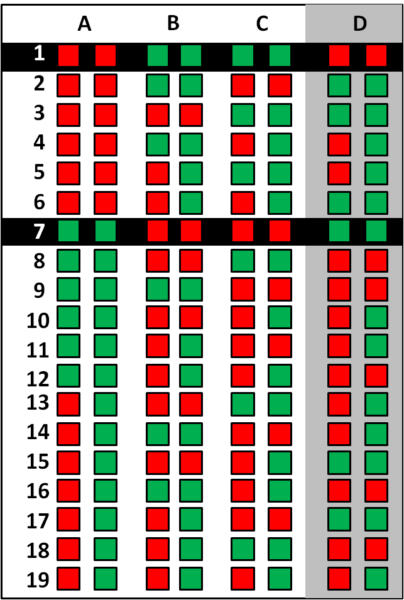
Le combinazioni possibili sono 19 (ovviamente avere un rosso e un verde sulla fronte equivale ad averne un rosso e un verde, ossia non conta l'ordine, ma il numero). E' fondamentale tenere anche in conto le possibili disposizioni dei francobolli che il direttore D tiene nascosti. Riportiamo di seguito lo schema generale:
Il primo a parlare è A. La sua risposta è PASSO, il che vuol dire sicuramente che lui non vede sulla fronte di B e C due coppie di francobolli dello stesso colore. Se, ad esempio ne vedesse due rossi sulla fronte di B e due rossi sulla fronte di C sarebbe sicuro di averne due verdi! Analoga situazione se invece di quattro rossi ne vedesse quattro verdi. Possiamo perciò escludere le situazione 1 e 7.
Il secondo a parlare è B. Anche questa volta la sua risposta è PASSO. In realtà, la risposta precedente cambia ben poco le possibilità di B. Anche lui, non vedendo 4 francobolli rossi o verdi sulle fronti di A e C, deve dire PASSO e permettere di escludere le configurazioni 2 e 8.
Il terzo a parlare è C. Anche lui dice PASSO, il che vuol dire eliminare (come prima) le configurazioni 3 e 9. Tuttavia, il suo PASSO regala un'informazione in più...
Se C fosse nelle condizioni 4 o 10, potrebbe essere sicuro di non avere due francobolli verdi o due francobolli rossi , dato che se li avesse, una delle spie precedenti avrebbe indovinato. Il suo PASSO, quindi, elimina anche queste due possibilità.
Ricomincia a parlare A. Se lui si trovasse nelle condizioni 13 o 14 sarebbe nelle stesse condizioni della spia precedente (C). Dato che risponde PASSO elimina anche queste due possibilità.
Non è ancora finita, però… se A fosse nelle condizioni 15 o 16 potrebbe pensare di avere due francobolli verdi o due rossi. Ma questo è impossibile, perché se così fosse C avrebbe già indovinato. Avrebbe perciò la sicurezza di avere un francobollo rosso e uno verde. Però, continua a dire PASSO e quindi anche la 15 e la 16 possono essere eliminate.
Tocca ora, nuovamente, a B. Ma B, avendo davanti agli occhi la situazione delle possibilità ELIMINATE, non ha molto da pensare! Infatti, tutte le configurazioni rimaste portano allo stesso risultato: lui può avere soltanto un francobollo rosso e uno verde sulla propria fronte. Per cui B dice, senza un alcun dubbio, LO SO.
Il nostro James si salva, come previsto, ma siamo costretti a dire che oltre che bravo è stato anche fortunato ad avere quella posizione!
Il quiz lo trovate qui







2 commenti
Ho provato ad illustrare la soluzione mettendo su un grafico a tre dimensioni le possibili affrancature. Su ciascuno degli assi ci sono le combinazioni relative a ciascun prigioniero. A è l'asse blu, B il giallo e C il magenta. Il ragionamento è lo stesso, ma mi sembra che in questo modo si evidenzi meglio.
Nella figura sotto ci sono le possibili combinazioni iniziali.
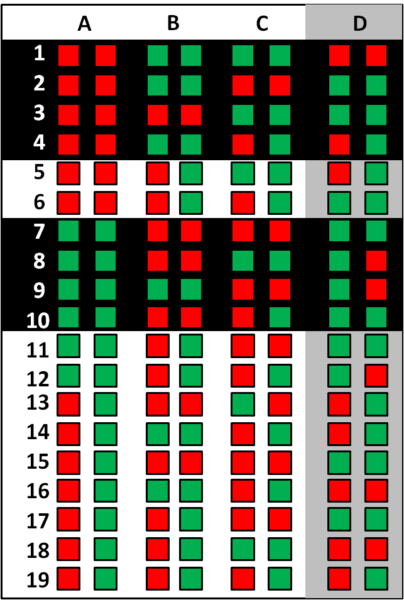
Nelle tre combinazioni di ciascun segmento blu varia solo l'affrancatura di A, mentre non variano quelle di B e C. Se su uno di questi segmenti c'è solo una combinazione valida (intermittenti) allora se A vedesse quella combinazione di BC sarebbe certo anche della sua. Poiché A passa, queste combinazioni sono da scartare.
Nella figura sotto il cubo è ruotato in modo da avere l'asse di B (giallo) che va in profondità. Su ciscuno dei segmenti gialli varia l'affrancatura di B, mentre non variano quelle di A e C. A seguito del 'passo' di B possiamo scartare le combinazioni intermittenti con un ragionamento analogo a quello fatto per A.
Le due figure sotto evidenziano i casi da scartare dopo il 'passo' di C ed il secondo 'passo' di A.
La situazione che si presenta a B è quindi quella in figura sotto. Tutte le combinazioni rimaste permettono di identificare l'affrancatura di B. Inoltre, qualsiasi sia la combinazione di A e C, B ha sempre l'affrancatura rosso-verde.
caro Fabry,
probabilmente hai anche ragione... ma sono preso da Maxwell e da impegni "extra-blog". Lascio a te la prosecuzione delle analisi. Mi sembri proprio una... spia!