Categorie: Relatività
Tags: Minkowski quiz relatività ristretta simultaneità
Scritto da: Vincenzo Zappalà
Commenti:45
QUIZ “antipasto” per lo spaziotempo di Minkowski ***/****
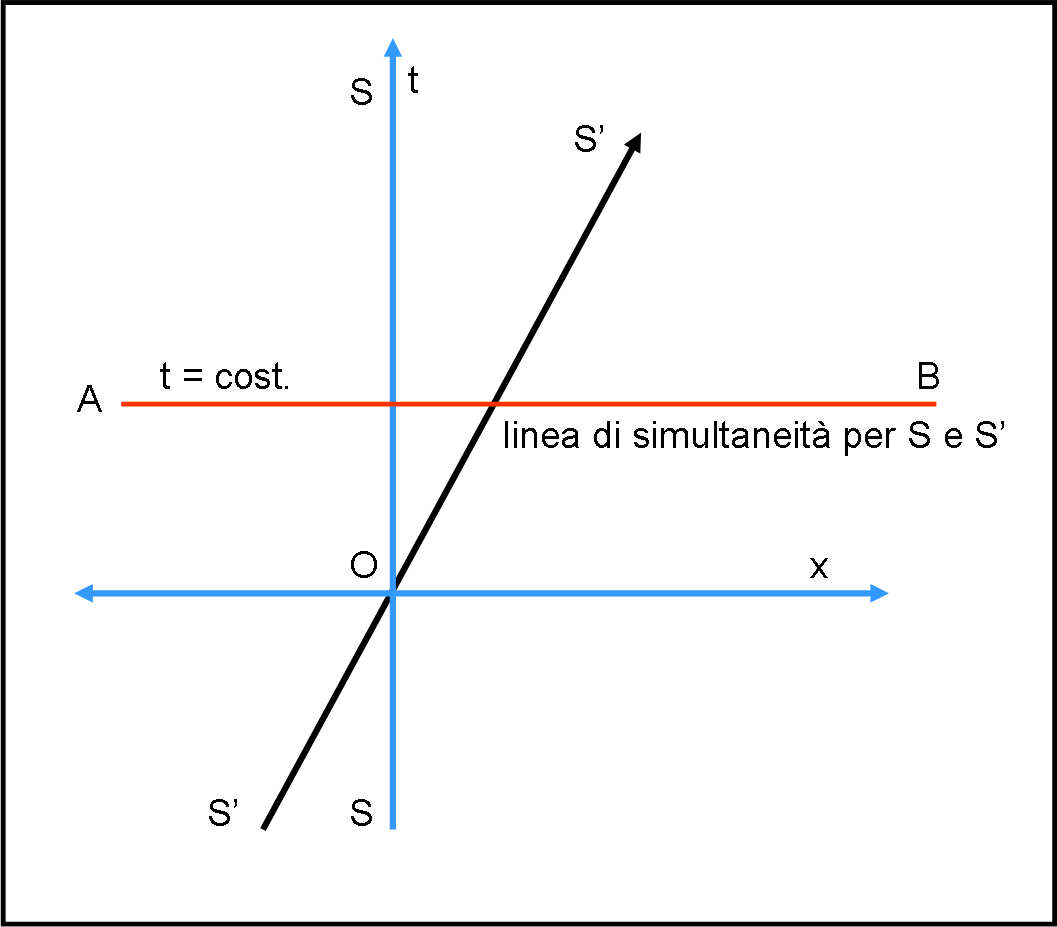
Costruiamo uno spaziotempo a due dimensioni (t,x), apparentemente del tutto uguale a quello che è stato usato per spiegare la relatività galileiana. L’asse verticale è il tempo t e l’asse orizzontale lo spazio x. Il sistema di riferimento S considerato fermo è quello di color blu.
Un punto O che sta su di esso (in realtà dovremmo parlare di evento) si muove SOLO lungo l’asse del tempo t. Non ha velocità e quindi lo spazio x percorso deve essere sempre zero. S’ è invece un sistema di riferimento che si muove con una certa velocità v rispetto a S. La sua traiettoria nello spaziotempo (t,x), che possiamo chiamare linea di Universo, è una retta inclinata di un certo angolo rispetto a quella verticale e questo angolo dipende direttamente dalla velocità di S’ rispetto a S.
Se fossimo nello spaziotempo di Newton e Galileo, il tempo si misurerebbe sempre lungo t per qualsiasi sistema inerziale. In altre parole, il tempo di chi viaggia lungo S’ rimarrebbe sempre t. Ciò vuol dire che il tempo sarebbe assoluto. Stesso tempo vuole anche dire che in qualsiasi sistema inerziale la simultaneità dei fenomeni si determinerebbe attraverso una retta parallela all’asse x (la retta per la quale il tempo è costante).
La Fig. 1 illustra questa situazione galileiana che avevamo già affrontato in dettaglio. La retta AB determina la simultaneità sia per il sistema S che per il sistema S’ in movimento rispetto a lui.
Purtroppo la relatività di Einstein ci ha dimostrato, utilizzando la trasformazione di Lorentz, che le cose non vanno affatto così, soprattutto se le velocità relative sono paragonabili alla velocità della luce. In particolare, abbiamo imparato che ogni sistema di riferimento S’ in movimento ha un suo tempo proprio che appare dilatarsi se visto dal sistema S. Nel nuovo spaziotempo di Minkowski bisogna che questa caratteristica venga rappresentata correttamente. Per rendere tutto più semplice, l’unità di misura dello spazio e del tempo è stata scelta in modo che la retta a 45° descriva un sistema che si muove alla velocità dalle luce. In altre parole inseriamo il ben noto cono di luce, o –ancor meglio- la sua intersezione con il piano (t,x).
A causa della relatività del tempo, segue che l’asse del tempo del sistema S’ non può essere più l’asse t. Il nuovo tempo t’ di S’ deve essere misurato da un orologio che viaggia insieme a S’ e, quindi, l’asse del tempo t’, relativo a S’, è proprio la traiettoria descritta da S’. Questo orologio appare rallentare se visto nel sistema di riferimento S, ma su questo ci torneremo molto presto. A noi, adesso, interessa ricavare il nuovo asse x’ relativo all’asse t’.
Questo nuovo asse è quello che deve rappresentare la simultaneità nel sistema S’. Infatti, l’asse x è quello che indica fenomeni simultanei nel sistema (t,x), dato che gli eventi con t costante sono quelli che si ottengono lungo una retta parallela a x. La stessa cosa non può certo capitare per il sistema S’. Il suo tempo scorre lungo S’ e non coincide più con t: ogni sistema ha il suo tempo, dato che il tempo non è più assoluto. Inoltre sappiamo già bene, che anche la simultaneità è relativa ed è ora di mettere in pratica questo concetto.
La domanda che vi faccio è quindi molto semplice concettualmente: “Come può fare S’ a disegnare nel sistema di riferimento S della Fig. 1 la sua linea di simultaneità x’?”. Potrei anche fermarmi qui e non darvi nessun aiuto ulteriore (chi vuole può provare… per lui valgono i quattro asterischi).
Per gli altri aggiungo qualche nota “pratica”, illustrata in Fig. 2.
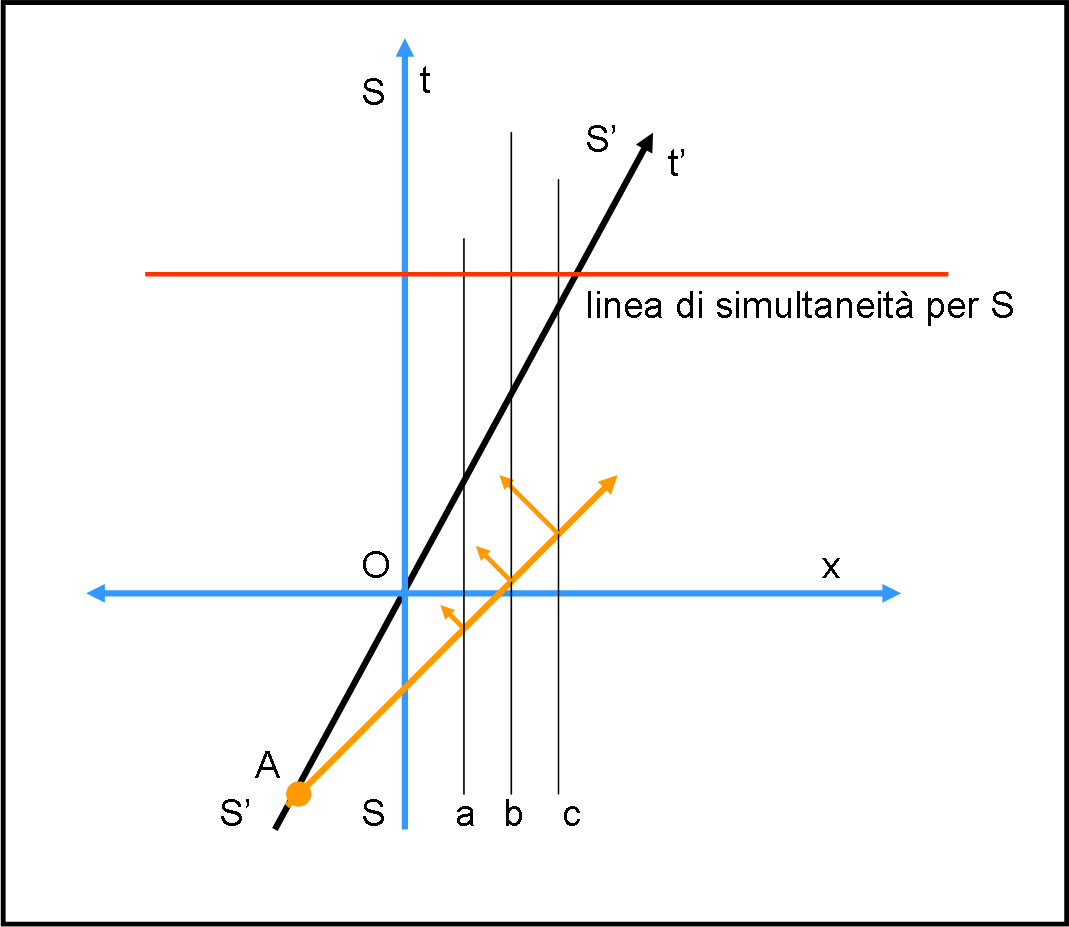
Il nostro sistema S’ ha molti amici (a,b,c) nel Cosmo, anzi nello spaziotempo, e sono tutti disponibili ad aiutarlo. Essi sono fermi rispetto a S e quindi descrivono anch’essi linee di Universo verticali. S’ porta con se una lampadina molto potente che accende quando si trova in A (A è un evento in quanto è descritto da uno spazio e da un tempo). La luce viaggia alla sua velocità costante ed è facilmente descrivibile nel piano (t,x).
Non appena i vari e infiniti amici a,b,c,… ricevono il segnale di luce inviata da S’ quando era in A inviano immediatamente un segnale luminoso con la loro personale lampadina, altrettanto potente. L’operazione di tutti questi amici è del tutto inutile per S’, tranne quella di un solo amico. Il suo segnale, ricevuto da S’, gli permette di tracciare la sua retta di simultaneità. La domanda è: “Quale dei suoi amici cosmici è l’unico utile allo scopo e quale ragionamento logico deve fare S’ per tracciare la sua linea di simultaneità?”.
Una volta tracciata, il nostro sistema S’ capisce perfettamente come costruire questa retta, senza aver più bisogno dei suoi amici spaziali. Gli basta conoscere l’inclinazione del suo asse del tempo t’ rispetto a t. La successiva domanda è quindi: “Che caratteristica geometrica deve avere la linea di simultaneità rispetto a t'?” Ovviamente, desidero anche che dimostriate geometricamente questa conclusione.
Vi pregherei di rispondere esaurientemente a tutte le domande e non solo in modo parziale e vago. Capire la logica del discorso vuole già dire aver fatto un passo decisivo per orientarsi nello spaziotempo di Minkowski, l’unico capace di descrivere graficamente la relatività ristretta e le sue conseguenze.
Forza, coraggio e nessuna paura di sbagliare! Anche se alla fine apparirà come l’uovo di Colombo, il diagramma di Minkowski rimane un vero colpo di genio. Riuscire a capire la sua logica è un’impresa non certo immediata e banale. Comunque, invito tutti a provare. Chi ha voglia di pensare può già rendersi conto che superare questo piccolo quiz vuole anche dire aprire una finestra enorme per la comprensione del celeberrimo paradosso dei gemelli!
Buon lavoro!






45 commenti
Caro Enzo, mi sono fermato alla prima domanda (le altre le leggo dopo) perché volevo buttare giù così di botto come ho pensato di affrontare con un approccio grafico il problema.
come ho pensato di affrontare con un approccio grafico il problema.
Vorrei provare ad andare per ragionamenti progressivi.
Il primo problema che volevo evidenziare è lo scarto temporale necessario affinché l'informazione di un evento raggiunga un “osservatore”, ossia percorra la distanza che separa S da S' alla velocità della luce C.
Le due figure mostrano due eventi, uno accade in S' e viene visto da S e l'altro accade in S e viene visto da S'.
http://www.astrobin.com/full/34214/B/
http://www.astrobin.com/full/34214/C/
La velocità della luce costituisce un limite invalicabile, per cui ogni punto nello spazio tempo può essere raggiunto dall'informazione solo entro i limiti (cono di luce passato) fissati dalla velocità della luce (retta a 45°) e l'informazione che parte da quel punto spazio temporale può raggiungere solo “osservatori” posti entro i limiti dettati sempre dalla velocità della luce (cono di luce futuro).
Le due rette inclinate a 45° (m=1, ossia in 1 anno viene percorso 1 anno luce), limitano (nel passato e nel futuro) e contengono l'informazione di un certo evento.
http://www.astrobin.com/full/34214/D/
Tornando ai due sistemi S ed S', il grafico precedente in realtà non è sufficiente per descrivere fino in fondo la situazione.
La luce viaggia sempre alla medesima velocità, indipendentemente dal sistema di riferimento.
Ora nei disegni precedenti la luce è stata rappresentata con rette inclinate di 45° rispetto all'asse X, ossia al sistema di riferimento di S, ma S' si muove con una certa velocità rispetto ad S ed il suo percorso spaziotemporale non è certo rappresentato da una retta parallela all'asse x.
Se traccio una retta inclinata di 45° rispetto alla retta che rappresenta S', la rappresentazione della velocità della luce vista da S' è diversa rispetto a quella vista da S.
http://www.astrobin.com/full/34214/E/
Ora, ammettiamo che S decida di porre una serie di orologi sincronizzati fra loro sul percorso (asse x) e che quindi la nuova misurazione del tempo secondo il sistema S tenga conto dello scarto temporale dovuto al tempo che la luce impiega per percorrere lo spazio che li separa, comunque i due sistemi non possono misurare il tempo nello stesso modo, poiché la velocità della luce deve essere uguale per entrambi.
L'ultima figura mostra proprio questa situazione
http://www.astrobin.com/full/34214/F/
Nel grafico ho semplicemente ruotato i due segmenti, rosso e blu, che rappresentavano i due diversi modi di vedere C, ho però anche riportato la formula che lega i due diversi modi di misurare il tempo in funzione della velocità di allontanamento di un sistema dall'altro.
Comunque anche solo graficamente appare evidente che se si considera S fermo, secondo il suo sistema di misura del tempo, S' non può che misurare il tempo come se questo scorresse più lentamente rispetto agli orologi sincronizzati di S.
Ora mi leggo le altre domande, sperando di non aver detto qualche sciocchezza.
Paolo
Gulp di nuovo troppe figure... per cui il messaggio si blocca.
Paolo
caro Paolo,
devo leggerlo con calma perché non capisco bene come vuoi arrivare alla risposta della prima domanda... Inoltre vedo nell'ultima figura un tempo t' segnato su una linea verticale... Così a occhio ti direi subito che non va bene, dato che t' si misura lungo la retta nera, anzi la retta nera è proprio l'asse del tempo t', così come per chi non si muove l'asse del tempo è proprio la linea verticale lungo cui si muove...
Comunque, è facile che non abbia capito bene cosa vuoi dire...domani mattina mi metto d'impegno...
Occhio Paolo... la velocità della luce è sempre la stessa in ogni sistema di riferimento (secondo postulato) e non cambia la sua direzione. Il diagramma si riferisce a un solo sistema di riferimento e gli altri sono relativi a lui... A noi interessa sapere come si vede in questo sistema di riferimento la linea di simultaneità di quello in moto...
Ok, spero di aver capito quale grafico realizzare.
Due brevi ragionamenti.
Per il sistema S la linea di simultaneità è parallela all'asse x e ciò vale anche per gli infiniti amici a, b, c, ecc.
Perciò, ho chiesto aiuto ad altri due sistemi che si muovono con la medesima velocità di S', che ho chiamato S'' e S'''.
Dato che si muovono alla stessa velocità, il loro asse del tempo è lo stesso, per cui anche il loro asse x' deve essere uguale per tutti e perpendicolare all'asse t' (angolo di 90°).
Anche in questo caso l'asse x' dovrebbe rappresentare proprio la simultaneità tra i tre diversi sistemi S'; S'' ed S'''.
http://www.astrobin.com/full/34214/G/
D'altronde per considerare S' fermo (cambiando sistema di riferimento), basterebbe ruotare il sistema di coordinate t'x' fino a far coincidere l'asse t' con t e di conseguenza l'asse x' coinciderà con x, per cui il nuovo sistema di coordinate non può che avere le stesse caratteristiche del vecchio (compresa la linea di simultaneità)
http://www.astrobin.com/full/34214/H/
Tornando alla figura iniziale, l'amico posto in a, si trova esattamente nella posizione spaziotemporale intersecata dalla retta che rappresenta la simultaneità del sistema S' quando questo passa per il punto O.
http://www.astrobin.com/full/34214/I/
Quindi quando S' passa per l'origine degli assi del sistema S, l'amico a si trova esattamente sulla stessa linea di simultaneità, per cui la luce parte da a nello stesso tempo misurato dal sistema S' quando attraversa O.
La luce impiega un certo intervallo di tempo Δt' per percorrere lo spazio Δx' e raggiungere il sistema S', ma questa sia per S' sia per S, viaggia sempre alla medesima velocità C (forse prima sono stato frainteso con la figura E volevo mostrare cosa non funzionava, ossia che C deve essere uguale per qualunque sistema di riferimento e quindi non può essere diversa, semmai sono le misure di tempo e spazio che si “adattano” per garantire tale costante).
Dato che l'amico a si trovava sulla stessa linea di simultaneità quando S' ha attraversato O, conoscendo il valore di Δt' è possibile risalire al punto da cui è partita la luce dall'amico a (basta tracciare la retta a 45° che rappresenta la luce e vedere dove interseca la linea di simultaneità del sistema S'), che ovviamente si trova esattamente sulla retta che rappresenta la luce partita dall'evento A (lampadina accesa all'inizio da S').
Per disegnare tale situazione, prima traccio la retta che rappresenta t' (per il sistema S' in movimento a velocità V) e che parte dal punto A, attraversa l'origine degli assi O del sistema S e prosegue.
Poi traccio la retta a 45° che passa per il punto A e rappresenta la luce partita dall'evento A.
Dopodichè traccio la perpendicolare a t', per costruire l'asse x' del sistema S' e lo faccio coincidere il punto O.
Infine traccio la retta a 45° che rappresenta la luce partita dall'amico a.
http://www.astrobin.com/full/34214/J/
Come si vede il segmento della retta che rappresenta la velocità della luce C, è la medesima ipotenusa per due triangoli, uno ha per cateti Δt' e Δx' e l'altro Δt e Δx.
Mi fermo qui
Paolo
caro Paolo,
non poso spiegare a fondo il perché (per non aiutare gli altri), ma le cose non funzionano così... Innanzitutto, tu avresti solo ruotato un sistema, ma la relatività non ruota, bensì dilata e contrae. Posso solo dirti di non importi la perpendicolarità degli assi e pensare bene a cosa vuol dire simultaneità degli eventi per un orologio che viaggia su t'.
Sì, forse, hai ragione... era meglio prima impostare il nuovo diagramma e poi fare quiz... ma secondo me si può fare... bisogna applicare qualcosa che è molto simile alla sincronizzazione degli orologi e sfruttare adeguatamente il fatto che la luce rimane costante e che se anche il tempo è costante vuol dire che lo spazio dà luogo alla linea di simultaneità.
Ti assicuro che è come l'uovo di Colombo, basta una linea o poco più e un piccolo ragionamento logico che deve fare chi viaggia su t'....
Se riusciamo in questo esercizio, potremmo analizzare il paradosso dei gemelli già prima di tutto il resto...
caro Paolo,
forse ho capito il tipo di "errore" che stai facendo... tu vuoi disegnare sul grafico un nuovo sistema di riferimento che non sia legato a S. E' come se su uno steso diagramma tu volesi disegnare due digrammi e non uno solo. Per far ciò non fai che ruotare l'asse del tempo e ti trasporti dietro quello delle ascisse. Il diagramma, invece, vuole rappresentare tutti i sistemi di riferimento che si muovono rispetto a S, visti nel sistema di S, con le loro dilatazioni e contrazioni che seguono la relatività. Se tu volessi cambiare sistema di riferimento "privilegiato" (chiamiamolo così, ma non è esatto), le stesse cose che capitano a S' capiterebbero a S. Ricordati che la simultaneità vista da due sistemi in moto deve essere diversa e che questa diversità non è certo solo dovuta a una rotazione pura e semplice...
Basta, non voglio confonderti le idee...
forza ragazzi!!!
solo Paolo ha coraggio? Vi giuro che non è difficile... basta rileggersi la parte sulla simultaneità...
Stavolta mi chiamo fuori Enzone, per .... manifesta incapacità!
Il fatto è che sono concentrato sulle SNIa e la RR sto ancora leggendola, per cui non voglio scrivere inesattezze, altrimenti sai che randellate....
Ti informo che proprio ieri ho acquistato un simpatico libro di H. Poincarè. "Geometria e caso. Scritti di matematica e fisica" - Bollati Boringhieri 2013.
Confesso che mi ha molto attratto la presenza del problema dei tre corpi ed una trattazione delle equazioni differenziali.
VIVA LE SUPERNOVAE (mi raccomando il dittongo finale, che in realtà è uno iato) ad alto RED-SHIFT
Buuuuh, che figuraccia!!!!!
 e io che speravo in una tua "relativamente" alta velocità di risposta.
e io che speravo in una tua "relativamente" alta velocità di risposta.
Dai Paolo... sei tutti noi!
Caro Enzo, prendo spunto dal tuo suggerimento e dal caloroso sollecito, però non assicuro di non collezionare qualche altra brutta figura..
Tra l'altro, possibile che sono l'unico disposto a collezionare brutte figure?
Diceva Cimabue: “ma che cagnara sbagliando s'impara”.
Comunque, riprovo con un altro approccio.
Mostro subito la figura che ho realizzato e provando a spiegare come l'ho ottenuta.
http://www.astrobin.com/full/34214/K/
Per il sistema fisso S l'evento A dista dal punto O una certa distanza, misurabile sull'asse x, che ho definito Δx A-O.
Anche l'amico b è egualmente distante dal punto O (Δx O-b = Δx A-O).
L'amico b è fermo come O nello spazio e si muove all'unisono nel tempo (dato che entrambi sono fermi).
La luce viaggia sempre alla stessa velocità C, per cui necessariamente impiega lo stesso tempo per percorrere la distanza A-O, la distanza O-b e di nuovo la distanza b-O (dovuta a b che accende la sua lampada appena arriva la luce dell'evento A).
Ossia:
t2-t1 = t3-t2 = t5 – t3
Quando il sistema S' raggiunge O, questo corrisponde ad O', dato che sia S che S' in quell'istante si trovano entrambi nello stesso punto dello spazio e del tempo.
Mentre la luce parte da b, O' si muove rispetto ad O, in direzione di b.
O', però, viene raggiunto prima dalla luce rispetto ad O.
Dal punto di vista di S (o meglio del suo sistema di coordinate) la luce raggiunge O' al tempo t4, invece che t5, questo intervallo di tempo (t5-t4) l'ho definito Δt.
Eppure O' per un istante era proprio lì con O.....
Il sistema S, con il suo sistema di misura del tempo potrebbe ritenere che b abbia acceso la lampada troppo presto, dato che la luce ha raggiunto O' prima del previsto.
Graficamente basta trasportare il segmento che rappresenta la luce nel percorso b-O, nell'istante t4 (ovviamente la lunghezza di tale segmento, b1-O, che rappresenta la luce proveniente da b è identica a quella che congiunge b2 ad O nell'istante t5).
b1 non è altro che b nello stesso punto dello spazio, misurato sull'asse x, ma in un tempo antecedente, ovviamente il tempo a cui mi riferisco è quello del sistema fermo S.
Unendo O' (posizione di S' al tempo t4) al punto apparente b1 (posizione “presunta” secondo S della sorgente luminosa, ossia dell'amico b), è possibile tracciare la linea di simultaneità per S' rappresentata nel sistema di coordinate di S.
Aggiungo solo una figura che confronta due diverse velocità per mostrare le relative linee di simultaneità e come queste dipendono dall'inclinazione di t' rispetto a t (ossia dalla velocità di allontanamento di S' da S).
http://www.astrobin.com/full/34214/L/
Tra i due sistemi in movimento (S' e S''), aumentando la velocità aumenta l'inclinazione del loro asse del tempo, per cui di conseguenza aumenta Δx.
La luce viene rappresentata come una retta a 45°, per cui a Δx corrisponde un uguale Δt, con conseguente maggior spostamento b1 rispetto ad a1.
Più la velocità si avvicina a quella della luce, più la linea di simultaneità tende a diventare parallela all'asse del tempo del sistema S.
Mi fermo qui, sperando stavolta di averci azzeccato.
Paolo
caro Paolo,
complimenti per la tua perseveranza che ti fa onore, ma... la soluzione è molto più semplice di quella da te proposta. In qualche modo, c'è un minimo di verità, ma il risultato non va ancora bene.
Posso consigliarti di dedicarti di più al tempo t': è, in fondo, lui che decide la simultaneità nel suo sistema... anche se visto da S.
La soluzione è decisamente più facile e immediata. Pensa bene a chi si muove lungo t' con il suo orologio e vuole sapere il luogo di punti che sono simultanei con il suo orologio. Come si fa per sapere se un evento è simultaneo rispetto a S'? Basta una sola linea tracciata bene e poi dire che per due punti passa un sola retta... Lo so, lo so, ti sto confondendo, ma vedrai che sto dicendo cose semplicissime.
Quando c'arriverai ti batterai sulla fronte!!!! e penserai a quella vecchia formuletta che diceva come la relazione tra tempo e spazio è praticamente identica a quella tra spazio e tempo, cambiando x' in t' e viceversa... Ma, mi raccomando, non usare formule per arrivarci. prima lo risolvi graficamente e dopo vedrai che molte cose vanno al loro posto...
Comunque... bravo Paolo. Tu, almeno, ci stai provando e provando molte cose prendono maggiore chiarezza, anche sbagliando...
ATTENZIONE! Non vorrei che qualcuno avesse interpretato male. Quando dico amici come a,b e c, intendo infiniti possibili amici e non solo quei tre disegnati (ho, infatti messo i puntini dopo c). Anzi, nessuno di quei tre va bene per lo scopo!!!!
Grazie Enzo per la precisazione, poiché faccio parte di coloro che hanno mal interpretato (cercavo la soluzione tra uno dei tre punti a, b, c segnati)...
Come vedi non desisto.
Questa è la soluzione che più mi convince, poi magari non è quella giusta.....
Mi limito per ora (poi se sono sulla strada giusta si può sempre aggiungere qualcosa…) a mostrare la figura che ho realizzato.
http://www.astrobin.com/full/34214/M/
Dato che il punto O è il punto in comune tra i due sistemi e che la velocità della luce è uguale per entrambi, la luce per andare da A ad O passando per l'amico b (che potrei anche sostituire con un potente specchio), compie un certo tragitto.
Per il sistema S il tempo impiegato dall'evento A per raggiungere O è pari a to-tA, ossia Δt.
Per il sistema S' il tempo impiegato dall'evento A per raggiungere O è pari a t'o -t'A.
Ovviamente i due tempi sono diversi, dato che t' è l'ipotenusa di un triangolo rettangolo di cui un cateto è rappresentato da t (l'altro cateto è Δx A-O).
Trasportando il tempo t' (segmento A-O) sull'asse t, si ottiene un intervallo di tempo in più, rispetto al tempo t intercorso tra l'evento A e il suo arrivo in O secondo S.
Ora se per S la linea di simultaneità era orizzontale, per S' questa non può che tener conto di questo differente sistema di misura del tempo, per cui se per S la retta di simultaneità congiunge O a b all'istante to, per S' tale retta non può che congiungere O al tempo t'o trasposto sull'asse t e b al tempo to.
Mi fermo qui, in attesa di capire se sono sulla strada giusta.
Paolo
Aggiungo solo una figura che confronta diverse velocità
http://www.astrobin.com/full/34214/N/
Paolo
scusa Paolo,
ma mi viene quasi da ridere... Stai facendo girare un po' ovunque quest povera retta :). Per dirti che non va ancora bene, potrei solo dirti che con la tua retta vi è simultaneità con eventi del passato e questo è impossibile.... Comunque si deformi il sistema bisogna stare nel futuro.
Un ulteriore aiuto... (te lo meriti per l'impegno): A manda il suo segnale... perché? perché vuole ricevere una risposta a un tempo che può paragonare col tempo che scorre sulla sua linea t'. Ad esempio... perché non fare passare un tempo uguale ad AO? Se gli arriva un segnale in quel momento vuol dire che il tempo impiegato all'andata e al ritorno deve essere.... ????? Ricordiamoci che dt'c deve rimanere sempre uguale se dt' è lo stesso... ossia il segnale tanto ha impiegato a ricevere e tanto ha impiegato a inviare... Guarda meglio una delle figure della simultaneità, quella con la linea tratteggiata...
Comunque meriti un premio e sono convinto che risolto questo problemino più semplice di quanto pensi diventerai un mago anche dalla relatività ristretta e del diagramma di Minkowski... Sono pronto a scommetterci!!!!
aggiungo... cosa succederebbe se S' viaggiasse alla velocità della luce? la sua linea di simultaneità dovrebbe diventare qualcosa di banalissimo.... rispetto a t'....
Vabbè ho capito, ora ci provo anch’io così accompagno Paolo nella collezione di figuracce.
Vediamo.
Mi prendo un qualsiasi punto sulla semiretta S’, che rappresenta un istante t’ qualsiasi del sistema S’.
Devo fare in modo che due (per cominciare) lampadine siano viste accendersi contemporaneamente dall’omino in t’. L’omino non si muove nel sistema S’, per lui scorre solo il tempo.
Devo allora disegnare due rette inclinate a 45° rispetto all’orizzontale (l’angolo compreso tra di esse sarà 90°); si tratta delle due linee di universo delle due luci emesse dalle due lampadine. Queste due rette si devono incontrare in t’.
Le due lampadine devono trovarsi su queste due rette, una delle quali si sviluppa a sinistra e l’altra a destra di S’. In quali punti devono però essere poste?
Beh, se le due lampadine vengono accese simultaneamente in S’ (tutti gli osservatori in S’ hanno gli orologi sincronizzati) le due lampadine dovranno essere equidistanti da t’.
Se impongo l’uguaglianza dei due segmenti lungo le due diagonali a 45° ottengo che le due lampadine si trovano in due punti posti sulla stessa retta orizzontale.
E poi non dire che mi manca il coraggio di espormi ....
No, ho scritto una boiata. Quale che sia l’inclinazione di S’ (ovvero la sua velocità rispetto ad S) otterrei sempre una retta orizzontale. NO!
Mettiamola così:
Mantengo il ragionamento fatto sopra ma modifico la condizione finale.
A dover essere uguale è la distanza tra le due lampadine nel sistema S'. Devo quindi trovare una retta la cui inclinazione consenta l'imposizione della condizione di equidistanza tra le due lampade. In questo modo i due segnali luminosi giungerebbero contemporaneamente in t' se attivati contemporaneamente; quest'ultima operazione è consentita dal sincronismo di tutti gli orologi di S'.
A ben vedere l'unica retta che consente ciò è quella che, passando per l'origine, presenta lo stesso angolo d'inclinazione (rispetto all'orizzontale) di t' (rispetto alla verticale).
Maggiore è la velocità di S' e più si "chiude" il "cono". Quando S' viaggia alla velocità della luce il "cono" si riduce alla bisettrice del primo quadrante cartesiano.
Per onestà devo ammettere che, nel mentre che ragionavo sul quiz, mi è tornata alla mente una figura che devo aver visto parecchio tempo fa su uno dei miei libri: le maglie del reticolo relativistico non sono più quadrate ma romboidali, con l'angolo esposto verso l'origine dgli assi sempre più stretto man mano che aumenta la velocità.
Beh, così mi soddisfa maggiormente.
Va bene, mi ci butto anche io, mal che vada vincerò il premio di consolazione per averci provato (sperando che ci sia).
Secondo me dobbiamo far sì che venga rispettato in ogni caso il postulato della costanza di velocità della luce.
Quindi dobbiamo disegnare gli assi t(x) e t’(x’) in modo tale che la luce vada sempre a velocità c.
Allora per S se poniamo che un centimetro di righello dell’asse x sia 300000 Km e un centimetro sull’asse t sia 1s, la luce (o meglio un sistema che viaggia alla velocità della luce rispetto a S) sarebbe descritto da una retta a 45°.
Adesso poniamo che un sistema S’ abbia una linea di universo a 80° rispetto a x (l’angolo dipende dalla velocità di S’ rispetto a S, basta semplicemente fare due calcoli in base alle scale impostate).
Si nota che se l’angolo è a 45° vorrebbe dire che va alla velocità della luce, e se inferiore va oltre alla velocità della luce, ovviamente impossibile.
L’asse t’ (rispetto a S) è evidente che corrisponde alla traiettoria di S’, quindi è a 80° rispetto a x.
Infatti se un evento O’ è fermo rispetto a S’, per S si muove in x e t e coincide con la linea di universo di S’, ma per quest’ultimo è fermo e quindi coincide con il suo asse dei tempi t’ (nessun spostamento in x’).
Adesso dobbiamo trovare x’.
Dato che la luce è a 45° ovvero è la bisettrice tra t e x, lo deve essere anche di t’ e x’ (la velocità deve essere sempre costante).
Quindi l’asse x’ è a 10° rispetto a x, ovvero t’ e x’ non sono a 90° ma a70°.
La linea di simultaneità di S è parallela all’asse x, mentre quello di S’ è parallela a x’, ovvero a 10° rispetto a x.
Io penso (ma non ne sono del tutto sicuro) che gli assi t’ e x’ siano misurati sempre allo stesso modo di quelli di S, ovvero 1 cm (lo stesso cm dato che non può cambiare) equivale a 1s anche per t’ e 300000km per x’.
Adesso però la misura è in diagonale, quindi occorre fare le proiezioni sugli assi t e x e quindi lo stesso cm non è equivalente per i due sistemi, ovvero viene visto in modo deformato da S (ma per S’ resta tale e quale).
Nel sistema S’ gli eventi posizionati in vari x’ (fermi rispetto a S’) si muovono tracciando rette parallele a t’ e la simultaneità a un certo t’ la si trova tracciando la parallela a x’ e trovando le intersezioni.
Per S’ sono tutti punti che hanno la stessa t’, ma proiettati su t con una retta parallela a x, diventano tempi diversi: ciò che per S’ è simultaneo non lo è per S.
Ad esempio supponiamo di avere il punto x’a e x’b fermi rispetto a S’.
Se a t’=0 tutti e due accendono una lampadina, ovvero i due eventi sono simultanei, un ipotetico x’c che si trova a metà (sull’asse x’) tra loro due, dopo un certo t’z viene raggiunto dai due fasci di luce, che si incontrano in un punto z di coordinate x’c e t’z di S’ (che vanno disegnati facendo delle parallele agli assi t’ e x’).
Per S invece il punto z, che esiste ed è lo stesso dell’altro sistema, avrà delle coordinate date dalle proiezioni di z sugli assi t e x con parallele a t e x (anche se non sono sicurissimo che sia così semplice).
Quello che si può notare è che mentre per S’ la luce è partita simultaneamente a t’=0 dai punti x’a e x’b, per S non solo si trattano di due punti che hanno x diverse, ma anche t diversi (basta fare le proiezioni sugli assi t e x).
Per S la luce che parte da x’b avviene dopo la partenza della luce da x’a.
Spero di aver inquadrato il problema anche solo marginalmente.
Ciao.
Tento la fortuna anch'io
"A" manda il suo segnale, che lungo una retta inclinata di 45° colpisce un ipotetico amico "z", il quale appena vede il segnale fa partire il suo che colpisce S't' in "O".
Il tempo trascorso in S't' è uguale ad AO.
Questo vuol dire che quando S't' si trova a metà strada tra A ed O, z accende la sua lampadina, che viene vista da S't' quando si trova in O.
La linea di simultaneità x' quindi passa per z e per il punto medio di AO.
Oh... finalmente qualcosa si muove oltre al solito "eroe" Paolo! Aspetto ancora un giorno (o anche due) e poi scrivo una risposta che sia oltremodo semplice e immediata per tutti... Dobbiamo riuscire a essere sempre SIMULTANEI!!!!!!
Paolo è un vero grande eroe. Si immola solitario per la scienza. La sua perseveranza e lo sprezzo del pericolo costringono gli altri (me compreso) a non rimanere insensibili e ad esporsi anche quando avrebbero altro da fare (vedi SNIa ).
).
Grande Paolo, sei un pò la locomotiva del nostro circolo.
Ennesimo tentativo ed ennesima figura (spero non di ) ..... hai ragione Enzo sta retta l'ho fatta girare in ogni modo
) ..... hai ragione Enzo sta retta l'ho fatta girare in ogni modo 
La figura mostra l'ennesimo tentativo di posizionare la retta di simultaneità per S'.
http://www.astrobin.com/full/34214/P/
Dunque, S' accende la sua lampada, quando arriva in O, misura con il suo orologio quanto tempo Δt' è trascorso.
Ora se S' fosse fermo si aspetterebbe che se uno dei suoi amici (un ipotetico a) nello stesso istante in cui lui passa per O, accende la sua lampada la luce dovrebbe impiegare il medesimo tempo per raggiungerlo, ossia tanto tempo impiega la luce per andare da A verso il nostro amico, tanto impiega per tornare ad S'.
Tale situazione è quella illustrata con la dicitura “ C percorso con S' fermo”, dove il percorso della luce A-O è identico a quello O-c.
L'ipotetico S' fermo non è altro che S, o meglio un ipotetico amico solidale con S, corrispondente all'evento A, che non si muove nello spazio, ma solo nel tempo.
Dato che S' si muove, tale aspettativa non può che essere delusa, infatti quando S' chiede all'amico b dove si trova e che tempo misura, questo si trova in una posizione spazio temporale ben diversa da quella supposta (a), stando fermi.
Ricapitolando:
S' si aspetta che quando arriva in O, la luce torni versi di lui (grazie alla lampada dell'ipotetico amico a) impiegando lo stesso tempo Δt';
S' si muove, per cui nell'istante in cui raggiunge O, se il suo ipotetico amico a (quello con S' fermo) accendesse la lampada la luce raggiungerebbe S' molto prima rispetto a ciò che accade.
Ora confrontando queste due visioni del tempo e dello spazio, che in comune devono avere la medesima velocità della luce C (ossia le rette che la rappresentano sono sempre di 45°), quando S' raggiunge O l'amico si trova in b e non in a come lui si aspetta.
Nel grafico quando S' fermo è in O (dato che è fermo il suo tempo coincide con t del sistema S), la sua linea di simultaneità (quella del sistema S), pone l'amico che riflette la luce nella posizione a, mentre per S' in movimento l'amico che riflette la luce si trova nella posizione b.
Quindi quando S' in movimento si trova in O, la posizione dell'amico che riflette la luce non è in a, ma in b, per cui la simultaneità per S' si ottiene tracciando una retta che congiunge O a b.
In questo modo è possibile mantenere costante la velocità della luce (che è indipendente da quella del sistema di riferimento, ossia deve essere uguale per S' fermo e per S' in movimento), ma necessariamente deve cambiare la misura del tempo (t' diverso da t) e dello spazio (x' diverso da x).
Avrei altre considerazioni da fare (più aumenta la velocità, più la retta di simultaneità tende a chiudersi verso l'asse t', fino a coincidervi quando V= C) , ma preferisco per ora fermarmi qui in attesa di conferme o smentite sul ragionamento fatto.
Paolo
PS: Se qualcuno decidesse di guardare le figure dell'articolo su relatività e simultaneità http://www.infinitoteatrodelcosmo.it/2015/01/04/la-relativita-speciale-disegnata-da-minkowski-6-sincronizzazione-e-simultaneita/ , non fate come me di dargli solo un occhiata, fate attenzione che il tempo nella figura scorre verso il basso, equivoco che mi ha fatto cercare rette nella direzione sbagliata (sottosopra)
Ciao Paolo.
La figura non mi dispiace (giudizio puramente personale).
Perchè non provi a disegnare il reticolo "cartesiano" s'-t'? Guarda un pò cosa si ottiene?
Poi prova a misurare la distanza (pardon, separazione) tra due eventi posti ai vertici opposti di una cella del reticolo, magari applicando il teorema di Pitagora ....
... ssshhh non dirlo ad Enzo altrimenti si arrabbia. Sai, questa è una mia fissazione .....
Caro Paolino!
il fatto di avere la t invertita è una di quelle situazioni che bisogna sempre tener presente quando si lavora con la RR. Mai fissarsi su una certa visione, ma essere preparati a modificarla e badare ai concetti. La mia non è cattiveria, ma solo volontà di eliminare apparenze che possano influenzare il ragionamento... mi spiace, però, di aver creato un po' di confusione...
Veniamo a noi...
Hai condito il racconto con una parte di speranze disattese che, in fondo, non erano necessarie. S' sa benissimo di muoversi lungo il suo tempo (non può fermarsi rispetto a lui). S' deve solo pensare a guardare il suo orologio nel tragitto AO e misurarlo accuratamente. Non gli interessa niente della luce che gli sta arrivando dai suoi amici "esterni". Solo quando avrà percorso un altro tragitto temporale OB uguale ad AO deve controllare di chi è la luce che gli sta arrivando! Solo quell'amico è quello che gli interessa, dato che tra il ricevere e il rinviare la luce ha impiegato lo stesso tempo di S'. Insomma, b è nel punto di mezzo del percorso della luce che ha è partita da A ed è arrivata in B e quindi la sua "riflessione" deve essere stata simultanea con il passaggio di S' da O.
Hai fatto 30 (come anche altri...) e puoi fare facilmente 31: qual'è la caratteristica che lega la retta t' e la x'? In pratica l'hai detto, ma sarebbe bello che lo dimostrassi geometricamente... (tu che sai fare e inserire le figure ).
).
Bene, molto bene... sapevo di potermi fidare di te! Bravi anche gli altri, ovviamente...
Adesso, scriverò un articoletto di spiegazione per tutti e poi vorrei mettervi alla prova più difficile con il paradosso dei gemelli e la sua apparente mancanza di simmetria. E, invece, la simmetria c'è! Come ci si aspetterebbe nella RR . Sia chi viaggia che chi sta fermo possono dire e rendersi conto che solo chi viaggia invecchia di meno. Lo faremo insieme, solo con la RR, e sarà un esercizio interessantissimo oltre che poco conosciuto!!!
Bravi tutti coloro che hanno risposto e i tanti che hanno letto il QUIZ

Alvy, a dir il vero ho già fatto due altre figure.
La prima confronta velocità diverse e relative (presunte, da parte mia) linee di simultaneità
http://www.astrobin.com/full/34214/Q/
La seconda affronta proprio la questione dal punto di vista geometrico (stesso tempo di percorrenza luce, spesso spazio percorso), analizzando due (più uno) triangoli isosceli.
Che tra l'altro chiarisce un possibile equivoco nel mio precedente post quando parlo di perocorso A-O della luce, in realtà intendo il segmento A-a (ossia al tempo in cui S' raggiunge O), ecc.
http://www.astrobin.com/full/34214/R/
Le figure partono però dal presupposto che il ragionamento fatto sia corretto... se non solita figuraccia.
Paolo
Beh, caro Paolo, sembra che Enzo sia soddisfatto.
Quello che intendo dire è questo: immagina un foglio di carta millimetrata che faccia da sfondo ad un sistema di assi cartesiani (e quindi tra loro ORTOGONALI). Ogni cella del reticolo cartesiano è un quadrato.
Nel nostro caso però i due assi NON sono ortogonali. Cosa si ottiene? Prova a disegnarlo.
Aspetta Alvy, vorrei prima provare a rispondere alla questione che pone Enzo.
Sto facendo una figura, comunque a me sembra che l'asse x' (retta simultaneità di S) abbia lo stesso angolo di inclinazione rispetto all'asse x, e di quello dell'asse t' rispetto a t.
Poi posto la figura.
Paolo
Fai pure quello che stai facendo Paolo e scusa anzi la mia (inopportuna) intromissione.
Volevo aggiungere (e poi mi taccio!) che il problema è appunto quello!
Cioè a dire il fatto che l’asse x’ (retta simultaneità di S) abbia lo stesso angolo di inclinazione rispetto all’asse x, di quello dell’asse t’ rispetto a t.
Ciao e buona domenica
Alvy, non c'è nessuna intromissione, anzi i tuoi interventi offrono sempre un sacco di spunti, per cui non provare a tacere....
Comunque ecco la figura a cui stavo lavorando:
http://www.astrobin.com/full/34214/S/
Paolo
mamma mia... siete scatenati!
Paolo... perché la distanza bb1 deve essere uguale a Oc'??? Da cosa lo deduci?
Non mi piace tanto che si usino linee relative a S con linee relative a S'... Può, prima o poi, creare confusione. Meglio considerare similitudini di triangoli nello stesso sistema...ed è anche più immediato il risultato...
Alvy... cosa intendi con unire gli estremi del parallelogramma? sii esplicito! Ormai siamo alla frutta del quiz...
Tu dici: "Poi prova a misurare la distanza (pardon, separazione) tra due eventi posti ai vertici opposti di una cella del reticolo, magari applicando il teorema di Pitagora "....
SPIEGATI MEGLIO, please...
Volevo aggiungere un appunto riguardo al paradosso dei gemelli.
Mi è venuto un piccolissimo dubbio sulla suddetta questione.
Ovvero il problema è che un osservatore terrestre vede l’astronauta andare al rallentatore, mentre per l’astronauta è il terrestre che va più lentamente.
Ad esempio se per l’astronauta passa un tempo proprio (misurato con un solo orologio solidale con se stesso) di 10 anni per arrivare al pianeta x, per il terrestre l’orologio posto in prossimità del pianeta (sincronizzato perfettamente con quello sulla terra) segna ad esempio 100 anni.
Per l’astronauta invece è il tempo terrestre che dovrebbe scorrere solo di 1 anno: praticamente c’è un conflitto di tempi, ovvero manca la simmetria.
Però l’astronauta misura correttamente il proprio tempo con un solo orologio, e guarda i due orologi solidali al sistema terrestre uno posto sulla terra e uno sul pianeta x.
Questi due orologi, che sono sincronizzati tra loro per il terrestre e che segnano 100 anni, sono in movimento rispetto l’astronauta e quindi sono assolutamente fuori sincronismo (per lui).
Probabilmente per l’astronauta quando arriva al pianeta x, l’orologio del sistema terrestre posto sul pianeta x avanza di un anno, ma è avanti di 99 e quindi segna 100.
In poche parole lui è veramente più giovane, e in più viene mantenuta la simmetria dello scorrere dei tempi.
Se fosse così, ma non mi azzardo a scommetterci, il paradosso si scioglierebbe come neve al sole.
Se è corretto, probabilmente con il diagramma spazio tempo si verificherebbe graficamente quanto detto in modo molto semplice.
Resto in attesa della tua soluzione.
Ciao
Mah, caro Enzo, penso di non dire cose astruse.
Se ho un sistema cartesiano (assi ortogonali s-t) posso tracciare:
- una qualsiasi retta ORIZZONTALE. Tutti i punti (eventi) che giacciono su tale retta sono contemporanei. Di tali rette posso tracciarne quante ne voglio, ciascuna corrispondente ad un diverso valore di t.
- una qualsiasi retta VERTICALE. Tutti i punti (eventi) che giacciono su tale retta occupano la stessa posizione spaziale, sia pure in istanti diversi. Di tali rette posso tracciarne quante ne voglio, ciascuna corrispondente ad un diverso valore di s.
Se traccio infinite (facciamo ... alcune) rette orizzontali e verticali costruirò una rete o maglia che rappresenta punti-eventi di quel sistema.
Ho solo chiesto di fare altrettanto per il sistema "distorto". Non vedo nulla di strano.
Ovviamente Enzone, a conclusione di tutta questa bailamme di idee, grafici, ecc. attendo la tua impeccabile spiegazione di tutto quanto si è discusso.
Sai, devo inserirla nella trattazione della RR che raccoglie tutti gli articoli.
Dunque, per affermare che b-b1 deve essere uguale a O-c’, ho usato il fatto che luce viene rappresentata da una retta inclinata di 45°.
Partendo da tale rappresentazione, ho cercato di dimostrare l'esistenza di un quadrato e di un triangolo isoscele che consentono di dimostrare che b-b1 = O-c’.
La figura mostra il risultato
http://www.astrobin.com/full/34211/B/
Caro Alvy, dopo la tua ultima precisazione penso di aver capito cosa intendi , per cui ho realizzato questa figura (dimmi tu se è quello che chiedevi di descrivere graficamente... scusami ma per provare a realizzare una figura devo prima immaginarmi esattamente cosa rappresentare)
, per cui ho realizzato questa figura (dimmi tu se è quello che chiedevi di descrivere graficamente... scusami ma per provare a realizzare una figura devo prima immaginarmi esattamente cosa rappresentare)
http://www.astrobin.com/full/34211/C/
Paolo
Perfetto Paolo.
Ora, se fossimo in un classico sistema cartesiano (assi ortogonali) le maglie della rete sarebbero rappresentate da QUADRATI.
Per determinare la distanza tra due punti, ai vertici di una maglia quadrata (diciamo, due punti posti su due vertici uniti dalla diagonale della maglia), si applica il teorema di Pitagora.
Nel nostro caso le maglie sono però dei ROMBI. Per trovare la distanza di due analoghi punti (che in questo caso sono eventi, data la presenza del tempo in uno dei due assi) che faccio? Applico il terorema di Pitagora? Direi di no.
Siccome la formula della separazione della RR è molto somigliante al teorema di Pitagora, ad eccezione dell'inversione di un segno, a me sembra che proprio questo fatto divida la geometria euclidea da quella della RR. Ma, d'altra parte, lo S-T di Minkowski è piatto, come la geometria euclidea.
La faccenda si risolverebbe considerando come quarta coordinata (oltre alle tre spaziali) il tempo immaginario anzichè quello reale. Qui mi fermo per non creare confusione, anche perchè credo che Enzo soffra di una grave forma di allergia nei confronti del tempo immaginario.
Volevo solo far notare questa stranezza che Enzone non mancherà di spiegarci e chiarirci (COME PROMESSO! ).
).
Guarda cosa succede al tuo reticolo ed ai ruoi rombi, se S' si allontana da S a V= 0,9 C
http://www.astrobin.com/full/34211/D/
Paolo
Molto bene, molto bene...
non inserisco niente riguardo al paradosso dei gemelli perché lo toccheremo a tempo debito...
Ad Alvy posso solo dire che non intendo inserire "i". ti posso assicurare che se ne può fare a meno. Nessuno pretende, infatti, che si debba scrivere il teorema di Pitagora tale e quale al nostro in uno spaziotempo non euclideo. Proprio perché non è euclideo non vale il teorema di Pitagora, ma esiste comunque un invariate. Preferisco di gran lunga parlare di invariante relativistico che non introdurre il concetto di numero immaginario che comporta una serie enorme di dubbi e incomprensioni. Non è ancora il momento, dai! Oltretutto l'invariante è pur sempre un tempo proprio e quindi facilmente comprensibile. Non mettiamo il carro davanti ai buoi... e avanti con molta calma!
Mi sembra che Paolo sia ormai bello "caldo" per entrare nella RR come nella MQ. Ha scaldato i motori!!!!
Insomma, abbiamo visto come opera la trasformazione sulla forma del campo da gioco. Adesso dobbiamo vedere con che unità di misura si misurano gli eventi... In fondo la RR è tutta qui. Ma prima fatemi riscrivere ordinatamente il concetto di simultaneità e la derivazione degli assi in movimento.
Per l'unità di misura cercherò di seguire l'approccio che ha usato proprio Minkowski con la sua figura originaria... il bello deve ancora venire...
OK Enzone.
Si Paolo, ottimo esercizio.
Non vorrei che a QUALCUNO venisse in mente il ROM(P)BO è la figura che più mi si addice!
Adesso me ne torno alle supernovae.
Informo che negli ultimi due giorni, in cui abbiamo giocato con la RR, l'Universo quasi-statico (al netto cioè di eventuali accelerazioni anomale) ha visto espandere l'orizzonte visibile di 48 ore-luce, ovvero di circa 5*10^10 km.
Se vi sembra poco, si tratta di una lunghezza pari a circa 5 volte il diametro del sistema solare (almeno fino a Plutone).
Buongiorno.
Provo..... Non è l'amico che giace dove passa spazio-likely S? Cioè dove i due orologi si possano sincronizzare nel senso che sarebbero accesi contemporaneamente? Incrocio le dita...
beh... è ovvio che sia così, dato che devono segnare lo stesso tempo. il problema è come disegnare questa linea... Però, può darsi che non abbia capito cosa intendi dire... sei un po' ermetico, spiegati meglio...
Caro Professore
In effetti non so più nemmeno io cosa intendessi.... Cercavo un modo alternativo, con parole mie... Già sapevo che il raggio di luce deve bisecare esattamente gli assi di ambedue i sistemi di riferimento dato che c è la stessa.... Questo mi conferma che non mastico bene l'argomento... E comunque ero come al solito indietro temporalmente (nostro tempo proprio) : ho visto che ha attaccato la costruzione del diagramma nel frattempo..... Adesso mi studierò gli ultimi post. Ancora complimenti.