Categorie: Riflessioni
Tags: fortuna golf logica palline da golf quiz scacchi soluzione
Scritto da: Vincenzo Zappalà
Commenti:0
Soluzione della pallina da golf "anomala" ****
PROLOGO
La discussione basata sull'ironia e sulla presa in giro tra Frank e me non ha voluto creare confusione. In realtà ha voluto solo dimostrare la differenza sostanziale che esiste tra diversi tipi di competizione. Prendiamo proprio il golf (ma andrebbe bene anche il calcio) e gli scacchi. Per abile che sia un golfista e/o un calciatore, anche se cerca di tenere conto di tutti gli accorgimenti tecnici, deve -più o meno- basarsi sulla fortuna, dato che non potrà effettuare un certo tiro (mentalmente perfetto) se le condizioni al contorno non sono quelle ideali. La magica rovesciata di Pelè non riesce tutte le volte, anche se Pelè ha reso minime le possibilità di errore. C'è la piccola spinta di un avversario che non poteva essere prevista, la schiena di qualcuno che devia leggermente il tiro, una folata di vento, una scarpetta un po' più sporca e mille altri eventi non prevedibili. Negli scacchi, invece, tutto è prevedibile e se l'abilità cresce tutto si svolge come preventivato. Detto in parole molto povere: nel primo caso la fortuna ha un ruolo importante e diventa parte stessa del gioco. Nel secondo caso la fortuna sparisce del tutto, dato che ogni mossa può ripetersi con esatta precisione e l'unico ostacolo è l'abilità dell'avversario.
E' ovvio, quindi, che a Frank sembri normale affidarsi a un briciolo di fortuna, mentre invece il quiz deve affidarsi solo sulle reali possibilità in cui il caso non possa assolutamente influenzare le scelte obbligatorie.
Luigis, invece, ha lavorato da scacchista ed è riuscito nel proprio intento.
Come vi dicevo, vi sono metodi leggermente diversi per arrivare alla stessa soluzione. Io ne descrivo uno simile a quello di Luigis, facendomi aiutare da qualche figura e seguendo una identificazione delle palline leggermente diversa.
Chi vuole ancora provare non vada avanti!
Pausa...pausa...pausa
Per potere analizzare la faccenda con metodo rigoroso ordineremo le palline in QUATTRO categorie:
Normali N bianche
Sospette S nere
Sospette Pesanti P rosse
Sospette Leggere B blu
La PRIMA PESATA si effettua mettendo QUATTRO palline su un piatto e QUATTRO sull'altro. Vi sono due possibilità:
(1) La bilancia resta in equilibrio
(2) La bilancia pende da un lato
CASO (1)
Nel caso (1) siamo sicuri che le OTTO palline messe sulla bilancia rientrano nella categoria N, ossia tra loro non vi può essere quella anomala. Tutte e otto diventano BIANCHE.
In questo caso restano QUATTRO palline nere, che sono ovviamente diventate sospette, ossia S. Tra di loro infatti deve esserci quella anomala. Ne prendiamo TRE di loro e le mettiamo su un piatto della bilancia. Sull'altro piatto ne mettiamo TRE della categoria N, ossia sicuramente normali (SECONDA PESATA).
(1a) Se la bilancia resta ancora in equilibrio la pallina anomala non può che essere quella lasciata ancora da parte. Ci resta, tuttavia, da scoprire se è più pesante o più leggera . La pesiamo insieme a UNA N e vediamo se è più pesante o più leggera. (TERZA PESATA).
(1b) Se la bilancia pende dalla parte delle S, siamo sicuri che la pallina anomala é PIU PESANTE, ma sta sempre nel trio delle S, diventate sospette pesanti P (rosse). L'ultima pesata, tra due di loro, completa la soluzione (TERZA PESATA). Se, infatti, la bilancia resta in equilibrio la pallina anomala è quella rimasta da parte e già sappiamo che è rossa. Se, invece, la bilancia pende da una parte, la pallina anomala è quella che sta nel piatto più in basso e deve essere, ovviamente, rossa.
(1c) Se invece la bilancia pende dalla parte delle N, siamo sicuri che la pallina anomala è PIU' LEGGERA, ossia diventa sicuramente blu, e sta nel trio delle S che diventano blu, ossia sospette leggere L. Ne prendiamo due di queste e ne mettiamo una su un piatto e una sull'altro (TERZA PESATA). Se la bilancia resta in equilibrio la pallina anomala è quella rimasta da parte e già sappiamo che è blu. Se la bilancia pende da una parte, la pallina anomala è quella che sta nel piatto rimasto più in alto, e deve sempre essere, ovviamente, blu.
N.B.: Nel caso (1a) la terza pesata serve soltanto a stabilire il peso della pallina il cui colore (peso) è già stato identificato nella seconda pesata. Nei casi (1b) e (1c) la terza pesata serve a stabilire qual è la pallina anomala, di cui si sa già il colore, ossia se è più pesante o più leggera.
Concludendo, nel caso (1) sono SEMPRE sufficienti TRE PESATE
Riportiamo lo schema di Fig. 1 per riassumere il caso (1) con le sue varianti.
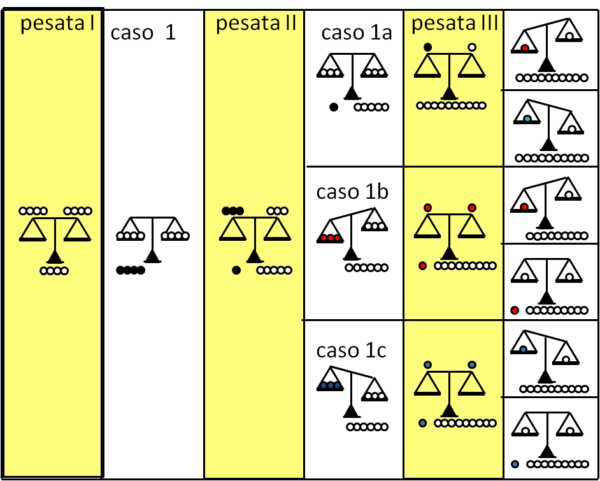
CASO (2)
Passiamo al caso (2), ossia a quello in cui la bilancia non sia in equilibrio, ma penda da un lato. La situazione resta ambigua, anche se fa diventare sicuramente bianche le quattro palline non messe sulla bilancia. Tuttavia, le quattro palline che sono più pesanti diventano rosse, mentre le quattro più leggere diventano blu: entrambe, infatti possono contenere la pallina anomala. La faccenda si complica un po' e la seconda pesata diventa fondamentale.
Per la SECONDA PESATA agiamo come segue: su un piatto mettiamo due sospette leggere (blu) e una sospetta pesante (rossa). Sull'altro piatto le due rimanenti sospette leggere (blu) e una sicuramente normale (bianca). In altre parole: su un piatto due blu e una rossa e sull'altra due blu e una bianca.
Le possibilità sono nuovamente tre: la bilancia resta in equilibrio (2a), scende dalla parte delle due blu e una rossa (2b) o, infine, fa il viceversa, ossia scende dalla parte delle due blu e una bianca (2c).
(2a)
La bilancia è in equilibrio, il che vuol dire che tutte e QUATTRO le palline supposte leggere diventano del tutto normali, ma lo fa anche quella supposta pesante. Rimangono in ballo tre palline sicuramente PESANTI (rosse). Per la TERZA PESATA, basta, allora, metterne una su un piatto e una sull'altro. Se la bilancia è ancora in equilibrio, la pallina rossa anomala è quella rimasta a terra. Altrimenti, è quella che fa pendere la bilancia dalla sua parte.
(2b)
Vi sono due alternative o la pallina rossa è quella anomala e fa pendere la bilancia dalla sua parte o una pallina blu delle due che stanno con quella bianca è quella anomala. E' necessaria una TERZA PESATA che risolva completamente l'ambiguità. Beh, non è poi così difficile! Basta mettere, ciascuna su un piatto, le due palline blu ancora sospette e le possibilità che rimangono risolvono il tutto: se le due palline restano in equilibrio, l'anomala è sicuramente quella rossa. Se invece una delle due fa pendere il piatto dalla sua parte, si conclude che l'anomala deve essere l'altra, dato che per le palline blu l'anomalia vuole dire essere più leggera.
(2c)
Esso è nettamente più semplice. La pallina rossa viene esclusa (se fosse stata anomala, avrebbe fatto pendere la bilancia dalla sua parte) e la pallina anomala può essere solo tra le due blu che stavano nel piatto insieme a lei. A questo punto la TERZA PESATA è banale: basta mettere queste due palline, ognuna su un piatto, e quella che sale verso l'alto è sicuramente la pallina anomala!
Riportiamo la Fig. 2 per riassumere e visualizzare l'intera faccenda.
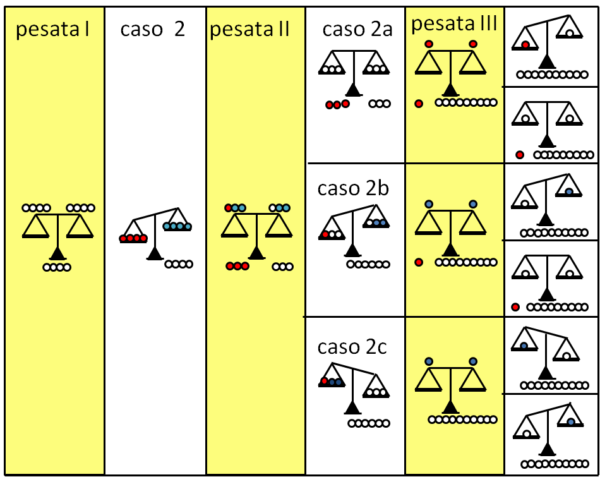
Ed eccoci alla seconda pesata. Mettiamo su un piatto due palline sospette leggere, insieme a una delle sospette rosse, mentre le altre due sospette blu le mettiamo sull'altro piatto insieme a una normale bianca.
Vi sono tre possibilità. La prima (2a) è che la bilancia stia in equilibrio. Il che vuol dire che il primo sbilanciamento era dovuto a una delle due palline rosse messe da parte. E' banale risolvere il problema pesandole una con l'altra (terza pesata). La seconda (2b) è quella in cui la bilancia pende dalla parte della unica rossa. Vi è una chiara ambiguità, dato che il risultato della pesata può dipendere sia dalle due blu che dalla rossa. Nessun problema, però... Pesiamo tra loro queste due sospette blu (terza pesata): se restano in equilibrio l'anomala è quella rossa messa da parte. Se invece vi è uno sbilanciamento l'anomala è quella blu il cui piatto resta più sollevato dell'altro. La terza (2c) è di nuovo molto semplice, dovendo solo pesare le due blu sospette tra loro (terza pesata): la bilancia, infatti, si solleva dalla parte della pallina rossa, la quale deve, perciò, essere sicuramente normale. L'anomala deve trovarsi tra le due blu che l'accompagnavano. Basta nuovamente pesarle tra loro per scoprire la più leggera, ossia quella anomala.
In conclusione (anche se volendo si possono adottare strategie diverse) la soluzione è UNICA: sono sufficienti TRE PESATE.
QUI il quiz





