Categorie: Fisica classica
Tags: relatività galileiana sistemi di riferimento urto anelastico urto elastico
Scritto da: Vincenzo Zappalà
Commenti:4
Attenti al treno **
Questo articolo è una delle tante "ciliegine cosmiche" che potete gustare QUI
Un'altra ciliegina nata durante uno scambio di commenti con Alberto parlando di effetto fionda. La faccenda si era risolta, ma penso non sia male trasformarla in uno dei saporiti frutti sotto spirito...
Il problema riguarda la fisica classica e, in particolare, gli urti elastici. Per cercare di renderlo il più semplice possibile, senza alcuna formula a rompere le scatole, affrontiamolo facendo ricorso ai soliti sistemi di riferimento e utilizzando, ancora una volta, un treno e una pallina (perfettamente elastica).
Cominciamo con la Fig. 1, un vero classico galileiano: un treno che viaggia a forte velocità e un'automobile parcheggiata a fianco della linea ferroviaria. Con lo sfondo giallo tratteremo i fenomeni visti dal sistema di riferimento del treno e con lo sfondo azzurro quelli relativi al sistema di riferimento della stazione o di un osservatore che assiste alla scena da fuori.
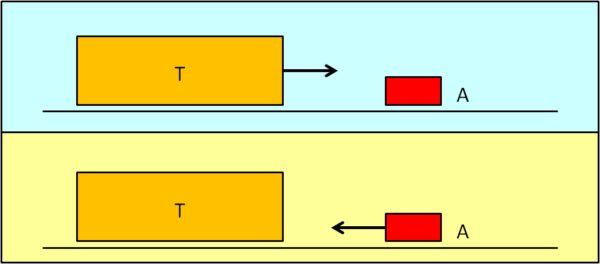
Il treno viaggia a velocità v1 e questo è quello che si vede nella vignetta azzurra in alto. Tuttavia, chi viaggia sul treno (vignetta gialla) si sente fermo e vede l'automobile venire incontro al treno con velocità uguale e contraria a quella del treno. Una vera banalità...
In Fig. 2 facciamo muovere anche l'automobile con una velocità v2. in verso contrario a quello del treno (vignetta azzurra). Cosa vede l'osservatore sul treno? Ovviamente si sente fermo e vede la macchina venirgli incontro, Tuttavia la macchina sta andando veramente incontro al treno con velocità v2. Ragione per cui chi sta sul treno vede la macchina venirgli incontro con velocità pari a v1 + v2.
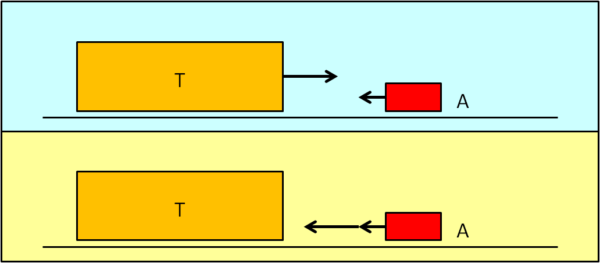
Anche questa è una vera banalità ...
Se, però, l'automobile stesse viaggiando proprio sui binari, la banalità si trasformerebbe in tragedia. Considerando un urto completamente anelastico, vedremmo in entrambi i casi il treno proseguire (magari rallentando un po') e trascinare con sé i rottami dell'automobile.
Fortunatamente, abbiamo a che fare con una pallina perfettamente elastica e la conclusione è soltanto divertente e non drammatica. Portiamoci, allora, in Fig. 3. La pallina è ferma sui binari. Tutto capita come prima, ma questa volta a seguito dell'urto vi è un perfetto rimbalzo della pallina.
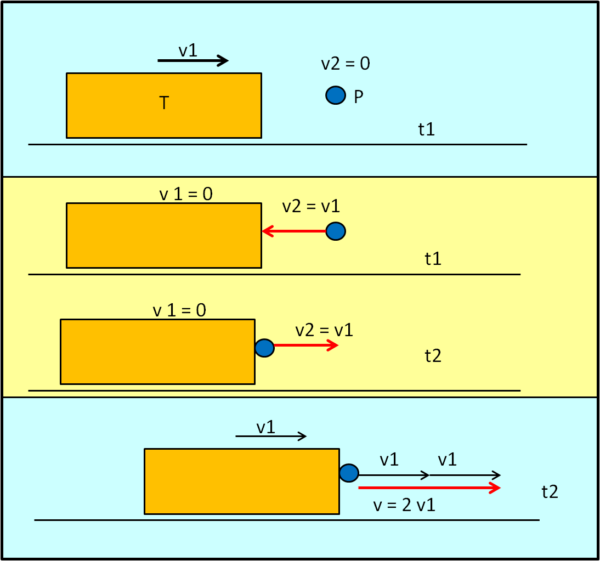
A quale velocità rimbalza? Beh ... semplice: nel sistema di riferimento del treno, essa arriva (t1) con velocità uguale a v1 e quindi rimbalza (t2) con una velocità uguale e contraria. Se, ci portiamo nel sistema azzurro, vedremo la pallina muoversi con velocità v1 verso destra (come appena dimostrato), ma a questa va aggiunta anche la velocità del treno, per noi fermi nella stazione, e quindi la pallina viene vista andare verso destra a velocità
v = 2v1
Infine, il caso che più c'interessa e che è facilmente deducibile da quello precedente (Fig. 4).
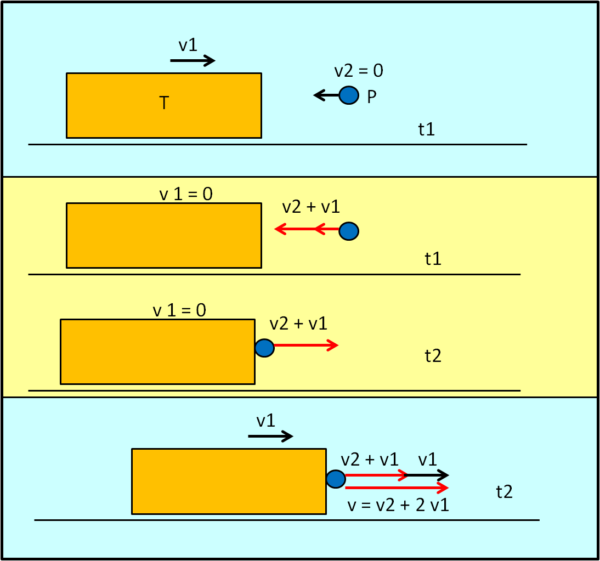
La pallina viaggia verso il treno a velocità v2. Il treno viaggia verso di lei a velocità v1. Nel sistema treno la pallina viaggia a una velocità v1 + v2. Nello stesso sistema essa rimbalza con velocità v1 + v2. Nel sistema stazione a questa velocità va aggiunta quella del sistema treno, ossia v1. Ne segue che la pallina viaggia, nel sistema stazione, alla velocità
v = v1 + v2 + v1 = 2v1 + v2
E' proprio vero... una ciliegina tira l'altra (e grazie ad Alberto per averla stimolata!)!






4 commenti
Refuso Ultima riga =2V1+V2
grazie Giorgino! Ah... se non ci foste voi!!!
E' solo per dimostrarti con quale attenzione ti seguiamo!
e io vi ringrazio ...