Questo articolo è inserito nella sezione d'archivio dedicata all'Elettromagnetismo

 

Forza e coraggio... iniziamo il nostro cammino verso le equazioni di Maxwell prima, e verso il campo elettromagnetico poi. Un percorso abbastanza lungo, ma che è stato fondamentale sia per le applicazioni tecniche e pratiche, che dominano il mondo attuale, sia per la formulazione della Relatività di Einstein. L'intera trattazione può ancora essere modificata qualora creasse difficoltà superabili. Vi invito, perciò, ad aiutarmi nelle eventuali migliorie. L'argomento è troppo importante per non cercare di renderlo il più comprensibile possibile. Buon viaggio!

1. Premessa

La prima parte di questo progetto vuol dare solo una visione quanto più generale possibile degli operatori che entrano in gioco per definire le equazioni di Maxwell. Come detto, Maxwell ha poi, in pratica, creato la sua teoria unificando  leggi già stabilite sia per il campo elettrico che magnetico concludendo, e qui sta la grande genialità, che essi erano due campi strettamente collegati che non potevano essere realmente trattati separatamente. Essi erano profondamente uniti e davano luogo a quello che oggi chiamiamo senza paura campo elettromagnetico. Un campo che si propaga anche nel vuoto attraverso onde che portano informazione senza alcun bisogno di movimento di materia. Una vera rivoluzione e, quindi, un devotissimo omaggio a Maxwell.

Tuttavia, mi preme anche ricordare un qualcosa, sicuramente sconosciuto a molti. Così come sono espresse oggi le equazioni di Maxwell sono solo quattro, ma restano indubbiamente una bestia nera per molti studenti e non solo.

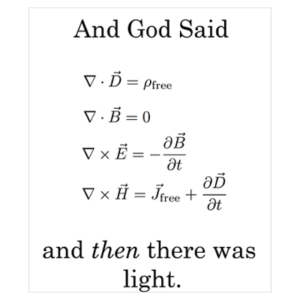
Beh... le vere equazioni di Maxwell sarebbe state ben più che una semplice bestia nera, ma addirittura un terribile tirannosauro nero, se non fosse intervenuto un genio quasi sconosciuto che è riuscito  a condensare le 20 equazioni in 20 variabili originali  in solo quattro equazioni in quattro variabili. Oltre ai nomi di Gauss, Ampere, Faraday e del sommo Maxwell, è doveroso ricordare, perciò, anche Oliver Heaviside che , in fondo, ci permette di affrontare con buona speranza di riuscita questo argomento. Lasciamo, come ormai prassi normale, il racconto, in parte triste, della vita di questo genio sconosciuto e incompreso alla nostra "storica" Daniela, e noi affrontiamo pure le equazioni di Maxwell come Oliver le ha sintetizzate.

 

2. Due forme e un  solo significato

Le equazioni di Maxwell possono essere descritte in due modi apparentemente diversi. Un modo può essere definito come LOCALE o DIFFERENZIALE e descrive ciò che capita nell'intorno di un singolo punto del campo, l'altro può essere definito come GENERALE o INTEGRALE e viene applicato a superfici e/o volumi di dimensioni qualsiasi. Ovviamente, uno si basa su equazioni differenziali  e l'altro su equazioni in cui la fanno da padroni gli integrali. Come è giusto che sia, è possibile passare da una formulazione all'altra attraverso dei teoremi appositi. Nei libri e nei media si usano entrambe, senza dare spesso l'informazione su questa diversa scrittura e portando spesso a confusioni e fraintendimenti.

Noi preferiamo seguire la strada "integrale" che, apparentemente, sembra diversa da quella per cui stiamo per introdurre  degli operatori che sembrano lavorare proprio sui differenziali. Perché lo facciamo? La risposta è multipla: innanzitutto perché gli operatori ci permettono di avere una prima idea concettuale sullo scopo finale delle equazioni di Maxwell, rimanendo a livello qualitativo. Insomma, capire i concetti base. Poi, perché il metodo integrale è decisamente più intuitivo soprattutto per le due ultime equazioni di Maxwell. Infine, perché lavorando in tal modo, potremo introdurre un paio di teoremi (uno è proprio richiamato in un capitolo della Relatività Generale al microscopio) che ci riporteranno alla simbologia descritta nel primo capitolo. Avremmo così a disposizione entrambi gli approcci.

Una scelta molto personale, ma che ho giudicato la via più "semplice" (magari sbagliando...). In certi momenti, la trattazione apparirà ai matematici più sofisticati un pochino "rozza", ma vi posso assicurare che alla fine otterremmo una descrizione completa e precisa sia dei concetti che della loro formulazione. A volte sarò forse perfino pedante nelle spiegazioni e chiedo pazienza ai più bravi, ma quando si decide di fare una cosa è giusto renderla comprensibile pienamente  al maggior numero di persone volenterose di imparare. Lo abbiamo fatto sia per la relatività che per la meccanica quantistica e quindi è più che giusto farlo per l'elettromagnetismo.

Come già detto, però, prima di iniziare a costruire le equazioni di Maxwell è necessario introdurre dei nuovi operatori che agiscono  sui vettori, dato che abbiamo proprio a che fare con campi vettoriali. Questi operatori saranno fondamentali nella trattazione differenziale. E' necessario, però  definirli al meglio fin dall'inizio, come preambolo di tutto ciò che seguirà. Oltretutto, alcune definizioni serviranno, forse, a chiarire ancora meglio certi concetti affrontati a livello un po' più alto nella Relatività Generale al Microscopio (RGM).

3. Campo vettoriale

Iniziamo col definire un campo vettoriale. Consideriamo uno spazio euclideo in tre dimensioni e definiamo su di esso un sistema di coordinate (vanno benissimo quelle cartesiane x , y e z) in modo da poter identificare in modo univoco  ogni punto del nostro spazio. Attenzione, adesso, a non confonderci... ad ogni punto dello spazio associamo un vettore. Questo vettore può rappresentare qualsiasi cosa. Potrebbe essere benissimo la velocità con cui un certo punto si muove rispetto al tempo, ma potrebbe essere il valore dell'altezza di quel punto rispetto al piano (in questo caso sarebbe un campo scalare), oppure una certa forza che agisce su quel punto.

Ad esempio, se consideriamo due punti-massa nel piano e seguiamo la legge di Newton, possiamo rappresentare la forza gravitazionale punto per punto o, ancora meglio, il campo gravitazionale. Qual è la differenza tra di loro? Poca cosa, il campo gravitazionale si ottiene dividendo la forza per la massa che subisce il campo, in modo da renderlo indipendente dalla massa che lo sta subendo. In poche parole, il campo vettoriale è un qualcosa che viene associato a un qualsiasi punto, e che caratterizza la forza per massa unitaria. A titolo di esempio, la forza gravitazionale data da GMm/r² diventa campo gravitazionale ponendo m = 1 (ovvero dividendo la forza per m).

Tuttavia, i campi vettoriali possono essere ben diversi. Ad esempio pensiamo all'acqua che scorre in un fiume  o alla stessa circolazione dell'aria nell'atmosfera. Se a ogni punto associamo la temperatura o la pressione siamo di fronte a un campo scalare. Se invece associamo la velocità che avrebbe un massa unitaria posta in quel punto avremmo un campo vettoriale. Fondamentale, però, è che resteremo  sempre e comunque nella fisica classica.

Altri tipi di campo sono quelli dovuti alla forza elettrica  e al magnetismo. Quello sarà proprio lo scopo di tutta la nostra trattazione. Tuttavia, per definire gli operatori che agiscono su un campo, possiamo, per il momento pensare a un fluido che scorre e il nostro campo vettoriale può comunque essere più o meno complicato.

Notiamo bene un altro punto importante: per adesso stiamo descrivendo il campo a un certo istante, ossia non stiamo tenendo conto della variazione del campo con il tempo. Questo importante fattore entrerà in gioco più avanti. per adesso occupiamoci della descrizione puramente geometrica dei nostri operatori.

Il primo operatore lo conosce molto bene chi ha seguito la RGM, ma non ci vuole molto a definirlo in modo generale e semplice.

3.1 Gradiente

Consideriamo una funzione qualsiasi di x, y e z (f(x,y,z)), che rappresenti una certa grandezza fisica . Si definisce gradiente  il vettore, indicato con grad (f), dato dalla somma delle tre derivate parziali prime della funzione lungo le tre direzioni, identificate attraverso i tre versori che identificano gli assi cartesiani.  Bene, ciò equivale a costruire un vettore in quel punto che abbia come componenti proprio le variazioni della funzione in un intervallino dx, dy e dz. Dato che la funzione è funzione di tre variabili, le differenze diventano delle derivate parziali (ossia derivate della funzione rispetto alla sola x, considerando y e z come costanti,  derivata della funzione rispetto alla sola y, e derivata rispetto alla sola z). Costruiamo perciò le derivate ∂f/∂x e ∂f/∂y e ∂f/∂z. A questo punto si può costruire un vettore, applicato nel punto, che abbia come componenti secondo gli assi x e y e z (di versori i, j e k) proprio queste derivate, ossia:

grad(f) = (∂f/∂x)i + (∂f/∂y)j + (∂f/∂z)k

In parole molto semplici, a partire da una funzione (scalare) abbiamo costruito un vettore, ossia abbiamo introdotto un campo vettoriale. nello spazio x, y e z.

Il gradiente non ci sarà molto utile, dato che noi partiremo già con un campo vettoriale, ma è meglio inquadralo perfettamente, soprattutto con il simbolismo che si porta dietro e che spesso spaventa soltanto a vederlo... Il simbolo, che chi ha letto la RGM già conosce, è il triangolo isoscele rovesciato, ossia il delta maiuscolo rovesciato:

∇

Se mi permettete, per evitare confusioni o dimenticanze di punti e puntini vari, io continuo a scriverlo nella vecchia maniera, ossia grad.

Qualsiasi sia il simbolo che volete usare il gradiente è, comunque, un'operatore che trasforma una funzione in un campo vettoriale.

3.2 Divergenza

Passiamo ora alla seconda operazione, la DIVERGENZA, decisamente più importante per i nostri scopi. La parola dà già un'idea del concetto che stiamo per affrontare. Esso è un operatore che ci indica quanto un campo vettoriale diverga da un certo punto. Il simbolo comunemente usato oggi  è dato dall'operatore gradiente seguito da il segno che indica un  prodotto scalare tra vettori:

∇ •       oppure  ∇ x (vecchio simbolo)

Il significato è abbastanza chiaro: il simbolo ∇ ci indica che stiamo operando su un vettore e il segno di prodotto scalare ci indica che tutto ciò deve essere applicato a un altro vettore. Vedremo che uno di questi è proprio quello che definisce il campo vettoriale e l'altro è il solito versore di componenti unitarie che definisce gli assi cartesiani di riferimento. In modo molto rozzo, potremmo dire che è il contrario del gradiente, in quanto la divergenza trasforma un campo vettoriale in uno scalare (il prodotto scalare di due vettori è uno scalare, è descritto esaurientemente QUI).

Noi, però non amiamo tanto questo simbolismo che rischia di aggiungere confusione e preferiamo indicare l'operatore divergenza con il simbolo "antico", ossia div. Ne segue che ci troveremo di fronte a una scritta:

div(u) = k

Dove u è il vettore del campo e il risultato è uno scalare numerico che viene associato al punto in questione.

Possiamo fermarci qui? Eh no! me la sarei cavata troppo in fretta ed è meglio andare molto più a fondo e usare rappresentazioni adatte a comprendere perfettamente con cosa abbiamo a che fare...

Immaginiamo, allora, che il nostro punto sia rappresentato da un piccolissimo cubo di volume  dV = dx dy dz

Per chiarire meglio le idee, in modo pratico, immaginiamo anche che il campo vettoriale u rappresenti la velocità con cui si muove un fluido. Possiamo allora dire che:

Se la divergenza è positiva vuol dire che il fluido esce con velocità maggiore dal nostro cubetto rispetto a quella con cui vi entra. La divergenza è invece negativa se avviene il contrario. Ovviamente, essa sarà uguale a zero se la velocità rimane costante sia in entrata che in uscita (attenzione: stiamo parlando di variazione di un campo in relazione alla posizione del punto (ossia del cubetto) e non ancora della variazione del campo rispetto al tempo!).

Consideriamo la Fig. 1.

Immaginiamo che il fluido scorra solo parallelamente all'asse x. Le facce del cubo coinvolte dal flusso sono solo dAx₁ e dAx₂.  Il vettore del campo sia quindi u = u_x. esso varia da punto a punto, ma può tranquillamente essere applicato al centro delle facce quadrate, ortogonali all'asse x. Avremmo, perciò, un vettore u_x1 che entra in dAx₁ e un vettore u_x2 che esce da dAx₂.  Basta un'occhiata per dire che la velocità del fluido entrante è minore della velocità del fluido uscente, il che comporta una divergenza POSITIVA, per quanto definito prima. Ovviamente, se avessimo invertito il verso del fluido, avremmo concluso il contrario, ossia il vettore che "entra"  (u_x2) sarebbe maggiore di quello che "esce" (u_x1).

Vediamo di generalizzare e quantificare la situazione, considerando un'operazione ben conosciuta che agisce sui vettori: il prodotto scalare. Sappiamo bene che essa agisce sui vettori e dà come risultato un valore scalare. Ricordandola

v1 x v2 = v1 v2 cos (α)      dove α è l'angolo tra i due vettori

Nel nostro caso, possiamo prendere come vettore v1 il vettore del campo (u) e come vettore v2 il versore relativo all'asse x (i) che ESCE dalla faccia (in altre parole al posto dell'area dAx₁ consideriamo il versore ad essa perpendicolare). Per la faccia dAx1 l'angolo α è uguale a zero, u_x1 è proprio il vettore che entra, mentre il versore, sempre unitario,  ha come segno il segno meno, dato che va in verso opposto al versore che indica l'asse x (i). Il prodotto scalare, perciò, è  dato solo dal prodotto tra u_x1 e - i. La componete di  -i  vale -1 e, quindi, il prodotto scalare è dato da

u_x1 x -i =  -u_x1 i = - u_x1

Spostiamoci sulla faccia dAx₂. L'angolo è sempre uguale a zero e  il prodotto scalare diventa, adesso:

u_x2 x i = u_x2                    (il versore vale adesso i, dato che va nel verso delle x crescenti)

Le altre facce non sono coinvolte e quindi possiamo sommare i due prodotti scalari ottenendo:

- u_x1 + u_x2 > 0.

In poche parole, otteniamo un valore numerico che risulta POSITIVO.

Se invertissimo il senso del campo vettoriale, otterremmo invece:

- u_x2 x i = - ux2

- u_x1 x - i = ux1

Sommando avremmo:

- u_x2 + u_x1 < 0

Ossia otterremmo proprio un valore NEGATIVO.

Ovviamente, se il vettore uscente e quello entrante fossero stati uguali (ossia velocità del fluido costante) avremmo avuto come risultato ZERO. La stessa cosa sarebbe successa se il flusso fosse stato parallelo solo all'asse y o all'asse z.

N.B.: Quando si ha una fluido che scorre e la velocità d'entrata e uguale a quella d'uscita, la divergenza è zero. In termini pratici diremmo che il fluido é incomprimibile.

Generalizziamo ancora di più e prendiamo un campo comunque orientato, ad esempio un campo vettoriale che sia sempre perpendicolare all'asse z. Disegniamo la Fig. 2.

Ne segue che le due facce del volumetto dA_z1 e dA_z2 non verrebbero coinvolte nel flusso, ma  lo sarebbero sia dA_x1 che dA_x2 e, anche, sia dA_y1 che dA_y2. Come quantificare questi effetti separatamente? Facilissimo!  Basta considerare il nostro vettore u₁ (entrante) separato nelle sue due componenti u_x1 e u_y1. Ognuna di loro risulta parallela al versore uscente dalla faccia corrispondente e quindi basta  calcolare sia i prodotti scalari di u_x1 e u_x2 con il versore uscente da dA_x1 e dA_x2, ma anche i prodotti scalari tra u_y1 e u_y2 e i versori uscenti da dA_y1 e dA_y2, rispettivamente.  Poi basterebbe sommare tutti e quattro i prodotti scalari e otterremmo la stessa cosa che abbiamo ottenuto nel caso più semplice: se la somma fosse positiva il campo vettoriale uscente sarebbe maggiore di quello entrante e viceversa.

Non ci vuole molta fantasia a considerare  un campo che influisca anche sulle facce dA_z1 e dA_z2. In conclusione l'operazione divergenza non è altro che uno scalare corrispondente alla somma dei sei prodotti scalari. Tuttavia, ricordiamo che il nostro cubetto è infinitesimo e quindi la differenza tra u_x2 e u_x1, ad esempio, è anch'essa infinitesima. Questa differenza è, però, solo quella relativa alle componenti del vettore u lungo x, che quindi diventa le derivata parziale di u_x rispetto a x. Analoga considerazione per le altre differenze. Ne segue che possiamo scrivere il nostro operatore come:

div(u) = (∂u_x/∂x) + (∂u_y/∂y)+ (∂u_z/∂z)

In poche parole, possiamo anche considerare la faccenda nel modo seguente:

Consideriamo due vettori, il primo è rappresentato da

u = (∂u_x/∂x)i + (∂u_y/∂y)j + (∂u_z/∂z)k       (notate l'uguaglianza tra le componenti di questo vettore e quelle del vettore gradiente)

Il secondo da

s = i + j + k

Ma  il prodotto scalare tra due vettori è dato proprio da uno scalare che è la somma dei prodotti scalari delle componenti dei due vettori (si può anche dimostrare formalmente, ma la relazione è estremamente ovvia)

u x s = (∂u_x/∂x)i x i + (∂u_y/∂y)j x j+ (∂u_z/∂z)k x k =

u x s = (∂u_x/∂x) + (∂u_y/∂y)+ (∂u_z/∂z) = div (v)

Insomma, scegliete il metodo che più vi piace, dato che, in realtà, sono sempre la stessa cosa e definiscono il concetto di divergenza, ossia l'entità del campo vettoriale uscente da un volumetto infinitesimo, preso con il suo segno: se è > o è maggiore il campo che esce, se è < 0 è maggiore il campo che entra. Se è uguale a zero, il campo rimane costante spazialmente.

Riassumendo:

Il gradiente, attraverso le differenze di una funzione nei dintorni di un punto, è un operatore che associa queste variazioni alle componenti di un vettore.

La divergenza esegue un prodotto scalare tra questo vettore e quello del versore del sistema di riferimento.

N.B.: in termini più professionali, la mia trattazione potrebbe apparire un po' rozza e anche ripetitiva, ma le conclusioni sono esattamente le stesse e quindi ben venga la... semplicità (spero).

3.3 Rotore

Introduciamo un nuovo operatore, capace, questa volta, di valutare quanto un campo vettoriale sia in grado di causare una rotazione in un certo punto del campo. Useremo, per analogia con quanto fatto per la divergenza, un cubetto con dV = dx dy dz.

L'operatore rotore viene indicato normalmente con il simbolo:

∇ x      oppure  ∇ ∧ (vecchio simbolo)

noi useremo, però, il vecchio simbolo (molto più esplicativo e meno "terrificante ") di  rot

Il simbolo ∇ ci indica che stiamo operando su un vettore e il segno di prodotto vettoriale ci indica che tutto ciò deve essere applicato a un altro vettore (esattamente come la divergenza), ma questa volta il risultato deve essere ancora un vettore, in quanto sappiamo bene  che il prodotto vettoriale identifica un nuovo vettore che segue la celebre regola della mano destra o della vite come esaurientemente spiegato QUI (da poco prima della Fig. 15 in poi).

In parole povere, se la divergenza ci diceva se nel nostro volumetto corrispondente a un certo punto entra o usciva un'entità maggiore o minore di campo vettoriale, adesso siamo interessati a vedere se il campo vettoriale è in grado di impartire una rotazione al nostro cubetto. Come prima, utilizziamo come campo vettoriale la velocità di un fluido.

N.B.: in termini più pratici, il rotore ci indica se siamo in presenza di un vortice, ossia una rotazione del fluido attorno al nostro punto.

Ormai abbiamo imparato molto dalla trattazione elementare della divergenza e possiamo tranquillamente scrivere una variazione di un certo vettore in una certa direzione come la sua derivata parziale lungo questa direzione, evitando così differenze e rapporti di differenze che alla fine potrebbero anche rendere inutilmente lunghi e monotoni certi passaggi. Passiamo decisamente alla Fig. 3a.

Il campo vettoriale che investe il nostro volumetto agisca, per semplicità, nel piano x,y, perpendicolare a z. Ciò vuol dire, nuovamente, che trascuriamo le due facce perpendicolari all'azze z. Beh... è immediato intuire che lo spigolo in alto a sinistra del cubetto subisce un vettore del campo che è maggiore di quello dello spigolo in basso a sinistra. Ciò implica una ROTAZIONE del cubetto (nel caso della figura in senso ORARIO).

Entriamo nei dettagli... Questa volta il campo entrante o uscente può tranquillamente rimanere costante, ma esiste invece una variazione di esso al variare della posizione lungo l'asse y. Ciò vuol dire, in pratica, che per una variazione di y nel verso crescente (positivo) corrisponde una variazione  crescente della componente u_x del vettore u. In parole contratte, possiamo concludere che:

∂u_x/∂y > 0              (la derivata è parziale, dato che u_x è funzione sia x che di y)

Siamo proprio di fronte a un prodotto vettoriale in cui i vettori coinvolti sono quello che indica la componente di un versore lungo y (j) e quello che indica la componente u_x. Sappiamo molto bene che il prodotto vettoriale di due vettori tra loro perpendicolari da luogo a un vettore che ha per modulo il prodotto dei moduli e per direzione un'asse ortogonale al piano dei primi due (ossia  l'asse z). Il suo verso segue quello della mano destra, ossia se l'indice indica il primo vettore e il medio il secondo vettore, il verso del  vettore prodotto vettoriale segue il pollice. O, se preferite, la rotazione di una vite in senso orario indica che la vite sta entrando, ossia che il verso finale è entrante nel foglio.

Siamo soddisfatti? No, non ancora, dato che lo stesso tipo di rotazione può essere ottenuta imponendo un campo vettoriale avente la direzione parallela all'asse y, decrescente però nel verso delle x crescenti (Fig. 3b). In particolare, per una variazione di x nel verso crescente (positivo) si ottiene una variazione decrescente del vettore u_y. In questo caso si ha, ovviamente, che:

∂u_y/∂x < 0

anche questa rotazione, ovviamente, è indicata da un vettore lungo l'asse z avente lo stesso verso di quella precedente

N.B.: Se avessimo applicato un campo verticale, diretto verso il basso, crescente per x crescente avremmo avuto lo stesso risultato, dato che la componente u_y sarebbe aumenta per x crescente, ma in verso opposto al versore j e quindi sarebbe risultata negativa rispetto alla direzione del versore diretto verso valori positivi.

In entrambi i casi abbiamo ottenuto una rotazione del cubetto in senso orario, Ne segue che la componente  del rotore nella direzione dell'asse z (il rotore è dato dal prodotto vettoriale!) è data dalla somma delle due componenti appena trovate, dato che esse  esauriscono le possibilità di ottenere la componente finale lungo l'asse z.

Indicando per comodità t il vettore rotore, la sua componente t_z è data da:

t_z = (∂u_x/∂y - ∂u_y/∂x)

Attenzione, però... Abbiamo anche trovato che questa componente indica una rotazione oraria, ossia con il vettore corrispondente che entra nel piano x,y, ossia nel verso opposto a quello del versore k. In altre parole, la componente nel verso positivo di k è -t_z, ossia:

- t_z = - (∂ux/∂y - ∂uy/∂x) = ∂uy/∂x - ∂ux/∂y

Ragionando in modo analogo per le altre due componenti del vettore rotore, esso , alla fine, assume l'espressione:

t = rot(u) = (∂uz/∂y - ∂uy/∂z) i + (∂ux/∂z - ∂uz/∂x) j + (∂uy/∂x - ∂ux/∂y) k

In pratica, abbiamo scritto proprio il vettore prodotto vettoriale, le cui componenti erano già state determinate QUI (formula (14) e appendice sulle matrici e determinanti che segue).

Bene... direi che, pur utilizzando un metodo molto semplice abbiamo ottenuto quanto volevamo, ossia definire compiutamente gli operatori gradiente, divergenza e rotore. Direi che, agendo in questo modo, abbiamo eliminato l'apparente complessità che si potrebbe avere di fronte alle equazioni differenziali di Maxwell.

A questo punto possiamo entrare decisamente all'interno dei campi vettoriali elettrico e magnetico e descrivere le loro relazioni. Gli operatori, che metteremo da parte, ci serviranno comunque, dato che li sfrutteremo qualitativamente per avere un'idea della situazione da un punto di vista geometrico. Poi, alla fine, li faremo entrare prepotentemente in campo.

Questo primo articolo è piuttosto lungo, ma ho preferito che riportasse i tre operatori in modo da poter fare confronti e digerirli molto bene. Fatto questo, i teoremi finali che ci permetteranno da passare dalla visione integrale a quella differenziale  non spaventeranno più nessuno...