Categorie: Cosmologia Storia della Scienza
Tags: Big Bang espansione Universo legge di Hubble Legge di Hubble-Lemaitre Lemaitre
Scritto da: Daniela
Commenti:11
Georges Lemaître: l'Uomo, il Genio, l'Umiltà
In attesa che il prof. rientri dalla breve vacanza, riproponiamo questo articolo (pubblicato il 10/11/2018), che farà parte di una nuova sezione d'archivio dedicata agli studiosi che hanno fornito contributi fondamentali, diretti o indiretti, all'architettura del pensiero relativistico. Questa nuova avventura è iniziata con Michael Faraday e Arthur Stanley Eddington.
Il presente articolo è stato inserito nelle pagine d'archivio:
"Quattro passi nella storia della Scienza", "Spaziotempo/Cosmologia" e "Einstein ha sempre ragione (o quasi)"
Prendete un sacerdote cosmologo che insegna Fisica all'Università, Albert Einstein, una formula molto famosa che non è E=mc2, un uovo cosmico, un papa e un mistero rimasto tale per ottant'anni. Frullate il tutto e non otterrete una barzelletta né un giallo di Agatha Christie, bensì la storia vera di Georges Lemaître, una delle menti più brillanti del XX secolo, rimasto fuori dai riflettori, quindi dalla conoscenza del grande pubblico, ma non meno importante di altri suoi famosi colleghi per l'enorme balzo in avanti che ha fatto fare alla conoscenza dell'Universo. Vediamo perché...
v = H0 d
v è la velocità di allontanamento, d è la distanza attuale e H0 si chiama Costante di Hubble, che del tutto costante non è in quanto varia continuamente in funzione del tempo; ma se la misuro in questo momento è davvero costante ed è valida in tutto l'Universo. Ma di quale tempo stiamo parlando? Semplice... quello che è trascorso dalla nascita dell'Universo e che, guarda caso, ci viene fornito da 1/Ho.
Il valore attribuito oggi alla Costante di Hubble è 67 Km/s/Mpc. Il che significa che per ogni Mpc (Megaparsec = 3,26 x 106 anni luce) di distanza, la velocità cresce di 67 Km/s. Tanto per fare un esempio: se una galassia che si trova a tre milioni di anni luce da noi, scappa via a 67 Km/s, un'altra che osserviamo a 300 milioni di anni luce da noi, si allontenerà a ben 6.700 km/s.
No, non stiamo dando i numeri: stiamo descrivendo, in modo estremamente sintetico ed in tutta la sua meravigliosa semplicità, la formula che esprime la Legge di Hubble, nella quale v rappresenta la cosiddetta velocità di recessione delle galassie e d la loro distanza dalla Terra. Se volete approfondirne la conoscenza, potete farlo grazie a QUESTO ARTICOLO e ai link in esso contenuti.
Tutto chiaro? Forse. Tutto esatto? Mica tanto... infatti quella legge non è più intitolata soltanto a Edwin Hubble, ma ha recentemente cambiato nome e dobbiamo abituarci a chiamarla LEGGE DI HUBBLE-LEMAITRE.
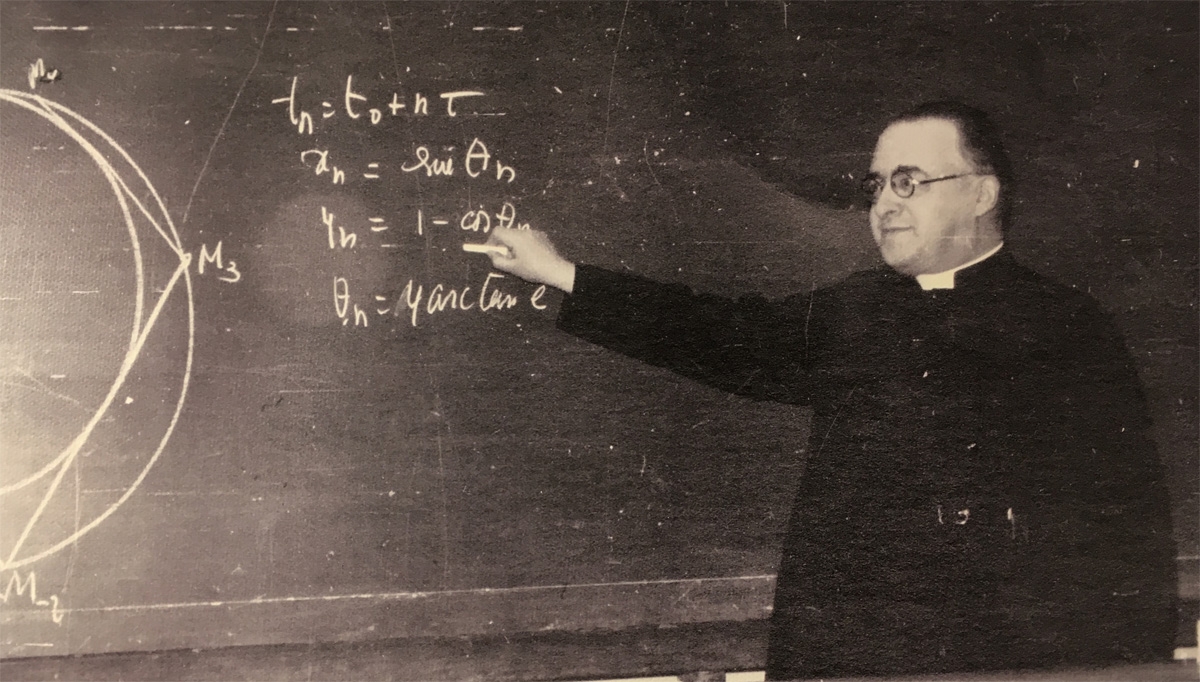
Fu, infatti, il sacerdote e astronomo belga Georges Lemaître il primo a teorizzare, nel 1927, l'espansione fisica dell'Universo e lo fece in un articolo dal titolo "Un Universo omogeneo a massa costante e raggio crescente spiega la velocità radiale delle nebulose extragalattiche"(*). Peccato che questo storico articolo sia stato pubblicato in una poco conosciuta rivista scientifica francese e che, a quei tempi, non esistesse internet... è per questo che le analoghe conclusioni che furono rese pubbliche (tramite canali più autorevoli e conosciuti) da Edwin Hubble nel 1929 sembrarono arrivare per prime. Se a questo aggiungiamo il fatto che nella traduzione in inglese dell'articolo di Lemaître, fatta nel 1931 da Sir Arthur Stanley Eddington (sì, proprio quel Eddington che fornì la prima prova sperimentale della Relatività Generale), scomparvero alcuni paragrafi essenziali per attribuire la paternità della scoperta al sacerdote belga, ci sono tutti gli elementi per pensare ad un'azione disonesta perpetrata nei suoi confronti.
Questa volta, però, la realtà ha superato la fantasia e il giallo è stato risolto nel 2011, grazie al ritrovamento (da parte di Mario Livio, astrofisico allo Space Telescope Science Institute a Baltimora, autore tra l'altro di un pregevole libro sulla sezione aurea) di una lettera nella quale lo stesso Lemaître spiega di essere stato lui a voler eliminare quei paragrafi in quanto, a suo parere, superati dalle successive osservazioni effettuate proprio da Hubble.
Insomma, nessun riconoscimento dolosamente negato (come, tanto per fare un esempio "a caso", il Nobel a Jocelyn Bell per la scoperta delle pulsar), ma un chiaro e rarissimo caso di «onestà intellettuale e modestia che hanno fatto preferire il progresso della Scienza alla visibilità personale». E' così che recita, infatti, la Risoluzione B4, con la quale tremila scienziati membri dell'Unione Astronomica Internazionale, riuniti a Vienna alla fine dello scorso mese di agosto, hanno votato il cambiamento del nome della Legge di Hubble in Legge di Hubble-Lemaître. La risoluzione è stata poi confermata definitivamente tramite referendum online al quale hanno avuto diritto di voto tutti i trentamila iscritti alla UAI. E, dopo quasi un secolo, si è finalmente dato a Cesar... ops... a Lemaître ciò che è di Lemaître!
Ma se questa vicenda vi fa pensare che il nostro Monsignore astrofisico fosse timido, umile e remissivo, vi sbagliate di grosso: egli era ben consapevole delle proprie capacità e non guardava in faccia a nessuno quando si trattava di esporre le idee di cui era (giustamente, come è stato in seguito verificato) convinto.
Non ci pensò due volte, infatti, a spiegare la sua teoria dell'UOVO COSMICO (successivamente ribattezzato, in modo dispregiativo, Big Bang da Fred Hoyle) ad Albert Einstein, convinto sostenitore dell'Universo statico, che gli rispose “I vostri calcoli sono esatti, ma la vostra fisica è abominevole”, salvo poi ammettere, molti anni dopo, che quello era stato il più grande errore della sua vita.
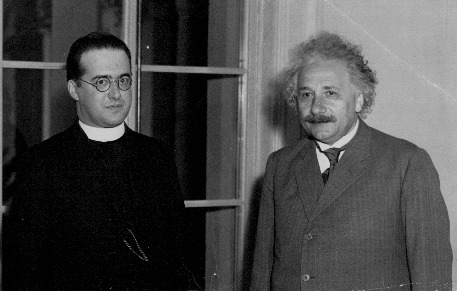
Come non ci pensò due volte a recarsi da papa Pio XII, che in alcuni discorsi pubblici aveva ipotizzato che il Big Bang potesse identificarsi con la creazione, per convincerlo a non farlo più, in quanto tale argomentazione avrebbe potuto dimostrarsi un'arma a doppio taglio per la Chiesa. Il papa ci rimase un po' male, ma gli diede ascolto e fece bene... oggi che si ipotizza anche un prima del Big Bang, quel consiglio appare più attuale e saggio che mai.

Ascoltiamo il racconto di questi due episodi dalla viva voce di Carlo Rovelli in questo gradevole video:
Insomma... gran bel personaggio questo Uomo di Scienza e di Fede che riuscì a vivere intensamente entrambe le sue passioni, senza che l'una pestasse i piedi all'altra. Un po' come aveva tentato di fare Galileo, profondamente credente e convinto che la Bibbia spiegasse "come si vadia al cielo, e non come vadia il cielo", però i tempi non erano ancora maturi e per poco non finì sul rogo... ma questa è un'altra storia e l'abbiamo raccontata QUI.
(*) Come spiegatoci da Fabrizio (QUI e QUI), il modello sviluppato da Lemaitre nel 1927 si basa sullo sviluppo fisico-matematico delle equazioni di campo di Einstein e spiega le osservazioni eseguite sull’allontanamento di 42 nebulose extragalattiche (è così che ai tempi erano chiamate le galassie) da Gustaf Strömberg nel 1925, sulla base dei dati ottenuti dall'osservatorio di Mount Wilson. La velocità di allontanamento risultava proporzionale alla distanza (come “certificato” due anni dopo da Hubble con la sua famosa legge), tuttavia il fattore di proporzionalità misurato all’epoca è poi risultato sovrastimato rispetto a quello che oggi consideriamo reale, per l'errore di misura delle distanze che si faceva all'epoca.
QUI parliamo di sir Arthur Stanley Eddington, uno dei più illustri astronomi del XX secolo, che, tra i tanti allievi, ebbe anche Georges Lemaître.





11 commenti
Dunque il tempo trascorso dalla nascita dell'universo lo si ricava da 1/H. Ammettiamo per approssimazione che H sia una vera costante, 1:67 = 0.0149... Sappiamo che il risultato dovrebbe essere circa 14 miliardi di anni... Ma mi perdo con le unità di misura di H... Km/s/Mpc...
perché mai Alberto...?
H = v/d --> km/(s km) = 1/sec
1/H = secondi (ossia tempo!)
Scusa, ma allora ve lo richiedo qui. Quando nel 1927 Lemaitre teorizzo' l'espansione dell'universo, in base a quali dati lo fece? Hubble aveva già rese note le sue osservazioni astronomiche sul redshift? Ho capito di no. O Lemaitre si baso' solo sulle equazioni di Einstein, ricalcolandole in qualche modo?
Da quello che ho capito io, sembra che l’idea di Lemaitre nasca da un’analisi puramente matematica delle equazioni della Relatività, non da dati derivanti da osservazioni.
Cercando un riscontro a questa informazione, ho appena scovato questo interessante articolo https://disf.org/einstein-cosmologia-lemaitre
Per quanto ho capito, c'è una relazione tra le osservazioni fatte sull'allontanamento delle galassie e l'articolo di Georges Lemaìtre del 1927. Lo dice lo stesso titolo dell'articolo: “Un universo omogeneo di massa costante e di raggio crescente che rende conto della velocità radiale di nebulose extragalattiche”.
Ciò non significa che il modello d'universo di Lemaìtre sia derivato dai dati delle osservazioni. Il modello credo sia uno sviluppo fisico-matematico delle equazioni di campo di Einstein. Questo modello spiega le osservazioni sull'allontanamento delle galassie fatte anche da Lemaìtre stesso. Infatti, nello stesso articolo, Lemaìtre riporta le misure fatte su 42 galassie osservando che si allontanano a velocità proporzionale alla distanza. In questo modo aticipava, almeno a detta di autori francesi, la legge (empirica) che Hubble pubblicherà nel 1929.
Il fattore di proporzionalità misurato da Lemaìtre e Hubble è molto sovrastimato per l'errore di misura delle distanze che si faceva all'epoca.
La fonte di queste informazioni è il libro di ]ean-Pierre Luminet "La segreta geometria del cosmo". Nonostante il titolo ad effetto, il libro è molto interessante.
Interessante davvero, Fabrizio, grazie!
Non so quanto possa essere impegnativo perchè non conosco quel libro, ma se tu avessi tempo e voglia di scriverne una sintesi divulgativa, sarebbe un importante contributo alla conoscenza di quel grande personaggio che è stato Lemaitre (oltre che un bel fiore all’occhiello per questo circolo-blog).
Correggo parzialmente quanto detto sopra. Andando alla fonte, nell'articolo del 1927 Lemaître analizza i dati di velocità radiale di nebulose extragalattiche (galassie) pubblicati da Gustaf Strömberg nel 1925 ottenuti dall'osservatorio di Mount Wilson e cita anche Hubble. Le osservazioni non sono state fatte direttamente da lui come riporta il libro che ho citato. Forse un errore di traduzione.
In risposta a Daniela, inserisco una sintesi dei contenuti del libro che ho citato che avevo preparato qualche anno fa per un forum di astronomia. Nel libro è citato spesso Lemaître, se non altro per orgoglio francofono. Tenete conto che il libro è precedente alla risoluzione dell'UAI che riconosce la paternità condivisa della legge di Hubble.
Il libro inizia con una domanda "Quale è la forma dello spazio?", intendendo qui spazio fisico. Nel libro non c'è una risposta univoca a questa domanda. Sono invece esaminate le possibili forme che lo spazio fisico potrebbe avere, definite dalle loro proprietà quali curvatura, dinamica temporale, estensione e topologia. E’ dato anche ampio spazio alle osservazioni astronomiche che potrebbero portare a restringere l'insieme delle possibili forme. Inoltre ci sono molte notizie storiche condite da un pizzico di polemica che vuole evidenziare il punto di vista francofono su alcune vicende e l’inopportuno sensazionalismo che spesso colora alcune notizie circolate in materia di cosmologia.
In questo percorso si incontrano numerosi argomenti di fisica e matematica esposti in modo divulgativo nei loro elementi essenziali, senza richiedere conoscenze matematiche e di fisica avanzate. Alcune parti più complesse probabilmente richiedono la pazienza di rileggerle più volte.
Ciò che caratterizza maggiormente questo libro è l’avere trattato in modo esteso le diverse topologie dello spazio andando oltre quelle più semplici normalmente assunte, implicitamente o esplicitamente. Non manca comunque una efficace esposizioni della relatività generale e dei modelli cosmologici da essa derivati che mettono in relazione proprietà dello spazio come la curvatura e la dinamica temporale con la densità di materia e di energia. In queste due ultime grandezze hanno un ruolo rilevante le ipotesi sulla materia oscura e l'energia del vuoto, che sono trattate in due specifici capitoli di approfondimento.
In conclusione della postfazione l’autore afferma che la questione della forma dello spazio al momento della stesura dal testo (2004) era ancora aperta. Non so se ci siano state evoluzioni significative dopo di allora.
Il percorso mi è parso comunque affascinante, anche se alla fine si scoprisse che lo spazio fisico su scala cosmologica è il buon vecchio spazio euclideo nella sua topologia più semplice.
Per chi volesse qualche dettaglio in più sugli argomenti trattati nel libro, riporto una sintesi del contenuto per come l’ho capito ed i capitoli nei quali è trattato.
La relatività generale (introdotta nei cap.5, 6 e 7) sotto le ipotesi semplificative di omogeneità e isotropia dello spazio, ipotesi riscontrabili su scale di qualche centinaio di milioni di anni luce, ha consentito di sviluppare numerosi modelli (cap.9 e 35). Alcuni hanno ora solo un interesse storico essendo in disaccordo con le osservazioni sperimentali, altri mantengono la loro validità.
Questi modelli collegano (cap.10 e 11) la curvatura dello spazio, euclideo/sferico/iperbolico, e la sua dinamica temporale, espansione/contrazione/stazionaria, con la densità di materia ed energia. Qui hanno un ruolo essenziale le ipotesi sulla materia oscura e l’energia del vuoto. A questi due argomenti sono dedicati due specifici capitoli di approfondimento (cap.37 e 36), quest'ultimo tratta anche la relazione tra energia del vuoto e la costante cosmologica con interessanti informazioni storiche sull’evoluzione di questa idea.
Le proprietà locali dello spazio trattate dalla relatività, curvatura e dinamica temporale, non esauriscono le proprietà dello spazio (cap.15). L’altro elemento è la topologia (introdotta nel cap.12) che, tra l’altro, insieme con la curvatura determina l’estensione finita/infinita dello spazio.
A identiche proprietà geometriche locali possono corrispondere più topologie. Usualmente questo aspetto è ignorato poiché, implicitamente o non, si considera la topologia più semplice (monoconnessa). In questo caso è il tipo di curvatura che definisce se lo spazio è finito o infinito: spazio euclideo e iperbolico -> infinito; spazio sferico -> finito.
Per topologie più complesse (multiconnesse; cap.12,13 e 14) le cose si complicano. In particolare si apre la possibilità di spazi finiti e illimitati anche euclidei e iperbolici, curvature che oggi sembrano essere le candidate più comunemente accettate per lo spazio fisico (prima di leggere questo libro avrei pensato che dire finito e illimitato fosse una contraddizione).
Per visualizzare queste affermazioni dobbiamo ricorrere ad esempi bidimensionali (cap.13). In due dimensioni uno spazio monoconnesso è il piano ed esempi di multiconnesso sono la superficie di una ciambella o quella di un cilindro. Un test per distinguerli è quello del cappio. Se faccio un cappio con una corda appoggiata sulla superficie e provo a stringerlo, se lo spazio è monoconnesso, riesco sempre a stringerlo completamente, se è multiconnesso non sempre arrivo a stringerlo totalmente. La superficie di un cilindro di lunghezza infinita (intesa come spazio bidimensionale multiconesso) è localmente piatta (sulla superficie di un cilindro vale il teorema di Pitagora, la somma degli angoli interni di un triangolo è 180°, ecc.), ma almeno in una direzione è finita: ci si può allontanare da un punto fino a un massimo, andando oltre ci si avvicina nuovamente arrivando dalla direzione opposta dalla quale si era partiti. Nel libro l'esempio è completato arrivando a identificare una superficie piatta e finita (toro piatto).
E’ sconsigliabile da questo cercare di visualizzare i corrispondenti tridimensionali poiché il nostro cervello si rifiuta e rischiamo di prendere notevoli abbagli.
Questa divagazione sulla topologia degli spazi multiconnessi può sembrare un’inutile aggiunta di ipotesi che nulla hanno a che vedere con lo spazio fisico e in contradizione con il principio di semplicità che fa preferire le teorie con minori ipotesi.
Nel cap.22 l’autore evidenzia come questa apparente aggiunta di complessità potrebbe trasformarsi in una semplificazione o una necessità a causa delle criticità che possono sorgere nel considerare spazi fisici infiniti. Un esempio portato è la relazione con i modelli di universi scaturiti spontaneamente dalle fluttuazioni del vuoto quantistico che, nei loro attuali limiti di affidabilità, farebbero preferire gli spazi di volume minore. Tra gli spazi euclidei o iperbolici, che oggi sembrano essere i candidati comunemente accettati per lo spazio fisico, sarebbero preferiti quelli multiconnessi essendo gli unici spazi finiti con questo tipo di curvature.
L’avere introdotto nel ragionamento la topologia sarebbe senza effetti se non ci fosse la possibilità di falsificare o confermare le previsioni che si possono trarre assumendo diversi modelli per lo spazio fisico. Il libro dedica agli effetti osservabili dovuti alle topologie multiconnesse i capitoli dal 16 al 21 e nella postfazione riporta i programmi di osservazione in corso all’epoca della stesura del testo e il dibattito sui primi risultati. Queste osservazioni si basano sul fatto che in un universo multiconnesso una stessa sorgente ci apparirebbe in una molteplicità di immagini in diverse direzioni, sempre che lo spazio fisico fosse più piccolo dello spazio osservabile almeno nella direzione della sorgente (altra affermazione che prima della lettura di questo libro mi avrebbe fatto pensare a un errore di battitura) e che la sorgente fosse più vecchia del tempo necessario per percorrere i diversi cammini. Una sorgente di particolare interesse per questo scopo è la radiazione di fondo, in particolare le sue fluttuazioni (cap.21, 38 e postfazione).
In conclusione della postfazione l’autore afferma che la questione della forma dello spazio al momento della stesura dal testo (2004) era ancora aperta: c’erano stati gruppi di ricerca che dall’analisi delle fluttuazioni della radiazione di fondo escludevano la presenza di segni di uno spazio fisico multiconnesso, altri che dichiaravano di avere identificato alcuni di questi segni.
Grazie mille Fabrizio! (E duemila grazie ad Albertone che, con la sua domanda, ci ha "obbligato" ad approfondire l'argomento).
Ora non resta che utilizzare al meglio le preziose informazioni che hai fornito
Mi sa che questo libro di Luminet lo cerco e cerco anche di capirlo. Grazie Fabrizio e complimenti anche per le tue doti di promotore di libri
Intanto ho inserito una nota in calce a questo articolo (e a quello pubblicato nel 2018), poi vedrò di trovare il modo di utilizzare la sintesi del libro... ma per questo bisognerà coinvolgere il prof.!