Categorie: Buchi neri Fisica
Tags: Alberto Salvagno calcoli matematici elementari
Scritto da: PapalScherzone
Commenti:10
Armiamoci (di buona volontà e calcolatrice) e... partite! **
Ci teneva tanto il nostro Albertone ad andare in vacanza nel buco nero, che lo abbiamo accontentato!
Eccolo immortalato mentre ci sta salutando: in realtà lui è già dentro il buco nero, ma la sua immagine per noi osservatori esterni impiegherà un tempo infinito per scomparire dall'orizzonte degli eventi! Che bello... sarà come continuare averlo tra noi. Ci piacerebbe chiedergli come sta e cosa c'è là dentro, ma niente da fare... nessuna informazione può uscire da lì.
Prima di entrare, però, Albertone ha fatto in tempo a lanciare un messaggio con la sua radio di bordo a modulazione di frequenza quantistica, che ci ha raggiunti istantaneamente: si tratta di alcuni calcoletti che ha effettuato per ingannare il tempo durante il viaggio, giusto per verificare - non per sfiducia, ma per mettersi alla prova (almeno questa è la versione ufficiale) - che i valori riportati QUI siano corretti. Perché - ahinoi! - contro ogni aspettativa, alcuni valori sono risultati diversi. E, a domanda diretta, il nostro professore preferito (che in quel momento con la mano destra stava chiudendo una valigia, con la sinistra si stava difendendo dagli attacchi di coccolite acuta perpretati da quella miciona che risponde al nome di Tigotta e con un piede stava già fuori dalla porta) ha confessato: "ti dirò Albertone... nemmeno io li ho calcolati, ma li ho presi per buoni da una fonte americana degna di fiducia... però, sai... fidarsi è bene e non fidarsi è meglio... Ben vengano altri scrupolosi controllori!!!"
Orsù, quindi, scrupolosi controllori... fatevi avanti! Controllate i calcoli di Albertone e vediamo se ha ragione lui o la fonte americana degna di fiducia!
Questa volta il premio in palio per i volenterosi partecipanti, non sarà il solito "bel niente", ma - udite udite! - tra di essi verrà sorteggiato colui/lei che vincerà un viaggetto nel buco nero per incontrare Albertone e dirgli se i suoi calcoli sono giusti oppure no!
Armatevi quindi, o ardimentosi, di buona volontà e calcolatrice e... partite!
DI SEGUITO I CALCOLI DA VERIFICARE
(potete scrivere i vostri calcoli nei commenti oppure inviarli a papalscherzone@gmail.com)
Prima di tutto ho verificato il raggio di Schwarzschild del buco nero Cygnus X-1 e già che c'ero anche la sua densità:
confermati quindi i tuoi 60 Km di diametro. Ma qui già mi accorgo di qualcosa che non ho capito, perché tu dici: "La zona interna all’orizzonte degli eventi (quella da cui nessuna luce può pervenirci) è di soli 185 km".
Comunque ho poi fatto anche il calcolo dell'attrazione gravitazionale del buco nero a 150 milioni di Km di distanza, la stessa da cui parti che, guarda caso, è anche la distanza Terra-Sole. Ebbene, poiché il buco nero ha una massa 10 volte superiore a quella del sole, anche l'attrazione risulta decuplicata. Me l'aspettavo!
Quindi ho ricalcolato i g per ognuna delle tappe di questo viaggio strabiliante. Ho però trovato delle differenze:
a 1,5 milioni di Km tu parli di 100 g, ma io ho trovato 60;
a 3 mila Km anch'io ho trovato 15 milioni di g;
anche a 600 Km più o meno ci siamo, 400 milioni tu e 375 milioni io;
uguali a 150 Km i 6 miliardi;
a 90 Km invece io calcolo 16 miliardi di g e tu circa il doppio, 30 miliardi;
a 13 Km tu parli di 650 miliardi di g mentre io trovo 800 miliardi;
infine a 4 Km dici che "l'accelerazione ha raggiunto i 2 trilioni di g" mentre io ne calcolo 8,5, sempre che tu mi confermi che stiamo parlando di trilioni all'americana, insomma 1012 e non 1018.
Poi mi è venuto un dubbio: quando si calcola la distanza dal buco nero si deve calcolarla dal suo centro (dove c'è la singolarità) o dal suo orizzonte degli eventi? Cioè quando dici che siamo a 4 Km, devo fare il calcolo su 34 Km (30, raggio del buco nero + 4 Km)? Perché allora il calcolo per me sarebbe questo:
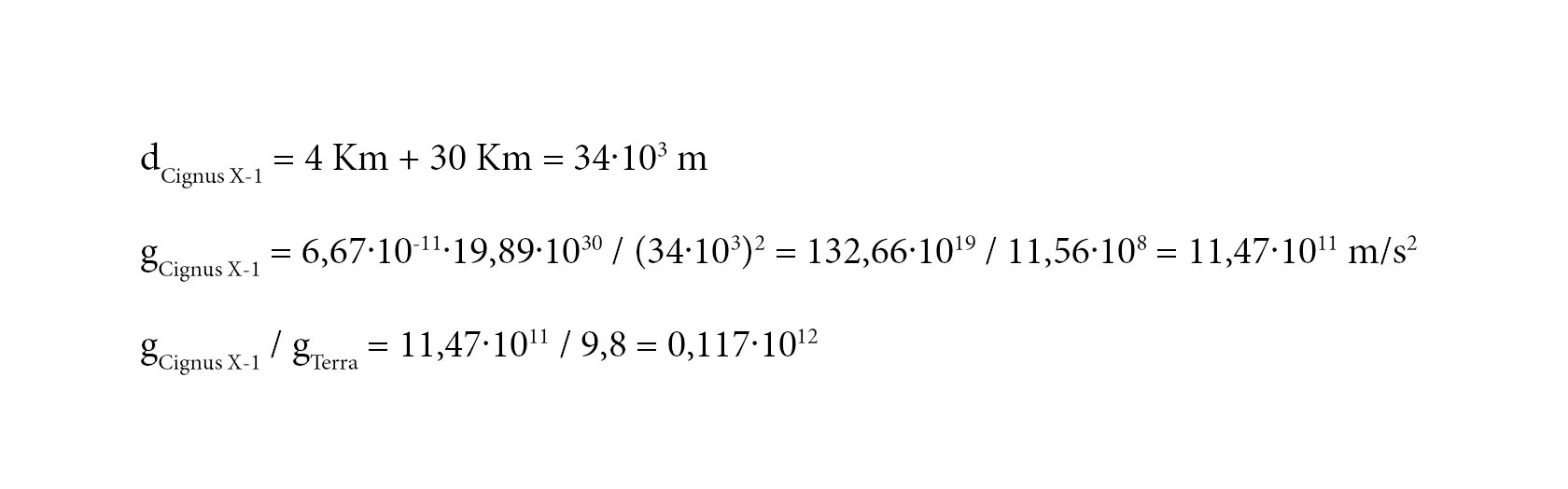
10 commenti
No, non ci credo! Mi sento sempre più coccolato, viziato, ma anche responsabilizzato. Rischio di fare una figuraccia!
E, visto il premio, non mi posso nascondere nemmeno nel buco nero. Speriamo che ci sia almeno un'uscita (attraverso qualche warmhole?) per trasferirmi in un altro Universo dove non mi conoscono :-)
Io rinuncio , mi fido di chi ne sa più di me !!!
Scherzare con te, Albertone, è solo un piacere! E se lo si può fare, come in questo caso, anche “a fin di bene”, il piacere è doppio.
Rimpiango solo di non aver potuto vedere la tua espressione quando hai aperto il blog (o Facebook?) e ti sei visto in primo piano sul buco nero!!
Cara Giuliana, sono completamente d’accordo con te! Non a caso nel titolo ho scritto "partite" non "partiamo"
Il calcolo del raggio dell'orizzonte degli eventi fatto da Alberto credo sia corretto nel caso di un buco nero statico e di massa 10 volte la massa solare.
Le stime più recenti portano la massa di Cygnus X-1 a circa 20 masse solari. Inoltre sembra che abbia una velocità di rotazione notevole.
Il risultato numerico che si ottiene non dovrebbe essere lontano da quello di Alberto poiché le correzioni da fare rispetto al caso statico tendono a compensarsi. Il raddoppio della massa fa raddoppiare il raggio dell'orizzonte degli eventi. La rotazione invece riduce il raggio fino a dimezzarlo per rotazioni estreme. Quindi il risultato non dovrebbe essere molto lontano dai 30km se la rotazione è quella che ho visto ipotizzare. Qui parliamo di raggio, ma occorre chiarire che il suo significato non è detto che corrisponda al significato geometrico che normalmente gli diamo.
Allora il 185 come esce fuori? Non lo so per certo perchè non ho visto l'articolo che ha utilizzato Enzo. Però questo numero appare in alcuni articoli.
Si tratta della stima, basata sulle osservazioni, del massimo diametro di questo oggetto espressa in miglia. La stima è fatta sulla base della osservazione della durata degli impulsi di raggi X emessi da questa sorgente. Gli impulsi durano 1ms, da questo deducono che la sorgente deve avere un diametro inferiore alla distanza che la luce copre in 1ms, cioè 300km. Espressi in miglia sono circa 187 mi, che arrotondate vengono riportate come 185 mi.
Da notare che la stima del raggio dell'orizzonte degli eventi è un esercizio che si basa sulla teoria e sull'ipotesi che si tratti di un buco nero. Per Cygnus X-1 non ha una corrispondente osservativa.
Grazie Fabrizio, sapevo di poter contare su di te!
Caro Fabrizio, se non avessi saputo che Enzo era già con la valigia in mano, la questione che volevo porgli era proprio da dove saltava fuori la frase La zona interna all’orizzonte degli eventi (quella da cui nessuna luce può pervenirci) è di soli 185 km, visto che poco prima nello stesso articolo aveva parlato di un oggetto che ha una massa pari a 10 volte quella del Sole, concentrata in un volume di soltanto 60 km di diametro.
Trovo da qualche parte in questo sito la spiegazione di perché se il buco è in rotazione appare più striminzito? Mi sarei aspettato il contrario, pensando in modo classico alla forza centrifuga
Tutto quello che è stato scritto sui buchi neri rotanti, Alberto, lo trovi qui http://www.infinitoteatrodelcosmo.it/2018/04/05/buchi-neri-rotanti/. Non mi sembra che contenga la risposta alla tua domanda sul raggio che diminuisce, ma potrei sbagliarmi...
Pensandoci su la faccenda deve avere a che fare con il pattinatore che stringe le braccia per girare più forte...
Ho provato ad approfondire la questione della forma dell'orizzonte degli eventi di un buco nero rotante anche sulla base delle considerazioni di Alberto. Sono riuscito appena a scalfire l'argomento che mi è parso molto complesso. Comunque qualcosa credo di avere ottenuto. Provo a riportarlo perché credo metta in evidenza alcune 'trappole' che si possono incontrare trattando lo spazio deformato della Relatività Generale.
Parto da quanto Enzo ha illustrato in questo articolo, riassumendo di seguito le informazioni riguardanti l'orizzonte degli eventi.
La superficie dell'orizzonte degli eventi di un buco nero rotante è caratterizzata da un valore costante della coordinata denominata r. Questo valore dipende dalla massa (M) del buco nero e dalla sua velocità di rotazione. Il valore costante della coordinata r è normalmente indicato con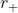
, mi riferisco all'orizzonte degli eventi esterno. Il suo valore è 
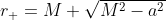. Il parametro a caratterizza la velocità di rotazione del buco nero. Il valore a=0 rappresenta un buco nero statico come quello studiato da Schwarzschild. Il valore a=M credo sia il massimo. Le unità di misura di queste formule sono quelle spesso utilizzate in relatività generale dove distanze, tempi e masse sono espresse con la stessa unità di misura, normalmente in metri.
Quindi la superficie dell'orizzonte degli eventi è definita da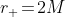
per un buco nero statico e da 
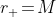per un buco nero che ruota alla velocità massima.
Bene, detto così potrebbe sembrare che la superficie dell'orizzonte degli eventi sia sferica con raggio più piccolo per i buchi neri che ruotano più velocemente.
Ma questa è una 'illusione' dovuta al tipo di coordinate utilizzate. La coordinata r, che fa parte delle coordinate denominate di Boyer-Lindquist, è alquanto strana.
Per aiutare a capire le caratteristiche geometriche della superficie definita dalla coordinata r costante,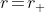
, i fisici cercano una sua rappresentazione nello spazio che ci è più familiare: lo spazio euclideo tridimensionale. Una rappresentazione che riporti correttamente le distanze sulla superficie con la nostra usuale metrica, per questo è chiamata isometrica.
Questa rappresentazione fu trovata ed analizzata da Larry Smarr nel 1973. Nella figura ci sono le tracce di queste superfici su un piano che passa per l'asse di rotazione. Per queste superfici intendo le superfici con la coordinata r di Boyer-Lindquist costante pari a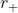
. Evidentemente queste superfici non hanno un raggio Euclideo costante.
Le superfici che cerchiamo si ottengono ruotando queste curve intorno all'asse. Sono quindi delle superfici sferoidali schiacciate ai poli. Tanto più schiacciate quanto più alta è la velocità di rotazione. In quest'altra figura c'è un tentativo di rappresentazione 3D di uno di questi sferoidi. Per dare un'idea della forma ho aggiunto la linea circolare dell'equatore, uno dei meridiani e l'asse di rotazione.
Ovviamente non c'è nulla di materiale in queste superfici o linee.
Queste forme sembrano avvalorare l'impressione di Alberto che c'entri qualcosa la forza centrifuga. Non ho elementi diretti per confermare questa impressione. Le figure sono ricavabili dalla elaborazione delle componenti delle metriche senza l'intervento della forza centrifuga. Però, il premio Nobel Kip Thorne, uno dei maggiori esperti di relatività generale, in un suo libro divulgativo chiama in causa proprio la forza centrifuga per spiegare la forma di queste superfici.
Si può dire che la forma 'reale' della superfici dell'orizzonte degli eventi è quella in figura?
Non lo so. Non so neanche se si può dare un senso a questa domanda. Il dubbio più forte viene dal fatto che queste superfici isometriche nello spazio Euclideo tridimensionale esistono solo per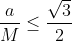
. Per velocità di rotazione più elevata non è possibile costruirle, ma comunque buchi neri con queste velocità di rotazione sembrano possibili.
Un altro punto 'strano' su cui fare attenzione è il fatto che sono le superfici che sono isometriche e non ciò che è all'interno o all'esterno della superficie. Questo significa, ad esempio, che è corretto calcolare la lunghezza della linea dell'equatore o di un meridiano con questa rappresentazione. Non è invece assolutamente corretto pensare che la distanza dell'equatore dal centro o la distanza di uno dei poli dal centro sia quella rappresentata in figura.
Una triste nota finale
Robert Hamilton Boyer, il co-ideatore delle coordinate utilizzate per descrivere i Buchi Neri rotanti, fu ucciso nel 1966 all'età di 34 anni, insieme ad altre 14 persone, in una delle troppe frequenti stragi che avvengono negli USA.
Aggiungo un paio di cose che mi sono sfuggite nello scrivere il commento sopra.