Categorie: Relatività
Tags: Minkowski relatività della simultaneità RR
Scritto da: Vincenzo Zappalà
Commenti:38
Relatività Ristretta Rivista. 3: Simultaneità relativa **
Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento
Parliamo di simultaneità di due eventi quando essi si verificano nello stesso momento. Ne consegue che se, ad esempio, si accendono simultaneamente due lampadine poste alla stessa distanza da noi, la loro luce deve raggiungerci nel medesimo istante. Invertendo il concetto, possiamo dire che se la luce di due lampadine poste alla stessa distanza ci raggiunge nello stesso istante, i due eventi luminosi devono essere stati simultanei. Questo accade nella vita di tutti i giorni, ma in realtà la simultaneità è un fenomeno che dipende molto dal sistema di riferimento. Vedremo come nella RR acquisti un’importanza fondamentale.
Liberiamoci subito dalla confusione che può derivare da un’apparente simultaneità di due eventi, posti a distanze diverse. In un medesimo istante potremmo vedere accendersi la luce di una supernova e quella del lampione posto all’angolo della strada di casa. Non potremmo, però, certo dire che i due eventi sono simultanei! La luce della supernova ha dovuto viaggiare per milioni di anni luce, mentre quella del lampione solo una frazione di secondo. Questa apparente simultaneità è ovviamente dovuta alla velocità “finita” della luce, che, benché rapidissima, impiega un certo tempo per percorrere un certo spazio.
Per parlare di simultaneità e di relatività della simultaneità dobbiamo, quindi, metterci nelle giuste condizioni, ossia in una posizione tale che la luce debba percorrere una distanza esattamente uguale rispetto a noi che la riceviamo. Nella vita quotidiana, gli eventi che soddisfano questa condizione sono giudicati simultanei qualsiasi sia il sistema di riferimento da cui sono osservati. In altre parole, vale la relatività di Galileo che ci dice che il tempo scorre nello stesso modo in qualsiasi sistema di riferimento si osservi. Ossia, vale t = t’. Ripetiamo ancora: se due eventi sono simultanei in un certo sistema di riferimento, noi accettiamo immediatamente che essi siano simultanei anche per un diverso sistema di riferimento. Questa abitudine, confortata dalla realtà delle cose che ci circondano, crea non poca difficoltà nel pensare che la simultaneità possa dipendere dal sistema da cui si osservano i due eventi. Nella RR, invece, il concetto di relatività della simultaneità è un dato di fatto. Anzi, è forse il più importante concetto, dato che tutto deriva proprio da lui, come la dilatazione dei tempi e la contrazione delle lunghezze.
Se non si comprende perfettamente la simultaneità, e come essa possa dipendere dal sistema di riferimento, la strada verso la relatività ristretta è una salita verso una cima inviolabile. Cerchiamo allora di spiegarla nel modo più semplice possibile e di applicarla al caso del diagramma di Minkowski. Ci accorgeremo che proprio quest’ultimo riesce a sintetizzarla e a dimostrarla in modo veramente immediato.
Ricordiamo, innanzitutto, come abbiamo fatto per sincronizzare gli orologi di un sistema di riferimento. Ci siamo portati nel punto di mezzo di una certa asta di lunghezza misurata perfettamente e abbiamo acceso una lampadina. Nel momento in cui la luce giunge ai due estremi vengono fatti partire gli orologi. La distanza tra la lampadina C e i due orologi A e B è identica per costruzione e quindi l’arrivo della luce deve essere contemporanea. I due orologi segnano lo stesso tempo.
Invertendo il procedimento, otteniamo un classico esempio di simultaneità di due eventi.
Mettiamo due lampadine in A e B e le accendiamo a un certo istante. La luce arriva in C simultaneamente, dato che è partita nello stesso momento (per definizione di sincronizzazione) e percorre la stessa distanza. C dice che i due eventi (accensione delle lampadine di A e di B) sono avvenuti simultaneamente. Riassumendo, l’operazione di sincronizzazione permette di ottenere la simultaneità.
Possiamo, perciò, concludere che se la luce partita da A e da B non giunge in C nello stesso momento vuole dire che gli orologi di A e di B NON sono sincronizzati. Questo fatto è importantissimo! Un’apparente mancanza di simultaneità assicura che i due orologi del sistema di riferimento non possono essere sincronizzati, ossia non possono segnare la stessa ora. Il processo di sincronizzazione e di simultaneità vengono rappresentati schematicamente nella Fig. 1. Sopra si accende la lampadina e si sincronizzano gli orologi; sotto si accendono le lampadine quando gli orologi segnano la stessa ora e la luce arriva al centro simultaneamente.
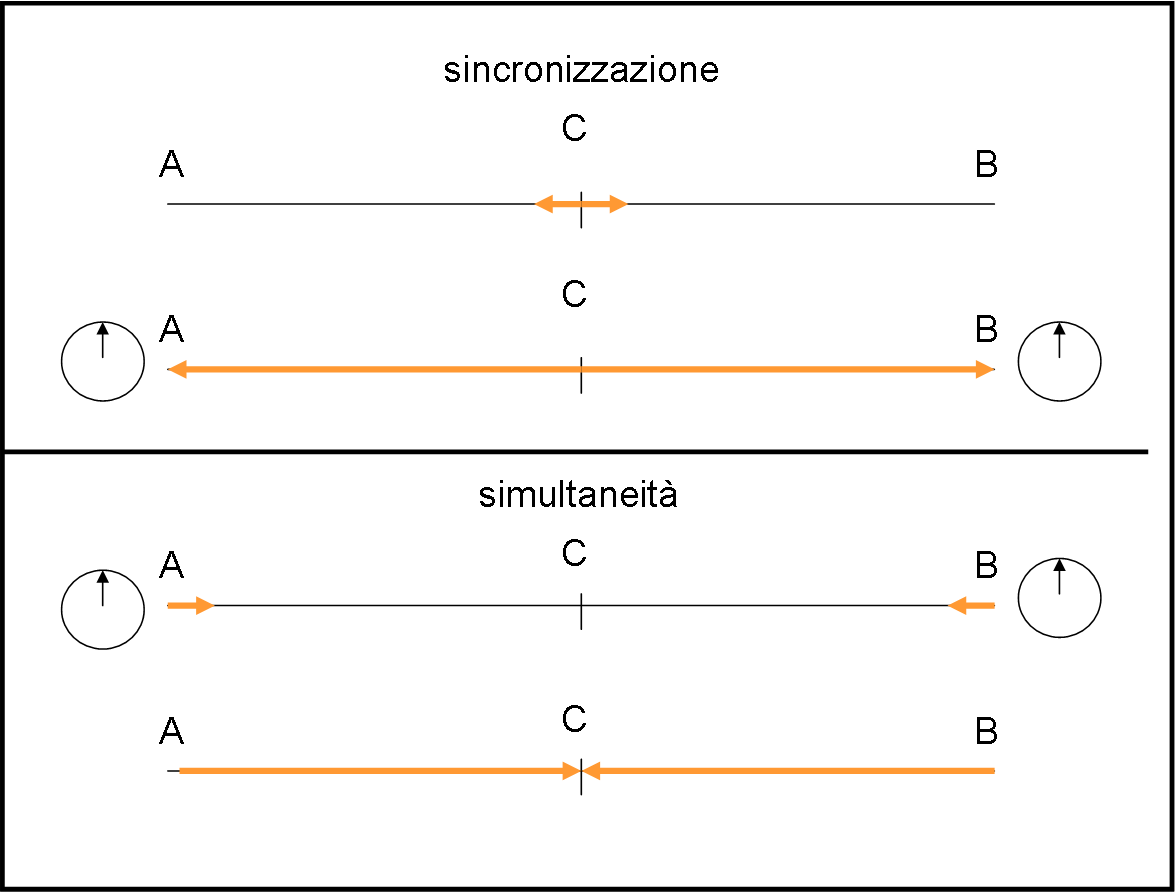
Queste operazioni sono svolte e confermate in tutti i sistemi di riferimento. Siamo quindi sicuri che per ognuno di loro vale la simultaneità di due eventi, ogni volta che le condizioni sono quelle giuste (stessa distanza dell’osservatore e orologi sincronizzati). Tuttavia, rimane il problema dell’osservazione da un sistema di riferimento diverso: siamo sicuri che ogni sistema è stato sincronizzato, ma NON siamo sicuri che chi osserva da un altro sistema confermi quanto è stato eseguito. In parole povere, due eventi che sono simultanei in un sistema di riferimento, possono anche apparire non simultanei se osservati da un altro. Se questo avviene, chi osserva non può che concludere che i due orologi NON sono stati sincronizzati perfettamente.
Nel mondo di Galileo questo rischio non si corre mai, dato che il tempo impiegato dalla luce per raggiungere l’osservatore può essere considerato nullo. Questo dato di fatto non deve, però, trarci in inganno sul concetto di simultaneità. La conclusione “sembra” normale solo perché la luce “sembra” avere una velocità infinita.
Consideriamo un classico esempio, quello di un treno (o un autobus o un’astronave) che riesca a viaggiare a una velocità comparabile con quella della luce. La faccenda si complica, ma rimane estremamente logica. Cerchiamo di proseguire con molta calma e attenzione.
Il sistema treno ha gli orologi perfettamente sincronizzati e quindi non si preoccupa assolutamente della sua velocità. Noi ci muoviamo solidalmente con lui e quindi la luce di due lampadine poste ai suoi bordi estremi, accese alla stessa ora, arriva sempre nello stesso momento al centro del treno, dove siamo noi. I due eventi sono sempre simultanei e di conseguenza abbiamo un’ulteriore conferma che i due orologi posti in A e B sono perfettamente sincronizzati. Ricordiamoci, infatti, che un fenomeno fisico è indipendente dal sistema di riferimento inerziale in cui si svolge. Ciò vuol dire che sia se si sta fermi sia che si viaggi ad altissima velocità la luce delle due lampadine deve arrivare nel punto centrale simultaneamente. Questo concetto deve essere digerito perfettamente, altrimenti si perde subito il filo. Tuttavia, non dice niente di strano, dato che capita anche per Galileo: se versate l’acqua in un bicchiere, il fenomeno è identico sia se siete fermi sia se state viaggiando su un treno (a parte eventuali scossoni che renderebbero NON INERZIALE il sistema).
Vediamo al rallentatore, in Fig. 2, ciò che succede, anche se ormai lo conosciamo molto bene. Possiamo permetterci di indicare il tempo che scorre lungo un’asse verticale, mentre il treno è situato nello spazio orizzontale. Siamo all’interno del sistema treno e indichiamo tutto con l’apice. All’istante t’ = t’0 , la luce parte da A’ e da B’. All’istante t1 è già giunta a metà della sua strada. Al tempo t2 ci colpisce in C’. In altre parole, la luce partita da A’ e quella partita da B’ si incontrano nel punto C’, centro del treno, nello stesso identico istante. Abbiamo disegnato un bel triangolo isoscele. Il treno è stato disegnato in rosso (freccia rossa?) e percorre nel tempo lo spazio-tempo rosso dal basso verso l’alto. Nel suo sistema non si muove nello spazio e quindi si muove solo lungo l’asse del tempo, come ormai abbiamo spiegato molto bene la volta scorsa. Questo è quello che capita sempre, osservando dall’interno di un sistema che si considera fermo.
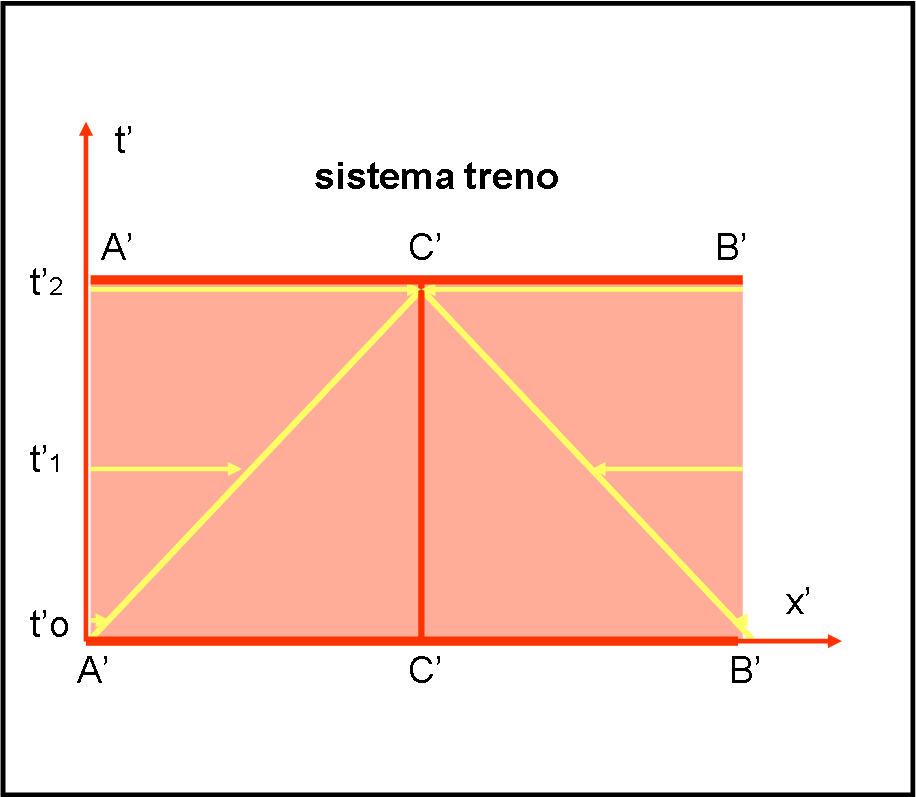
Possiamo cambiare la velocità del treno quanto vogliamo, ma il risultato è sempre lo stesso: la sincronizzazione non perdona e la luce viaggia sempre alla stessa velocità (fatto estremamente importante e fondamentale). Il nostro sistema per noi rimane sempre fermo, dato che non possiamo accorgerci se ci muoviamo oppure no, come dice la relatività galileiana e anche quella einsteniana. Quel simpatico triangolo isoscele vale quindi per qualsiasi sistema di riferimento “treno”. Ovviamente vale anche se il treno è realmente fermo in una stazione.
Scendiamo dal treno e mettiamoci a metà strada (C) tra le due lampadine (A e B), ma sul marciapiede. Abbiamo tolto gli apici, dato che siamo in un sistema di riferimento che d’ora in poi è quello che considereremo fermo e rispetto a cui disegneremo ciò che succede. A corrisponde spazialmente ad A’, B a B’ e C a C’, ma A, B e C sono sul marciapiede, mentre A’, B’ e C’ sono sul treno. Il treno è fermo, ma eseguiamo ugualmente l’esperimento di prima. Facciamo accendere le lampadine che stanno sul treno, secondo gli orologi del treno, e vediamo cosa succede. Notiamo che la luce parte in realtà da A’ e B’, ma per chi sta sul marciapiede è come se partisse da A e da B.
Perfetto: la luce arriva contemporaneamente in C’, che coincide con C, anche guardando dalla nostra posizione “esterna” al treno. La simultaneità si è mantenuta. Gli orologi della panchina sono perfettamente in accordo tra loro e con quelli del treno. Non vi è bisogno di fare una figura, dato che la situazione è perfettamente identica a quella di Fig. 2.
Anche l’osservatore posto sul marciapiede, nel punto giusto, non può che confermare il triangolo isoscele di prima, anche se le lampadine appartengono al treno. D’altra parte, se portasse le due lampadine sul marciapiede in corrispondenza degli estremi del treno e le facesse accendere secondo gli orologi della banchina confermerebbe la simultaneità.
Insomma, niente cambia sia cambiando sistema, sia guardando ciò che capita in un altro. Fatemi essere infantile e ripetere a parole quattro casi che appaiono perfettamente identici tra loro: (1) siamo al centro del treno con le lampadine sul treno; (2) siamo al centro del marciapiede con le due lampadine poste sul marciapiede; (3) le lampadine sono poste sul treno e noi siamo al centro del marciapiede; (4) siamo al cento del treno, ma le due lampadine sono poste sul marciapiede. Tutte le figure sono perfettamente identiche: la luce giunge al centro simultaneamente in tutti i casi. Beh… ci voleva poco, dato che il treno è fermo! Galileo, comunque, aveva proprio ragione, almeno in questo caso: la simultaneità si mantiene in tutti i sistemi di riferimento.
Tuttavia, anche se si muovesse a velocità “normale”, la faccenda apparirebbe perfettamente analoga: la luce è talmente veloce che riesce ad arrivare al centro di ogni sistema sempre simultaneamente. In altre parole, la figura precedente non cambierebbe assolutamente anche utilizzando sofisticatissimi strumenti di misura. Galileo continua ad avere ragione…
Non ci resta adesso che mettere in rapido movimento il treno, ripetendo quanto fatto precedentemente. Ci basta confrontare due casi: quello in cui l’osservatore è al centro del treno e quello in cui l’osservatore è al centro del marciapiede, ma con le lampadine messe sul treno (è facilissimo comprendere che mettendo le lampadine a terra ciò che succede sarebbe perfettamente ribaltabile, dato che per chi viaggia sul treno si muove il marciapiede). Ciò che cambia, adesso, è che la velocità del treno è comparabile con quella della luce, ossia ne rappresenta una frazione non trascurabile.
Per svolgere al meglio l’esperimento ci facciamo aiutare da un amico. Noi ci mettiamo al centro del treno, in C’ (in movimento con velocità v) e il nostro amico al centro del marciapiede, che corrisponde al centro del treno (a treno fermo). La situazione è quella di Fig. 3 che sembra perfettamente identica a quanto fatto finora.
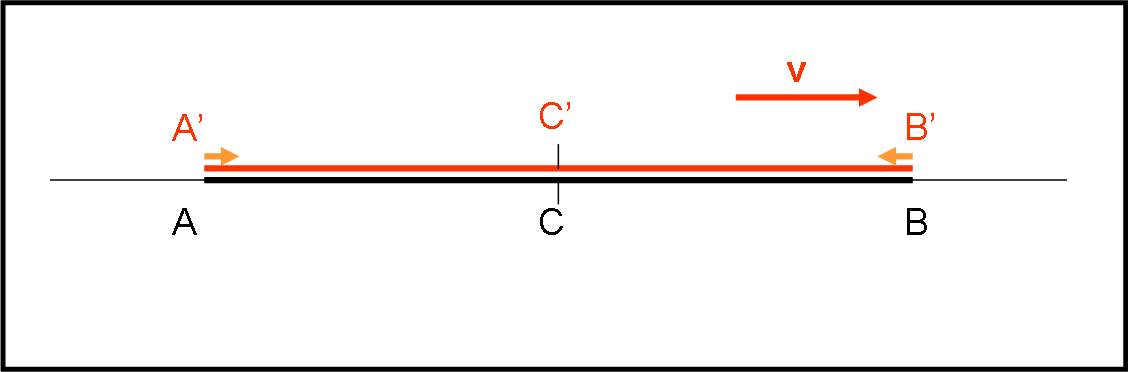
Il momento fondamentale di partenza dell’esperimento è scelto con molta cura. I due estremi del treno A’ e B’ devono coincidere con i punti del marciapiede A e B; come conseguenza anche il punto C’ coincide con C. Le lampadine sono sul treno in A’ e B’. Esse vengono accese in quell’ istante. La luce inizia a viaggiare infischiandosene del tutto del sistema in cui si trova (questo ce lo dice Einstein!). Essa arriva contemporaneamente nel punto C’, come succedeva a treno fermo. Questo lo abbiamo già detto e ridetto molte volte e il fenomeno che avviene è sempre lo stesso: la luce parte da A’ e B’ e arriva in C’ simultaneamente. Si ripete il triangolo isoscele.
La faccenda si complica per il nostro amico posto in C. Lui crede ciecamente a quanto gli è stato detto: le due lampadine si accendono sul treno nello stesso momento, proprio quando coincidono spazialmente con A e B. Lui sa perfettamente che, sul treno, la luce deve raggiungere contemporaneamente noi che siamo in C’, ma sa anche che la luce inviata nello stesso istante da due posizioni che coincidono con A e B dovrebbe arrivare simultaneamente anche in C dove si trova lui.
Purtroppo, si sbaglia di grosso: le due cose non possono avvenire entrambe! Il punto C’, così come A’ e B’, si spostano verso destra con velocità elevata e la luce arriva in C’ quando ormai esso si è spostato, nel sistema del marciapiede, rispetto alla posizione iniziale in cui coincideva con C. Per noi che stiamo in C’ tutto è andato benissimo: la luce è, infatti, arrivata simultanea nel punto di mezzo, indipendentemente dalla velocità del treno.
L’amico in C è, invece, disorientato: la luce che è partita da A (quando coincideva con A’) e quella che è partita da B (quando coincideva con B’) dovrebbero arrivare simultaneamente fino a lui che è in C (che coincideva con C’). E, invece, ecco che la luce di A transita tranquillamente davanti a C senza che quella proveniente da B sia ancora in vista. Dato che la luce di A lo raggiunge per prima, vuol dire che è stata accesa prima di quella di B. Gli eventi non sono, perciò, simultanei.
Non vi è niente da fare, la conclusione di C può essere una e una sola: due eventi che sono simultanei in un dato sistema di riferimento inerziale (il treno) non lo sono in un altro sistema (il marciapiede), dunque la simultaneità di due eventi che avvengono in punti distinti dello spazio non rappresenta un fatto assoluto ma è relativo al sistema di riferimento.
Ma, se nel treno le lampadine si sono accese nello stesso istante, vuol dire che si sono accese quando i due orologi posti agli estremi A’e B’della carrozza segnavano lo stesso tempo (t’A’ = t’B’). Allora, se nel riferimento a terra gli eventi appaiono non simultanei, questo vuol dire che gli orologi posti a terra nei punti Ae B segnavano tempi tA e tB diversi fra loro e, quindi, almeno uno dei due tempi deve differire dai tempi misurati dagli orologi in A’e B’. Il tempo segnato dagli orologi non è, perciò, un tempo assoluto ma è relativo al sistema di riferimento.
Vediamo ciò che succede nella Fig. 4, molto semplificata, ma più che sufficiente a farci capire, qualitativamente, la simultaneità relativa.
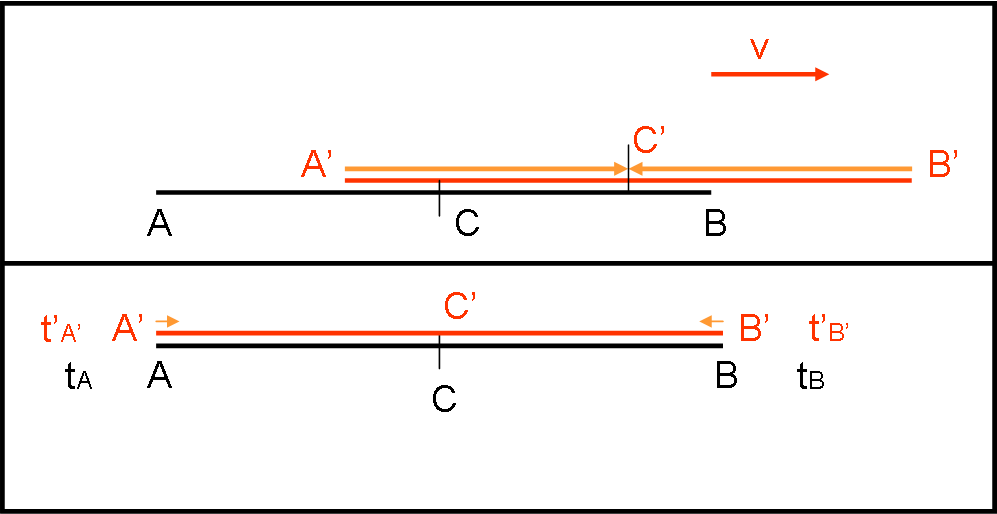
In basso, la luce parte da A’ e B’ simultaneamente per l’osservatore in C’. L’osservatore in C pensa che i due eventi siano simultanei anche per lui e si attende che la luce di A e B (coincidenti con A’ e B’ all’accensione delle lampadine) arrivino contemporaneamente in C. In alto, però, C si accorge che quando la luce di A’ e quella di B’ arrivano in C’, la luce di A’ è già passata dalla sua posizione centrale sul marciapiede, ma non certo quella di B’ che ha appena raggiunto C’. La luce deve essere partita prima da A che non da B. I tempi tA e tB devono essere diversi, per potere avere la simultaneità sul treno. In altre parole, t’A’ e t’B’ sono identici per forza, ma non lo possono essere tA’ e tB’ che coincidono con tA e tB per l’amico sul marciapiede.
La Fig. 4 ci dimostra senza alcun dubbio la relatività della simultaneità, ma sarebbe molto meglio disegnare qualcosa di più preciso. Fermi tutti! Sappiamo come fare, ricordando il triangolo isoscele di Fig. 2.
Costruiamo, allora, la Fig. 5 seguendo lo stesso procedimento, ma tenendo conto del movimento del treno. In nero vi è il sistema del marciapiede, proprio quello rispetto al quale vogliamo disegnare l’intero fenomeno. In rosso vi è il sistema treno A’B’ che si muove verso destra con una certa velocità v. La luce parte dal punto A’, coincidente con A, e viaggia secondo una retta inclinata di 45° (abbiamo scelto una scala che ci sarà molto utile in seguito). Il punto centrale del treno C’ si porta in C’’ quando viene raggiunto dalla luce di A’, mentre il punto A’ si è portato in A”, descrivendo il bordo sinistro del treno.
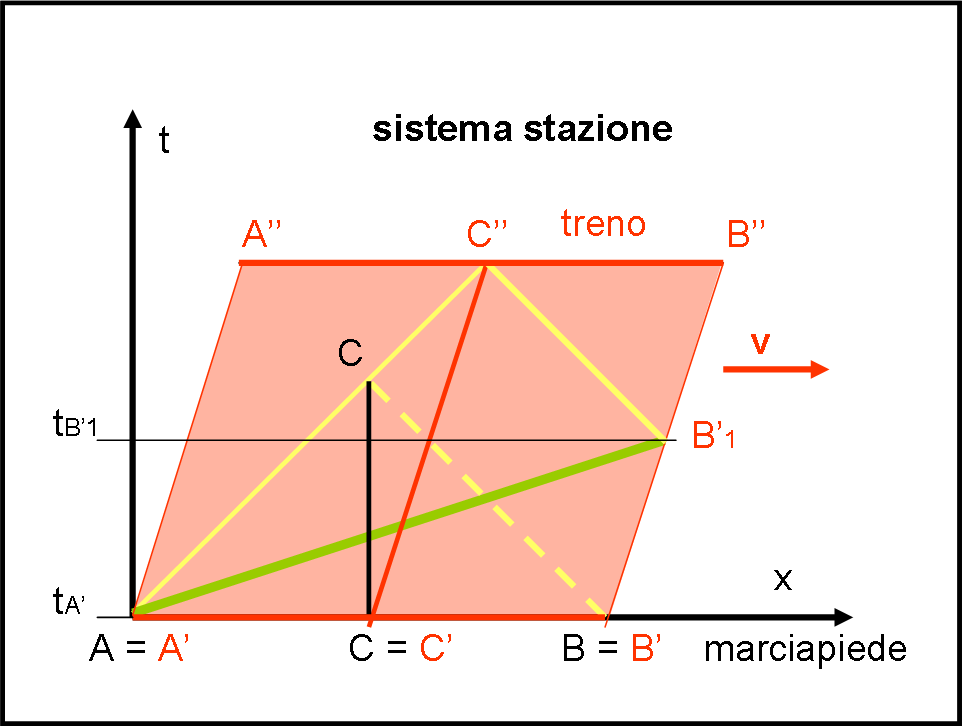
Dato che la luce partita da B’ deve raggiungere C’ nello stesso momento di quella di A’ non è difficile trovare il momento in cui essa è partita da B’, secondo il sistema del marciapiede. Basta infatti tracciare da C” una retta inclinata di 45° (la luce) fino a incontrare la traccia B’B” del bordo destro del treno. Indichiamo l’intersezione con B’1. Nel sistema del marciapiede la luce deve essere partita simultaneamente da A’ e da B’1 per potersi incontrare in C’’ allo stesso istante. Come già detto, questo fatto comporta che secondo il sistema del marciapiede gli eventi di accensione della luce in A’ e B’1 non possono essere simultanei dato che avvengono ai tempi tA’ e tB’1 nettamente diversi tra loro. Questi sono, però, i tempi che permettono agli eventi A’ e B’ di essere simultanei nel sistema treno. Essi devono quindi coincidere nel sistema treno, ossia essi devono soddisfare la relazione t’A’ = t’B’1. La linea A’ B’1 è, quindi, asse di simultaneità per il sistema treno rappresentato nel sistema marciapiede. Abbiamo rappresentato la relatività della simultaneità, ma abbiamo anche determinato una retta che deve essere parallela all’asse x’ del sistema treno. Se ponessimo t’A’ = 0 , avremmo proprio l’asse x’.
In poche parole, abbiamo usato un altro metodo per determinate gli assi del sistema di riferimento in movimento rispetto a quello fermo. Uno è ovviamente la retta A’A’’ che indica lo spostamento del punto A’ del treno rappresentato nel sistema marciapiede. A’, nel sistema treno, sta, infatti, fermo e quindi la retta AA’ indica proprio l’asse t’ (asse di immobilità). L’altro asse è quello di simultaneità, in cui il tempo è uguale a zero, ossia proprio l’asse x’
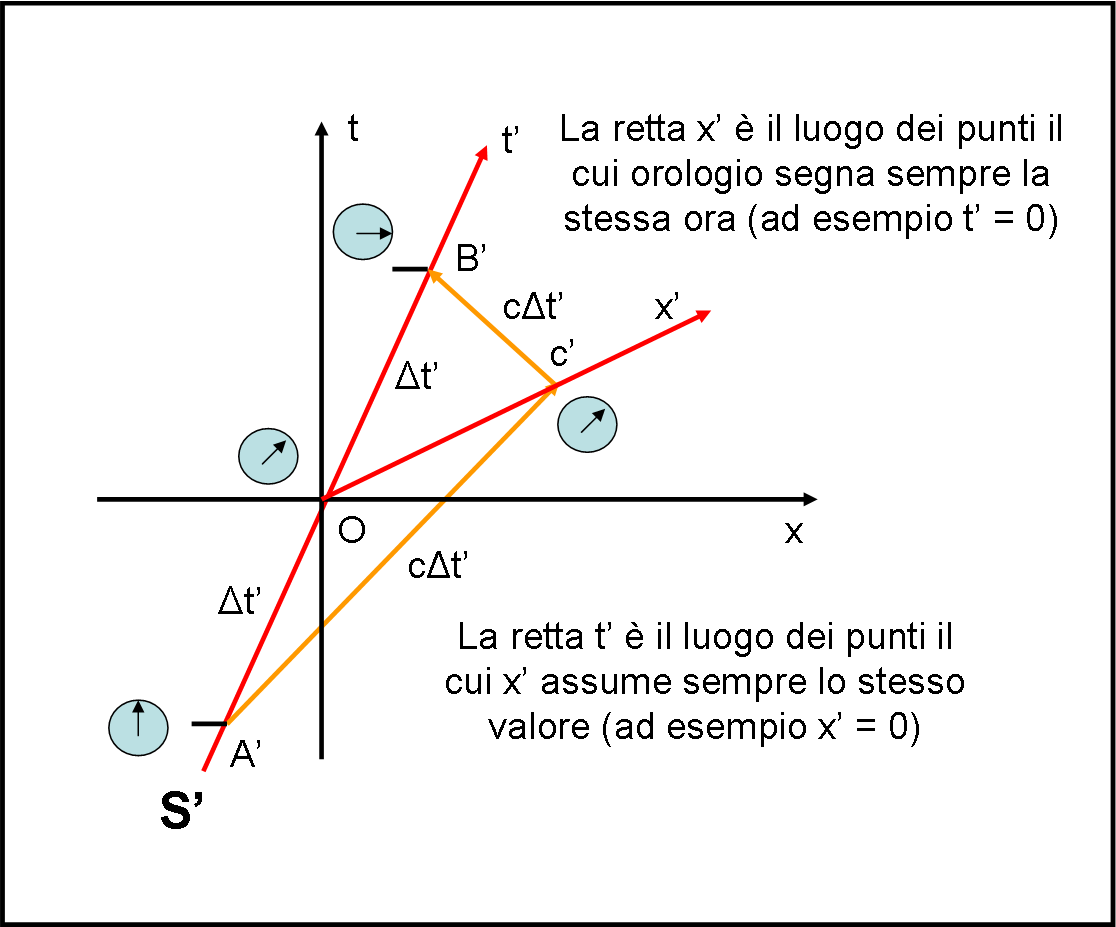
A questo punto possiamo tornare a leggere questo articolo (e il relativo quiz precedente) per renderci conto della perfetta uguaglianza del procedimento utilizzato. In particolare guardiamo la Fig. 45 (che riportiamo anche qui) e confrontiamola con quella appena ottenuta (Fig. 5).
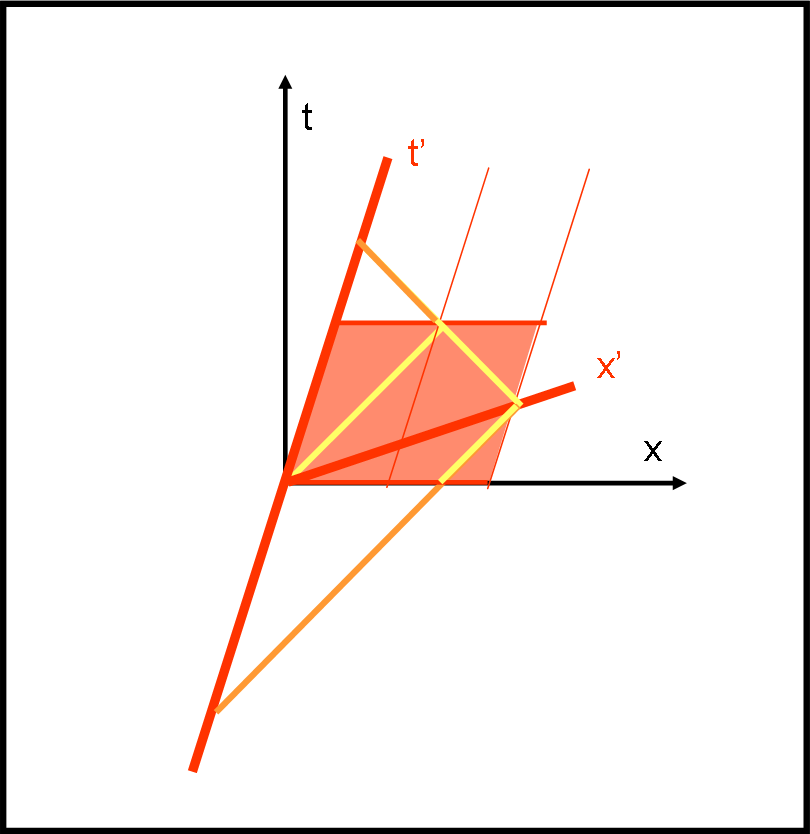
Per maggiore chiarezza riportiamo anche la Fig. 6 che rappresenta l’unione delle due figure. Essa dovrebbe chiarire molti dubbi, se ci si riflette con attenzione.
Quasi senza volerlo, attraverso treni e marciapiedi, siamo arrivati a utilizzare il diagramma di Minkowski. Ci siamo accorti che, in fondo non è altro che un metodo schematico e preciso per ridurre di molto tante spiegazioni verbali…
Notiamo ancora due cose: (1) la relatività della simultaneità porta immediatamente alla relatività del tempo (l’abbiamo dimostrato poco fa); due orologi posti in posizioni diverse segnano, infatti, ore diverse se cambia il sistema di riferimento. (2) La lunghezza di un’asta che si mantiene costante in un sistema in moto, può essere misurata in un sistema fermo solo attraverso due orologi diversi, allo stesso identico istante. Ma, abbiamo appena visto, che due orologi di questo genere segnano ore diverse. Ne segue che se il tempo è relativo al sistema, lo deve essere anche la lunghezza dell’asta.
Ricordate che la vera differenza nasce sempre dall’usare un solo orologio oppure due diversi!
Come si vede molto chiaramente, dilatazione dei tempi e contrazione delle lunghezze derivano naturalmente dalla relatività della simultaneità. D’altra parte, abbiamo visto che essa, da sola, ci ha permesso di tracciare gli assi x’ e t’ del sistema in moto, nel sistema fermo. Il diagramma è quindi perfettamente in grado di spiegare graficamente anche gli effetti più famosi della RR.
Concludiamo, ripetendo ancora una volta che senza capire la simultaneità e la sua relatività, tutta la RR si costruisce come un castello di carte molto traballante, pronto a cadere al primo minimo dubbio.
Seguendo un consiglio di Paolo, propongo un “semplice” test per mettere alla prova chi volesse verificare la propria comprensione dell’intera faccenda.
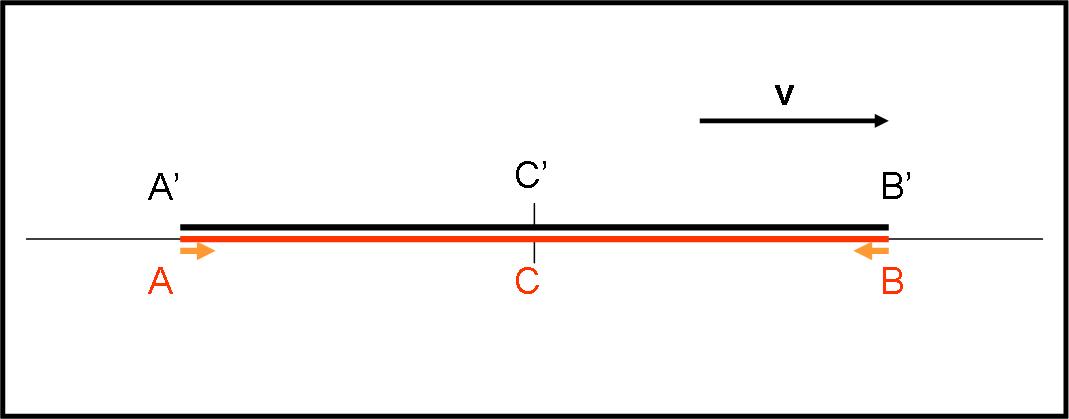
Immaginate di mettere le due lampadine sul marciapiede, in A e B, e di farle accendere simultaneamente in quel sistema. Disegnate il grafico di prima (ossia determinate la simultaneità) ponendo come sistema di riferimento fisso quello del treno. Per lui si accende prima A o prima B? La figura di partenza è la Fig. 7, quasi identica alla Fig. 3, dove sono stati invertiti i colori del treno e del marciapiede, per facilitare l’esecuzione. Ovviamente, il treno si muove sempre verso destra.
La prossima volta faremo il punto su cosa è veramente relativo e su cosa è assoluto. Ci servirà a capire meglio cosa sia un evento e come differisca da un punto. Un articolo molto breve che preferisco, però, tenere separato. Poi torneremo a Minkowski con le idee più chiare (spero).
Spero proprio di essere riuscito a rendere il tutto molto più semplice e intuitivo… mamma mia, che fatica!






38 commenti
Caro Enzo la tua fatica merita quantomeno un grazie , forse non si poteva fare di meglio per fare comprendere fondamentali concetti . Grazie ancora
grazie a te Claudio... ce la sto mettendo tutta...

Fantastico, praticamente un terzo metodo per ricavare l’asse di simultaneità.
Siamo passati da un metodo geometrico, a uno puramente analitico/matematico, a uno, diciamo, puramente pratico.
Non è una cosa da poco.
Vorrei fare delle piccole considerazioni, più che altro per verificare se ho capito bene, perché questo argomento è troppo fondamentale per non essere compreso a fondo.
In riferimento al grafico di figura 5, devo concludere che la luce posta in B’, per il sistema fisso non solo parte dopo e precisamente al tempo tB’1 ma anche da un punto dello spazio spostato, dato che nell’ intervallo di tempo tB’1-tA’ il treno si è nel frattempo spostato.
E’ corretta l’analisi?
Questa mancanza di simultaneità per il sistema fisso associata allo spostamento porta come conseguenza una percezione diversa delle lunghezze come ad esempio la distanza tra A’ e B’, giusto?
Adesso proviamo a fare un esempio terra terra, che per me rappresenta il nocciolo di tutto.
Se insieme alle lampadine poste in A’ e B’ ci mettiamo due persone gemelle identiche di aspetto e di età, chi si trova in C e in C’ cosa vedono?
Se ho capito bene l’osservatore C’ vede dopo un tot di tempo i due gemelli con la stessa età (come è ovvio che sia), ma colui che si trova in C vede prima quello posto in A’ e dopo quello posto in B’, perché la luce da B’ parte dopo e comunque bisogna considerare anche il tempo di propagazione della luce.
Ma se potesse vedere i due gemelli istantaneamente (come se la propagazione della luce fosse istantanea) vedrebbe in un dato istante i gemelli avere età diverse, uno più giovane e uno più vecchio?
Oppure provo a dirlo in un altro modo.
Se gli orologi in A’ e B’ segnano la stessa ora, perché sono sincronizzati, ad esempio le 12, per il sistema fisso quando A’ segna le 12 anche A segna le 12(per esempio), ma quando B’ segna le 12, B invece segna ad esempio le 11.
Ma questo non perché gli orologi di A e B non sono sincronizzati o sballati, ma perché la percezione del tempo di chi si muove rispetto a un asservatore fisso avviene in questo modo.
Ciò che avviene nello stesso istante per un sistema in movimento diventano due istanti diversi per uno fermo. Giusto?
Quindi ribaltando la cosa in un dato istante, un osservatore fermo vede due eventi posti in due posizioni diverse dello spazio in due tempi diversi, quando invece per chi si muove avviene nello stesso tempo?
E’ questo che comporta il concetto della simultaneità?
Spero di non aver abusato troppo della tua pazienza, ma è troppo importante capire questa cosa.
caro Simone,
direi che ci siamo quasi... Ossia, l'ultima parte che hai scritto è praticamente perfetta. Eviterei, invece, la parte dei gemelli, in quanto introduci la frase "C vede B'". Per vedere realmente deve aspettare che la luce di B' arrivi in C e questo è un istante ancora diverso da quelli rappresentati (dovresti prolungare la luce di B' fino a che non incontri C.
In realtà, tutti gli orologi di tutti i sistemi sono perfettamente sincronizzati, ma la simultaneità di un sistema in moto implica la non simultaneità per un sistema fermo (e viceversa, dato che il moto è relativo). La possiamo anche chiamare "apparenza", ma tieni conto che quando il sistema marciapiede effettua delle misure su ciò che capita sul treno deve ammettere che i tempi differiscono e quindi anche la sua realtà lo conferma (caso del muone che arriva veramente a terra). La vera conclusione è che ciò che è simultaneo in un sistema non lo è più per un sistema in movimento inerziale rispetto al primo. Come dici tu, ciò ricade sulla percezione del tempo, dato che il sistema di C deve utilizzare due orologi, mentre quello di C' uno solo.
Dobbiamo sempre ricordare che il diagramma di Minkowski rappresenta, in un sistema che si considera fermo, tutto ciò che capita in altri sistemi. E' un sistema fortemente SOGGETTIVO, ma è la realtà per chi vive su di esso. Le coordinate sono le sue e quindi tutte le linee di simultaneità devono essere inclinate (ossia dare tempi diversi) nel suo.
Sai, il metodo più veloce per trovare la linea di simultaneità è in fondo il primo che avevamo usato... Basta prendere due intervalli di tempo uguali lungo la retta t' (definita dalla velocità del sistema). Tracciare dagli eventi estremi (quello sotto e quello sopra) le due linee della luce a 45° e il punto dove s'incontrano deve essere per definizione sull'asse x', dato che deve essere solidale con il punto di ascissa x' = 0. In pratica è come se su un viaggiatore nella coda di un treno in movimento mandasse un segnale luminoso a un altro situato in un'altra posizione del treno e questo gli rispondesse subito. I tempi di andata e ritorno DEVONO essere uguali dato che la distanza rimane la stessa e la luce viaggia sempre nello stesso modo. Se ciò capita, ossia se le due linee della luce si incontrano in un punto, quel punto deve essere sul treno e deve essere immobile rispetto al primo! In questo modo si costruisce punto a punto tutto il sistema treno, dato che le distanze relative sono sempre le stesse istante per istante, ossia si costruisce proprio l'asse x' spaziale del sistema treno (il treno stesso).
Spero di non averti confuso... ma prova a pensarci e la cosa diventa un nuovo modo ancora per vedere la stessa cosa... Visualizzato questo fatto, prova adesso a pensare se l'operazione di andata e ritorno fosse vista dal marciapiede. La luce impiegherebbe un tempo diverso tra l'andata e il ritorno del segnale di luce tra due punti del treno (se l'andata si accorcia, perché il secondo punto viaggia incontro alla luce, il ritorno si allunga perché la luce deve percorrere uno spazio in più dovuto al movimento del treno). Gira e rigira arriviamo sempre allo stesso punto, ma mentre nel sistema treno i tempi di andata e ritorno vengono presi da un solo orologio, in quello del marciapiede i tempi devono essere presi almeno da due orologi, perché il punto mediano si è spostato spazialmente.
Riflettici e vedrai che con un diagrammino schematico e quasi elementare si può costruire tutta la RR da un punto di vista quantitativo. Geniale, veramente geniale.
Penso che uno dei punti più ostici della rappresentazione sia riuscire sempre a pensare che lo spostamento lungo l'asse t o t' non è un vero spostamento fisico, ma solo temporale, ossia il punto rimane FERMO, mentre descrive infiniti EVENTI.
Comunque, andando avanti con il diagramma, se si hanno le basi, tutto apparirà sempre più chiaro...
Ti ringrazio per l'attenzione e la volontà nel cercare di seguirmi!!! mi ripaga della fatica fatta a cercare di semplificare al massimo concetti che sembrano subito banali ma che poi creano enorme confusione nell'interpretarli veramente a fondo...
mi ripaga della fatica fatta a cercare di semplificare al massimo concetti che sembrano subito banali ma che poi creano enorme confusione nell'interpretarli veramente a fondo...
Ti ringrazio per la tua attenzione.
Spero di non diventare il tuo incubo ricorrente con le mie domande…anche se temo di essere sulla buona strada…
Quando io dicevo “C vede B” nella parte dei gemelli io intendevo istantaneamente.
Provo a spiegarmi.
Se io sono in C nell’istante tA’ della figura 5 e potessi vedere istantaneamente il punto (o l’evento) in A che coincide con A’ e quello in B’ che coincide con B’, come se la luce viaggiasse a velocità infinita, vedrei che gli orologi posti nel mio sistema fisso segnano la stessa ora e quelli posti sul sistema in movimento segnano due tempi diversi?
Di conseguenza se ci fossero due gemelli, vedrei che hanno due età diverse e nel caso specifico quello in B’ essere più giovane?
Ovviamente nella realtà questo non è possibile, perché devo comunque aspettare il tempo che la luce impiega a giungere a me nel punto C, che ovviamente diventa un altro istante.
Spero di essere stato chiaro.
Appena ho tempo penserò alla seconda parte che hai scritto, per adesso ne ho a sufficienza.
scusa Simone... ma faccio un po' fatica a capire la domanda. Provo a dire qualcosa che forse può chiarire le idee...
Se tu sei in C all'istante tA' "vedi" A e B coincidenti con A' e B': sei all'istante in cui il treno passa esattamente davanti al marciapiede. Per accorgerti della non simultaneità deve passare del tempo, ossia la luce di A' e B' deve arrivare in C''. In ogni modo, la simultaneità del marciapiede è sempre verificata per punti come A e B. Non lo è più per punti che si muovono. Quindi, potremmo dire che, per il marciapiede, chi sta in B'1 ed è simultaneo ad A' sembra mandare il segnale prima di suo fratello. Non so, però, se ti ho risposto...
Scusa, ma in questi giorni posso dedicare pochissimo tempo al blog, dato che stiamo sistemando l'alloggio per mia figlia e abbiamo a che fare con idraulici, elettricisti, Enel e cose del genere... Che barba!!! E in più aspettiamo la chiamata dall'ospedale...
Abbiate tutti molta pazienza.... e scusate se a volte non riesco a rispondere con la dovuta accuratezza. Dai... speriamo che si possa ritornare alla normalità tra non molto!!!
Sai Simone,
più che scervellarsi tanto su chi può essere più vecchio o più giovane secondo ipotesi irrealizzabili in pratica, io consiglierei di digerire bene il succo della faccenda. La faccenda sta tutta qui: la retta di simultaneità per un sistema fermo differisce dalla retta di simultaneità per un sistema in movimento e più differisce quanto più il sistema viaggia velocemente. Noi abbiamo solo cercato di dimostralo in vari modi e soprattutto abbiamo cercato di disegnare queste rette. Inoltre, teniamo presente che tutto ciò che vede chi sta fermo è tale e quale a ciò che vede chi sta in moto, dato che la relatività è perfettamente simmetrica. Potevamo ricavare la stessa cosa senza tante parole, ma solo come abbiamo fatto nell'articolo in cui abbiamo trovato gli assi matematicamente sfruttando la trasformazione di Lorentz. Se vogliamo vedere qualche paradosso o qualche caso speciale è meglio utilizzare quelli classici, come quello dei gemelli, dove tanti dubbi se ne andranno via automaticamente. Ancora qualche passetto e ci arriviamo...
In fondo, il povero omino sul marciapiede non può dire altro che i segnali luminosi partiti da A' e B', non possono essere simultanei per i suoi orologi, dato che per potere raggiungere il centro del treno, contemporaneamente, devono partire in tempi diversi (per lui). Lui, in fondo, si accorge solo che la luce di A' lo raggiunge ben prima di arrivare al centro del treno e quindi deve essere partita per prima. (Ciò che vede è il fatto che la luce passa dove è lui, mentre il treno si è già spostato e non può più vedere C"). Da ciò può dedurre che la luce di B' è partita dopo, secondo i suoi orologi. L'evento luce da B' e successivo all'evento luce da A'. Ma, dato che la luce alla fine arriva contemporaneamente in C'', deve ammettere che sono i suoi orologi che non sono sincronizzati. Lui non può, in realtà, vedere C" raggiunto dalla luce, ma solo ciò che gli passa davanti, ossia la luce di A'. Cerchiamo di separare ciò che in realtà si può vedere e ciò che, invece, si può dedurre...
Comunque, tu insisti pure quanto vuoi e cercherò di aiutarti al meglio delle mie possibilità...
Caro Enzo, premetto che al Test non rispondo, sono curioso di vedere le altrui risposte.
Dato che una delle cose della RR che a mio avviso crea confusione è la visione del medesimo fenomeno passando da un sistema di riferimento all’altro, ho realizzato qualche figura in cui i due fenomeni (lampade sul treno oppure lampade sul marciapiede) vengono visti sia dal treno sia dal marciapiede.
Le figure, sempre che siano corrette , mostrano graficamente anche la perfetta simmetria di queste due visioni… in cui, a turno, ognuno ritiene di esser fermo (sul marciapiede o sul treno)!
, mostrano graficamente anche la perfetta simmetria di queste due visioni… in cui, a turno, ognuno ritiene di esser fermo (sul marciapiede o sul treno)!
http://www.astrobin.com/full/34211/J/?real=&mod=
Paolo
Beh... Paolo, a te piace vincere facile... Dai divertiti pure e restiamo in attesa di aumentare il numero dei "ben preparati" al passo successivo!
 Bravo, come sempre!
Bravo, come sempre!
Anzi Paolo... ti chiederei di aiutarmi (ormai sei in grado di farlo e magari vedi le cose da un punto di vista diverso...): ti chiederei di leggere anche l'ultimo post ultra semplificato (3bis(1)) e guarda se secondo te manca qualcosa per renderlo ancora più comprensibile. Un lavoro di "equipe" ci porterà a scrivere qualcosa di veramente utile per tutti e nettamente differente da quello che si trova in tante pagine web... Alla fine, estrarremo da tanti articoli il succo veramente importante... Insomma, costruiamoci la nostra RR un po' alla volta e tutti assieme! Poi, magari, la manderemo a Einstein per una sua approvazione

Meglio lavorare così che esasperare le domande prima che gli argomenti siano stati affrontati (cosa che capita nei normali forum...).
Grazie per la collaborazione!!!!
Ti ringrazio per la tua perseveranza nel continuare a spiegarmi, mi rendo conto che sono un po’ un peso…
Ogni tua osservazione, per me è un nuovo punto di vista sul quale riflettere e capire meglio.
Comunque credo di aver capito abbastanza bene il concetto di simultaneità, o al limite se così non è ho preso una grossa cantonata.
Il mio problema forse è che non riesco a spiegarmi in modo rigoroso, uso troppo spesso termini come “vedere…” “vedere se…” ecc., quando magari non è possibile farlo realmente.
Il fatto è che io cerco sempre di andare un po’ oltre, immaginando certe situazioni magari irrealizzabili, per darmi un riscontro, diciamo, un po’ più pratico e alla mano... purtroppo sono fatto così.
Comunque, per capire se sono sulla strada corretta provo a spiegarti con mie parole quello che ho compreso sulla simultaneità, cercando di essere il più conciso possibile e senza estrapolazioni varie.
Stabiliamo che gli orologi in ciascun sistema di riferimento siano tra loro sincronizzati e che C sia il punto mediano tra A e B, e C’ il punto di mezzo tra A’ e B’.
Stabiliamo anche che nell’istante tA’ A coincide spazialmente con A’, B con B’ e C con C’.
Se nel medesimo istante vengono accese simultaneamente due lampadine poste in A’ e B’ (sistema in movimento) si ha quanto segue.
Dopo un certo tempo i due raggi di luce arrivano simultaneamente in C’, il quale, dato che si trova nel mezzo tra A’ e B’, stabilisce a maggior ragione che le due luci sono partite per lui nello stesso instante, ovvero che gli orologi posti in A’ e B’ segnano la stessa ora.
La stessa cosa deve avvenire anche per il sistema fermo, quindi per C le luci si incontrano in C’ dopo un certo tempo, ma in questo intervallo di tempo C’ si è spostato e quindi non coincide più con C.
Si deduce che la luce partita da A’ passa per C prima di quella proveniente da B’.
Ma dato che la velocità della luce è uguale in tutti i sistemi di riferimento, ovvero è indipendente dal sistema di riferimento, e che anche C si trovava al momento delle accensioni delle lampadine nel centro tra A e B ovvero tra A’ e B’, per ipotesi, in teoria le due luci si sarebbero dovute incontrare anche in C.
Ma questo non può avvenire, perché dopo un certo tempo si incontrano in C’ che intanto si è spostato e non coincide più con C.
Per giustificare quanto avviene si può solo pensare che per il sistema fermo la luce da B’ sia partita dopo rispetto a quella partita da A’, ovvero le due luci non sono partite simultaneamente ma in due istanti diversi.
Al momento dell’accensione delle due lampadine gli orologi posti in A e B non sono sincronizzati, ovvero segnano due tempi diversi, quando invece gli orologi di A’ e B’ segnano lo stesso tempo.
Per il sistema fermo la luce parte da A’ nell’istante tA’ e da B’ nell’istante tB’1.
Se l’orologio posto in A’ è sincronizzato con B’ e quello in A è sincronizzato con B, se poniamo che A segna lo stesso tempo di A’ otteniamo che l’orologio di B non segna lo stesso tempo di B’.
Quindi due eventi che nel sistema in movimento avvengono nello stesso istante, per il sistema fermo diventano due eventi che avvengono in due istanti diversi.
La retta che congiunge i punti A=A’ con B’1 diventa il luogo geometrico dei punti o eventi che sono simultanei per il sistema in movimento rappresentato rispetto al sistema fermo.
Ecco, quanto sopra è quello che ho capito.
Se non è così, provo a rifletterci sopra meglio.
perfetto Simone!
Volevo puntualizzare che la continua ricerca di semplificazione non era diretta a te in particolare. Ci mancherebbe... Tu, anzi, hai il merito di chiedere ed esprimere dubbi. Oltretutto avevi già capito abbastanza bene prima... Tuttavia, ciò che tu esprimevi mi ha aiutato a "vedere" punti che potevano essere critici per molti altri che non se la sentivano di mettersi in mostra.

Mi rendo perfettamente conto che la RR è una di quelle cose che sembrano piuttosto elementari, ma che poi ti creano immediatamente confusione e riuscire a evidenziarne i punti critici, che prima o poi escono allo scoperto, è essenziale. L'idea di vedere e misurare, in uno spaziotempo dove non puoi mettere gli oggetti, ma solo gli eventi è facile solo a parole, ma non con i fatti. Il pensare che ciò che si muove in verticale e poi anche in obliquo sia sempre lo stesso punto che si trasforma in infiniti eventi è sicuramente un concetto lontano dalla realtà. Bisogna sempre stare bene attenti a non mischiare ciò che facciamo nelle due coordinate spaziali con quello che si rappresenta nelle due coordinate spaziotemporali. Soprattutto dopo che si siamo accorti che il piano della figura non è più euclideo...
Anche se nessuno commenta, spero tanto che questi ulteriori approfondimenti servano ad aprire finestre sempre più ampie. Posso solo dirti che tu mi hai aiutato molto a capire dove intervenire! Se poi sono approfondimenti inutili per la maggioranza, pazienza... prendeteli come ripassi...
Meglio abbondare...
Caro Enzo credo che hai fatto il massimo per rendere comprensibile il concetto evidenziando negli articoli l'approccio mentale per la comprensione della simultaneità ora non ci resta in futuro quando si presenteranno dubbi andarci a rileggere questi articoli con calma e da queste basi cercar di comprendere le parti più complesse della relatività speciale che in futuro andremo ad affrontare.
grazie Foscoul,
comunque, come hai visto, ho anche inserito un esperimento diverso (che concluderò domani o dopodomani) che arriva sempre allo stesso punto (3bis 1 e 2). Poi ditemi quello che preferite...
Caro Enzo, sono felice di averti aiutato in un qualche modo…
Comunque sono concorde con te nel dire che è meglio abbondare.
Provo a rispondere alla domanda finale (senza avere letto i commenti precedenti):
l'osservatore sul treno vedrà accendersi prima la lampadina posta in B, la cui luce dovrà percorrere, per raggiungerlo, uno spazio inferiore rientro a quello della luce partita da A.
Immagino che il relativo diagramma di Minkowski dovrebbe essere quello della figura 6 simmetrico rispetto all'asse t, perché la velocità apparente del marciapiede rispetto a quella del treno (v) sarà -v.
Se, per assurdo (visto che il treno, per quanto piccolo possiamo pensarlo, non sarà mai ipotizzabile privo di massa), il treno si muovesse a velocità uguale a quella della luce, l'osservatore su di esso non vedrebbe mai accendersi la luce posta A. Giusto?
cara Daniela,
la prima parte è giusta. Sulla seconda direi che più che non vedere la luce accendersi deve aspettare un tempo infinito perché raggiunga il punto di mezzo... ma solo perché il sistema si muove solidalmente con la luce. La simultaneità con B si raggiunge all'infinito. Ti consiglio di arrivare alla conclusione stringendo sempre di più il sistema in movimento e vedrai che tutto rimane uguale, ma è solo il tempo che si dilata, degenerando in un orologio che non si muove. La luce deve viaggiare sempre nello stesso modo, dato che la sua velocità non dipende dal sistema di riferimento. Il fotone corre e come! E' il suo orologio che sembra fermo.
Ok, grazie!
Scusa Daniela,
ma ieri sera ero un po' di corsa... cerco di spiegarmi meglio.
Devi tener conto che la luce viaggia sempre alla stessa velocità qualsiasi sia il sistema di riferimento. Cosa capita, allora, all'interno del treno? Lui si sente fermo (ed è del tutto equivalente a un sistema fermo), per cui niente può cambiare, qualsiasi sia la sua velocità. Teniamo conto che noi stabiliamo una sua velocità solo in base a un altro sistema. La velocità non è una proprietà del sistema in movimento e non può assolutamente modificare ciò che capita al suo interno. Quindi, gli osservatori solidali con il sistema in movimento vedono la luce partire dai due estremi e giungere al centro. La luce ha sempre velocità c, mentre tutto il resto è fermo. Questo capita anche se il sistema è visto muovere a velocità c da un altro sistema. Al treno non interessa assolutamente niente e lui rappresenta il solito triangolo isoscele.
Per chi è esterno, la luce continua a viaggiare a 45° e viene vista tale e quale a prima. Quello che cambia è che anche il treno schizza via alla stessa velocità. Il suo orologio non si muove e tutto tende a infinito. Ne consegue che anche la linea di simultaneità diventa proprio la traiettoria della luce. La figura teoricamente non cambia, ma bisognerebbe andare fino all'infinito, dove tutto capita insieme....
Forse, per una comprensione ancora migliore, potresti leggere -appena puoi- l'ultimo che ho scritto (in evidenza) sulla preparazione del paradosso dei gemelli...
Grazie per sollevare i tuoi dubbi! Dobbiamo risolverli all'inizio!!!!
Grazie di nuovo!
Ma ti confesso che anche la prima risposta mi sembrava esauriente e non avevo intuito che l'avessi scritta di corsa!!
Come ti avevo accennato, in questi giorni (forse per merito dell0 iodio che respiro mentre leggo in spiaggia :-P), sto recuperando un po' di terreno: ho finito di leggere la parte generale e i primi tre approfondimenti RRR; tra poco avrei intenzione di iniziare i tre articoli sul diagramma di Minkowski, ma credo che prima, visto che mi hai incuriosito, darò un'occhiata alla preparazione del paradosso dei gemelli
scusami Dany se ho esagerato...
Ma, sai, preferisco sempre abbondare e poi... non tutti respirano lo iodio!!!
"Melius est abundare quam deficere"... E' sempre un piacere leggere le tue abbondanti spiegazioni!!

E ora, dopo avere letto, gli ultimi articoli (compreso quello ispirato dalla sottoscritta, nel quale hai fatto bene a ricordarmi che il sistema che si considera fermo deve essere costituito da infiniti osservatori ognuno con il proprio orologio...meno male che hai abbondato!), spengo il pc e vado a IODIZZARMI!!!
Dopo varie peripezie ho partorito questo grafico:
http://www.astrobin.com/full/204573/0/
dal quale si evince che l'osservatore C' riceverà la luce prima da B e poi da A.
Pensavo fosse giusto ma poi ho controllato il grafico che aveva fatto Paolo ed ho visto che nel suo sistema i due assi sono nel 4° quadrante... ho sbagliato?
caro SMA,
il quadrante dipende da come hai scelto la velocità... o positiva o negativa... Se ho capito bene...
Ciao Enzo, la mia velocità è -v... hai visto il grafico?
appunto SMA... e quindi la figura si ribalta.
Si anche la mia è ribaltata... quindi è giusto?
sì, sì. volevo solo dire che cambiando la direzione cambia il quadrante...
scusa SMA...
ero un po' di fretta e non ricordavo più che c'era una domanda precisa nel testo... e ho fatto confusione...
Dunque, nel tuo grafico hai chiamato A' sia il punto del sistema nero che quello del sistema rosso. O almeno non ho capito bene il grafico. Il succo è semplice, la luce deve partire dai due punti A e B del sistema nero che si (se immagini A'B' rosso fermo) muove verso sinistra, con velocità - v. Per il sistema rosso è quindi la luce partita da B che arriva prima in C', ossia nel punto di mezzo del sistema che si considera fermo.
Ciao Enzo,
il grafico si riferiva al tuo test nell'articolo:
"Immaginate di mettere le due lampadine sul marciapiede, in A e B, e di farle accendere simultaneamente in quel sistema. Disegnate il grafico di prima (ossia determinate la simultaneità) ponendo come sistema di riferimento fisso quello del treno"
Effettivamente ho usato le stesse lettere A' e B'... quelle nere indicano i punti sul treno, mentre A',B' e C' in rosso indicano gli eventi sul sistema marciapiede al tempo t'.
OK SMA!
Scusa SMA, ho visto che hai citato le figure che avevo costruito, però mi sembra che il problema del quadrante non esiste.
In sintesi nella mia figura B' coincide con l'origine degli assi, nella tua è A' che coincide con l'origine degli assi..... per cui cambia solo la posizione iniziale del sistema treno fermo/marciapiede e di conseguenza per te il grafico risulterà a cavallo tra il 1° e il 4° quadrante, nella mia figura risulta interamente nel 4° quadrante....
Abbiamo solo posto i due segmenti iniziali in posizione differenti rispetto all'origine degli assi.
Ciò che invece a mio avviso rischia di creare equivoci è che il segmento rosso che dopo un certo tempo è stato indicato come A'; C'; B'.
Forse il problema è solo convenzionale, ma rischia di creare confusione.
Il sistema scelto come riferimento è quello del treno e nel grafico hai indicato come assi t' e x', per cui ci si aspetta che i “punti” solidali con questo sistema siano indicati come A', B' e C'.
Visti dal treno, A', B' e C' (ossia il treno), si muovono solo nel tempo e non nello spazio.
Visti dal treno sono A, B e C (ossia il marciapiede) che si muovono anche nello spazio oltre che nel tempo.
Penso che ora sia chiaro l'equivoco, per cui se nella tua figura il treno è rappresentato dai punti A; B e C si tratta solo di un problema convenzionale, se invece il treno è rappresentato da A'; B' e C', il grafico non è corretto, poiché visto dal treno, quest'ultimo si deve muovere solo nel tempo.
Spero di non aver detto qualche sciocchezza, ma in tal caso urge un intervento di Enzo.
Paolo
E' giusto quello che dice Paolo, ma penso che SMA intendesse proprio quello nel suo grafico. Anch'io avrei preferito veder viaggiare ABC, ma l'importante è capire il concetto...
Insomma, basta rifare la figura del testo, cambiando v in - v e niente cambia....
Tutti d'accordo? Se no riprendiamo la questione...
@Paolo:

Grazie per la risposta, infatti mi interessava sapere se il grafico era corretto e questa è affermativa, visto che la differenza era solo nel "posizionamento" del marciapiede, ma volevo essere sicuro di questo.
Ho fatto un pò di confusione con A'C'B', non sapevo come nominarli e mi sono salvato in calcio d'angolo scrivendoli in rosso
Comunque dai per essere la prima prova con la RR e Photoshop è andata abbastanza bene...
Direi che andata benone
Paolo
Soffermandomi sulla figura 4 noto che anche col treno in corsa le lampadine si accendono quando sono equidistanti da C. In considerazione allora del secondo postulato sulla TRR, mi viene da pensare che la luce di queste dovrebbe raggiungere contemporaneamente quel punto. Perciò sarei giunto a questa conclusione. Il passeggero si vede raggiunto dalla luce delle due lampadine contemporaneamente e vede l’amico sul marciapiede raggiunto in tempi diversi. Questo suo amico sul marciapiede si vede raggiunto dalla luce contemporaneamente e vede l’amico sul treno raggiunto in tempi diversi. Ho però paura di sbagliare e chiedo cortesemente a Lei il suo parere.
Grazie.
hai detto benissimo Gian Carlo: la simultaneità è relativa al sistema di riferimento e la differenza aumenta coil crescere della velocità relativa.
Io ti consiglierei, però, di andare direttamente sull'articolo della RR che trovi nell'archivio. Lì sono stati messi assieme tutti i vari articoli isolati con qualche aggiunta che potrebbe venire utile...
http://www.infinitoteatrodelcosmo.it/2015/04/08/le-basi-della-relativita-ristretta-o-speciale/
ciao e... sempre a disposizione!
ciao vincenzo,
ti ringrazio perché mi hai chiarito molti dubbi. nonostante abbia studiato relatività diverse volte, dopo un po' di tempo mi dimentico i dettagli e devo tornare a studiare.
in particolare, mi sono chiarito l'esempio dell'osservatore sul treno in movimento e quello sul marciapiede, in cui le accensioni delle lampadine non possono essere eventi simultanei per entrambi. vorrei solo far notare che, secondo me, sarebbe più chiaro se considerassimo un osservatore sul marciapiede che si trova non esattamente a metà tra A e B, ma un po' più spostato, esattamente nel punto in cui si troverà C' quando questo riceverà contemporaneamente i due segnali lumonosi (in figura 5, al posto di C, il punto sull'asse x esattamente sotto C''). Dico questo perché così si mostra bene che nonostante i due osservatori si trovino nello stesso istante di tempo e nello stesso punto dello spazio, ricevono due segnali che sono simultanei solamente per uno dei due osservatori.
Ovviamente, di fatto sono lo stesso sistema di riferimento (solo una traslazione spaziale), ma penso che questo chiarisca meglio il significato dell'esempio, almeno dal mio punto di vista.
giovanni