Questo articolo fa parte della serie "Disegnare in tre dimensioni: tra storia e pratica"

 

E' tanto che avrei voluto parlare di prospettiva e di altre due tecniche di descrizione di ciò che realmente vede l'occhio e della sua rappresentazione su un piano. Questo è un nostro limite... dato che ciò che vediamo viene sempre proiettato su un piano. Il problema quindi si riduce a una rappresentazione bidimensionale della realtà tridimensionale in cui viviamo. Se aggiungiamo la mia passione per l'arte si comprende questa  esigenza. Sarà, però, un approccio del tutto personale che, quindi, potrebbe anche essere perfezionato nel tempo, magari quando vi sarà un ritorno dalle ferie di moltissimi lettori.  Insomma, partirò per "istinto" e poi, grazie anche ai vostri commenti, cercherò di essere più rigoroso.

Introduzione

Disegnare ciò che si vede realmente: questo è il problema. Per disegnare, però, bisogna prima capire ciò che l'occhio ci mostra. Noi viviamo in un mondo tridimensionale (parlando di spazio, ovviamente) ma vediamo tutto proiettato su un piano.

La vista umana pone problemi non facili al disegno nelle tre dimensioni. La faccenda non è molto diversa da ciò che si vede nel cielo: tutte le stelle, i pianeti e le galassie vengono proiettate su una superficie sferica, senza alcun aiuto visivo per prendere coscienza delle loro distanze. In una zona limitata della sfera celeste possiamo facilmente sostituire la sfera con un piano e concludere che siamo obbligati a vedere solo in due dimensioni, da cui la nascita delle costellazioni e di gran parte dell'astrologia che ancora permea quel poco che è rimasto del pensiero umano.

Anche nell'ambiente che ci circonda, tutto ciò che vediamo si proietta su un piano, ma, fortunatamente, ci sono alcune caratteristiche di questa proiezione che seguono regole ben precise. Un problema che ha sempre coinvolto le civiltà e che ha portato a soluzioni più o meno rigorose,  soprattutto ai tempi degli antichi greci e romani.

Immaginiamo che io sia un "architetto"  e debba portare il progetto di un edificio a forma di parallelepipedo a chi mi ha chiesto di costruirglielo. La cosa più facile è quella di riportare le dimensioni dell'edificio sulle tre proiezioni  che si vedono ponendosi di fronte ai due lati e dall'alto (a e b sono le dimensioni del rettangolo di base e h l'altezza).   Considerando un sistema di coordinate x,y,z le tre proiezioni sono quelle in cui si considerano  come linee di vista l'asse x, l'asse y e l'asse z (Fig. 1) .

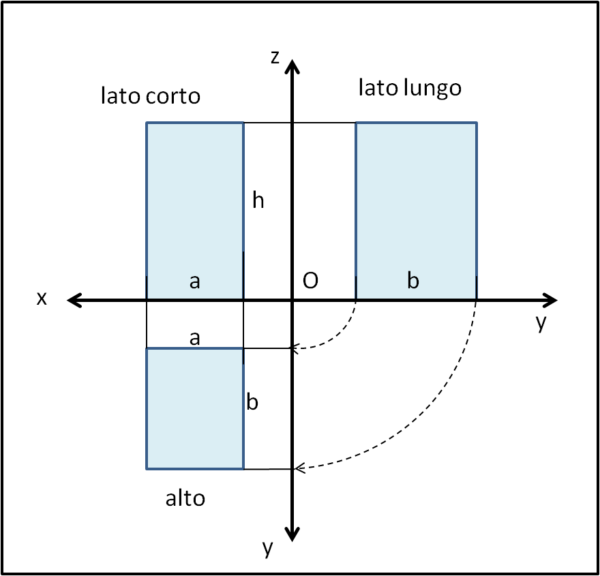
Tutto segue perfettamente la realtà visuale a due dimensioni. Ma l'armonia delle proporzioni (di cui sicuramente erano padroni già gli egiziani e ancora di più i greci che della geometria avevano fatto una vera arte e un culto quasi soprannaturale) su ogni singolo piano, come apparirà quando il monumento sarà costruito e si potrà vedere da varie angolazioni?  In altre parole, quale sarà la resa visuale definitiva tenendo conto che la vista "schiaccia" tutto, sempre e comunque, nelle due dimensioni?

Il punto chiave di tutto ciò è la presa di coscienza che esiste un punto all'infinito comune a tutte le rette parallele tra loro. Il famoso punto improprio che abbiamo usato per iniziare il nostro corso di matematica. Non solo un punto, però, ma un'intera retta impropria o all'infinito, tale da contenere TUTTI i punti all'infinito. Un concetto questo che è ben lontano dall'idea che due rette parallele non si incontrano mai. A questo punto, varrebbe la pena ripercorrere la storia della prospettiva attraverso i secoli e come essa sia stata affrontata dalle varie civiltà. Un discorso molto lungo e articolato che prima o poi affronteremo.

Possiamo sicuramente dire che i greci avevano compreso gran parte del funzionamento dell'occhio umano e sicuramente sapevano prevedere e disegnare gli "scorci", ossia le immagini distorte che la visione bidimensionale è costretta a imporci.  Non di meno dovevano esserne padroni i romani.

Ma pensiamo anche al lungo periodo medievale in cui le rappresentazioni parietali si riferivano quasi sempre a immagini sacre,  che dovevano trascendere la forma tridimensionale. Si preferiva escludere del tutto la visione spaziale per rimanere in una visione puramente bidimensionale, presa a simbolo stesso dell'immaterialità, dell'apparenza divina del tutto al di fuori del mondo in cui viveva l'uomo.

Un sotterfugio perché non si era più capaci di seguire certe regole che i romani, popolo sacrilego, aveva quasi sicuramente descritto? In qualche modo un ritorno forzato o voluto alle figure egiziane viste sempre di profilo? O veramente un obbligo interiore? I primi accenni di spazio si hanno con la nascita del chiaroscuro (Cimabue) e poi con le prime ambientazioni di Giotto dentro a edifici  o con edifici di scorcio.

Proprio in Giotto, la tecnica appare ancora rudimentale, ma la rivoluzione ormai è in atto. Il fatto stesso che l'uomo o la divinità occupi uno spazio non può che sfociare nel rinascimento e nell'attenta analisi dei reperti delle civiltà più antiche. In poche parole nasce la prospettiva!

La prospettiva

Una conquista, questa, che è stata affrontata e descritta in modo perfetto nel 1400, grazie a giganti come Brunelleschi, Masaccio, Donatello e portata al livello di rigorose argomentazioni soprattutto da Piero della Francesca e da Leon Battista Alberti. Con Leonardo, soprattutto, nasce anche la prospettiva aerea, ossia la capacità di disegnare e interpretare lo spazio anche senza bisogno di strutture geometriche, ma affidandosi alle proporzioni e alle sfumature di colore.

Tra parentesi, proprio il passaggio da Giotto a Masaccio ha stimolato il racconto che abbiamo giustamente riproposto come premessa a questo e a quelli che seguiranno.

Rientriamo nel campo più tecnico e dedichiamoci, allora, a una descrizione estremamente semplificata, ma più che sufficiente, delle regole da seguire per riuscire a riprodurre al meglio ciò che la vista ci impone. Poi vedremo anche come i grandi artisti abbiano saputo giocare con queste regole per ottenere effetti particolarmente impressionanti e scenografici o, addirittura, a progettare piazze, edifici e quant'altro in modo che apparissero, alla vista, diversi dalla loro forma reale. Una vera e propria sorta di illusionismo!

Prospettiva centrale

Come già si è detto, il punto chiave nella visione prospettica è che le rette parallele si incontrano sempre in un punto. Poniamoci nelle condizioni più semplici, ossia guardiamo una figura geometrica, ad esempio un rettangolo, in posizione ortogonale a un suo lato. Non mi picchiate, ma sceglierò un metodo di descrizione che sembrerà più complicato di quello che sia realmente. Tuttavia, se facessi una figura a tre dimensioni per illustrarvelo, userei, almeno parzialmente, proprio quello che voglio mostrare. insomma un serpente (bisciabova?) che si morde la coda. Ne segue che andrò avanti attraverso figure piane e solo alla fine, per riassumere i concetti, vedremo una rappresentazione tridimensionale.

La Fig. 2. rappresenta il piano di terra (pt). Su di lui segno la posizione (proiettata su questo piano) di chi guarda (il suo occhio sia O) e disegno il  rettangolo ABCD.

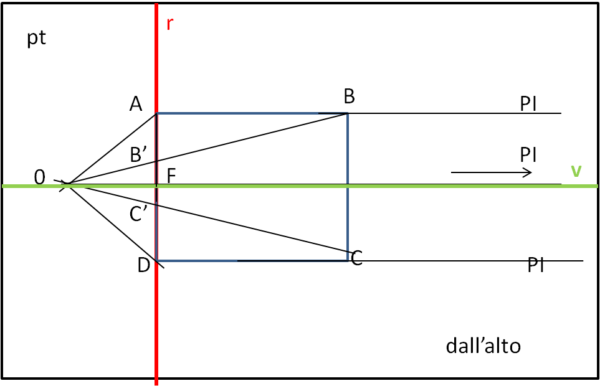
Inoltre pongo come linea di rappresentazione r proprio quella che prolunga il lato minore del rettangolo. Il piano passante per r e perpendicolare a pt sarà identificato come piano di rappresentazione (pr) e sarà quello dove nascerà la nostra visione prospettica. Il piano passante per v (linea di vista) e perpendicolare a pt (e quindi anche a pr) lo chiamiamo piano di vista (pv). Notiamo bene che la linea di vista è stata scelta perpendicolare al lato minore AD del rettangolo e, inoltre, essa divide  proprio a metà il segmento AD. Questa figura la possiamo chiamare visione dall'alto e ci dà quasi tutte le informazioni necessarie.

Notiamo subito una fatto fondamentale: tutte le rette come AB e DC raggiungono lo stesso punto all'infinito. Tuttavia questo punto deve essere riportato sul piano su cui voglio eseguire il disegno finale, ossia sul piano pr che è perpendicolare alla  linea di vista.

Per visualizzare meglio la faccenda portiamoci sul piano che contiene la linea di vista v ed è perpendicolare al piano di terra, ossia su pv. Abbiamo la Fig. 3.

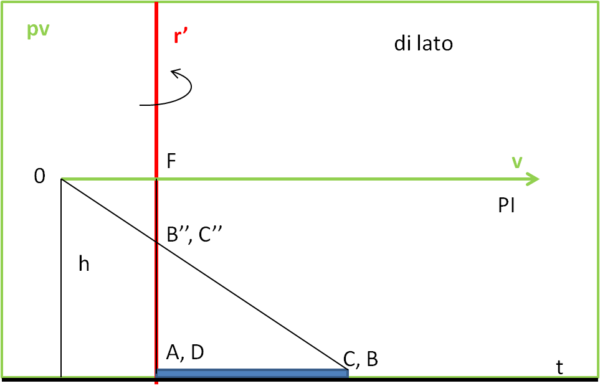
L'occhio O sarà situato a una certa altezza h rispetto al piano di terra e il punto in cui devono confluire le rette parallele ad AB e CD, ossia F, deve stare sulla perpendicolare alla linea di vista. Questo è quello che capita nella visione apparente, ma nel disegno potrei anche spostarlo in alto o in basso (vedremo dopo cosa succederebbe). Chiamiamo questa figura visione laterale.

Come vediamo, la Fig. 3 non è strettamente necessaria per la costruzione finale, tuttavia ci serve per capire meglio la situazione. Sulla linea di terra t riportiamo il rettangolo che sarà visto come un segmento. Non facciamoci, però, ingannare: A e D sono due punti ben separati (lato corto del rettangolo), che stanno sulla linea r, di rappresentazione. La retta r' rappresenta, in questa figura, la traccia del piano di rappresentazione  pr sul piano della Fig. 3. Su questo stesso piano deve stare anche il punto F. Ne segue che AFD  identifica un triangolo isoscele su questo piano (abbiamo preso, infatti, OF come asse del lato minore AD, vedi anche Fig. 2). Il punto F non è altro che il punto all'infinito delle rette AB e CD, identificato sul piano di rappresentazione.

Non ci resta che visualizzarlo in Fig. 4, dopo aver ruotato di 90° la Fig. 3 attorno a r'. In altre parole ci portiamo nel piano di rappresentazione dove deve comparire ciò che vediamo realmente (t' è la linea di terra in questa configurazione).

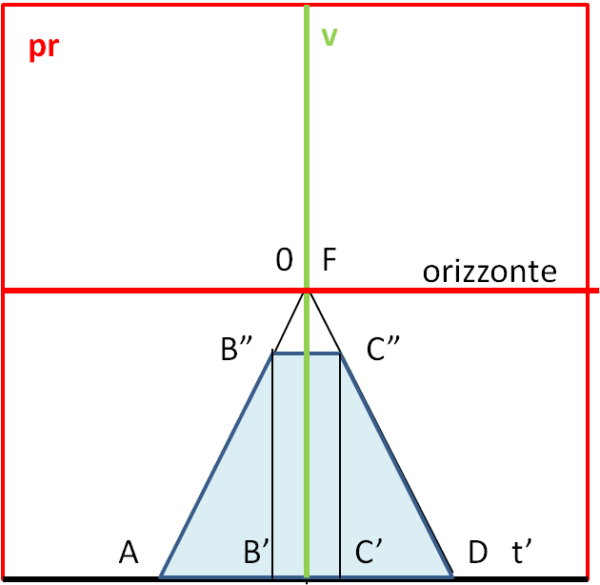
Il lato AD, per come è stata scelta la retta r di Fig. 2, resta identico a se stesso, ma la stessa cosa non capita per i vertici B e C.  Il piano di rappresentazione deve contenere il nostro rettangolo "deformato" a causa del non parallelismo apparente delle rette AB e CD. Le due linee AB e DC si devono incontrare nel punto F, il punto all'infinito che sta sul prolungamento della linea di vista, proiettato sul piano di rappresentazione.  Il punto F lo chiamiamo punto di fuga. La retta passante per F e parallela a t' viene chiamata linea dell'orizzonte. Il suo significato è chiaro, dato che contiene il punto all'infinito F (una retta che sarà molti importante per la visione finale).

Per disegnare i punti B e C "apparenti", teniamo conto che essi devono stare nel piano di rappresentazione, ma anche lungo le congiungenti A e D con F. Questi due punti (B', C') si determinano subito con la Fig. 2, tracciando le rette che vanno da B e C all'occhio O (ciò è quello che capita in realtà e che dobbiamo seguire). In questo modo, individuati B' e C' sulla retta t' (che è anche una r), non ci resta che tracciare le perpendicolari da questi punti alla retta t' fino a incontrare il triangolo AFD in B" e C" (Fig. 3). L'apparenza visiva del rettangolo ABCD sarà data da ABC''D''. Il piano di rappresentazione, che è quello della Fig. 4, possiamo anche chiamarlo visione frontale, ossia proprio quella che appare al nostro occhio.

Per ricapitolare ciò che è sembrato, forse, eccessivamente complicato e sovrabbondante, possiamo ora permetterci di raffigurare ciò che abbiamo fatto attraverso una figura a tre dimensioni (eseguita con un'altra tecnica di cui parleremo in seguito). Una visione questa che non disturba e non confonde più di tanto solo perché abbiamo ormai imparato a comprenderla immediatamente, ma cerchiamo di pensare alla difficoltà che comportava quando ancora non si era capito come si vedesse qualcosa e come lo si potesse raffigurare.

La Fig. 5 parla da sola, avendo mantenuto i colori dei tre piani fondamentali e le lettere usate precedentemente.

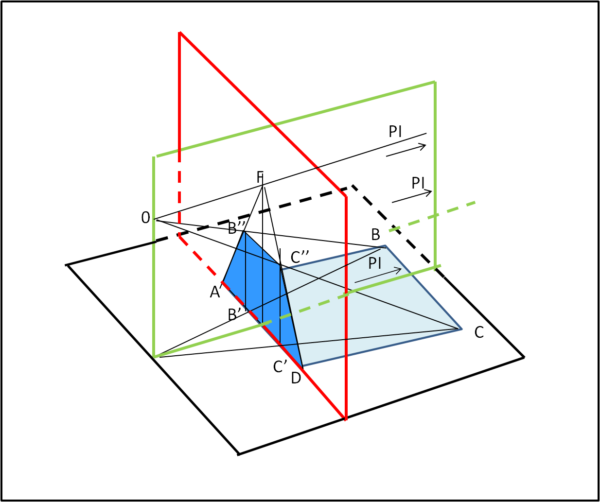
Abbiamo imparato che la Fig.2 ci dà, in questo caso, tutti i dati necessari. Le cose cambieranno di poco passando da una figura piana a una figura solida. Continuiamo, comunque, a rimanere con una figura piana, variando un poco le condizioni iniziali.

Alla prossima...